ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.04.2021
Просмотров: 416
Скачиваний: 1
21
Пример
5.
2
1
3
2
5
x
y
x
×
=
.
1).
1
2
ln
ln 5 2 ln
3 ln
y
x
x
=
+ ×
- ×
.
2).
( )
( )
1
1
2
2
ln
ln
2
3
;
y
y
x
x
x
x
¶
¶
=
= -
¶
¶
.
3).
2
2
2
2
1
2
1
2
1
2
2
3
4
9
y
x
x
E
x
x
E
E
x
x
æ
ö
æ
ö
=
× D
+
× D
=
×
+ ×
ç
÷
ç
÷
è
ø
è
ø
.
По
известной
относительной
погрешности
с
помощью
формулы
(6.4)
можно
рассчитать
значения
абсолютных
погрешностей
:
y
y y E
D = ×
.
В
таблице
6.1
приведены
примеры
формул
результирующих
абсо
-
лютных
и
относительных
погрешностей
косвенных
измерений
.
Таблица
6.1
Функция
Абсолютная
погрешность
Относительная
погрешность
1
2
3
x
x
x
+
+
( ) ( ) ( )
2
2
2
1
2
3
x
x
x
D
+ D
+ D
( ) (
) ( )
2
2
2
1
2
3
1
2
3
x
x
x
x
x
x
D
+ D
+ D
+
+
1
2
x
x
-
( ) ( )
2
2
1
2
x
x
D
+ D
( ) ( )
2
2
1
2
1
2
x
x
x
x
D
+ D
-
1
2
x x
×
(
) (
)
2
2
1
2
2
1
x
x
x
x
× D
+
× D
2
2
1
2
1
2
x
x
x
x
æ
ö
æ
ö
D
D
+
ç
÷
ç
÷
è
ø
è
ø
1
2
ln
x
x
2
2
1
2
1
2
x
x
x
x
æ
ö
æ
ö
D
D
+
ç
÷
ç
÷
è
ø
è
ø
2
2
1
2
1
1
2
2
1
ln
x
x
x
x
x
x
æ
ö
æ
ö
D
D
×
+
ç
÷
ç
÷
è
ø
è
ø
C
x
1
C
C x
x
-
×
× D
x
C
x
D
×
C
x
1
1
1
C
x
x
C
-
×
× D
1
x
C x
D
×
sin
x
cos
x
x
× D
ctg x
x
× D
cos
x
sin
x
x
× D
tg x
x
× D
tg x
2
cos
x
x
D
2
sin 2
x
x
× D
ctg x
2
sin
x
x
D
2
cos 2
x
x
× D
arctg x
2
1
x
x
D
+
(
)
2
1
x
arctg x
x
D
×
+
22
7.
Грубые
погрешности
Грубой
называют
погрешность
,
существенно
превышающую
ожи
-
даемую
при
данных
условиях
эксперимента
.
Причинами
грубых
погрешностей
могут
быть
внезапные
и
кратко
-
временные
изменения
условий
эксперимента
или
оставшиеся
незамечен
-
ными
неисправности
аппаратуры
.
Грубые
погрешности
могут
сильно
иска
-
зить
среднее
значение
,
среднее
квадратичное
отклонение
и
доверительный
интервал
.
Поэтому
измерения
,
содержащие
грубую
погрешность
,
обяза
-
тельно
исключают
из
серии
результатов
измерений
.
Обычно
грубые
погрешности
сразу
видны
в
серии
полученных
ре
-
зультатов
,
но
в
каждом
конкретном
случае
наличие
грубой
погрешности
необходимо
доказать
.
Существует
ряд
приёмов
и
формул
для
выявления
результатов
,
содержащих
грубую
погрешность
.
Выбор
критерия
зависит
от
числа
измерений
.
В
случае
относительно
большого
числа
измерений
(
)
20
n
³
исполь
-
зуют
критерий
3
s
.
В
этом
случае
сомнительный
результат
i
x
i -
го
изме
-
рения
отбрасывают
,
если
3
i
x x
s
-
>
.
Величины
x
и
s
вычисляют
без
учёта
результата
i
x
,
являющегося
сомнительным
.
При
относительно
небольшом
числе
измерений
(
)
10
20
n
< <
исполь
-
зуют
критерий
Романовского
,
основанный
на
распределении
Стьюдента
.
При
использовании
критерия
Романовского
с
помощью
формулы
(3.16)
рассчитывают
СЛ
x
D
.
Если
выполняется
условие
i
СЛ
x
x
x
- > D
,
где
i
x
–
ре
-
зультат
,
вызывающий
сомнение
,
то
погрешность
является
грубой
и
резуль
-
тат
i
x
не
учитывают
.
Если
число
измерений
невелико
(
)
10
n
£
,
то
для
выявления
грубой
погрешности
можно
использовать
критерий
Шовине
.
Согласно
этому
кри
-
терию
промахом
считается
результат
i
x
-
го
i
измерения
,
если
разность
i
x x
-
превышает
значение
k
s
×
,
где
коэффициент
k
зависит
от
числа
из
-
мерений
:
2,0;
8
10;
1,9;
6
8;
1,7;
3
6;
1,6;
3.
если
n
если
n
k
если
n
если
n
< £
ì
ï
< £
ï
= í
< £
ï
ï
=
î
8.
Запись
результатов
.
Правила
округления
При
выполнении
вычислений
с
приближёнными
числами
необходи
-
мо
учитывать
следующие
правила
.
23
1
.
При
сложении
и
вычитании
все
слагаемые
округляют
до
сомни
-
тельной
цифры
,
стоящей
в
самом
высшем
разряде
,
а
затем
выполняют
сложение
.
Например
,
3,14 0,847 0,936 0,0646 0,0483
3,14 0,85 0,94 0,06 0,05 5,04.
x
=
+
+
+
+
»
»
+
+
+
+
=
Если
округления
не
делать
,
то
сумма
будет
равна
5,0359,
где
послед
-
ние
цифры
сомнительны
,
поскольку
в
первом
слагаемом
верных
цифр
две
,
третья
–
сомнительная
,
а
далее
могут
быть
неизвестные
цифры
.
Округле
-
ние
существенно
упростило
получение
результата
без
потери
точности
.
При
вычитании
близких
по
величине
чисел
возможна
потеря
относи
-
тельной
точности
.
Например
,
при
вычислении
разности
5,7275 5,7232 0,0043
x
=
-
=
исходные
данные
имеют
пять
значащих
цифр
,
а
результат
–
две
значащих
цифры
,
причём
только
одну
верную
цифру
.
Увеличение
точности
в
таких
случаях
возможно
только
путём
изменения
метода
измерений
и
,
следова
-
тельно
,
использования
расчётной
формулы
,
не
содержащей
разности
близ
-
ких
величин
.
2.
При
умножении
и
делении
в
полученном
результате
будет
столько
значащих
цифр
,
сколько
их
содержится
в
исходном
данном
с
наименьшим
количеством
значащих
цифр
.
Предварительно
следует
округлить
все
чис
-
ла
,
оставляя
одну
запасную
цифру
.
Например
,
0,035835 62,5 0,058 62,5 2,23.
x
=
×
»
×
»
3.
При
возведении
в
степень
и
извлечении
корня
у
приближённого
числа
следует
оставить
количество
значащих
цифр
,
равное
их
числу
в
ос
-
новании
.
Например
,
3
2,84
22,9.
x
=
»
Число
,
полученное
в
результате
извлечения
корня
любой
степени
,
должно
содержать
столько
же
значащих
цифр
,
сколько
их
содержалось
в
числе
под
корнем
.
Например
,
8,4700 2,9103.
x
=
»
4.
При
логарифмировании
в
мантиссе
приближённого
числа
должно
быть
столько
же
значащих
цифр
,
сколько
их
содержится
в
логарифмируе
-
мом
числе
.
Например
,
ln 25,0 3,22.
»
Результат
измерений
записывается
в
виде
,
определяемом
формулой
(5.3).
Причём
,
сначала
округляется
погрешность
,
а
затем
–
среднее
значение
.
Правило
округления
погрешностей
.
При
числе
измерений
,
равном
10,
погрешность
определения
величины
s
превышает
30 %.
Поэтому
дос
-
таточно
,
чтобы
абсолютная
погрешность
содержала
одну
значащую
цифру
,
если
она
больше
трёх
,
и
две
значащие
цифры
,
если
первая
из
них
меньше
четырёх
.
Например
,
если
Δ
х
=
0,523,
то
погрешность
после
округления
со
-
24
держит
одну
значащую
цифру
:
Δ
х
= 0,5.
Если
Δ
х
= 0,123,
то
в
результате
округления
погрешность
содержит
две
значащие
цифры
:
Δ
х
= 0,12.
Затем
следует
округлить
среднее
значение
измеренной
величины
.
Правило
округления
среднего
значения
:
1)
среднее
значение
и
погрешность
следует
обязательно
выражать
в
одинаковых
единицах
,
2)
последняя
цифра
среднего
значения
должна
принадлежать
к
то
-
му
же
разряду
,
что
и
у
абсолютной
погрешности
.
Например
,
если
x =
4397,63
и
x
D
=
12,7,
то
результат
следует
записать
в
виде
:
x
=
4398
±
13
(
абсолютная
погрешность
содержит
две
значащие
цифры
,
так
как
первая
значащая
цифра
«1» –
меньше
четырёх
).
Десятичный
порядок
среднего
значения
и
абсолютной
погрешности
должен
быть
одинаковым
.
Например
,
запись
х
=
(9,857
∙
10
9
±
7
∙
10
6
)
Па
не
допустима
,
так
как
она
не
позволяет
определить
,
какая
цифра
среднего
значения
является
ненадёжной
.
Правильная
запись
представленного
ре
-
зультата
имеет
следующий
вид
:
х
=
(9,987
±
0,007)
∙
10
9
Па
.
В
качестве
абсолютной
погрешности
табличной
величины
принимают
пять
единиц
разряда
,
следующего
за
разрядом
последней
,
сохраняемой
в
раз
-
ряде
цифры
.
Например
,
если
принять
значение
числа
p
=
3,1425926
…
равным
3,14,
то
относительная
погрешность
определения
числа
p
равна
0,05 %.
Округления
необходимы
,
поскольку
излишне
большое
число
приво
-
димых
десятичных
знаков
создаёт
ложное
представление
о
большой
точ
-
ности
результата
.
9.
Построение
графиков
по
экспериментальным
данным
Результаты
экспериментов
обычно
представляют
как
в
виде
таблиц
,
так
и
в
графической
форме
.
Графики
используют
для
различных
целей
.
Во
-
первых
,
графики
строят
для
определения
некоторых
величин
–
угол
наклона
линейной
зависимости
или
отрезок
,
отсекаемый
на
коорди
-
натной
оси
.
Во
-
вторых
,
графики
используют
для
повышения
наглядности
пред
-
ставления
результатов
.
Графики
позволяют
также
наглядно
сравнивать
экспериментальные
результаты
с
теоретической
кривой
.
В
-
третьих
,
с
помощью
графиков
устанавливают
эмпирическое
соот
-
ношение
между
двумя
величинами
.
При
построении
графиков
в
физике
принято
придерживаться
сле
-
дующих
основных
правил
.
25
1.
Для
построения
графиков
следует
использовать
специальную
бу
-
магу
:
миллиметровую
,
логарифмическую
или
полулогарифмическую
.
2.
По
горизонтальной
оси
откладывают
независимую
переменную
,
то
есть
величину
,
значения
которой
задаёт
сам
экспериментатор
,
а
по
вер
-
тикальной
оси
–
величину
,
которую
определяют
в
ходе
эксперимента
.
Та
-
ким
образом
,
по
горизонтальной
оси
откладывают
причину
,
а
по
верти
-
кальной
оси
–
следствие
.
3.
При
построении
графиков
следует
разумно
выбирать
масштаб
,
чтобы
экспериментальные
точки
располагались
на
всей
площади
листа
.
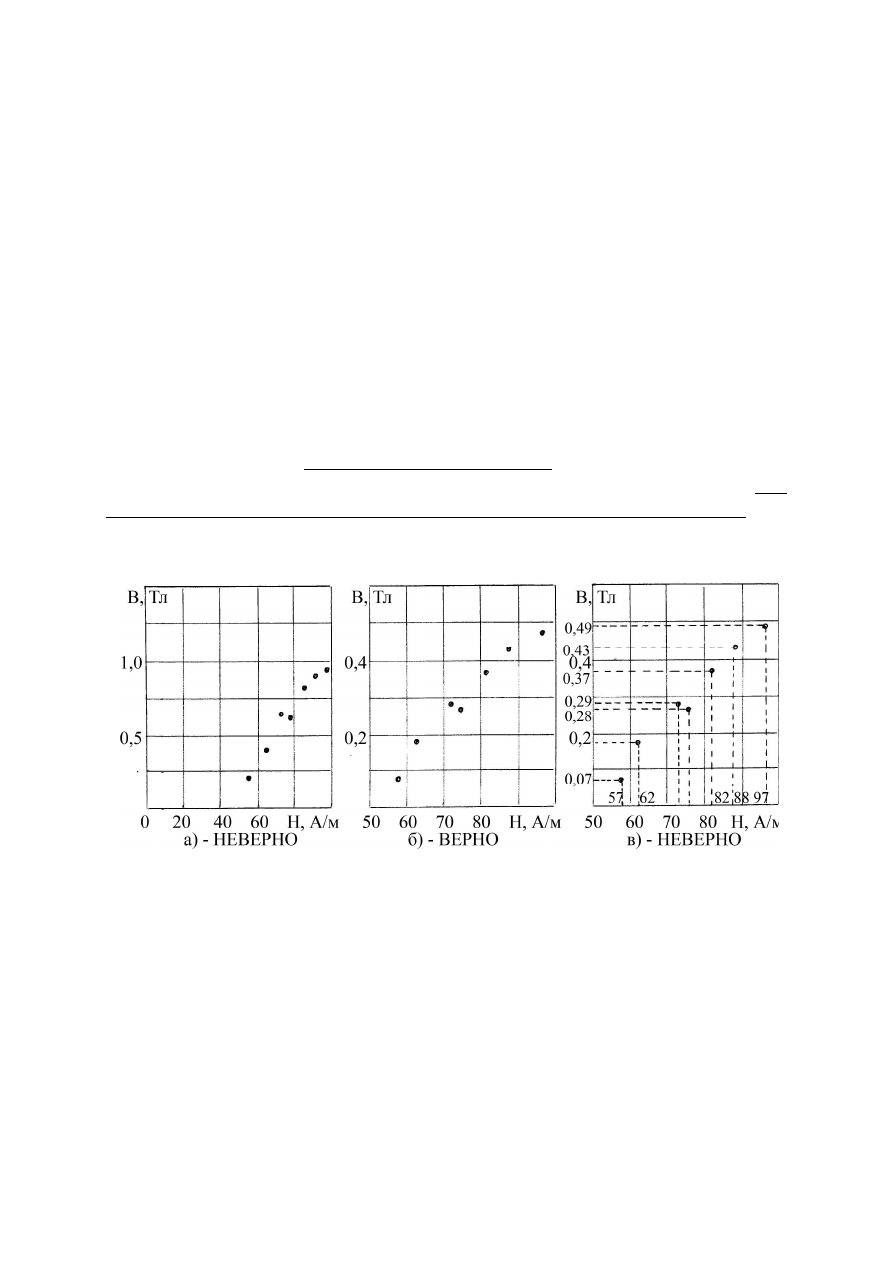
На
рис
. 9.1
на
левом
графике
(
рис
. 9.1
а
)
масштаб
выбран
неверно
,
и
экспериментальные
точ
-
ки
расположились
в
правом
нижнем
углу
рисунка
.
Чтобы
этого
избежать
,
сле
-
дует
выбрать
более
крупный
масштаб
по
оси
ординат
и
сместить
нуль
на
оси
абсцисс
,
как
это
сделано
на
рис
. 9.1
б
.
Масштаб
должен
быть
удобным
.
Кле
-
точка
графика
может
соответствовать
,
например
, 0,1; 0,2; 0,5; 1; 2; 5; 10
едини
-
цам
измеряемой
величины
,
но
не
должна
соответствовать
,
например
, 3; 2,4; 7;
9
единицам
величины
.
Оси
градуируют
равномерно
.
4.
Точки
,
наносимые
на
графики
,
следует
изображать
чётко
и
ясно
.
Ни
-
каких
линий
и
отметок
,
поясняющих
построение
точек
наносить
нельзя
,
по
-
скольку
это
загромождает
рисунок
и
мешает
анализу
результата
.
Недопустимо
наносить
на
оси
значения
координат
точек
,
как
это
показано
на
рис
. 9.1
в
.
Рис
. 9.1
Точки
,
полученные
в
разных
условиях
(
например
,
при
нагревании
и
охла
-
ждении
)
следует
обозначать
разными
символами
.
Это
помогает
обнару
-
жить
новые
явления
.
На
рис
. 9.2
а
показано
неверное
,
а
на
рис
. 9.2
б
–
вер
-
ное
обозначение
точек
,
соответствующих
результатам
,
полученным
в
раз
-
ных
условиях
.
На
левом
графике
виден
только
разброс
точек
,
а
правый
график
показывает
,
что
разброс
точек
невелик
,
но
точки
,
полученные
при
нагревании
и
охлаждении
,
лежат
на
разных
кривых
.