ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.04.2021
Просмотров: 418
Скачиваний: 1
31
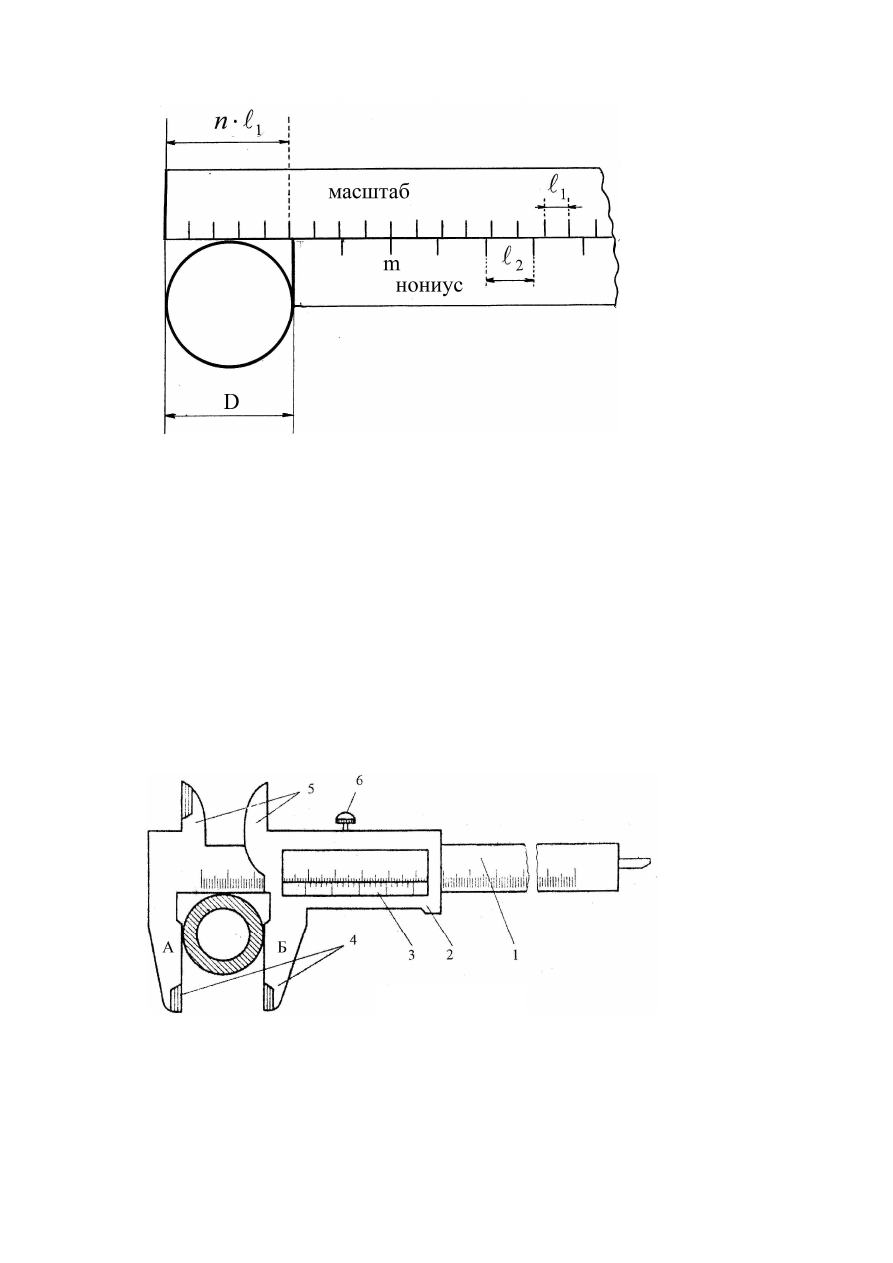
Рис
. 11.2
У
изображённого
на
рис
. 11.2
нониуса
деления
изображены
вдвое
реже
,
чем
на
масштабной
линейке
,
что
не
меняет
правил
отсчёта
.
Как
вид
-
но
и
рис
. 11.2:
1
D n
m
d
= × + ×
l
. (11.3)
Здесь
n
–
целое
число
делений
масштаба
,
m
–
номер
деления
нониуса
,
совпа
-
дающего
с
одним
из
делений
масштаба
(
если
ни
одно
из
делений
нониуса
не
совпадает
в
точности
с
делениями
масштаба
,
в
качестве
m
берут
номер
деле
-
ния
,
которое
ближе
других
подходит
к
одному
из
делений
масштаба
).
Аналогичным
образом
можно
строить
не
только
линейные
,
но
и
угловые
нониусы
.
Нониусами
снабжаются
штангенциркули
,
микрометры
и
многие
другие
измерительные
приборы
.
3.
Штангенциркуль
(
рис
. 11.3)
представляет
собой
линейку
с
делениями
,
снабжённую
двумя
выступами
4.
Выступ
А
неподвижен
,
выступ
Б
соединён
с
нониусом
3,
свободно
скользящим
вдоль
линейки
1.
Когда
выступы
А
и
Б
плот
-
но
сдвинуты
,
нуль
нониуса
находится
против
нуля
линейки
.
Когда
выступ
Б
Рис
. 11.3
32
отодвинут
от
выступа
А
,
то
расстояние
между
ними
равно
длине
,
на
которую
нуль
нониуса
передвинулся
вдоль
линейки
от
её
нуля
.
При
этом
по
основной
шкале
линейки
отсчитывается
n
делений
,
по
шкале
нониуса
–
доли
деления
,
для
чего
определяется
деление
m
нониуса
3
,
совпадающее
с
каким
-
либо
делением
основной
шкалы
.
Линейный
размер
тела
находят
по
формуле
:
m
L
n
N
æ
ö
=
+
×
ç
÷
è
ø
l
,
где
N
–
число
делений
нониуса
,
равное
N
– 1
делению
основной
шкалы
,
l
–
цена
деления
основной
шкалы
.
Стопорный
винт
6
предназначен
для
стабилизации
положения
под
-
вижной
шкалы
в
процессе
измерений
.
Выступы
5
предназначены
для
из
-
мерения
внутренних
размеров
тел
.
4.
Для
более
точных
измерений
используют
микрометр
(
рис
. 11.4).
Он
состоит
из
двух
частей
:
скобы
1
и
микрометрического
винта
,
связанно
-
го
с
барабаном
7,
на
остром
срезе
которого
имеется
круговая
шкала
6.
Рис
. 11.4
При
работе
с
микрометром
следует
иметь
в
виду
,
что
винт
с
малым
шагом
превращает
незначительные
усилия
руки
,
поворачивающей
барабан
микрометра
,
в
большие
силы
,
действующие
на
измеряемый
объект
и
на
сам
микрометр
.
Это
может
привести
как
к
деформации
предмета
,
так
и
к
повреждению
микрометра
.
Для
уменьшения
ошибки
,
связанной
с
сильным
и
неодинаковым
сжатием
измеряемых
предметов
,
рукоятка
микрометра
снабжена
специальной
головкой
9 –
трещоткой
,
позволяющей
создавать
небольшое
,
соответствующее
стандартам
,
давление
на
измеряемый
объект
.
Шкала
6
барабана
7
имеет
n
=
50
делений
.
Если
шаг
винта
равен
h
мм
,
то
при
повороте
барабана
на
одно
деление
винт
переместится
на
h
n
=
0,01
мм
.
Величина
h
n
называется
точностью
микрометрического
винта
.
Следовательно
,
при
одном
повороте
барабана
подвижная
часть
3
переместится
на
0,5
мм
,
что
соответствует
появлению
риски
на
верхней
части
шкалы
5.
Для
перемещения
подвижной
части
3
на
1
мм
необходимо
повернуть
барабан
7
два
раза
.
33
Перед
измерением
следует
тщательно
протереть
измерительные
по
-
верхности
и
проверить
установку
нуля
.
Измеряемое
тело
зажимается
между
неподвижным
торцом
2
и
подвижным
стержнем
3
микрометрического
винта
.
Вращение
винта
следует
производить
только
при
помощи
трещотки
9.
Затем
следует
зафиксировать
микрометр
с
помощью
винта
4,
вынуть
измеряемое
те
-
ло
и
записать
показание
микрометра
L
с
помощью
следующей
формулы
:
Ш
Н
L
d
=
+ +
l
l
,
где
Ш
l
–
число
целых
миллиметров
,
отсчитанное
по
шкале
5
(
на
рис
. 11.4
Ш
l
=
1
мм
);
d
принимает
значения
:
ноль
,
если
барабан
переместился
на
расстояние
,
меньшее
0,5
мм
и
0,5
мм
,
если
барабан
переместился
на
рас
-
стояние
,
большее
0,5
мм
(
на
рис
. 11.4
d
=
0,5
мм
);
Н
l
–
число
делений
,
от
-
считанное
по
шкале
6
нониуса
(
на
рис
. 11.4
Н
l
=
0,17
мм
).
Таким
образом
,
результат
измерения
,
соответствующий
рис
. 11.4,
равен
:
L
=
1,67
мм
.
Иногда
шкала
микрометра
бывает
сбита
:
при
соприкосновении
стержней
2
и
3
показание
микрометра
отличается
от
нуля
.
В
этом
случае
микрометр
нуждается
в
регулировке
.
Регулировку
микрометра
студентам
выполнять
не
разрешается
.
Следует
обратиться
к
преподавателю
.
Порядок
выполнения
работы
1.
Изучить
принципы
измерения
линейных
размеров
тел
с
помощью
штангенциркуля
и
микрометра
.
2.
Штангенциркулем
измерить
5
раз
толщину
h
пластинки
или
диа
-
метр
цилиндра
(
по
указанию
преподавателя
).
Результаты
измерений
запи
-
сать
в
столбик
2
таблицы
11.1.
3.
Микрометром
измерить
5
раз
диаметр
d
проволоки
или
толщину
пластинки
(
по
указанию
преподавателя
).
Результаты
измерений
записать
в
столбик
5
таблицы
11.1.
Таблица
11.1
Результаты
измерений
штангенциркулем
Результаты
измерений
микрометром
№
i
h
[
мм
]
i
h
h
-
[
мм
]
(
)
2
i
h
h
-
[
мм
2
]
i
d
[
мм
]
i
d
d
-
[
мм
]
(
)
2
i
d
d
-
[
мм
2
]
1
2
3
4
5
6
7
1
2
3
4
5
Среднее
значение
-
-
4.
Рассчитать
средние
значения
измеряемых
величин
(
нижняя
строка
таблицы
),
а
также
случайные
отклонения
(
столбики
3
и
6
таблицы
)
и
квад
-
34
раты
отклонений
(
столбики
4
и
8
таблицы
).
Просуммировать
результаты
вычислений
в
столбиках
4
и
8
таблицы
.
5.
Для
доверительной
вероятности
a
=
0,90
рассчитать
случайную
погрешность
СЛ
h
D
и
СЛ
d
D
,
используя
формулу
(3.16).
Коэффициент
Стью
-
дента
для
данного
значения
доверительной
вероятности
и
числа
измерений
n
= 5
с
помощью
табл
. 1
приложения
.
6.
Оценить
инструментальную
погрешность
(
ПР
h
D
и
ПР
d
D
)
и
рассчи
-
тать
суммарную
погрешность
с
помощью
формулы
(5.2).
7.
Записать
результат
в
соответствии
с
формулами
(5.3)
и
(5.4),
ука
-
зав
доверительную
вероятность
.
8.
Сделать
выводы
.
Контрольные
вопросы
1.
Что
называется
измерением
?
Какие
виды
измерений
Вам
известны
?
2.
Перечислите
основные
характеристики
измерений
.
3.
Что
называется
систематической
погрешностью
,
и
чем
она
обусловлена
?
4.
Что
называется
гистограммой
?
От
чего
зависит
ширина
гистограммы
:
от
точности
измерительного
прибора
или
от
совершенства
метода
?
Ответ
обосновать
.
5.
Как
влияет
точность
измерительного
прибора
на
форму
гистограммы
?
Что
называется
вероятностью
и
плотностью
вероятности
?
Как
точность
метода
влияет
на
ширину
доверительно
интервала
?
6.
Изложить
методику
оценки
случайной
погрешности
при
прямых
равно
-
точных
измерениях
.
7.
Как
оценить
и
учесть
инструментальную
погрешность
?
8.
Изложить
методику
оценки
случайной
погрешности
косвенных
измере
-
ний
.
Привести
примеры
.
Вывести
формулу
для
расчёта
случайной
погреш
-
ности
(
для
указанной
преподавателем
формулы
).
9.
Что
называется
промахом
?
Как
выявляют
промахи
?
10.
Как
устроен
нониус
?
Изложить
методику
его
расчёта
.
11.
Как
устроен
штангенциркуль
?
Изложить
методику
измерений
с
помо
-
щью
штангенциркуля
.
12.
Как
устроен
микрометр
?
Изложить
методику
измерений
с
помощью
микрометра
.
35
12.
РАБОТА
№
1-
б
.
ОПРЕДЕЛЕНИЕ
ПЛОТНОСТИ
ТВЁРДОГО
ТЕЛА
,
ИМЕЮЩЕГО
ПРАВИЛЬНУЮ
ГЕОМЕТРИЧЕСКУЮ
ФОРМУ
Цель
работы
:
определение
плотности
твёрдого
тела
правильной
гео
-
метрической
формы
,
изучение
методов
обработки
результатов
изме
-
рений
.
Приборы
и
принадлежности
:
рычажные
весы
,
разновесы
,
штанген
-
циркуль
,
микрометр
,
исследуемые
тела
.
Краткая
теория
Плотностью
однородного
вещества
называется
величина
( )
r
,
рав
-
ная
его
массе
( )
m
,
содержащейся
в
единице
объёма
( )
V
:
3
[
кг
/
м
]
m V
r
=
. (12.1)
Плотность
неоднородного
вещества
в
определённой
точке
–
предел
отношения
массы
тела
( )
m
к
его
объёму
( )
V
,
если
объём
стягивается
в
этой
точке
.
Средняя
плотность
неоднородного
тела
также
определяется
формулой
(12.1).
Иногда
применяется
понятие
относительной
плотности
.
Например
,
плотность
вещества
,
определяемая
отношением
к
плотности
воды
при
температуре
+4
˚С
.
Плотность
и
удельный
вес
(
,
P V P
g
=
–
вес
вещества
,
объём
которого
равен
V
)
связаны
соотношением
g
g r
= ×
.
Методы
измерения
плотности
веществ
весьма
разнообразны
.
Плот
-
ность
твёрдых
тел
находят
,
например
,
путём
точного
измерения
массы
те
-
ла
и
его
объёма
с
последующим
использованием
формулы
(12.1).
Порядок
выполнения
работы
Задание
1.
Измерение
линейных
размеров
тел
.
1.
Измерить
штангенциркулем
или
микрометром
пять
раз
линейные
размеры
тела
.
Вычислить
средние
значения
.
Результаты
измерений
занести
в
табл
. 12.1
и
12.2.
2.
Рассчитать
погрешности
прямых
измерений
.
Определить
среднее
значение
и
оценить
погрешность
.
Задание
2.
Измерение
массы
тел
.
Инструментальная
погрешность
измерения
массы
тела
с
помощью
рычажных
технических
весов
равна
±
0,02
г
.
Случайной
погрешностью
измерений
при
таком
значении
инструментальной
погрешности
можно
пренебречь
.