ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.04.2021
Просмотров: 1355
Скачиваний: 16
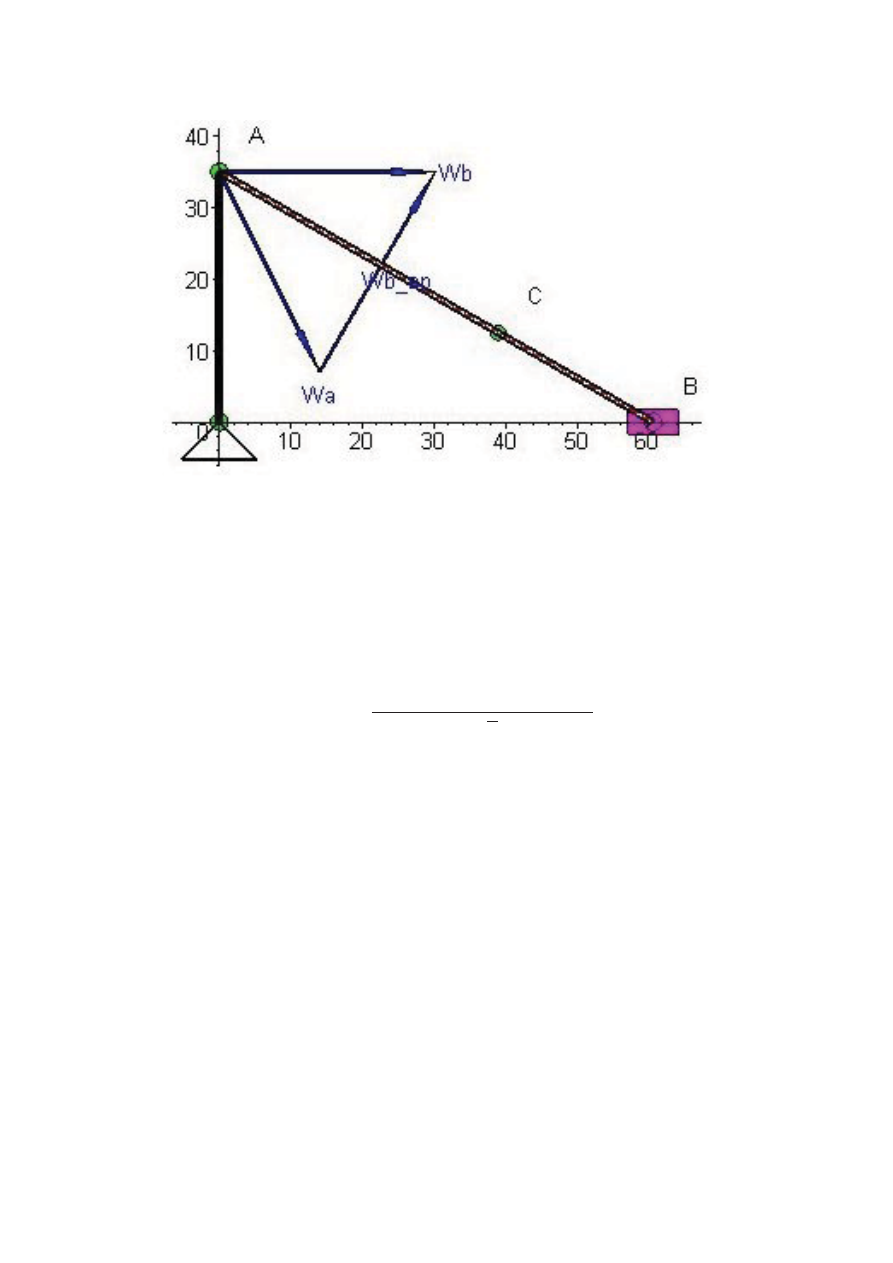
Найдем ускорение точки
C
. Воспользуемся формулой
¯
w
C
= ¯
w
A
+ ¯
w
вр
C
(
A
)
+ ¯
w
ц
C
(
A
)
и запишем ее в проекциях на координатные оси.
> W[’C_x’] := W[‘A_вр‘]+epsilon[’AB’]*AC*sin(psi):
W[’C_y’] := -W[‘A_ц‘]+epsilon[’AB’]*AC*cos(psi):
W[’C’] := sqrt(W[’C_x’]^2 + W[’C_y’]^2);
W
C
:=
(280 + 120
√
3)
3
+ 40000
> w4 := vector([W[’C_x’]/W_размер, W[’C_y’]/W_размер]):
Wc := arrow(pointC, w4, .35, 1, .20, color=blue):
display(draw(Pi/2),
Wa, Wb, Wc,
textplot([w1[’x’]+dxy, 35+w1[’y’]+dxy, ’Wa’],
color=blue),
textplot([pointB[1]+w2[1]+dxy, dxy, ’Wb’],
color=blue),
textplot([pointC[1]+w4[1]-dxy,
pointC[2]+w4[2]+dxy, ’Wc’],
color=blue),
scaling=CONSTRAINED);
96
Ответ
> ‘Скорости точек:‘;
V[‘В‘]=V[’A’].‘см/с‘, V[‘С‘]=V[’C’].‘см/с‘;
‘Угловая скорость звена АВ:‘;
’omega[‘AB‘]’=omega[’AB’];
‘Ускорения точек:‘;
’W[‘B‘]’=evalf(W[B]), ’W[‘C‘]’=evalf(W[C]);
‘Угловое ускорение звена АВ:‘;
’epsilon[AB]’=evalf(epsilon[’AB’]);
Скорости точек:
V
B
= 140
см/с,
V
C
= 140
см/с
Угловая скорость звена
AB
:
ω
AB
= 0
Ускорения точек:
W
B
= 603
.
3161509
,
W
C
= 527
.
2511872
Угловое ускорение звена
AB
:
ε
= 9
.
237604309
6.2
Сложное движение точки
Точка
M
движется относительно тела
D
. Позаданным уравнени-
ям относительного движения точки
M OM
=
S
(
t
) = 10(1 + sin 2
πt
)
и
движения тела
ϕ
=
ϕ
(
t
) = 4
t
+ 1
.
6
t
2
определить для заданного момента
времени
t
=
1
8
абсолютную скорость и абсолютное ускорение точки
M
.
Схема механизма показана на рисунке.
97
Решение
> restart:
> S := t -> 10*(1+sin(2*Pi*t)):
phi := t -> 4*t+1.6*t^2:
> with(plots):
with(plottools):
> pos := proc(psi, s, t1)
local
point_x, point_y;
point_x := s*cos(psi);
point_y := s*sin(psi);
PLOT(plottools[point]([point_x, point_y],
symbol=circle,
color=red, symbolsize=15),
op(plot([S(t), phi(t), t=0 .. t1],
coords=polar, color=green)),
line([0, 0], [25*cos(psi), 25*sin(psi)],
color=red, linestyle=4));
end proc:
> pos2 := proc(psi, s, t1)
local
телоD, телоB,
pointB, point1, point2, point3, point4,
h, OA;
OA := 30;
h := 0.25;
point1 := [h*cos(psi+Pi/2),h*sin(psi+Pi/2)];
point2 := [h*cos(psi+Pi/2) + OA*cos(psi),
h*sin(psi+Pi/2) + OA*sin(psi)];
point3 := [point2[1] + 2*h*cos(psi+3*Pi/2),
point2[2] + 2*h*sin(psi+3*Pi/2)];
point4 := [h*cos(psi+3*Pi/2), h*sin(psi+3*Pi/2)];
98
телоD := polygon([point1, point2, point3, point4],
linestyle=1, thickness=1,
color=gray);
pointB := [s*cos(psi), s*sin(psi)];
h := 1.5;
point1 := [pointB[1] + h*cos(psi+5*Pi/6),
pointB[2] + h*sin(psi+5*Pi/6)];
point2 := [pointB[1] + h*cos(psi+Pi/6),
pointB[2] + h*sin(psi+Pi/6)];
point3 := [pointB[1] + h*cos(psi-Pi/6),
pointB[2] + h*sin(psi-Pi/6)];
point4 := [pointB[1] + h*cos(psi-5*Pi/6),
pointB[2] + h*sin(psi-5*Pi/6)];
телоB := polygon([point1, point2, point3, point4],
linestyle=1, thickness=1);
display(pos(psi, s, t1),
телоD, телоB,
disk(pointB, h/3, color=red));
end proc:
> N_frames := 200:
for i from 0 to N_frames do
tau := Pi/N_frames*i;
p[i] := pos2(phi(tau), S(tau), Pi);
end do:
> plots[display](seq(p[i], I = 0 .. 200),
insequence=true,
scaling=constrained);
На рисунке изображена траектория точки в неподвижных коорди-
натах при
t
о т 0 до
π
.
99
> pos(phi(1/8), S(1/8), 3/16);
’phi’=evalf(convert(phi(1/8), degrees));
’S’=S(1/8);
Положение точки
M
относительно тела
D
в момент времени
1
8
определяется расстоянием
S
1
8
= 10 + 5
√
2
, а положение тела
D
—
углом
ϕ
1
8
, равным
30
◦
градусов (см. рисунок).
Абсолютная скорость точки будет равна векторной сумме двух ско-
ростей — относительной и переносной:
¯
V
абс
= ¯
V
от
+ ¯
V
пер
.
При этом, чтобы найти относительную скорость, надо мысленно
«заморозить» переносное движение (т.е. вращение). Тогда:
¯
V
от
=
d
dt
S
(
t
)
,
а направлена эта скорость будет вдоль тела
D
.
> V := unapply(diff(S(t), t), t);
V
:=
t
−→
20 cos 2
πt
·
π
> V_размер := 6:
V_отн := V(1/8)/V_размер:
dxy := 0.25:
> x := S(1/8)*cos(phi(1/8)):
y := S(1/8)*sin(phi(1/8)):
100