ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 1739
Скачиваний: 2
Р
АЗДЕЛ
3
50
где
а
, b, c
−
некоторые
параметры
,
определяемые
из
испытаний
при
простей
-
ших
напряженных
состояниях
,
(
) (
) (
)
2
1
3
2
3
2
2
2
1
2
2
σ
σ
σ
σ
σ
σ
σ
−
+
−
+
−
=
i
,
(3.2)
.
3
2
1
σ
σ
σ
+
+
=
I
(3.3)
Здесь
:
3
2
1
,
,
σ
σ
σ
–
главные
напряжения
.
Следуя
гипотезе
Мора
,
предположим
,
что
прочность
материала
практиче
-
ски
зависит
только
от
тех
членов
выражений
(3.2)
и
(3.3),
которые
определяют
разность
и
сумму
наибольшего
и
наименьшего
компонентов
напряжений
.
То
-
гда
,
из
(3.1)
при
а
= 0
получим
следующее
выражение
:
(
)
(
)
c
b
=
+
+
−
3
1
2
3
1
2
1
σ
σ
σ
σ
.
(3.4)
Параметры
b
и
с
определим
из
(3.4)
в
результате
испытаний
горных
пород
при
простейших
напряженных
состояниях
.
Получим
:
–
при
одноосном
сжатии
в
предельном
состоянии
c
bR
R
c
c
=
+
2
2
1
;
(3.5)
–
при
одноосном
растяжении
c
bR
R
p
p
=
−
2
2
1
.
(3.6)
Решая
совместно
уравнения
(3.5)
и
(3.6),
находим
,
что
)
1
(
2
1
−
=
ψ
c
R
b
;
ψ
⋅
=
2
2
1
c
R
c
,
(3.7)
где
c
p
R
R
=
ψ
.
Подставив
значения
параметров
(3.7)
в
соотношение
(3.4),
получим
сле
-
дующее
условие
прочности
2
:
2
Условие
прочности
(3.8)
было
получено
Л
.
Я
.
Парчевским
и
А
.
Н
.
Шашенко
в
статье
: «
О
размерах
области
пла
-
стических
деформаций
вокруг
выработок
//
Изв
.
ВУЗов
.
Горный
журнал
.– 1998.–
№
3.–
С
. 39-42».
К
РИТЕРИИ
ПРОЧНОСТИ
В
ГЕОМЕХАНИКЕ
51
(
)
(
) (
)
0
1
3
1
2
2
3
1
=
+
−
−
−
−
σ
σ
ψ
ψ
σ
σ
c
c
R
R
,
(3.8)
или
в
общем
случае
напряженного
состояния
(
)
(
)
(
)
0
1
4
2
2
2
=
+
−
−
−
+
−
y
x
c
c
xy
y
x
R
R
σ
σ
ψ
ψ
τ
σ
σ
.
(3.9)
Из
выражения
(3.8)
получим
k
2
3
1
=
−
σ
σ
,
(3.10)
где
(
) (
)
3
1
2
1
5
,
0
σ
σ
ψ
ψ
+
−
+
=
c
c
R
R
k
.
(3.11)
Заметим
,
что
при
осесимметричном
распределении
напряжений
σ
1
+
σ
3
=
σ
r
+
σ
θ
=const
.
Из
этого
следует
,
что
выражение
(3.10)
является
по
своей
сути
условием
прочности
Треска
-
Сен
-
Венана
.
В
общем
же
случае
напряженного
состояния
пра
-
вая
часть
условия
(3.10)
зависит
от
значений
компонентов
напряжения
.
Для
материалов
,
одинаково
сопротивляющихся
сжатию
и
растяжению
,
ψ
=1
.
В
этом
случае
из
выражения
(3.8)
получим
теорию
прочности
Кулона
.
Обозначим
соответственно
максимальное
касательное
напряжение
и
величину
,
характеризующую
вид
напряженного
состояния
,
как
2
3
1
σ
σ
τ
−
=
и
2
3
1
σ
σ
σ
+
=
.
То
-
гда
выражение
(3.8)
с
учетом
принятых
обозначений
примет
вид
(
)
0
1
2
4
2
2
=
−
−
−
ψ
ψ
σ
τ
c
c
R
R
.
(3.12)
Зависимость
(3.12)
в
системе
координат
«
σ
τ
−
»
представляет
уравнение
параболы
,
которая
является
выпуклой
и
непрерывной
кривой
.
В
системе
же
координат
«
3
1
σ
σ
−
»
уравнение
(3.8)
имеет
вид
параболы
,
равнонаклоненной
к
осям
и
открытой
со
стороны
сжимающих
напряжений
,
что
соответствует
требованию
симметричности
условия
возникновения
предельно
-
го
напряженного
состояния
(
рис
. 3.1).
Р
АЗДЕЛ
3
52
С
увеличением
ве
-
личины
ψ
от
0
до
1
па
-
рабола
вытягивается
в
сторону
всестороннего
растяжения
,
что
под
-
тверждается
опытами
Г
.
В
.
Ужика
[40].
И
,
на
-
конец
,
при
ψ
= 1
парабо
-
ла
вырождается
в
две
параллельные
прямые
,
соответствующие
теории
«
энергии
формоизменения
».
Таким
образом
,
полученное
условие
прочности
отвечает
требованиям
постулата
Друккера
[74]
и
соответствует
современным
представлениям
о
природе
разрушения
твердых
тел
[73, 65].
Если
в
изложенных
выше
рассуждениях
не
прибегать
к
гипотезе
Мора
о
независимости
прочности
материала
от
среднего
по
величине
касательного
на
-
пряжения
2
σ
,
то
на
основе
зависимости
(3.1)
при
а
= 0
может
быть
получена
теория
прочности
П
.
П
.
Баландина
[74],
аналитический
критерий
которой
для
предельного
состояния
имеет
вид
:
[
]
.
2
)
(
)
(
)
(
4
)
(
)
1
(
2
)
)(
1
(
2
1
3
2
3
2
2
2
1
2
3
2
1
2
3
2
1
ψ
σ
σ
σ
σ
σ
σ
ψ
σ
σ
σ
ψ
ψ
σ
σ
σ
ψ
−
+
−
+
−
+
+
+
−
+
+
+
+
−
=
c
R
(3.13)
Выражение
(3.8)
можно
привести
к
такому
же
виду
ψ
σ
σ
ψ
σ
σ
ψ
σ
σ
ψ
2
)
(
4
)
(
)
1
(
)
)(
1
(
2
3
1
2
3
1
2
3
1
−
+
+
−
+
+
−
=
c
R
.
(3.14)
Из
(3.13)
при
0
2
=
σ
получим
критерий
прочности
для
плоского
напряжен
-
ного
состояния
Рис
. 3.1.
Поверхность
предельных
состояний
К
РИТЕРИИ
ПРОЧНОСТИ
В
ГЕОМЕХАНИКЕ
53
(
)
(
) (
)
(
)
[
]
2
1
3
2
3
2
1
2
3
1
2
3
1
4
1
2
1
2
1
σ
σ
σ
σ
ψ
σ
σ
ψ
ψ
σ
σ
ψ
ψ
−
+
+
+
+
−
+
+
−
=
c
R
. (3.15)
Сравнение
выражений
(3.14)
и
(3.15)
показывает
,
что
это
разные
критерии
,
различие
между
которыми
увеличивается
по
мере
роста
пластических
свойств
материала
(
1
→
ψ
).
Поведение
же
хрупких
материалов
(
0
→
ψ
)
оба
критерия
описываются
примерно
одинаково
и
достаточно
хорошо
[73].
В
аналитических
же
исследованиях
упругопластического
состояния
более
удобным
является
вы
-
ражение
(3.8),
которое
симметрично
относительно
входящих
в
него
компонен
-
тов
напряжений
1
σ
и
3
σ
.
Величина
ψ
для
большинства
горных
пород
редко
превышает
0,1-0,2.
Как
показывает
анализ
зависимости
(3.8),
даже
при
столь
высоком
значении
ψ
ее
можно
принять
равной
нулю
,
обеспечивая
при
этом
в
области
сжимающих
на
-
пряжений
достаточную
точность
.
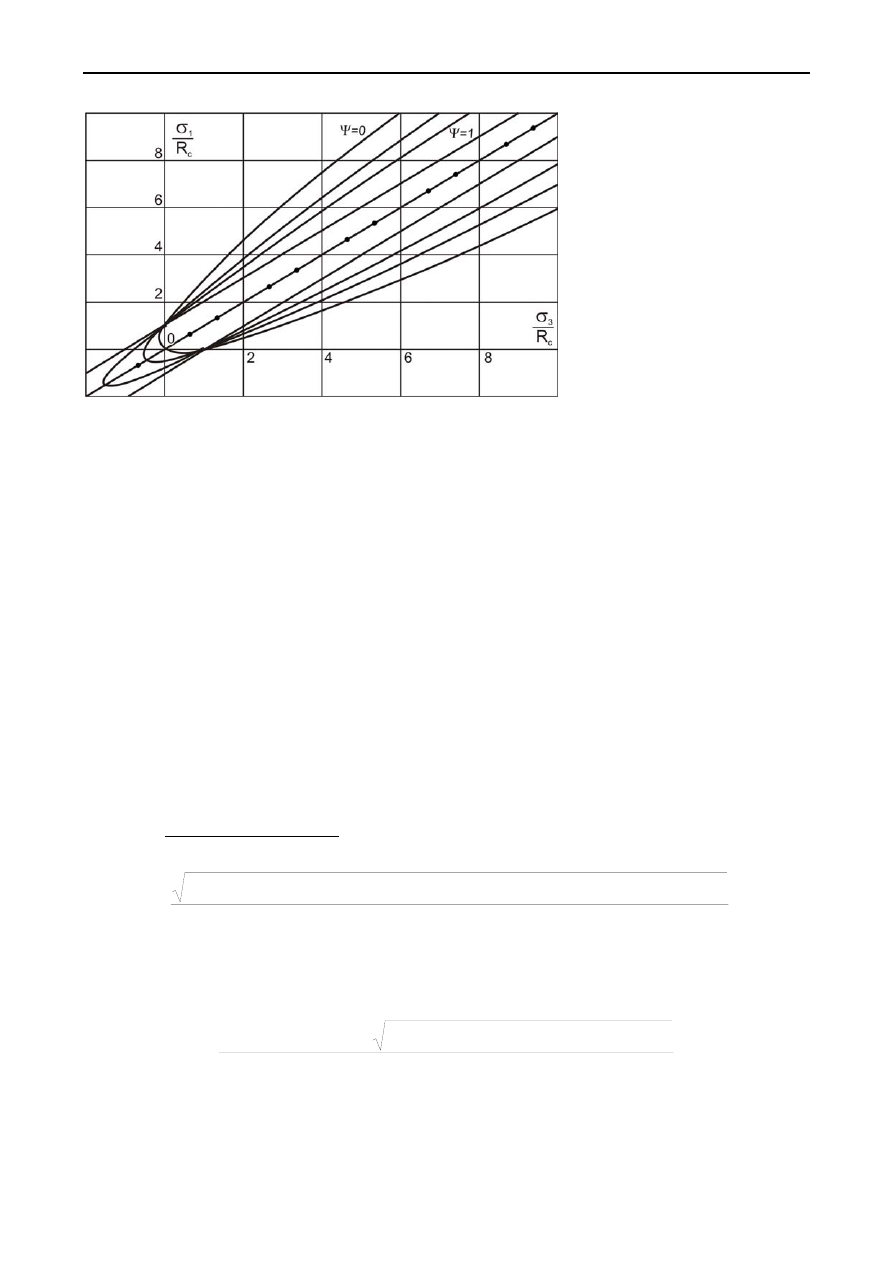
Это
обстоятельство
отражено
на
рис
. 3.2,
где
в
системе
безразмерных
координат
показаны
предельные
кривые
для
различ
-
ных
значений
ψ
.
Уравнение
предельных
огибающих
получено
из
(3.12)
путем
деления
всех
его
членов
на
c
R
.
При
0
=
ψ
из
(3.9)
получим
следующее
частное
выражение
прочности
(
)
3
1
3
1
σ
σ
σ
σ
+
=
−
c
R
.
(3.16)
Рассмотрим
поведение
кривых
в
области
растяжения
(
см
.
рис
. 3.2).
При
значении
5
,
0
p
ψ
графики
пересекают
ось
абсцисс
в
точке
,
находящейся
от
на
-
чала
координат
на
расстоянии
,
меньшем
p
R
.
Точка
пересечения
соответствует
двухосному
равнокомпонентному
растяжению
(
3
1
σ
σ
=
).
Следовательно
,
проч
-
ность
горных
пород
,
которые
по
структурным
особенностям
приближаются
к
хрупким
,
при
двухосном
равнокомпонентном
растяжении
определяется
значе
-
нием
одного
из
компонентов
напряжения
,
меньшим
величины
прочности
на
одноосное
растяжение
.
Таким
образом
,
двухосному
чистому
растяжению
такие
материалы
сопротивляются
хуже
,
чем
одноосному
растяжению
.
Эта
особен
-
ность
для
хрупких
горных
пород
нашла
отражение
в
работе
[125].
Р
АЗДЕЛ
3
54
При
значении
5
,
0
f
ψ
предельные
кривые
пересе
-
кают
ось
абсцисс
в
точке
,
на
-
ходящейся
на
расстоянии
от
начала
координат
,
большем
величины
p
R
,
т
.
о
.,
с
увеличе
-
нием
пластических
свойств
сопротивление
материала
двухосному
чистому
растя
-
жению
становится
больше
сопротивления
одноосному
растяжению
.
Это
обстоятельство
было
подтверждено
известными
опытами
Г
.
В
.
Ужика
с
пластичными
металлами
[40].
Подобное
же
поведение
кривых
в
области
растягивающих
усилий
применительно
к
горным
породам
предполо
-
жил
и
обосновал
М
.
М
.
Протодьяконов
[126].
В
частности
,
с
точки
зрения
со
-
противляемости
внешним
усилиям
влажные
глины
ведут
себя
как
пластичные
металлы
:
на
диаграмме
деформирования
выражена
площадка
текучести
,
при
небольшом
значении
предела
прочности
на
одноосное
сжатие
глины
имеют
практически
линейную
зависимость
«
ε
σ
−
» (
см
.
рис
. 2.6).
Анализ
выражения
(3.12)
показывает
,
что
при
0
=
σ
из
него
вытекает
про
-
стое
состояние
,
связывающее
основные
прочностные
характеристики
:
пределы
прочности
на
одноосное
сжатие
c
R
,
растяжение
p
R
и
сдвиг
τ
R
:
p
c
R
R
R
5
,
0
=
τ
.
(3.17)
Таким
образом
,
по
двум
известным
предельным
характеристикам
всегда
можно
определить
третью
.
Это
обстоятельство
может
быть
полезным
при
установле
-
нии
величины
p
R
,
определение
которой
в
экспериментальных
условиях
сопря
-
жено
со
значительными
трудностями
.
Рис
. 3.2.
Огибающие
предельных
напряжен
-
ных
состояний
для
горных
пород
разной
сте
-
пени
хрупкости