ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 1737
Скачиваний: 2
Р
АЗДЕЛ
2
40
Модель
представляет
собой
стержневую
статически
неопределимую
сис
-
тему
,
нагружаемую
в
режиме
заданных
деформаций
.
Прочность
стержней
и
угол
их
наклона
являются
величинами
случайными
.
Прочность
всей
системы
определяется
суммарной
прочностью
стержней
.
По
мере
их
разрушения
проч
-
ность
механической
системы
снижается
,
однако
на
любом
уровне
нагружения
ее
упругие
свойства
сохраняются
.
Подбирая
соответствующим
образом
стерж
-
ни
с
заданными
деформационными
и
прочностными
характеристиками
,
можно
получить
модель
практически
любого
твердого
тела
.
График
деформирования
такой
модели
показан
на
рис
. 2.10,
б
.
2.2.
Связь
между
напряжениями
и
деформациями
за
пределом
прочно
-
сти
В
упругой
области
напряжения
и
деформации
связаны
известными
соот
-
ношениями
Гука
.
В
области
же
запредельного
деформирования
эти
соотноше
-
ния
нарушаются
.
В
известной
мере
можно
говорить
о
пропорциональности
ме
-
жду
приращениями
напряжений
и
деформаций
[4].
Однако
решение
задач
гео
-
механики
в
перемещениях
с
использованием
таких
зависимостей
сталкивается
со
значительными
математическими
трудностями
.
Гораздо
проще
ввести
в
рассмотрение
некоторую
эмпирическую
зависи
-
мость
между
напряжениями
и
деформациями
,
которая
обеспечивала
бы
доста
-
точную
точность
решения
.
Такая
зависимость
может
быть
получена
,
если
вос
-
пользоваться
предположением
о
подобии
механических
явлений
,
происходя
-
щих
при
«
жестком
»
разрушении
породного
образца
и
произвольной
локальной
точки
массива
в
окрестности
горной
выработки
.
Роль
«
жесткого
»
нагружающе
-
го
устройства
при
этом
играет
упруго
деформирующаяся
область
породной
среды
,
расположенная
за
областью
неупругих
деформаций
.
Нагружение
каждой
локальной
точки
массива
происходит
медленно
,
примерно
со
скоростью
,
про
-
порциональной
скорости
проведения
выработки
.
Напряженное
состояние
в
пределах
выделенной
элементарной
области
яв
-
ляется
сложным
,
трехкомпонентным
.
Прямой
анализ
его
затруднителен
.
Здесь
З
АКОНОМЕРНОСТИ
РАЗРУШЕНИЯ
ГОРНЫХ
ПОРОД
ЗА
ПРЕДЕЛОМ
ПРОЧНОСТИ
41
уместно
воспользоваться
понятием
об
эквивалентном
напряженном
состоянии
,
которое
применяется
при
разработке
аналитических
теорий
прочности
[73].
Введение
этого
понятия
позволяет
от
оценки
сложного
напряженного
состоя
-
ния
перейти
к
оценке
простого
одноосного
сжатия
либо
растяжения
.
Суть
тако
-
го
перехода
сводится
к
следующему
.
Пусть
образец
нагружается
объемно
и
компоненты
нагрузок
возрастают
от
нуля
до
каких
-
то
критических
значений
.
Параллельно
станем
нагружать
такой
же
образец
в
условиях
одноосного
сжатия
(
растяжения
),
увеличивая
нагрузку
от
нуля
до
предела
.
Если
оба
образца
поте
-
ряют
прочность
одновременно
,
то
одноосное
напряженное
состояние
считается
с
точки
зрения
разрушения
эквивалентным
трехосному
.
Тогда
законы
разруше
-
ния
породной
среды
,
находящейся
в
окрестности
выработки
в
условиях
объем
-
ного
сжатия
(
растяжения
),
можно
исследовать
,
изучая
закономерности
дефор
-
мирования
породного
образца
в
условиях
одноосного
напряженного
состояния
.
Для
одиночных
горных
выработок
,
пройденных
в
осадочных
углевмещающих
породах
,
удобным
напряженным
состоянием
является
,
как
правило
,
одноосное
сжатие
.
При
изучении
графиков
де
-
формирования
горных
пород
в
ус
-
ловиях
«
жесткого
»
нагружения
отмечалось
,
что
на
любой
стадии
разрушения
структурных
связей
(
ниспадающая
ветвь
)
образец
со
-
храняет
упругие
свойства
и
неко
-
торую
прочность
,
которая
всегда
ниже
начальной
.
При
этом
образец
благодаря
пластическим
деформа
-
циям
увеличивается
в
объеме
.
Объемная
деформация
v
ε
равна
сумме
радиальной
r
ε
и
осевой
θ
ε
Рис
. 2.11.
Зависимость
относительной
прочности
от
величины
относительного
объемного
разрыхления
Р
АЗДЕЛ
2
42
деформаций
(
v
r
ε
ε
ε
θ
=
+
).
На
рис
. 2.11
показана
зависимость
между
относи
-
тельным
снижением
прочности
на
одноосное
сжатие
c
R
σ
и
соответствующим
относительным
увеличением
объемного
разрыхления
*
v
v
ε
ε
для
исследуемых
литологических
разностей
.
Здесь
∗
v
ε
–
максимальное
относительное
увеличение
объема
в
условиях
одноосного
сжатия
;
σ
–
текущее
значение
прочности
.
На
рис
. 2.12,
а
,
б
приведены
такие
же
зависимости
,
полученные
Г
.
Т
.
Кир
-
ничанским
[5],
В
.
Т
.
Глушко
и
В
.
В
.
Виноградовым
[84]
и
А
.
Н
.
Ставрогиным
[4].
Анализ
приведенных
графиков
разупрочнения
и
разрыхления
показал
,
что
они
могут
быть
достаточно
близко
описаны
зависимостью
[117]
∗
−
=
−
−
v
v
ост
c
ост
R
R
R
ε
ε
σ
1
,
(2.1)
где
v
ε
–
текущее
значение
величины
объемного
разрыхления
.
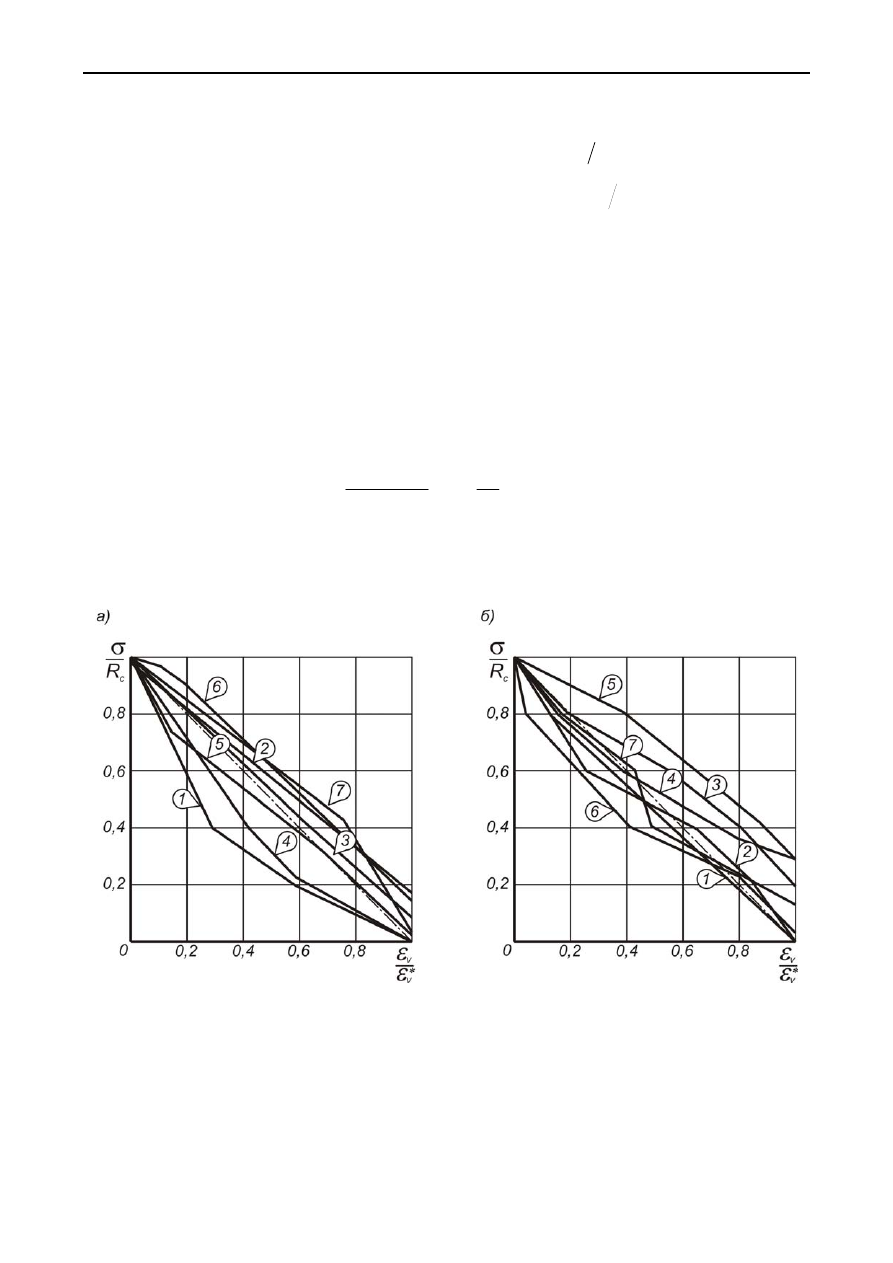
Рис
. 2.12.
Зависимость
относительной
прочности
образцов
углевмещающих
пород
от
величины
относительного
объемного
разрыхления
[84, 5]:
а
) 1-7
об
-
разцы
аргиллита
,
алевролита
,
песчаника
;
б
) 1 –
коелганский
мрамор
; 2 –
био
-
титовый
гранит
; 3 –
биотитовый
плагиогранит
; 4 –
песчаник
НВО
; 5 –
пла
-
гиогранит
; 6 –
диабаз
; 7 –
талькохлорит
З
АКОНОМЕРНОСТИ
РАЗРУШЕНИЯ
ГОРНЫХ
ПОРОД
ЗА
ПРЕДЕЛОМ
ПРОЧНОСТИ
43
Деформирование
произвольной
точки
породного
массива
в
окрестности
горной
выработки
происходит
аналогично
деформированию
породного
образца
в
режиме
контролируемого
нагружения
.
При
этом
роль
«
жесткого
»
пресса
вы
-
полняет
упруго
деформирующаяся
часть
породного
массива
.
Для
такой
модели
в
случае
плоской
деформации
зависимость
(2.1)
в
полярных
координатах
может
быть
представлена
в
следующей
форме
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
−
=
+
∗
ост
c
ост
v
r
R
R
R
σ
ε
ε
ε
θ
1
,
(2.2)
или
,
переходя
к
перемещениям
,
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
−
=
+
∗
ост
c
ост
v
R
R
R
r
U
dr
dU
σ
ε
1
.
(2.3)
Дифференциальное
уравнение
(2.3)
представляет
собой
физическое
урав
-
нение
состояния
,
которое
определяет
зависимость
между
радиальными
пере
-
мещениями
U
и
прочностью
породного
массива
на
расстоянии
r
от
центра
вы
-
работки
.
Значение
прочности
массива
на
одноосное
сжатие
( )
r
σ
в
процессе
де
-
формирования
породной
среды
изменяется
от
величины
c
R
на
границе
раздела
упругой
и
пластической
областей
до
величины
остаточной
прочности
ост
R
на
контуре
выработке
.
Закон
,
по
которому
происходит
это
изменение
,
может
быть
установлен
на
основе
гипотезы
о
сплошности
среды
в
окрестности
горной
вы
-
работки
.
2.3.
О
виде
функции
снижения
прочности
горных
пород
за
пределом
прочности
Существуют
разные
способы
учета
пластической
неоднородности
горных
пород
при
аналитическом
исследовании
упругопластического
состояния
по
-
родного
массива
.
Все
они
могут
быть
разделены
на
три
группы
.
Способы
первой
группы
основаны
на
суммировании
элементарных
актов
разрушения
:
чем
их
больше
,
тем
выше
степень
разупрочнения
.
При
этом
ис
-
Р
АЗДЕЛ
2
44
пользуют
либо
метод
Больцмана
с
привлечением
интегральных
уравнений
Вольтерра
,
либо
какой
-
нибудь
другой
вариант
последовательных
приближений
.
Другой
способ
учета
запредельного
деформирования
при
решении
задач
геомеханики
был
предложен
А
.
М
.
Линьковым
[118].
Он
заключается
в
том
,
что
совместно
решаются
уравнения
неразрывности
деформаций
и
равновесия
с
од
-
новременным
введением
экспериментально
установленной
зависимости
между
продольными
и
поперечными
относительными
деформациями
.
Известно
не
-
сколько
работ
,
в
которых
исследования
напряженно
-
деформированного
состоя
-
ния
вокруг
выработки
выполнены
подобным
образом
[119].
Более
простыми
являются
способы
третьей
группы
,
суть
которых
состоит
в
том
,
что
в
условие
прочности
вводится
некоторая
функция
снижения
прочности
( )
r
f
,
определяющая
закон
,
по
которому
изменяется
прочность
пород
на
одно
-
осное
сжатие
или
сцепление
в
окрестной
горной
выработки
в
зависимости
от
относительного
радиуса
r
(
0
R
R
r
=
,
где
0
R
–
радиус
выработки
;
R
–
текущий
радиус
).
М
.
Т
.
Алимжанов
приводит
самые
разные
аналитические
выражения
функ
-
ций
снижения
прочности
,
принадлежащие
различным
авторам
[120].
Принцип
выбора
аналитического
выражения
функции
снижения
прочности
по
сути
дела
один
.
Например
,
в
системе
координат
«
r
−
σ
»
экспериментальные
данные
апроксимируются
монотонной
кривой
,
ординаты
которой
увеличива
-
ются
от
некоторой
близкой
или
равной
нулю
величины
прочности
на
контуре
выработки
до
прочности
нетронутого
массива
c
R
на
границе
раздела
пластиче
-
ской
и
упругой
областей
.
В
той
или
иной
мере
известные
аналитические
выра
-
жения
функции
снижения
прочности
отвечают
этому
принципу
.
Но
совершенно
очевидно
,
что
если
при
построении
исходной
физической
модели
породная
среда
полагается
сплошной
,
то
и
вид
функции
( )
r
f
должен
соответствовать
этому
первоначальному
условию
.
В
частности
,
в
пластической
области
,
так
же
как
и
в
упругой
,
функция
напряжений
( )
r
F
должна
быть
бигармонической
,
то
-
гда
она
будет
иметь
единственное
конкретное
выражение
.