ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 1762
Скачиваний: 2
Р
АЗДЕЛ
5
120
асимметрию
и
эксцесс
.
С
учетом
соотношений
(5.39)
и
(5.34)
показатель
асим
-
метрии
можно
выразить
через
относительные
величины
:
(
)
3
2
2
2
3
2
1
)
1
(
2
3
−
+
−
=
A
A
A
β
.
Для
«
исправленного
»
ряда
,
в
который
внесены
элементы
с
макродефекта
-
ми
,
получим
2
2
1
2
2
1
2
1
2
2
/
2
A
K
K
m
K
m
K
A
=
=
;
3
3
1
3
2
1
3
1
2
3
/
3
A
K
K
m
K
m
K
A
=
=
;
4
4
1
4
2
1
2
1
2
2
/
4
A
K
K
m
K
m
K
A
=
=
.
Тогда
показатель
асимметрии
примет
вид
:
3
2
2
1
2
2
2
2
1
2
3
3
1
3
/
2
1
1
2
3
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
=
A
K
K
A
K
K
A
K
K
β
.
(5.47)
Аналогично
получим
выражение
для
показателя
эксцесса
:
2
2
2
1
2
2
2
1
2
3
3
1
3
4
4
1
4
/
2
1
3
6
4
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
+
−
=
A
K
K
A
K
K
A
K
K
A
K
K
β
.
(5.48)
Если
исходное
распределение
симметрично
,
то
с
учетом
(5.43)
и
(5.45)
по
-
лучим
,
что
показатели
асимметрии
и
эксцесса
«
исправленного
»
ряда
зависят
только
от
относительной
величины
2
A
,
которая
связана
с
вариацией
значений
случайной
величины
(
1
2
2
+
=
η
A
).
Исследуем
,
как
влияет
наличие
макродефектов
на
закон
распределения
прочности
структурных
элементов
массива
.
Как
и
в
предыдущей
задаче
для
простоты
изложения
будем
полагать
,
что
прочность
дефектных
элементов
близка
нулю
.
В
этом
случае
коэффициент
влияния
трещин
определяется
фор
-
мулой
(5.32).
Определим
для
рассмотренного
выше
примера
(
1
1
=
m
,
2
,
1
1
2
2
=
+
=
η
A
)
моменты
«
исправленного
»
ряда
по
формулам
(5.46)
для
различных
значений
О
ПРЕДЕЛЕНИЕ
КОЭФФИЦИЕНТА
СТРУКТУРНОГО
ОСЛАБЛЕНИЯ
НА
ОСНОВЕ
ВЕРОЯТНОСТНО
-
СТАТИСТИЧЕСКИХ
МОДЕЛЕЙ
121
расстояния
между
трещинами
и
подсчитаем
соответствующие
коэффициенты
асимметрии
и
эксцесса
(
табл
. 5.5).
Таблица
5.5
Значения
«
исправленных
»
показателей
асимметрии
и
эксцесса
для
исходного
распределения
с
параметром
2
A
=1,2
0
l
l
m
ν
′
2
1
β
′
2
β
1,0
1,5
2,0
2,5
3,0
10,0
0,50
0,60
0,66
0,71
0,75
0,90
1,33
0,76
0,50
0,36
0,27
0,09
4,11
3,46
3,19
3,05
2,92
2,97
Из
таблицы
видно
,
что
с
уменьшением
расстояния
между
трещинами
m
l
,
т
.
е
.
с
ростом
интенсивности
трещин
,
значения
асимметрии
и
эксцесса
увеличи
-
ваются
.
Точки
с
координатами
(
′
′
2
2
1
,
β
β
),
нанесенные
на
график
Пирсона
,
с
увеличением
плотности
трещин
все
более
удаляются
от
точки
,
соответствую
-
щей
нормальному
закону
(
рис
. 5.9).
Траектория
движения
точки
для
заданного
значения
2
,
1
2
=
A
проходит
вблизи
линий
,
соответствующих
гамма
-
распределению
и
распределению
Вейбулла
.
При
других
сочетаниях
моментов
симметричного
распределения
(
например
,
при
3
,
1
2
=
A
)
значения
асимметрии
и
эксцесса
таковы
,
что
движение
точки
осуществляется
вблизи
линии
логариф
-
мически
нормального
распределения
(
табл
. 5.6).
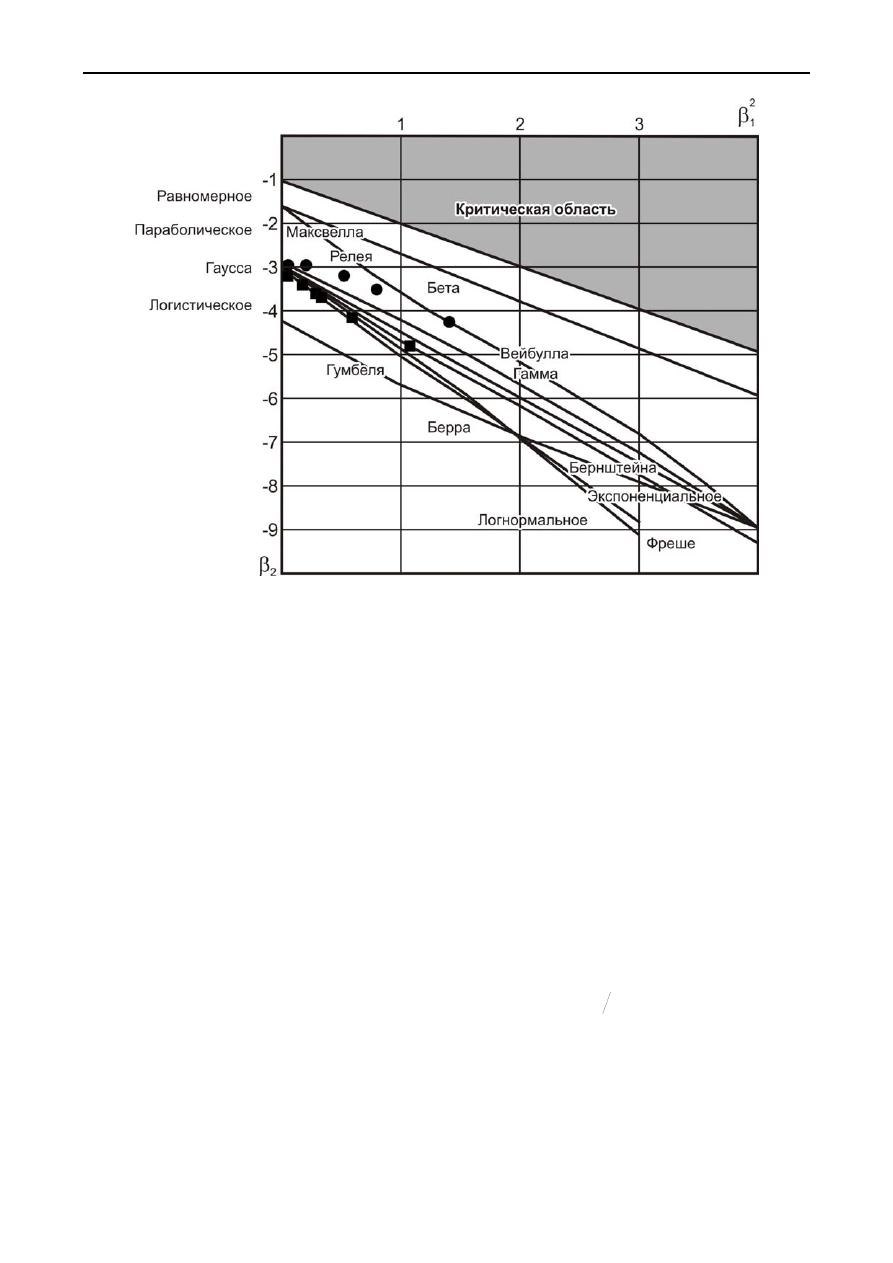
Р
АЗДЕЛ
5
122
Рис
. 5.9.
Диаграмма
Пирсона
с
точками
для
статистических
распределений
,
в
которые
условно
внесены
элементы
с
макродефектами
:
●
–
точки
,
соответ
-
ствующие
исходному
ряду
с
соотношением
начальных
моментов
2
A =1,2;
■
–
точки
,
соответствующие
исходному
ряду
с
соотношением
начальных
момен
-
тов
2
A =1,3
Искусственное
внесение
элементов
с
нулевой
прочностью
в
статистиче
-
ский
ряд
меняет
значения
асимметрии
и
эксцесса
,
а
,
следовательно
,
и
вид
рас
-
пределения
.
Из
рис
. 5.9
видно
,
что
с
уменьшением
расстояния
между
трещина
-
ми
отклонение
от
симметричного
распределения
становится
все
более
значи
-
тельным
.
Формально
,
для
приведенного
примера
при
1
)
(
0
<
l
l
m
распределение
становится
близким
к
экспоненциальному
закону
.
Однако
это
противоречит
физической
сути
задачи
,
свидетельствуя
о
глубоких
качественных
изменениях
в
среде
,
где
элементы
с
нулевой
прочностью
становятся
преобладающими
,
а
сама
среда
по
своим
свойствам
приближается
к
однородной
сыпучей
.
Очевидно
,
что
О
ПРЕДЕЛЕНИЕ
КОЭФФИЦИЕНТА
СТРУКТУРНОГО
ОСЛАБЛЕНИЯ
НА
ОСНОВЕ
ВЕРОЯТНОСТНО
-
СТАТИСТИЧЕСКИХ
МОДЕЛЕЙ
123
если
полагать
прочность
дефектных
элементов
равной
нулю
,
случай
1
)
(
0
<
l
l
m
следует
исключить
из
рассмотрения
.
Таблица
5.6
Значения
«
исправленных
»
показателей
асимметрии
и
эксцесса
для
исходного
распределения
с
параметром
2
A
=1,3
0
l
l
m
ν
′
2
1
β
′
2
β
1,0
1,5
2
2,5
3
10
0,5
0,6
0,66
0,71
0,75
0,9
1,15
0,65
0,42
0,30
0,22
0,03
4,83
4,05
3,69
3,50
3,38
3,05
Таким
образом
,
наличие
трещин
в
реальном
породном
массиве
не
только
оказывает
влияние
на
статистические
оценки
исследуемого
количественного
признака
,
но
и
меняет
закон
распределения
вероятностей
всех
его
механиче
-
ских
параметров
.
Вид
«
исправленного
»
распределения
зависит
от
соотношений
начальных
моментов
исходного
статистического
распределения
,
полученного
как
результат
опробования
ненарушенных
структурных
элементов
.
Степень
от
-
клонения
прочности
элементов
от
симметричного
распределения
определяется
расстоянием
между
трещинами
.
Исследуем
теперь
,
как
повлияет
на
это
откло
-
нение
угол
наклона
трещин
к
оси
нагружения
.
5.3.
Исследование
влияния
параметров
трещиноватости
на
вид
рас
-
пределения
прочности
структурных
элементов
5.3.1.
Исследование
влияния
угла
наклона
трещин
Приведенные
выше
результаты
получены
в
предположении
,
что
прочность
дефектных
образцов
породы
(
структурных
элементов
массива
)
близка
нулю
.
Р
АЗДЕЛ
5
124
Между
тем
,
и
имеющиеся
в
литературе
данные
,
и
результаты
экспериментов
,
описанных
в
п
. 5.2,
говорят
о
том
,
что
образец
,
нарушенный
трещинами
,
час
-
тично
сохраняет
свою
несущую
способность
,
что
можно
охарактеризовать
функцией
снижения
прочности
( )
( )
α
α
c
R
q
f
=
,
равной
отношению
разрушаю
-
щей
нагрузки
к
пределу
прочности
на
сжатие
монолитного
образца
,
не
нару
-
шенного
макротрещинами
.
Эта
функция
может
быть
получена
на
основе
обра
-
ботки
результатов
наблюдений
.
Однако
,
экспериментальные
данные
в
силу
погрешностей
измерительных
приборов
,
несовершенства
технологии
изготовления
образцов
и
условий
за
-
щемления
на
их
торцах
,
а
также
в
силу
других
причин
,
являются
величинами
случайными
.
Для
получения
их
оценок
с
высокой
достоверностью
требуется
большое
количество
опытов
,
проведение
которых
в
лабораторных
условиях
достаточно
трудоемко
.
Указанных
недостатков
физического
моделирования
лишено
математическое
моделирование
.
Последнее
,
хотя
и
предполагает
из
-
вестную
идеализацию
объекта
,
позволяет
исключить
влияние
случайных
мало
-
значимых
факторов
и
получить
количественные
оценки
изучаемого
процесса
,
обусловленные
действием
тех
фундаментальных
законов
,
которые
положены
в
основу
математической
модели
.
Поэтому
влияние
ориентации
плоскостей
ос
-
лабления
на
процесс
разрушения
структурного
элемента
массива
исследовался
путем
математического
моделирования
.
Структурный
элемент
массива
можно
представить
как
квадратный
блок
,
весом
которого
можно
пренебречь
,
покоящийся
на
поверхности
полуплоскости
.
Блок
пересекает
трещина
,
расположенная
под
углом
α
к
горизонтальной
оси
.
Задача
моделируется
путем
погружения
системы
в
неограниченную
упругую
плоскость
.
Решение
выполнялось
методом
граничных
элементов
[
234
]
.
Оконту
-
ривание
блока
и
части
полуплоскости
,
имитирующей
основание
,
на
котором
находится
блок
,
т
.
е
.
выделение
их
из
бесконечной
среды
,
осуществлялось
гра
-
ничными
элементами
в
рамках
метода
разрывных
смещений
.