ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 1757
Скачиваний: 2
Р
АЗДЕЛ
5
130
Видно
,
что
при
сохра
-
нении
нарушенными
эле
-
ментами
частичной
несу
-
щей
способности
вариация
прочности
не
так
велика
,
как
в
случае
полного
раз
-
рушения
дефектных
эле
-
ментов
(
см
.
рис
.5.8).
Определим
централь
-
ные
моменты
(5.46)
и
свя
-
занные
с
ними
показатели
асимметрии
и
эксцесса
учитывая
,
что
элементы
,
нарушенные
трещиной
,
сохраняют
некоторую
не
-
сущую
способность
.
В
этом
случае
коэффициенты
влияния
трещин
опреде
-
ляются
формулой
(5.31),
где
)
(
α
f
=
( )
α
c
R
q
и
опре
-
деляется
формулой
(5.49).
В
качестве
примера
рассмотрим
ранее
исследо
-
ванный
исходный
ряд
с
со
-
отношением
моментов
:
3
,
1
2
=
A
.
Предположение
о
том
,
что
дефектные
элементы
частично
сохраняют
несущую
способность
,
влия
-
ет
на
величины
асимметрии
и
эксцесса
.
В
наибольшей
степени
структурный
элемент
ослабляет
кососекущая
трещина
,
составляющая
с
горизонтальной
гра
-
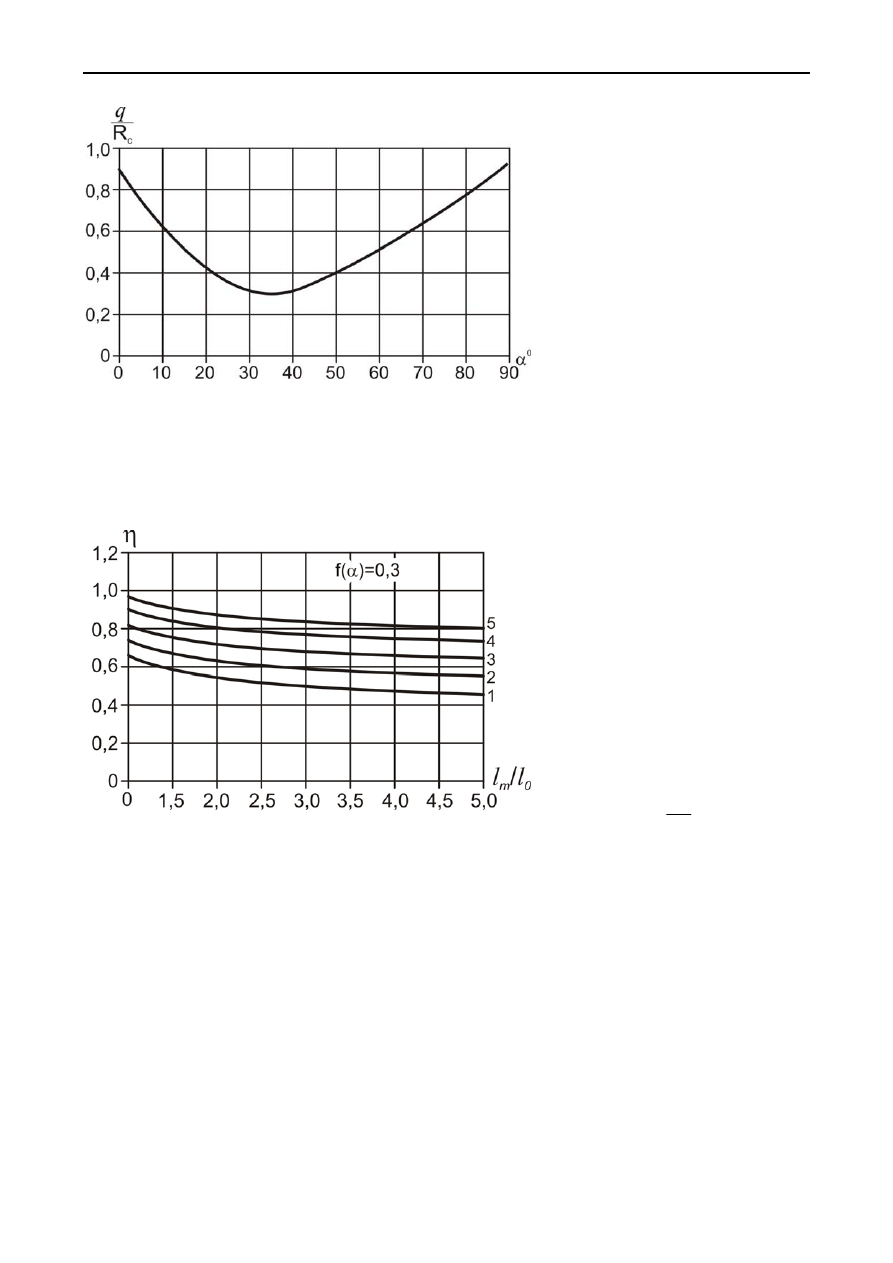
Рис
. 5.13.
Зависимость
разрушающей
нагрузки
от
угла
наклона
трещины
Рис
. 5.14.
Зависимость
вариации
прочности
массива
от
расстояния
между
трещинами
в
предположении
,
что
дефектные
элементы
час
-
тично
сохраняют
несущую
способность
: 1,2, 3,
4, 5 –
при
1
2
2
+
=
η
A
= 1,1; 1,2; 1,3; 1,4; 1,5
со
-
ответственно
О
ПРЕДЕЛЕНИЕ
КОЭФФИЦИЕНТА
СТРУКТУРНОГО
ОСЛАБЛЕНИЯ
НА
ОСНОВЕ
ВЕРОЯТНОСТНО
-
СТАТИСТИЧЕСКИХ
МОДЕЛЕЙ
131
нью
элемента
углы
30-45
0
(
)
(
α
f
=0,3).
Для
такого
значения
функции
снижения
прочности
асимметрия
и
эксцесс
распределения
также
значительно
откланяют
-
ся
от
характеристик
нормального
закона
,
как
и
при
расчете
моментов
в
предпо
-
ложении
,
что
прочность
дефектных
элементов
равна
нулю
(
рис
. 5.15).
Рис
. 5.15.
Зависимость
показателей
асимметрии
2
1
β
(
а
)
и
эксцесса
2
β
(
б
)
от
расстояния
между
трещинами
при
частичном
сохранении
образцами
несущей
способности
: 1, 2, 3 –
)
(
α
f
=0; 0,3; 0,4
соответственно
Особенно
существенно
это
отклонение
при
значениях
1
)
(
0
≈
l
l
m
.
С
уве
-
личением
)
(
α
f
,
т
.
е
.
при
положении
трещин
,
близком
к
нормальносекущему
,
отклонение
от
симметричного
распределения
уменьшается
.
Все
рассуждения
,
приведенные
выше
,
выполнены
в
предположении
,
что
для
генеральной
совокупности
известно
расстояние
между
прирожденными
трещинами
.
Между
тем
имеющиеся
в
литературе
сведения
о
значениях
этой
ве
-
личины
свидетельствуют
о
ее
значительной
изменчивости
.
Расстояние
между
трещинами
следует
рассматривать
как
случайную
величину
и
при
оценке
проч
-
ности
массива
учитывать
не
только
ее
математическое
ожидание
,
но
и
возмож
-
ный
разброс
значений
относительно
среднего
.
Р
АЗДЕЛ
5
132
5.3.2.
Исследование
влияния
изменчивости
расстояния
между
трещи
-
нами
на
вид
распределения
прочности
структурных
элементов
В
математическом
отношении
трещина
представляет
собой
поверхность
раздела
,
по
которой
претерпевает
разрыв
вектор
смещений
.
След
этой
поверх
-
ности
на
плоскости
–
прямая
L
,
с
общим
уравнением
Ax + By + C = 0,
где
A, B
–
координаты
нормального
вектора
прямой
.
Разделив
обе
его
части
на
нормирующий
множитель
2
2
B
A
+
,
получим
нормальное
уравнение
прямой
0
sin
cos
=
−
+
l
y
x
α
α
,
где
2
2
cos
B
A
A
+
=
α
,
2
2
sin
B
A
B
+
=
α
–
направляющие
косинусы
прямой
,
l
–
расстояние
от
прямой
до
начала
координат
.
Если
через
начало
координат
про
-
вести
прямую
,
параллельную
прямой
L
,
то
l
будет
равно
расстоянию
между
прямыми
.
Таким
образом
,
уравнение
0
sin
cos
=
−
+
nl
y
x
α
α
,
n
= 0, 1, 2,…..,
где
l
–
расстояние
между
трещинами
,
определяет
сис
-
тему
трещин
на
плоскости
(
рис
. 5.16).
М
.
В
.
Гзовский
[236]
предлагал
при
изучении
тектонических
разрывов
использовать
современные
знания
о
физических
усло
-
виях
их
возникновения
.
В
частности
,
закономерности
возникновения
элементар
-
Рис
. 5.16.
К
определению
расстояния
между
трещинами
на
плоскости
О
ПРЕДЕЛЕНИЕ
КОЭФФИЦИЕНТА
СТРУКТУРНОГО
ОСЛАБЛЕНИЯ
НА
ОСНОВЕ
ВЕРОЯТНОСТНО
-
СТАТИСТИЧЕСКИХ
МОДЕЛЕЙ
133
ных
поверхностей
механического
разрушения
нужно
рассматривать
с
учетом
того
,
что
процесс
разрушения
развивается
длительно
и
непрерывно
совместно
с
упругим
и
пластическим
деформированием
,
параллельно
с
процессом
залечи
-
вания
разрывов
.
Важным
следствием
образования
тектонического
разрыва
яв
-
ляется
изменение
первичного
напряженного
состояния
вблизи
него
.
Отсюда
следует
,
что
место
положения
каждой
трещины
определенного
порядка
зависит
от
положения
смежных
с
ней
трещин
.
Особого
внимания
в
этой
связи
заслуживает
подход
,
основанный
на
при
-
менении
законов
фрактальной
геометрии
.
Он
предполагает
оценку
исследуемо
-
го
объекта
на
основе
рассмотрения
его
как
совокупности
самоподобных
мно
-
жеств
,
организация
которых
зависит
как
от
детерминированных
,
так
и
от
слу
-
чайных
факторов
.
Таким
образом
,
расстояние
между
трещинами
является
основным
пара
-
метром
трещиноватости
.
Эта
величина
формировалась
под
воздействием
боль
-
шого
числа
случайных
событий
и
сама
является
случайной
.
Но
как
результат
проявления
массовых
случайных
событий
подчиняется
определенному
закону
распределения
вероятностей
.
Большой
объем
статистической
информации
о
величине
расстояний
между
трещинами
был
собран
С
.
А
.
Батугиным
[237].
Для
построения
эмпирических
распределений
результаты
измерений
отбирались
на
однородных
по
трещино
-
ватости
участках
на
горнодобывающих
предприятиях
Кузбасса
.
Из
рис
. 5.17
видно
,
что
распределение
случайной
величины
имеет
асимметричный
характер
.
Автор
отмечает
,
что
по
критерию
Пирсона
при
5%
уровне
значимости
не
отвер
-
гаются
несколько
статистических
гипотез
(
что
характерно
для
выборок
не
-
большого
объема
).
Однако
,
исходя
из
физической
природы
данной
случайной
величины
,
следует
в
качестве
вероятностной
модели
распределения
расстояния
между
трещинами
принять
закон
Релея
.
Действительно
,
закон
Релея
выведен
как
статистическая
модель
расстоя
-
ния
между
двумя
точками
плоскости
.
Если
X
и
Y
–
нормальные
независимые
Р
АЗДЕЛ
5
134
случайные
величины
с
нулевыми
математическими
ожиданиями
и
равными
среднеквадратическими
отклонениями
σ
,
то
величина
2
2
Y
X
l
+
=
распределена
по
закону
Релея
с
плотностью
[210]:
( )
.
0
,
0
,
0
0
2
exp
,
2
2
<
>
≥
⎪
⎩
⎪
⎨
⎧
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
x
x
x
x
x
f
σ
σ
σ
σ
(5.50)
Рис
. 5.17.
Распределение
расстояний
между
трещинами
в
породах
Таштогольского
железорудного
месторождения
[113]
Это
распределение
содержит
только
параметр
масштаба
σ
,
с
которым
ма
-
тематическое
ожидание
m
связано
очень
простой
зависимостью
m
52
,
0
=
σ
.
(5.51)
По
данным
С
.
А
.
Батугина
,
для
обследованных
им
типов
пород
(
песчани
-
ков
,
сланцев
)
характерна
относительная
вариация
расстояний
между
трещина
-