ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 1756
Скачиваний: 2
О
ПРЕДЕЛЕНИЕ
КОЭФФИЦИЕНТА
СТРУКТУРНОГО
ОСЛАБЛЕНИЯ
НА
ОСНОВЕ
ВЕРОЯТНОСТНО
-
СТАТИСТИЧЕСКИХ
МОДЕЛЕЙ
125
Решение
выполнялось
при
следующих
граничных
условиях
:
на
боковых
гранях
блока
равны
нулю
нормальные
напряжения
,
на
верхней
грани
блока
за
-
дана
равномерно
распределенная
нагрузка
интенсивностью
q
,
такая
же
нагруз
-
ка
с
противоположным
знаком
задана
на
нижней
грани
.
Кроме
того
,
на
нижней
и
верхней
гранях
равны
нулю
горизонтальные
перемещения
(
рис
. 5.10).
Рис
. 5.10.
Расчетная
схема
задачи
:
а
)
физическая
модель
;
б
)
гранично
-
элементная
модель
Состояние
блока
как
структурного
элемента
массива
оценивается
величи
-
ной
условных
зон
разрушения
,
под
которыми
понимается
совокупность
точек
,
в
которых
не
выполняются
предельные
соотношения
между
компонентами
тен
-
зора
напряжений
в
соответствии
с
принятым
критерием
прочности
.
Условие
разрушения
для
горных
пород
,
неодинаково
сопротивляющихся
растяжению
и
сжатию
,
достаточно
хорошо
описывается
критерием
прочности
(3.8),
получен
-
ным
в
разделе
3.
Появление
отдельных
точек
,
в
которых
выполняется
данное
условие
раз
-
рушения
,
еще
не
свидетельствует
о
разрушении
блока
как
структурного
эле
-
мента
массива
.
Если
же
такими
точками
охвачена
область
,
сопоставимая
с
раз
-
мерами
самого
блока
,
можно
утверждать
,
что
материал
его
претерпевает
необ
-
Р
АЗДЕЛ
5
126
ратимые
деформации
и
структурный
элемент
теряет
способность
сопротив
-
ляться
нагрузке
.
При
моделировании
процесса
разрушения
вертикальная
нагрузка
задава
-
лась
в
долях
от
предполагаемого
предела
прочности
материала
блока
на
одно
-
осное
сжатие
.
На
каждом
этапе
нагружения
выполнялась
оценка
напряженно
-
деформированного
состояния
блока
в
соответствии
с
выбранной
теорией
проч
-
ности
,
и
определялся
уровень
разрушающей
нагрузки
,
вызывающей
переход
материала
блока
в
стадию
неупругого
деформирования
.
Предполагалось
,
что
характер
распространения
условных
зон
разрушения
связан
с
поведением
ос
-
лабляющего
элемента
–
трещины
.
В
вычислительной
процедуре
трещина
может
моделироваться
и
как
«
зияющая
»,
нарушающая
сплошность
,
с
помощью
эле
-
ментов
разрывных
смещений
,
и
как
заполненная
достаточно
связным
материа
-
лом
,
способным
к
упругим
деформациям
.
Тогда
заполненная
трещина
может
моделироваться
как
упругий
контакт
специальными
контактными
(
пластовыми
)
элементами
.
В
реальных
условиях
трещины
,
как
правило
,
заполнены
глинистым
мате
-
риалом
,
обладающим
гораздо
меньшим
сцеплением
,
чем
горная
порода
.
Под
действием
внешних
сил
по
поверхностям
ослабления
может
происходить
скольжение
частей
массива
относительно
друг
друга
или
разрыв
сплошности
.
Математическая
модель
деформирования
структурного
элемента
,
содержащего
трещину
,
должна
отражать
возможность
неупругого
деформирования
материа
-
ла
–
заполнителя
трещины
,
то
есть
содержать
ограничивающее
соотношение
между
нормальными
и
касательными
напряжениями
,
передающимися
через
контакт
.
В
качестве
такого
соотношения
удобнее
всего
использовать
условие
Кулона
–
Мора
:
ρ
σ
τ
tg
c
n
+
=
.
Здесь
τ
–
напряжение
сдвига
,
n
σ
–
нормальное
напряжение
,
ρ
и
с
–
соот
-
ветственно
угол
внутреннего
трения
и
сцепления
материала
-
заполнителя
тре
-
О
ПРЕДЕЛЕНИЕ
КОЭФФИЦИЕНТА
СТРУКТУРНОГО
ОСЛАБЛЕНИЯ
НА
ОСНОВЕ
ВЕРОЯТНОСТНО
-
СТАТИСТИЧЕСКИХ
МОДЕЛЕЙ
127
щин
.
В
[
234
]
подробно
описана
вычислительная
процедура
,
учитывающая
скольжение
вдоль
трещины
и
раскрытие
контакта
.
В
данной
задаче
каждая
грань
блока
представлена
10-
ю
граничными
эле
-
ментами
разрывных
смещений
.
Трещина
с
углом
наклона
α
к
горизонтальной
оси
моделировалась
14-
ю
контактными
элементами
,
допускающими
неупругие
деформации
.
Грани
блока
полагались
единичной
длины
,
вертикальная
нагрузка
q
задавалась
в
долях
от
предела
прочности
на
сжатие
R
c
.
Модуль
упругости
E
составлял
105
единиц
напряжений
,
коэффициент
Пуассона
μ
=0,2,
нормальная
и
касательная
жесткости
упругого
контакта
выбирались
из
расчета
,
что
ширина
трещины
составляет
10
-6
единиц
длины
.
Характеристики
материала
трещины
принимались
равными
:
с
=0,
ρ
=30
0
.
Вычислительный
экспе
-
римент
начинался
с
моделиро
-
вания
монолитного
образца
(
блока
),
не
ослабленного
тре
-
щиной
,
с
целью
подтверждения
правильности
постановки
зада
-
чи
и
разработанного
алгоритма
.
Характер
расположения
точек
,
напряжения
в
которых
не
удов
-
летворяют
условию
прочности
,
совпадает
с
представлениями
о
разрушении
твердого
тела
в
со
-
ответствии
с
теорией
Кулона
–
Мора
.
Из
рис
. 5.11
видно
,
что
совокупности
этих
точек
образуют
линии
,
ориен
-
тированные
к
направлению
приложения
нагрузки
под
углом
,
близким
к
±
40
0
.
В
главе
3
показана
связь
между
параметрами
криволинейной
огибающей
пре
-
дельных
кругов
Мора
и
прямолинейной
,
что
позволяет
определить
угол
внут
-
Рис
. 5.11.
Характер
расположения
точек
разрушения
при
c
R
q
=
в
отсутствие
трещины
Р
АЗДЕЛ
5
128
реннего трения в зависимости от коэффициента хрупкости пород
, и величи-
ны нормальной составляющей напряжения
:
1
2
2
1
*
c
R
arctg
.
При
=0.1 и
c
R
q
величина параметра огибающей кругов Мора
*
бу-
дет равна 18
0
. Тогда площадки скольжения составят с направлением наиболь-
шего главного напряжения углы:
2
45
*
0
= 36
0
,
что совпадает с полученной картиной напряженного состояния блока.
Дальнейшие расчеты связаны с моделированием трещин под различными
углами
к горизонтальной оси. При
=30
0
точки разрушения появляются уже
при нагрузке, составляющей 0,3
R
c
, распространяясь от краевых частей блока к
его центру. Приращение нагрузки на величину 0,05
R
c
, то есть увеличение ее до
значения
q
=0,35
R
c
вызывает рост области неупругих деформаций до размеров,
сопоставимых с размерами блока. Эту стадию будем характеризовать как не-
способность структурного элемента далее воспринимать нагрузку.
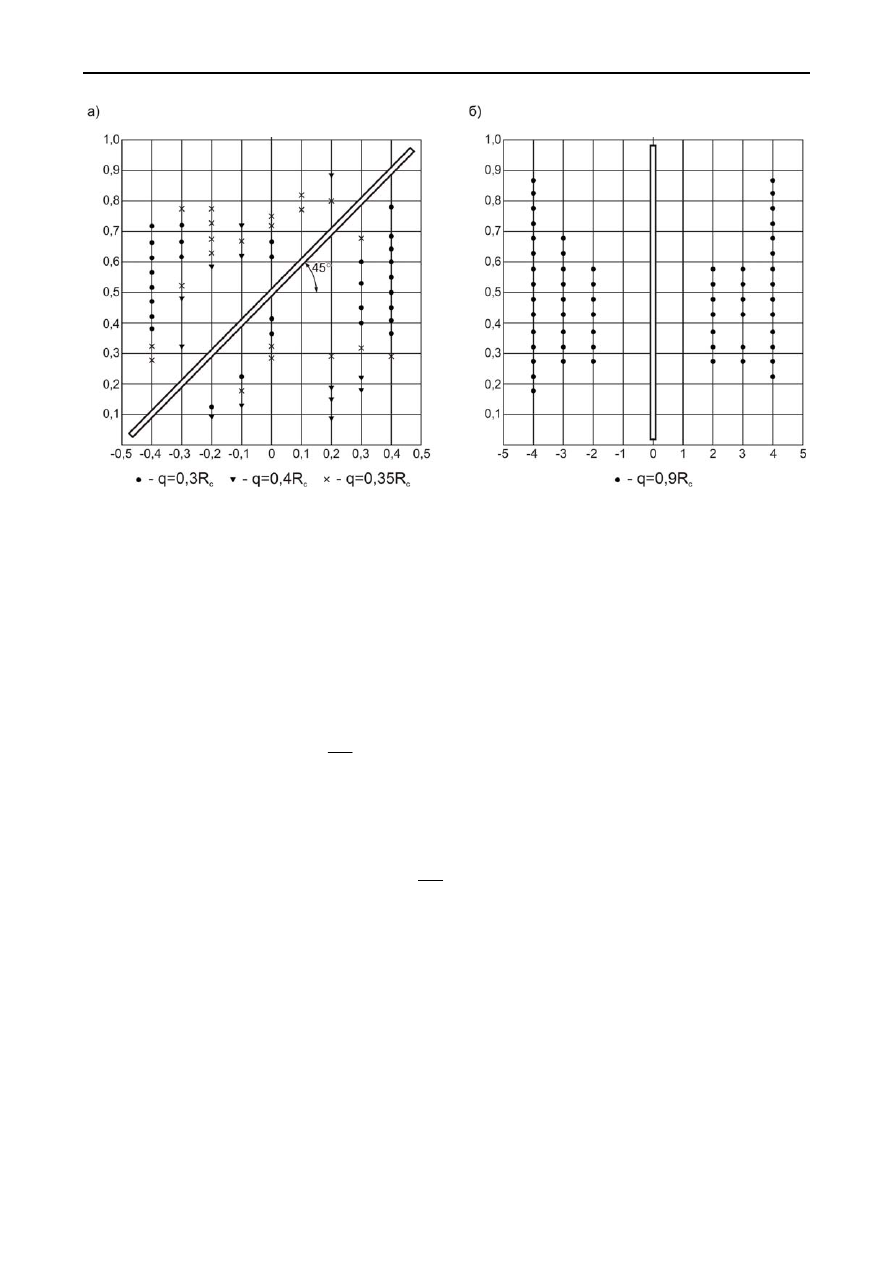
Характер расположения точек разрушения показан на рис. 5.12 для вариан-
тов расчета, выполненного при
, равном 45
0
и 90
0
.
Трещина, расположенная под углом
=45
0
, ослабляет структурный эле-
мент в столь же значительной мере. Первые неупругие деформации появляются
при
q
=0,35
R
c
, при
q
=0,4
R
c
структурный элемент в большей своей части охва-
чен зоной разрушения. Трещины, расположенные под углами, близкими к 0
0
и
90
0
оказывают на прочность элемента гораздо меньшее влияние. Нормальносе-
кущая трещина, т. е расположенная под углом
=90
0
, снижает значение разру-
шающей нагрузки до величины
q
=0,85
R
c
.
О
ПРЕДЕЛЕНИЕ
КОЭФФИЦИЕНТА
СТРУКТУРНОГО
ОСЛАБЛЕНИЯ
НА
ОСНОВЕ
ВЕРОЯТНОСТНО
-
СТАТИСТИЧЕСКИХ
МОДЕЛЕЙ
129
Рис
. 5.12
Характер
расположения
точек
разрушения
в
образце
:
а
)
α
=45
0
;
б
)
α
=90
0
Кривую
на
рис
. 5.13,
характеризующую
снижение
прочности
структурного
элемента
в
зависимости
от
угла
наклона
плоскости
ослабления
,
можно
аппрок
-
симировать
параболической
зависимостью
вида
:
( )
9359
,
0
0386
,
0
10
7
2
4
+
−
⋅
=
−
α
α
α
c
R
q
(5.49)
Функция
(5.49)
имеет
явно
выраженный
минимум
при
α
=35
0
.
Функция
снижения
прочности
( )
α
c
R
q
характеризует
собой
закономерные
изменения
прочности
структурных
элементов
в
зависимости
от
ориентации
трещин
.
Используем
полученную
зависимость
для
моделирования
статистиче
-
ской
совокупности
,
содержащей
дефектные
элементы
,
нарушенные
трещинами
.
Относительная
вариация
прочности
в
данном
случае
определяется
по
формуле
(5.38)
с
учетом
зависимости
(5.49).
На
рис
. 5.14
приведена
зависимость
относительной
вариации
прочности
структурных
элементов
от
расстояния
между
трещинам
при
)
(
α
f
=0,3.