ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 1753
Скачиваний: 2
Р
АЗДЕЛ
6
150
точно
по
логнормальному
закону
распределения
.
Для
трехпараметрических
логнормальных
распределений
отношение
этих
случайных
величин
будет
рас
-
пределено
только
приближенно
логнормально
.
Оказывается
,
если
не
налагать
на
рассматриваемые
случайные
величины
жестких
требований
,
а
потребовать
только
их
представимости
в
виде
произведения
достаточно
большого
числа
со
-
множителей
,
то
в
пределе
(
по
закону
больших
чисел
)
для
отношения
таких
слу
-
чайных
величин
получим
асимптотически
логарифмически
нормальное
распре
-
деление
[241].
Наличие
таких
свойств
у
логнормального
распределения
позво
-
ляет
его
эффективно
использовать
в
тех
задачах
надежности
,
где
приходится
оперировать
с
отношениями
случайных
величин
,
для
которых
отсутствует
ин
-
формация
об
их
функциях
распределения
.
Исходя
из
изложенного
выше
,
определим
коэффициент
структурного
ос
-
лабления
на
основе
гипотезы
о
логарифмически
нормальном
распределении
прочности
структурных
элементов
породного
массива
.
6.2.
Определение
коэффициента
структурного
ослабления
на
основе
гипотезы
о
логарифмически
нормальном
распределении
прочности
струк
-
турных
элементов
породного
массива
Предположим
,
что
минимальное
значение
прочности
R
структурных
эле
-
ментов
рассматриваемой
стохастической
системы
стремится
к
нулю
и
будем
рассматривать
двухпараметрическое
логнормальное
распределение
.
Такое
предположение
идет
в
запас
прочности
.
Как
указывалось
выше
,
логарифмически
нормальное
распределение
опи
-
сывает
случайную
величину
,
логарифм
которой
распределен
по
нормальному
закону
с
параметрами
a
и
σ
,
т
.
е
.
плотность
распределения
случайной
величи
-
ны
R
z
ln
=
имеет
вид
(6.6).
Вероятность
того
,
что
случайная
величина
z
не
окажется
ниже
некоторого
предельного
значения
z
m
,
равна
(
)
(
)
[
]
σ
/
1
a
z
F
z
z
p
m
m
−
−
=
∞
p
p
.
В
ЕРОЯТНОСТНО
-
СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЧНОСТИ ПОРОДНОГО МАССИВА С УЧЕТОМ МАКРОДЕФЕКТОВ
151
Здесь функция
F(z)
определяется относительно переменной
z=lnR
в соот-
ветствии с (5.7). Разрешим это уравнение относительно
z
m
:
p
F
a
z
m
1
arg
0
.
Возвращаясь к случайной величине
R
, получим выражение для прочности
массива:
)
1
arg
exp(
0
p
F
a
R
m
.
(6.16)
Коэффициент структурного ослабления, также как и во всех предыдущих
случаях, выразим через относительную вариацию прочности структурных
элементов
. Разделив обе части (6.16) на величину математического ожидания
m
1
, получим:
)
2
1
arg
exp(
2
0
p
F
k
c
.
Учитывая, что
2
2
exp
1
, получим окончательно
1
)
1
ln
1
exp(arg
2
2
0
p
F
k
c
.
(6.17)
Исследуем полученную зависимость. При
=0, т.е. при идеально однород-
ной среде, коэффициент структурного ослабления равен единице, и прочность
массива совпадает с прочностью его структурных элементов (образцов). С уве-
личением коэффициента вариации, т.е. с ростом степени неоднородности сре-
ды, коэффициент структурного ослабления уменьшается, уменьшая тем самым
прочность массива. При
функция (6.17) асимптотически приближается к
нулю. Данные соотношения, а также характер изменения зависимости (6.17)
(рис. 6.2) вполне соответствуют физической сути коэффициента структурного
ослабления.
Р
АЗДЕЛ
6
152
Количественная
оценка
отличия
прочности
массива
от
средней
прочности
породных
образцов
–
коэффициент
струк
-
турного
ослабления
c
k
–
выра
-
жена
через
относительную
ва
-
риацию
прочности
структур
-
ных
элементов
массива
(
пород
-
ных
образцов
)
η
,
отражающую
степень
неоднородности
среды
на
микроуровне
.
Неоднород
-
ность
,
обусловленная
наличием
макродефектов
,
в
частности
систем
трещин
,
должна
быть
учтена
путем
введения
в
рас
-
четную
формулу
(6.17) «
ис
-
правленной
»
вариации
/
η
,
определяемой
в
зависимости
от
расстояния
между
трещинами
и
угла
их
падения
по
формулам
(6.1).
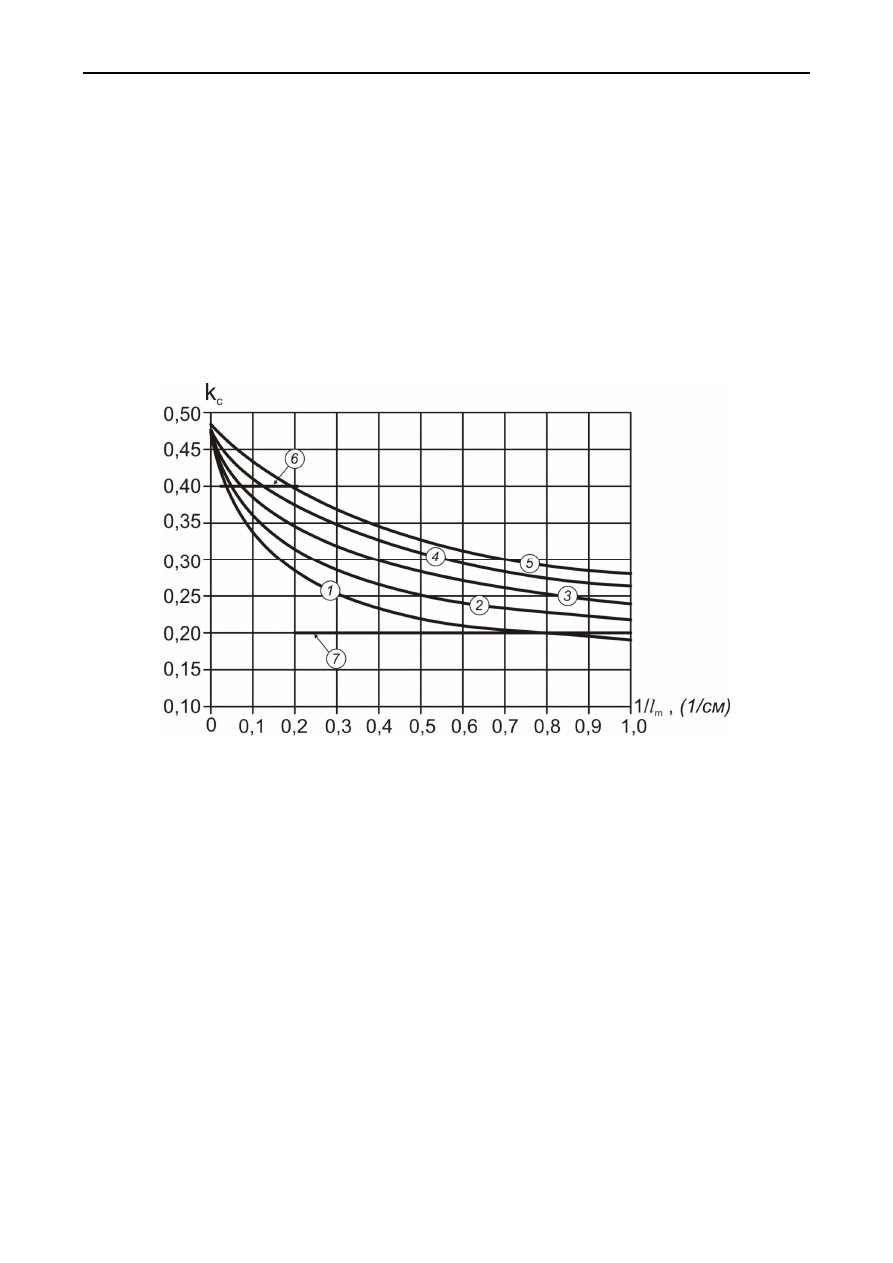
На
рис
. 6.3
показана
зависимость
коэффициента
структурного
ослабления
от
расстояния
между
трещинами
и
угла
падения
основной
системы
трещин
.
Там
же
показано
(
горизонтальные
линии
),
насколько
близко
соответствуют
значения
коэффициента
структурного
ослабления
,
рекомендуемые
в
СНиП
-II-
94-80 [219],
вычисленным
по
предлагаемым
зависимостям
.
Совпадение
доста
-
точно
близкое
,
с
той
разницей
,
что
формула
(6.17)
позволяет
для
конкретных
горно
-
геологических
условий
получить
однозначно
искомую
величину
.
Поль
-
зуясь
же
существующим
стандартом
это
сделать
невозможно
.
Определим
в
качестве
примера
коэффициент
структурного
ослабления
для
следующих
данных
,
полученных
в
результате
лабораторных
испытаний
образ
-
цов
:
средняя
прочность
образцов
R
=
40
МПа
;
коэффициент
вариации
прочности
Рис
. 6.2.
Зависимость
коэффициента
структурного
ослабления
от
относитель
-
ной
вариации
прочности
и
уровня
надежно
-
сти
(
вероятности
р
): I –
логарифмически
нормальный
закон
распределения
; II –
нор
-
мальный
закон
распределения
; 1 – p=0,99;
2 – p=0,95; 3 – p =0,9
соответственно
В
ЕРОЯТНОСТНО
-
СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЧНОСТИ ПОРОДНОГО МАССИВА С УЧЕТОМ МАКРОДЕФЕКТОВ
153
образцов
=0,35. Пусть по данным натурных наблюдений в массиве преобла-
дают кососекущие трещины с углом падения 40-45
0
, среднее расстояние между
которыми
m
=0,1 м. Такая густота трещин характерна для маломощных пород с
небольшой прочностью, например, для аргиллитов [148]. В соответствии со
СНиП [219], при расстояниях между трещинами 0,5…0,1 м величину
c
k
, со-
гласно таблице 5.4, следует принять равной 0,4. Получим теперь эту величину
на основе вероятностно-статистического подхода.
Рис. 6.3. Зависимость коэффициента структурного ослабления от расстояния
между трещинами и угла падения основной системы трещин при относитель-
ной вариации прочности образцов
=0,5 и при углах падения трещин:
1 –
=20
0
-45
0
; 2 –
=50
0
-65
0
; 3 –
=70
0
-75
0
; 4 –
=75
0
-80
0
; 5 –
=85
0
-90
0
;
6, 7 – рекомендации СНиП
Исходя из значения относительной вариации, можно было бы выдвинуть
гипотезу о нормальном распределении структурных элементов, и тогда по фор-
муле (5.8), задаваясь надежностью
р=
0,95, получим, что
c
k
= 0,59. Таким обра-
зом, без учета наличия трещин значение коэффициента структурного ослабле-
ния получается завышенным по сравнению со значением, рекомендуемым
СНиП.
Р
АЗДЕЛ
6
154
Учтем
теперь
наличие
макродефектов
по
методике
,
изложенной
выше
.
При
размере
стандартного
образца
0
l
=0,05
м
получим
,
что
0
l
m
= 2.
Для
кососекущих
трещин
функция
снижения
прочности
в
соответствии
с
(5.49)
равна
)
(
α
f
=0,3.
Тогда
относительная
вариация
/
η
для
«
исправленного
»
статистического
ряда
в
соответствии
с
(6.1)
или
графиком
6.1
будет
равна
0,8.
При
таком
значении
относительной
вариации
гипотеза
о
нормальном
распреде
-
лении
должна
быть
отвергнута
.
Значения
асимметрии
и
эксцесса
свидетельст
-
вуют
в
пользу
логарифмически
нормального
распределения
.
Тогда
по
формуле
(6.17)
получим
,
что
c
k
= 0,25.
Эта
величина
на
37%
меньше
величины
,
рекомен
-
дованной
СНиП
.
Соответственно
меньшим
будет
и
расчетное
значение
прочно
-
сти
массива
на
сжатие
.
При
расстоянии
между
трещинами
,
равном
0,5
м
,
в
соответствии
со
СНиП
величина
коэффициента
структурного
ослабления
будет
такой
же
как
и
в
пре
-
дыдущих
расчетах
,
т
.
е
c
k
=0,4.
На
основе
вероятностного
подхода
для
этого
случая
получим
:
0
l
m
=10;
η
′
=0,55;
c
k
=0,38.
Таким
образом
,
в
соответствии
с
СНиП
уменьшение
расстояния
между
трещинами
от
0,5
м
до
0,1
м
не
оказывает
влияние
на
величину
прочности
породного
массива
.
В
соответствии
с
расчетом
по
предложенной
методике
эта
величина
уменьшается
на
35%.