ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 1736
Скачиваний: 2
З
АКОНОМЕРНОСТИ
РАЗРУШЕНИЯ
ГОРНЫХ
ПОРОД
ЗА
ПРЕДЕЛОМ
ПРОЧНОСТИ
35
Рис
. 2.4.
Графики
деформирования
пильных
известняков
Крыма
(
известняк
М
)
Рис
. 2.5.
Графики
деформирования
каменной
соли
Р
АЗДЕЛ
2
36
Рис
. 2.6.
Графики
деформирования
осадочных
пород
Никополь
-
Марганецкого
месторождения
[117]
(
глина
зеленая
)
Рис
. 2.7.
Этапы
деформации
горных
пород
за
перелом
прочности
З
АКОНОМЕРНОСТИ
РАЗРУШЕНИЯ
ГОРНЫХ
ПОРОД
ЗА
ПРЕДЕЛОМ
ПРОЧНОСТИ
37
В
области
V
коэффициент
Пуассона
равен
0,5,
деформирование
материала
происходит
без
увеличения
объема
(
0
3
2
1
=
+
+
=
ε
ε
ε
ε
v
).
Эта
область
очень
ма
-
ла
для
хрупких
материалов
,
к
которым
относится
большинство
горных
пород
,
и
достаточно
велика
для
пластичных
материалов
с
выраженными
вязкими
свой
-
ствами
,
например
,
металлов
,
каменной
соли
или
марганецких
глин
(
см
.
рис
. 2.5
и
2.6).
В
области
VI
происходит
постепенное
разрушение
структурных
связей
,
поворот
и
сдвиг
отдельных
кристаллов
.
Коэффициент
Пуассона
здесь
больше
0,5,
деформирование
материала
сопровождается
увеличением
объема
(
0
3
2
1
>
+
+
=
ε
ε
ε
ε
v
).
Прочность
образцов
падает
,
однако
на
любом
уровне
на
-
гружения
оставшиеся
структурные
связи
обеспечивают
их
прочность
и
способ
-
ность
к
упругому
деформированию
,
о
чем
свидетельствуют
петли
гистерезиса
,
получаемые
при
циклическом
нагружении
и
разгрузке
(
см
.
рис
. 2.2-2.4).
При
-
близительная
параллельность
петель
гистерезиса
позволяет
и
в
запредельной
области
использовать
ту
же
величину
модуля
Юнга
,
что
и
в
упругой
.
Следует
отметить
также
,
что
при
деформировании
пластичных
пород
петли
гистерезиса
имеют
меньшую
площадь
,
т
.
е
.
диссипация
упругой
энергии
для
них
ниже
,
чем
для
хрупких
пород
.
Крутизна
ниспадающей
ветви
графиков
«
ε
σ
−
»
отражает
структурные
особенности
горных
пород
,
их
склонность
к
хрупкому
разрушению
.
Часто
эту
часть
диаграммы
линеаризируют
и
тогда
крутизна
ее
может
быть
оценена
чис
-
ленно
с
помощью
так
называемого
модуля
спада
,
или
хрупкости
.
Величина
эта
определяется
как
отношение
ε
σ
d
d
M
=
в
наиболее
крутой
части
ниспадающей
ветви
графика
ε
σ
−
.
Если
М
=0,
то
испытуемый
материал
будет
идеально
пла
-
стичен
,
а
если
∞
→
M
,
то
–
идеально
хрупок
.
Ваверсик
,
Файрхурст
и
Браун
ут
-
верждают
[114, 115],
что
существуют
горные
породы
,
способные
накапливать
в
себе
потенциальной
энергии
больше
,
чем
этого
требуется
для
их
разрушения
(
рис
. 2.8),
что
с
физической
точки
зрения
объяснить
очень
непросто
.
По
этому
признаку
авторы
работ
[114, 115]
выделяют
два
соответствующих
типа
горных
Р
АЗДЕЛ
2
38
пород
:
обычные
,
для
разрушения
ко
-
торых
требуется
ровно
столько
энер
-
гии
,
сколько
способны
выдержать
структурные
связи
(
0
p
M
),
и
склон
-
ные
к
бурному
разрушению
,
для
раз
-
рушения
которых
требует
больше
энергии
,
чем
способны
выдержать
структурные
связи
(
0
f
M
).
Область
VII (
см
.
рис
. 2.7)
харак
-
теризуется
полной
дезинтеграцией
испытуемых
образцов
,
некоторая
це
-
лостность
которых
обеспечивается
благодаря
внутреннему
трению
и
за
-
цеплению
соприкасающихся
частей
.
Дальнейшего
увеличения
объема
не
происходит
.
На
этом
уровне
нагружения
говорят
о
так
называемой
остаточной
прочности
ост
R
горных
пород
и
о
макси
-
мальном
значении
величины
объемного
разрыхления
*
v
ε
.
Для
учета
эффекта
ос
-
таточной
прочности
при
решении
задач
механики
горных
пород
удобно
поль
-
зоваться
коэффициентом
остаточной
прочности
c
ост
ост
R
R
k
=
,
где
c
R
–
предел
прочности
на
одноосное
сжатие
.
Эта
величина
отражает
структурные
особен
-
ности
деформируемого
материала
,
число
,
характер
и
вид
поверхностей
разру
-
шения
.
В
совокупности
с
модулем
Юнга
,
коэффициентом
Пуассона
,
коэффициен
-
том
дилатансии
(1+
*
v
ε
)
и
пределом
прочности
на
одноосное
сжатие
коэффици
-
ент
остаточной
прочности
дополняет
информацию
об
исследуемой
литологиче
-
ской
разности
с
точки
зрения
ее
прочности
,
структуры
и
поведения
в
обнаже
-
ниях
.
Рис
. 2.8.
Характерные
графики
за
-
предельного
деформирования
горных
пород
разной
степени
хрупкости
[114, 115]
З
АКОНОМЕРНОСТИ
РАЗРУШЕНИЯ
ГОРНЫХ
ПОРОД
ЗА
ПРЕДЕЛОМ
ПРОЧНОСТИ
39
Имеется
также
ряд
работ
[4, 115, 116],
в
кото
-
рых
исследуется
поведе
-
ние
горных
пород
в
объ
-
емном
напряженном
со
-
стоянии
при
«
жестком
»
их
нагружении
.
Типичные
графики
«
ε
σ
−
»,
полу
-
ченные
в
результате
таких
испытаний
,
показаны
на
рис
. 2.9.
Они
свидетельст
-
вуют
о
том
,
что
в
условиях
объемного
сжатия
хрупкость
горных
пород
снижается
.
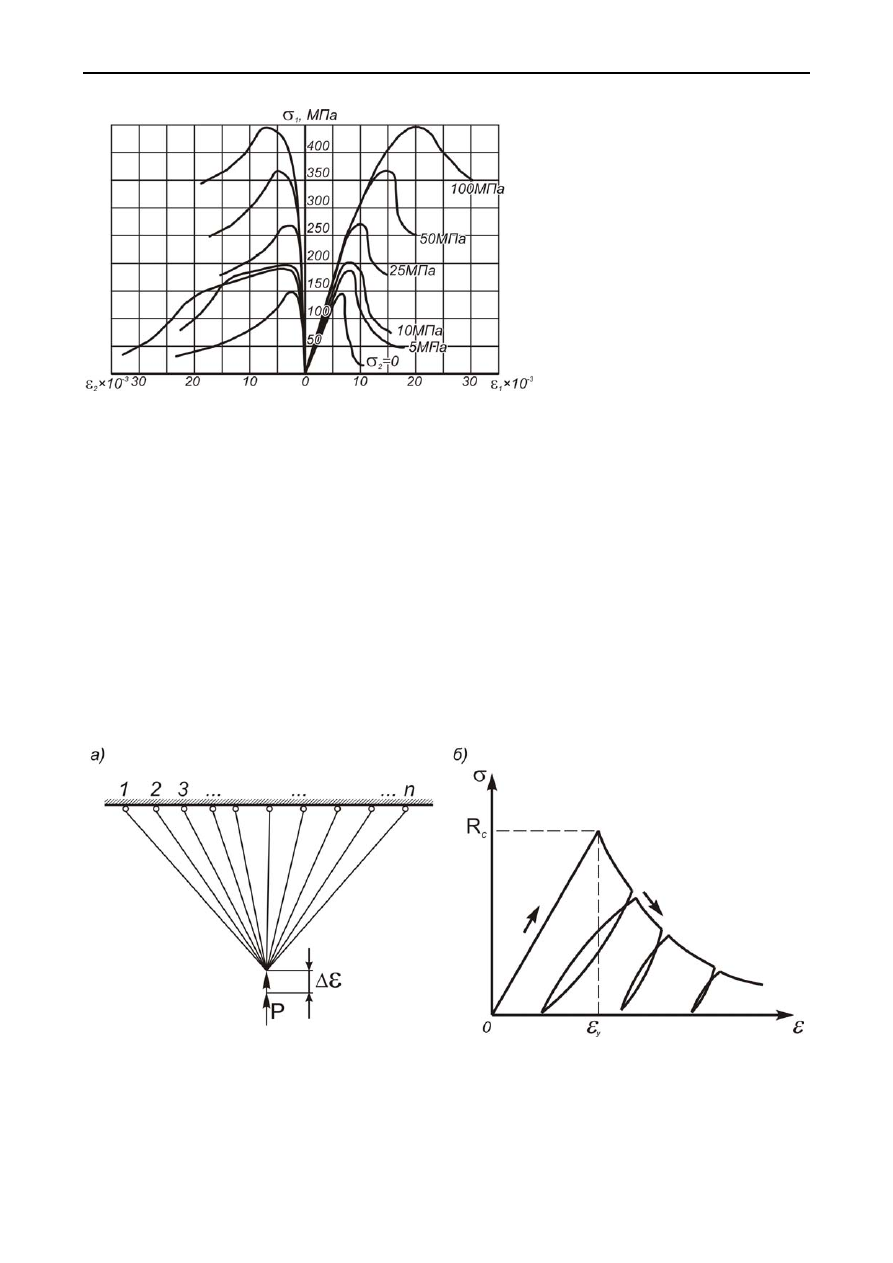
Описанный
выше
процесс
деформирования
горных
пород
за
пределом
прочности
наглядно
может
быть
представлен
в
виде
механической
модели
,
изо
-
браженной
на
рис
. 2.10,
а
.
Рис
. 2.10.
Структурная
механическая
модель
деформирования
горных
пород
за
пределом
прочности
:
а
)
структурная
модель
;
б
)
модельный
график
деформи
-
рования
Рис
. 2.9.
Типичные
графики
запредельного
де
-
формирования
горных
пород
в
условиях
объем
-
ного
сжатия
[4]