ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.04.2021
Просмотров: 341
Скачиваний: 1
16
Блок
.
Бл ок
–
это
гибкая
свя зь
,
у
которой
второй
конец
п ереброшен
ч ерез
диск
и
на
конц е
п рил ож ена
сил а
(
груз
), (
рис
.5.7.
а
).
Бл ок
меня ет
нап равл ение
сил ы
,
но
не
меня ет
ее
велич ины
.
П рименя я
п ринц ип
освобож даемости
от
свя зи
в
этом
сл уч ае
,
отбрасы ваем
груз
вместе
с
диском
.
Точ ка
п рил ож ения
реакц ии
находится
на
теле
.
Реакц ия
нап равл ена
такж е
,
как
в
сл уч ае
гибкой
свя зи
(
рис
.5.7.
б
).
С ферич еск ий
шарнир
.
Э тот
вид
свя зи
встречается
тол ько
в
п ространственны х
задач ах
.
С ф ерич еский
шарнир
п редставл я ет
собой
две
вл ож енны е
друг
в
друга
сф еры
.
В нешня я
сф ера
ж естко
закрепл ена
,
а
внутрення я
свободно
вращ ается
.
Как
и
в
сл уч ае
ц ил индрич еского
шарнира
,
реакц ия
п роходит
ч ерез
ц ентр
шарнира
,
и
точ ку
соп рикосновения
сф ер
.
Е е
нап равл ение
и
велич ина
обусл овл ены
внешней
нагрузкой
.
Д л я
удобства
реакц ию
раскл ады ваю т
на
три
взаимно
п ерп ендикул я рны е
составл я ю щ ие
(
рис
.
5.8.
а
,
б
).
П одпят ник
.
Как
и
сф ерич еский
шарнир
,
п одп я тник
встречается
,
в
основном
,
в
п ространственны х
задач ах
.
О н
п редставл я ет
собой
ц ил индрич еский
шарнир
с
уп ором
на
одном
конц е
,
п оэтому
к
двум
составл я ю щ им
реакц ии
17
ц ил индрич еского
шарнира
добавл я ется
реакц ия
от
уп ора
,
которая
нап равл ена
всегда
в
сторону
п ротивоп ол ож ную
уп ору
(
рис
. 5.9.
а
,
б
).
В
точ ке
А
п одп я тник
,
а
в
точ ке
В
ц ил индрич еский
шарнир
.
Е сл и
п одп я тник
встречается
в
п л оской
задач е
,
то
одна
из
составл я ю щ их
реакц ии
,
А
Х
,
будет
отсутствовать
.
Заделк а
.
Рассмотрим
заделку
в
сл уч ае
п л оской
задач и
.
П римером
мож ет
сл уж ить
п л ита
,
вц ементированная
в
стену
,
гвоздь
вбиты й
в
стену
и
т
.
д
.
Э тот
вид
свя зи
не
п озвол я ет
телу
не
тол ько
сдвинуться
в
какую
-
л ибо
сторону
,
но
и
п овернуться
на
какой
-
л ибо
угол
.
С л едовательно
,
к
двум
составл я ю щ им
реакц ии
заделки
нуж но
добавить
момент
заделки
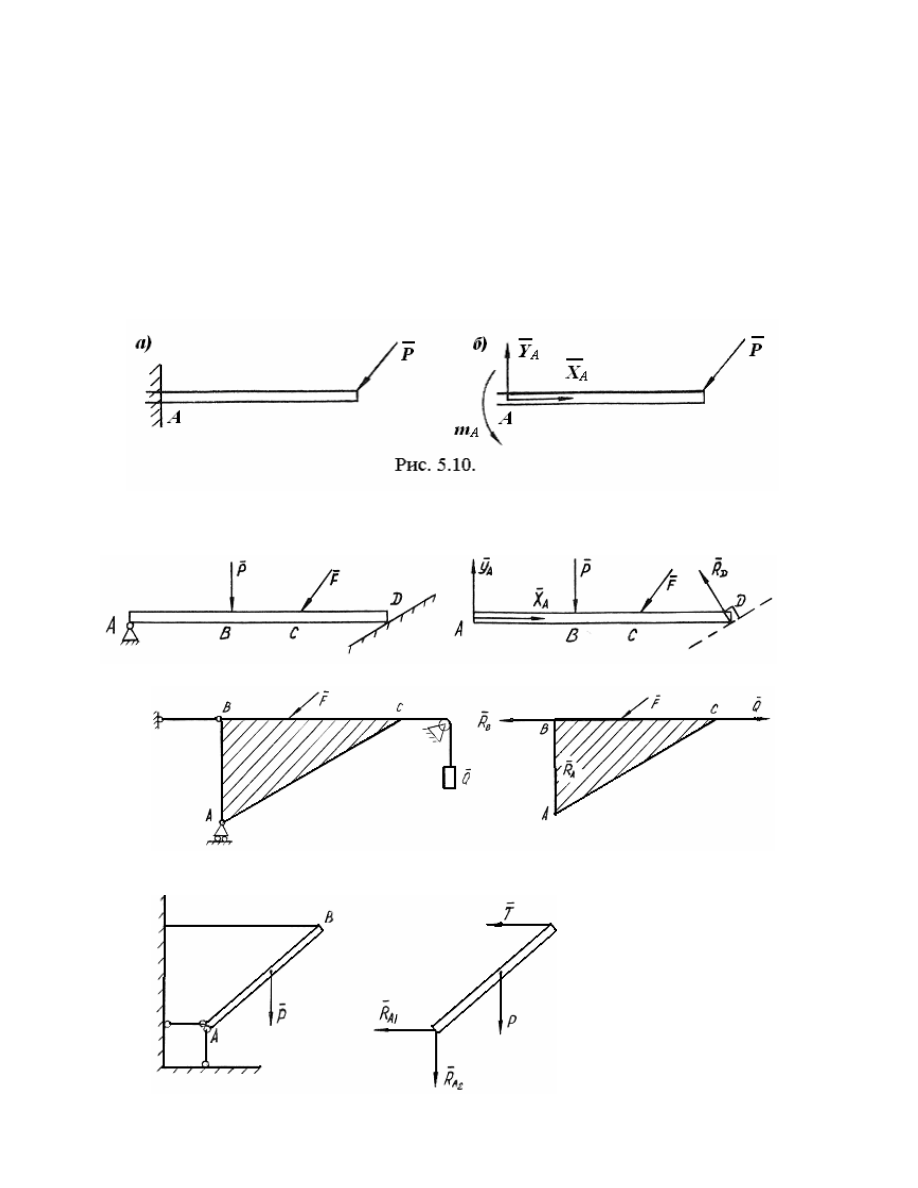
A
m
(
рис
. 5.10.).
П рим е ры
ос вобожд е н ия
те л
от
с вязе й
.
П ример
1.
П ример
2.
П ример
3.
18
§
6.
Ус ловия
равн ове с ия
с ис те м ы
с ил
.
П усть
дана
система
сил
)
F
F
F
(
S
n
Κ
2
1
.
Глав ным
в ек т ором
системы
сил
назы вается
п остроенны й
в
п ол ю се
А
свободны й
вектор
∑
=
=
n
i
i
A
F
R
1
(
рис
. 6.1.)
Глав ным
м ом ент ом
системы
сил
относительно
п ол ю са
А
назы вается
векторная
сумма
моментов
сил
,
вы ч исл енны х
относительно
п ол ю са
А
(
рис
.
6.2.).
Т еорем а
(
необходимое
и
достаточ ное
усл овие
равновесия
системы
сил
).
Д л я
того
ч тобы
система
сил
находил ась
в
равновесии
необходимо
и
достаточ но
,
ч тобы
ее
гл авны й
вектор
и
гл авны й
момент
относительно
п роизвол ьного
ц ентра
бы л и
равны
нул ю
,
то
есть
:
0
=
A
R
, (6.1)
0
=
A
m
. (6.2)
1
F
2
F
3
F
1
F
2
F
n
F
A
R
Рис
. 6.1.
А
A
R
А
1
F
2
F
n
F
1
r
2
r
n
r
( )
1
A
F
m
( )
2
A
F
m
( )
n
A
F
m
[
]
∑
=
=
n
1
i
i
i
A
F
,
r
M
Рис
. 6.2.
19
У равнения
(6.1)
и
(6.2)
п редставл я ю т
собой
два
векторны х
уравнения
.
Е сл и
расп исать
их
в
п роекц ия х
на
оси
то
п ол уч им
шесть
ал гебраич нских
уравнений
,
которы е
назы ваю т
уравнения ми
равновесия
дл я
п ространственной
системы
сил
:
∑
=
=
n
i
ix
F
1
0 , (6.3)
∑
=
=
n
i
i
x
)
F
(
m
1
0 , (6.6)
∑
=
=
n
i
iy
F
1
0 , (6.4)
∑
=
=
n
i
i
y
)
F
(
m
1
0 , (6.7)
∑
=
=
n
i
iz
F
1
0 , (6.5)
∑
=
=
n
i
i
z
)
F
(
m
1
0 . (6.8)
Т еорем а
.
Д л я
равновесия
п роизвол ьной
п ространственной
системы
сил
необходимо
и
достаточ но
,
ч тобы
суммы
п роекц ий
всех
сил
на
каж дую
из
трех
координатны х
осей
и
суммы
их
моментов
относительно
этих
осей
бы л и
равны
нул ю
.
В
сл уч ае
п л оской
системы
сил
векторны е
уравнения
(6.1)
и
(6.2)
эквивал ентны
одной
из
ниж е
сл едую щ их
систем
.
П ри
этом
уравнение
(6.2)
дает
ал гебраич еское
уравнение
моментов
относительно
точ ки
.
1)
( )
(
)
( )
( )
11
6
0
10
6
0
9
6
0
1
0
1
1
.
.
F
m
.
,
F
.
,
F
n
i
i
n
i
iy
n
i
ix
=
=
=
∑
∑
∑
=
=
=
Д л я
равновесия
п роизвол ьной
п л оской
системы
сил
необходимо
и
достаточ но
,
ч тобы
суммы
п роекц ий
всех
сил
на
каж дую
из
двух
координатны х
осей
и
сумма
их
моментов
относительно
п роизвол ьного
ц ентра
,
л еж ащ его
в
п л оскости
действия
сил
,
бы л и
равны
нул ю
.
2)
( )
(
)
( )
(
)
(
)
14
6
0
13
6
0
12
6
0
1
1
1
.
.
F
.
,
F
m
.
,
F
m
n
i
ix
n
i
i
B
n
i
i
A
=
=
=
∑
∑
∑
=
=
=
Д л я
равновесия
п роизвол ьной
п л оской
системы
сил
необходимо
и
достаточ но
,
ч тобы
суммы
моментов
всех
сил
этих
относительно
каких
-
R
А
В
А
О
Х
20
нибудь
двух
ц ентров
А
и
В
и
сумма
их
п роекц ий
на
ось
О Х
,
не
п ерп ендикул я рную
п ря мой
АВ
,
бы л и
равны
нул ю
.
3)
( )
(
)
( )
(
)
( )
(
)
17
6
0
16
6
0
15
6
0
1
1
1
.
,
F
m
.
,
F
m
.
,
F
m
n
i
i
C
n
i
i
B
n
i
i
A
=
=
=
∑
∑
∑
=
=
=
Д л я
равновесия
п роизвол ьной
п л оской
системы
сил
необходимо
и
достаточ но
,
ч тобы
суммы
моментов
всех
этих
сил
относительно
л ю бого
из
трех
ц ентров
А
,
В
и
С
,
не
л еж ащ их
на
одной
п ря мой
,
бы л и
равны
нул ю
.
В
сл уч ае
системы
тел
решение
задач
статики
усл ож ня ется
.
В
ч исл о
неизвестны х
п омимо
реакц ий
свя зей
войдут
усил ия
ил и
моменты
,
возникаю щ ие
меж ду
телами
системы
.
Э то
требует
п ривл ечения
доп ол нительны х
уравнений
.
П риходится
разбивать
систему
на
ч асти
и
рассматривать
равновесие
каж дого
тела
,
п ривл екая
ф ормул ы
(6.3)
–
(6.9)
в
п ространственном
сл уч ае
и
ф ормул ы
(6.9)
–
(6.11) [(6.12)
–
(6.14), (6.15)
–
(6.17)]
в
п л оском
сл уч ае
.
§
7.
П рим е ры
.
П ри
решении
задач
статики
обы ч но
п ридерж иваю тся
сл едую щ его
ал горитма
:
1)
оп ределя ю т
тело
(
систему
тел
) ,
равновесие
которого
(
которой
)
надо
рассмотреть
,
ч тобы
оп ределить
искомы е
велич ины
.
В водя т
систему
координат
;
2)
есл и
среди
заданны х
активны х
сил
есть
расп ределенны е
сил ы
,
то
их
заменя ю т
равнодействую щ ей
(
см
.
§
4);
3)
оп ределя ю т
свя зи
и
их
тип ы
(
см
.
§
5);
4)
мы сл енно
отбрасы ваю т
свя зи
,
нал ож енны е
на
тело
(
систему
тел
)
и
заменя ю т
свя зи
реакц ия ми
свя зей
.
П ри
этом
точ ка
п рил ож ения
реакц ии
находится
на
рассматриваемом
теле
;
5)
рассматриваю т
равновесие
несвободного
тела
(
системы
тел
)
как
тела
свободного
п од
действием
активны х
сил
и
реакц ий
свя зей
,
то
есть
п рименя ю т
уравнения
равновесия
(6.3)
–
(6.8)
дл я
п ространственной
системы
сил
ил и
(6.9)
–
(6.11) [(6.12)
–
(6.14), (6.15)
–
(6.17)]
дл я
п л оской
системы
сил
;
6)
решаю т
уравнения
и
находя т
искомы е
велич ины
.
Как
п равил о
,
ими
я вл я ю тся
реакц ии
свя зей
.