Добавлен: 26.10.2023
Просмотров: 322
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
, отражающая знания экспертов о методах управления объектом в различных ситуациях, характере его функционирования в различных условиях и т.п., т.е. содержащая формализованные человеческие знания.
Простейший вариант правила нечеткой продукции, который наиболее часто используется в системах нечеткого вывода, может быть записан в форме:
«если "β1 есть α’", тогда "β2 есть α’’» (13) где нечеткое высказывание «β1 есть α’» представляет собой условие данного правила нечеткой продукции, а нечеткое высказывание «β2 есть α’’» - нечеткое заключение данного правила. При этом считается, что β1≠β2.
60
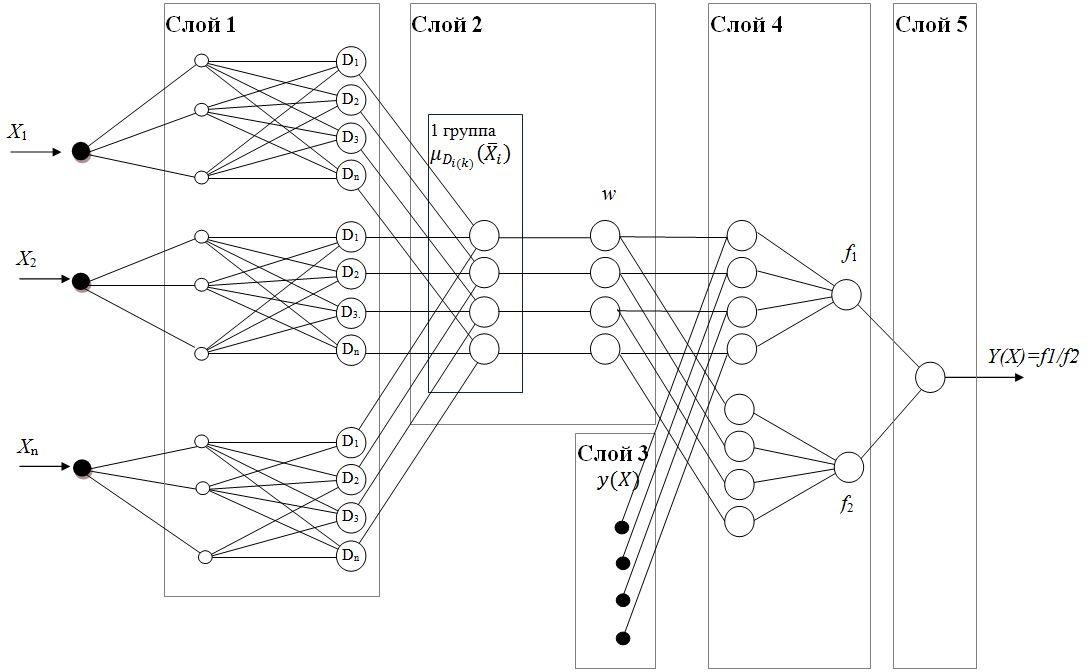
Рисунок 9 – Обобщенная структура нейро-нечеткого логического вывода
Для каждого параметра, описывающего состояние анализируемого объекта, важно определить количество функции принадлежности (диапазонов значений), наилучшим образом характеризующее данный параметр. Для этого необходимо исходить из рассматриваемой задачи и требуемой точности описания в рассматриваемой задаче.
Для каждого параметра, описывающего состояние анализируемого объекта, также важно определить вид функции принадлежности, наилучшим образом характеризующий данный параметр.
Рассмотрим так называемые стандартные функции принадлежности. Стандартные функции принадлежности легко
применимы к решению большинства задач.
Выделяют следующие типовые функции принадлежности 69:
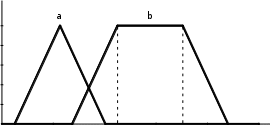
Примерами кусочно-линейных функций принадлежности (Рис. 10) являются треугольная (a) и трапециевидная (b).
õ
Рисунок 10 – кусочно-линейные функции принадлежности
В общем виде треугольные функции принадлежности аналитически можно представить следующим образом:
0, x a
x a

x b a
c x
, a x b
(13)
, b x c
c b
0, c x
где
a,b,c– произвольные значения, при условии, что a b c.
В общем виде трапециевидные функции принадлежности аналитически
можно представить следующим образом:
0, x a
x a

b a
1,
x
d x

d c
, a x bb x c
, c x d
(14)
0,
d x
где
a,b,c, d– произвольные значения, при условии, что a b c d.
Z-образная (с) и S-образная (d) функции принадлежности (Рис. 11)
представляют собой сплайн-функции.

õ
Рисунок 11 – Z-образная и S-образная функции принадлежности
В общем виде Z-образную функцию принадлежности аналитически можно представить следующим образом:
1 1
xa
x a
(х)
,a x b
(15)
0,
b a
x b
где
a,b– произвольные значения, при условии, что a b.
S-образную функцию принадлежности в аналитическом виде можно
представить следующим образом:
xb
cos ,a x b
(16)
1,
b a
x b
где
a,b– произвольные значения, при условии, что a b.
Частными случаями Z-образной и S-образной функций
принадлежности являются их линейные функции. Линейная S-образная функция в аналитическом виде представляется как
0, x a
(х) xa, a x b
b a
(17)
1, b x
где
как
a,b– произвольные значения, при условии, что a b.
Линейная Z-образная функция в аналитическом виде представляется
1, x a
(х) bx,a x b
b a
(18)
0, b x
где
a,b– произвольные значения, при условии, что a b.
Треугольные и трапециевидные функции принадлежности могут быть построены с помощью линейных Z-образной и S-образной функций принадлежности.
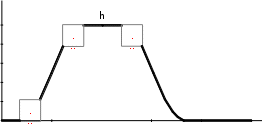
К отдельной группе можно отнести П-образные функции принадлежности: колоколообразную (Рис. 12) и гауссовы (Рис. 13) функции принадлежности.
õ
Рисунок 12 – Колоколообразная функция принадлежности
В общем виде колоколообразную функцию принадлежности можно представить следующим образом:

2b
 (х) 1
(х) 1
1
(18)
где
a,b,c– произвольные значения, при условии, что a b c
и b 0
75.
Также П-образные функции принадлежности могут быть построены с помощью Z-образной и S-образной функций принадлежности.
Гауссовы функции принадлежности бывают двух видов – симметричная гауссова (e) и двухсторонняя гауссова (f). Они формируются с использованием гауссова распределения.
Аналитически симметричную гауссову функцию принадлежности можно представить следующим образом:
Простейший вариант правила нечеткой продукции, который наиболее часто используется в системах нечеткого вывода, может быть записан в форме:
«если "β1 есть α’", тогда "β2 есть α’’» (13) где нечеткое высказывание «β1 есть α’» представляет собой условие данного правила нечеткой продукции, а нечеткое высказывание «β2 есть α’’» - нечеткое заключение данного правила. При этом считается, что β1≠β2.
60

Рисунок 9 – Обобщенная структура нейро-нечеткого логического вывода
-
Определениечислафункцийпринадлежности
Для каждого параметра, описывающего состояние анализируемого объекта, важно определить количество функции принадлежности (диапазонов значений), наилучшим образом характеризующее данный параметр. Для этого необходимо исходить из рассматриваемой задачи и требуемой точности описания в рассматриваемой задаче.
-
Определениевидафункций принадлежности
Для каждого параметра, описывающего состояние анализируемого объекта, также важно определить вид функции принадлежности, наилучшим образом характеризующий данный параметр.
Рассмотрим так называемые стандартные функции принадлежности. Стандартные функции принадлежности легко
применимы к решению большинства задач.
Выделяют следующие типовые функции принадлежности 69:
-
кусочно-линейные - набор отрезков прямых линий, образующих непрерывную или кусочно-непрерывную функцию; -
гауссовы – образованные на основе гауссова распределения; -
сигмоидную кривую и т. д.
Примерами кусочно-линейных функций принадлежности (Рис. 10) являются треугольная (a) и трапециевидная (b).

õ
Рисунок 10 – кусочно-линейные функции принадлежности
В общем виде треугольные функции принадлежности аналитически можно представить следующим образом:
0, x a
x a

x b a
c x
, a x b
(13)
, b x c
c b
0, c x
где
a,b,c– произвольные значения, при условии, что a b c.
В общем виде трапециевидные функции принадлежности аналитически
можно представить следующим образом:
0, x a
x a

b a
1,
x
d x

d c
, a x bb x c
, c x d
(14)
0,
d x
где
a,b,c, d– произвольные значения, при условии, что a b c d.
Z-образная (с) и S-образная (d) функции принадлежности (Рис. 11)
представляют собой сплайн-функции.

õ
Рисунок 11 – Z-образная и S-образная функции принадлежности
В общем виде Z-образную функцию принадлежности аналитически можно представить следующим образом:
1,
1 1
xa
x a
(х)
cos
,a x b
(15)
2 2
0,
b a
x b
где
a,b– произвольные значения, при условии, что a b.
S-образную функцию принадлежности в аналитическом виде можно
представить следующим образом:
0,
-
a
1 1
xb
(х)
cos ,a x b
(16)
2 2
1,
b a
x b
где
a,b– произвольные значения, при условии, что a b.
Частными случаями Z-образной и S-образной функций
принадлежности являются их линейные функции. Линейная S-образная функция в аналитическом виде представляется как
0, x a
(х) xa, a x b
b a
(17)
1, b x
где
как
a,b– произвольные значения, при условии, что a b.
Линейная Z-образная функция в аналитическом виде представляется
1, x a
(х) bx,a x b
b a
(18)
0, b x
где
a,b– произвольные значения, при условии, что a b.
Треугольные и трапециевидные функции принадлежности могут быть построены с помощью линейных Z-образной и S-образной функций принадлежности.
К отдельной группе можно отнести П-образные функции принадлежности: колоколообразную (Рис. 12) и гауссовы (Рис. 13) функции принадлежности.

õ
Рисунок 12 – Колоколообразная функция принадлежности
В общем виде колоколообразную функцию принадлежности можно представить следующим образом:

2b
 (х) 1
(х) 1 1
(18)
где
a,b,c– произвольные значения, при условии, что a b c
и b 0
75.
Также П-образные функции принадлежности могут быть построены с помощью Z-образной и S-образной функций принадлежности.
Гауссовы функции принадлежности бывают двух видов – симметричная гауссова (e) и двухсторонняя гауссова (f). Они формируются с использованием гауссова распределения.
Аналитически симметричную гауссову функцию принадлежности можно представить следующим образом: