Добавлен: 26.10.2023
Просмотров: 310
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
(х) e
xb2
2c2
(17)
Двухстороннюю гауссову функцию принадлежности аналитически
можно представить как
1 ... 6 7 8 9 10 11 12 13 ... 18
exp
х с2 / 2a2 2
, x c1
1 1
(х)
c x c
(18)
1,
1 2
exp х с2
2 / 2a2 2
, x c2
где
a1,a2 ,c1,c2
-
произвольные значения, при условии, что c1 c2 .

õ
Рисунок 13 – Гауссовы функции принадлежности
С помощью двухсторонней гауссовой функции принадлежности можно использовать ассиметричные функции принадлежности.
Если
c1 c2 , то гауссову функцию принадлежности аналитически
можно представить следующим образом:
1 1
exp х с2 / 2a2 2 , x c
2
1 1 2 2 2 1
(х) exp х с2 / 2a2 2 exp х с2 / 2a2 2 , c x c
(19)
exp
х с
2 / 2a2 2
, x c
2 2 1
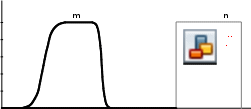
Сигмоидные функции (Рис. 14) строятся с использованием сигмоидной кривой. В общем виде сигмоидную функцию принадлежности (n) можно представить следующим образом:
1 ... 7 8 9 10 11 12 13 14 ... 18
(х)
1
 1 ea( xc)
1 ea( xc)(20)
Произведение двух сигмоидных функций (m) принадлежности выглядит следующим образом:
(х)
1
 1 ea1 ( xc1 )
1 ea1 ( xc1 ) 1
 1 ea2 ( xc2 )
1 ea2 ( xc2 )(21)
 õ
õРисунок 14 – Сигмоидные функции принадлежности
Однако если предстоит решать специфическую задачу, можно выбрать и более подходящую форму функции принадлежности, при этом можно добиться лучших результатов работы системы, чем при использовании функций стандартного вида 74.
Все методы построения функций принадлежности условно можно разделить на два вида: прямые и косвенные. Прямые методы реализуются на основе экспертного задания вида функций принадлежности. К прямым методам можно отнести метод статистической обработки экспертной информации [80]. Существенными недостатком такого метода является его ориентация на преимущественно субъективную информацию о процессе и/или явлении и обязательном принятии допущений при преобразовании данной информации в степени принадлежности нечетких множеств.
Косвенные методы предполагают выбор функций принадлежности, заранее удовлетворяющих сформулированным условиям. Следует отметить, что экспертная информация имеет статус первичной, что предполагает дальнейшую обработку, в том числе с учетом дополнительных условий. Дополнительные условия могут накладываться как на вид получаемой
информации, так и на процедуры ее обработки. Наиболее распространенным среди косвенных является метод парных сравнений, в результате применения которого формируется матрица парных сравнений [81]. Основным недостатком данного метода является сложность выполнения сравнений в случае оценивания большого числа вариантов.
Помимо метода парных сравнений в ряде случаев представляет интерес метод идентификации функций принадлежности на базе определения по экспериментальным данным нечетких моделей типа «входы - выход». Такой метод позволяет решить задачу формализации исходной информации, хотя предъявляет повышенные требования к обучающей выборке и модели типа
«вход-выход» [82,83].
В отдельную группу можно выделить методы определения функций принадлежности с помощью кластеризации. В общем случае под кластеризацией подразумевается объединение объектов в группы (кластеры) на основе однотипности каких-либо признаков для объектов одной группы и отличий данных признаков между группами. Большинство существующих алгоритмов кластеризации не требует принятия допущений, свойственных, например, статистическим методам.
Задача кластеризации состоит в определении естественного разбиения данных на классы независимо от субъективного суждения эксперта. Важнейшей особенностью методов кластеризации является их использование в условиях отсутствия какой-либо информации о законах распределения данных [83]. Следует отметить, что кластеризация может быть выполнена для объектов как с качественными, так и количественными или даже смешанными признаками.
Методы кластеризации делятся на четкие и нечеткие. Задача четких методов кластеризации заключается в разбиении