Добавлен: 26.10.2023
Просмотров: 325
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
проявления фактора ki
на любом объекте;
P(Di
ki)
-
апостериорная
вероятность состояния Di
при проявлении фактора
ki.
Основная идея метода Байеса заключается в оценке вероятностной
характеристики выявления состояния
P(Di
ki)
на основе доступных для
анализа факторов. При последовательном рассмотрении различныхкомбинаций факторов увеличение значения
P(Di
ki)
свидетельствует о
высокой вероятности события нереализуемости.Di, а снижение – о его практической
Для определения состояний силового масляного трансформатора
110 кВ введем классификацию состояний электрооборудования (Табл. 2), содержащую четыре позиции, в зависимости от состояния показателя (его соответствия или не соответствия нормальному состоянию) и наличия дефекта.
Таблица 2 – Возможные состояния оборудования
| Состояние | Показатель в пределах нормы | Наличие дефекта |
| D1 | Да | Нет |
| D2 | Да | Да |
| D3 | Нет | Да |
| D4 | Нет | Нет |
Далее определяются априорные вероятности исходных состояний
с помощью экспертных оценок.
Будем считать, что признаки являются независимыми. В этом случае состояние силового трансформатора описывается комплексом независимых признаков K, каждый из которых является двухразрядным:
K (k1, k2 ),
(2)
где k1
-
проявление признака K, а
k2 – непроявление.
Вероятности проявления и/или непроявления могут быть представлены функциями распределения (Рис. 3). На рисунке представлены функции
проявления признаков состояний:
D1 –
1 (x) , D2
– 2 (x) ,
D3 –
3 (x) , и D4 –
4 (x) , которые могут быть определены на интервале
X0...3.
Значение независимой переменной характеризует ранг состояния объекта исследования.
0 0,5 1 1,5 2 2,5 3
Рисунок 3 – Функции распределения проявления признаков состояний
Обобщенные линеаризованные представления функций сильного
1 (x)
и нормального
2 (x)
проявления признаков дают вероятностные
характеристики проявления какого-либо признака
P( x)
одновременно с
тем, как обобщенные линеаризованные представления функций слабого
проявления
3 (x)
и его отсутствия
4 (x)
дают вероятностные
характеристики непроявления признаков
N( x) .
Характеристические функции
P( x) и
N( x)
позволяют определить
распределение вероятностей проявления признаков для определенного
диагноза Di
(Рис. 4).
Аналогичные функции должны быть определены для всех диагностируемых признаков для каждого состояния объекта исследования, описанного в Табл. 2.
Вероятность каждого возможного состояния при различных сочетаниях
признаков может быть определена по формуле Байеса:
P D
/ K
PDi PK/ Di ,
(3)
/ K
PDi PK/ Di ,
(3)
s1
s s
in
P D P K/ D
где K – множество двухразрядных признаков k1, k2, k3,..., kv, n – число
диагнозов состояния,
PDi – предварительная вероятность диагноза
Di,
PK/ Di
-
вероятность проявления признаков в диагнозе
Di, определяемая
в соответствии с выражением:
PK/ Di Pk1 / Di Pk2 / DiPkv/ Di,
где K– множество двухразрядных признаков k1, k2, k3,..., kv.
(4)
Такой анализ позволяет получить количественную характеристику сочетания диагностируемых признаков состояния по принадлежности тому или иному состоянию.
Для хроматографического анализа газов, растворенных в масле (ХАРГ) анализ выполняется для семи газов (Табл. 3): метан (CH4 ), углекислый газ ( CO2 ), этилен ( C2 H4 ), ацетилен ( C2 H2 ), этан ( C2 H6 ), водород ( H2 ), угарный
газ ( CO).
10,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
0 0,5 1 1,5 2 2,5 3
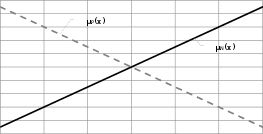
Рисунок 4 - Характеристические функции вероятностного проявления
признаков
С целью подтверждения проведенных исследований был выполнен расчет вероятностей состояний на основе данных ХАРГ силового трансформатора с использованием функций принадлежности, а также вероятностей проявлений и непроявлений признаков для каждого газа в отдельности. Расчет вероятностей состояний силового трансформатора для ряда сочетаний признаков приведен в Табл. 3.
Затем был выполнен расчет вероятности диагноза Di
при соответствии
всего комплекса признаков
K k11 k21 k31 k41 k51 k61 k71,
представленных в Табл. 3, нормальным граничным условиям, согласно выражению (3):
PD1 / K 0,5 0,998 0,990 0,940 0,895 0,821 0,804 0,990 /