Добавлен: 26.10.2023
Просмотров: 134
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Приложение 1
8 класс. Окружность. Взаимное расположение прямой и окружности.
Главная дидактическая цель урока: Добиться умения самостоятельно формулировать определения понятий: окружность, радиус, диаметр, хорда каждым учащимся.
Цели урока:
Изучить возможности взаимного расположения прямой и окружности.
Способствовать формированию приёмов критического мышления, анализа и синтеза
Воспитание коммуникативной культуры, приобретение опыта самостоятельной работы.
| ЭТАПЫ УРОКА | ЗАДАЧИ ЭТАПА | ИНСТРУКЦИЯ ПО ВЫПОЛНЕНИЮ | РЕЗУЛЬТАТ |
| 1. Орг. этап. | Подготовить уч-ся к работе на уроке. | Приветствие. Организация внимания. | |
| 2. Подготовка к изучению нового материала. | Организация познавательной деятельности уч-ся. | Сообщить тему урока. Игра “Верю-не верю ”. Какова, ребята, по вашему мнению, будет цель нашего урока? | В тетради число и тема урока. Сформулировать цель урока. |
| 3. Усвоение новых знаний. (сам – но) | Дать конкретное представление об изучаемых понятиях. Сформулировать их определение. Проанализировать связь между ними. | 1.Читайте текст лист №1 . 2.Что нового вы узнали? Сравнили с ответами “верю-не верю” в начале урока. 3.Составьте таблицу вопросов по тексту. 4. Обменяйтесь вопросами и ответами с соседом. 5.Работайте с таблицей лист №2. Используя опорные слова, сформулируйте определения, обсудите их с соседом по парте. 6.Практическая работа лист №3 Выполнить и сделать выводы. | В тетради таблица вопросов. В тетради записаны определения окружности, радиуса, хорды диаметра, Практическая работа в тетради. Вывод. |
| 4. Проверка понимания нового материала (Фронт.) | Осмысление новых понятий и закономерностей. Устранить обнаруженные пробелы. | Обсуждаем с классом выполненные задания, определения и выводы. Знакомимся с материалом в учебнике | В тетради устранены возникшие пробелы |
| 5. Закрепление (Самостоятельная работа) | Закрепить знания и умения по новому материалу. | 1.Задача: 2..Составьте свою задачу на взаимное расположение прямой и окружности. | Ответ с объяснением в тетради. |
| 6. Подведение итогов | Сообщить д\з. Подвести итоги. | Что нового узнали на уроке? Как вы понимаете эпиграф перед текстом на листе. Оцените свою работу: …- всё понял и могу рассказать. …-всё понял , но рассказать не могу. …-.понял не всё. | Воспроизвести изучаемые понятия. Выставить отметки уч-ся правильно отвечающим на уроке. |
Игра “Верю-не верю” (ОКРУЖНОСТЬ)
Цель игры: Вызвать интерес к изучению темы “окружность”, создать положительную мотивацию самостоятельного изучения текста по теме.
Проводится в начале урока, после сообщения темы.
| Вопрос | “+” верю, “-” неверю |
| 1. Верите ли вы, что самая простая из кривых линий – окружность? | |
| 2. Верите ли вы, что древние индийцы считали самым важным элементом окружности радиус, хотя не знали такого слова? | |
| 3. Верите ли вы, что впервые термин “радиус” встречается лишь в 16 веке? | |
| 4. Верите ли вы, что в переводе с латинского радиус означает “луч”? | |
| 5. Верите ли вы, что при заданном периметре именно окружность ограничивает наибольшую площадь? | |
| 6. Верите ли вы, что в русском языке слово “круглый” означает высшую степень чего-либо? | |
| 7. Верите ли вы, что выражение “ходить по кругу” когда-то означало “прогресс”? | |
| 8. Верите ли вы, что хорда в переводе с греческого означает “струна”? | |
| 9. Верите ли вы, что определение “касательной” уже есть в первом учебнике геометрии - “Начала” Евклида? | |
Далее предлагается текст.
ЛИСТ №1
“Ни 30 лет, ни 30 столетий не оказывают никакого влияния на ясность или на красоту геометрических истин”. Кэрролл Л.
Самая простая из кривых линий – окружность. Это одна из древнейших геометрических фигур. Ещё вавилоняне и древние индийцы считали самым важным элементом окружности – радиус. Слово это латинское и означает “луч”. В древности не было этого термина: Евклид и другие учёные говорили просто “прямая из центра”, Ф. Виет писал что “радиус” - это “элегантное слово”. Общепринятым термин “радиус” становится лишь в конце XVII в. Впервые термин “радиус” встречается в “Геометрии” французского ученого Рамса, изданной в 1569 году.
В Древней Греции круг и окружность считались венцом совершенства. Действительно в каждой своей точке окружность “устроена” одинаково, что позволяет ей как бы двигаться “по себе”. На плоскости этим свойством обладает еще лишь прямая. Одно из интереснейших свойств круга состоит в том, что он при заданном периметре ограничивает максимальную площадь.
В русском языке слово “круглый” тоже стало означать высокую степень чего-либо: “круглый отличник”, “круглый сирота” и даже “круглый дурак”.
Если вы когда-либо пробовали получить информацию от бюрократической организации, вас, скорее всего “погоняли по кругу”. Фраза “ходить по кругу” обычно не ассоциируется с прогрессом. Но в период индустриальной революции, выражение “ходить по кругу” очень точно отражало прогресс. Шкивы и механизмы давали машинам возможность увеличить производительность и значит сократить рабочую неделю.
Без понятия круга и окружности было бы трудно говорить о круговращении жизни. Круги повсюду вокруг нас. Окружности и циклы идут, взявшись за руки. Циклы получаются при движении по кругу. Мы изучаем циклы земли, они помогают нам разобраться, когда надо сажать растения и когда мы должны вставать.
Представление об окружности даёт линия движения модели самолёта, прикреплённого шнуром к руке человека, также обод колеса, спицы которого соответствуют радиусам окружности.
Термин “хорда” (от греческого “струна”) был введён в современном смысле европейскими учёными в XII-XIII веках.
Определение касательной как прямой, имеющей с окружностью только одну общую точку, встречается впервые в учебнике “Элементы геометрии” французского математика Лежандра (1752-1833 гг.). В “Началах” Евклида даётся следующее определение: прямая касается круга, если она встречает круг, но при продолжении не пересекает его
По материалам книг: Г. Глейзер “История математики в школе”, С Акимова “Занимательная математика”.
Прочитав текст, составьте в тетради таблицу вопросов по нему, так чтобы вопрос начинался с указанного слова.
| Что? | Кто? | Где? | Когда? | Почему? | Зачем? |
| | | | | | |
ЛИСТ №2
Изучив таблицу, сформулируйте геометрические определения понятий, используя ключевые слова.
| № | рисунок | Определяемое понятие | Используемые ключевые понятия |
| 1 |  | Окружность | Точки плоскости, одинаковое расстояние, точка - центр. |
| 2 | 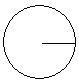 | радиус | Точки окружности, центр окружности, отрезок. |
| 3 | 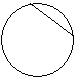 | Хорда | Отрезок, точки окружности. |
| 4 | 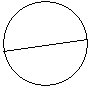 | Диаметр | Хорда окружности, центр окружности. |
ЛИСТ №3
ПРАКТИЧЕСКАЯ РАБОТА. Рассмотрите прямую m, точку М вне её и отрезок МК.
П
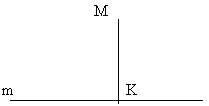остройте в тетради три окружности с центром в точке М: 1. Радиус окружности r < MK
2. Радиус окружности r = MK
3. Радиус окружности r >MK
Дайте определение расстояния от точки до прямой: Расстояние от точки до прямой – это
| Радиус окружности меньше расстояния от центра окружности до прямой | Радиус окружности больше расстояния от центра окружности до прямой | Радиус окружности равен расстоянию от центра окружности до прямой |
| Прямая и окружность ………. | Прямая и окружность ………. | Прямая и окружность ………. |
Сделайте вывод о взаимном расположении прямой и окружности, в зависимости от радиуса и расстояния от центра до прямой.
Обсудите свои выводы с товарищем по парте.
Урок закончен.
Приложение 2
Фрагмент урока . 6 класс. Действия с дробями
…Задание 1.
Прочитайте дроби:
1,2; 8/15; 6/7; 0,04; 1целая 2/9; 1,875; 7/4.
Укажите среди них обыкновенные, десятичные дроби. Чем различается запись десятичных и обыкновенных дробей? Что показывает числитель и знаменатель обыкновенной дроби? Какая обыкновенная дробь называется правильной, неправильной?
Обратите данные обыкновенные дроби в десятичные, а десятичные - в обыкновенные:
0,1; 1,6; ½; ¼; 1 целая 1/5; 5.
3. Сравните произведения чисел
1/5 * 0,4; -1/5 * 0,2; 2 целая ½ * 2,25.
Назовите числа, обратные и противоположные данным:
5/7; 4/13; 1 целая 1/3; 0,3; 12; 1,05.
Чему равна сумма противоположных чисел? Чему равно произведение взаимно – обратных чисел?
Сравните с единицей сумму дробей:
¼+1/4+1/4; 1/10+0,2 + ½.
Фронтальная работа класса продолжается в ходе составления карты путешествия.
Составление карты идет так же, как игра в лото. На доске укреплен лист ватмана, разделенный на шесть равных частей. На каждой части крупно нарисовано число (оно будет фигурировать в ответах к математическому лото). А на столе учителя лежат тыльной стороной шесть квадратов таких же по размеру, как и квадраты на вывешенном разграфленном листе. На каждом квадрате с лицевой стороны нарисован участок карты, а на тыльной - одно из шести чисел, изображенных на разграфленном листе.
Задание 2.
Математическое лото. Выполните действия:
А) - 1/10 + 0,5; Б) -2: (-0,2);
В) 0,4 * 2 целых1/2; Г) -1 целая ½ - 10/5;
Д) 3 целых ½ - 0,5; Е) -1/3: 0,2.
Учащиеся выполняют задания, а затем учитель медленно объявляет ответы. Тот, кто первым объявил, что в его работе есть правильный ответ, выходит к доске.
Учитель дает ему квадрат, на одной стороне которого зафиксирован правильный ответ, а на другой нарисована часть карты. Ученик прикрепляет этот квадрат (Рисунком наружу) на большой лист. Карта состоит из 6 квадратов: цветочная поляна с тремя дорогами, озеро, мельница, пещера, снова цветочная поляна и дракон. Звучит куплет из «Бременских музыкантов»:
Ничего на свете лучше нету,
Чем бродить друзьям по белу свету.
Тем, кто дружен, не страшны тревоги.
Нам любые дороги дороги,
Нам любые дороги дороги.
Объявляю, что путешествие начинается с цветочной поляны. Красота цветов обманчива. Среди них могут быть и ядовитые и целебные. Задача - не ошибиться при сборе букета.
Задание 3.
На доске нарисованы цветы, на лепестках написаны дроби. Эти дроби