ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1051
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– арифметическую прогрессию. Найдите знаменатель геометрической прогрессии.
1) –2; 2) –1; 3) –3; 4) –5; 5) –4.
3. Числовая последовательность 1; 8; 22; 43; … обладает таким свойством, что разности двух соседних членов составляют арифметическую прогрессию 7; 14; 21; … . Какой член данной последовательности равен 35351?
1) 97; 2) 99; 3) 101; 4) 103; 5) 107.
К а р т о ч к а № 7.
1. Укажите натуральное число, равное суммы всех предшествующих ему натуральных нечетных чисел.
1) 18; 2) 30; 3) 24; 4) 36; 5) 48.
2. Если к первым четырем членам геометрической прогрессии прибавить соответственно 1, 1, 4 и 18, то получится арифметическая прогрессия. Найдите знаменатель геометрической прогрессии.
1) 2; 2) –2; 3) 3; 4) –3; 5) 4.
3. В последовательности, состоящей из натуральных чисел, второй член больше первого, а каждый член последовательности, начиная с третьего, является произведением двух предыдущих. Если четвертый член равен 18, то чему равна разность между вторым и первым членами последовательности?
1) 1; 2) 5; 3) 17; 4) 1 или 17; 5) 7.
К а р т о ч к а № 8.
1. Укажите натуральное число, равное суммы всех предшествующих ему натуральных нечетных чисел.
1) 68; 2) 24; 3) 32; 4) 64; 5) 40.
2. Последовательность (ап) задана рекуррентной формулой а1 = 0,
а2 = 1, … ап + 2 = ап + 1 – ап. Найдите 885-й член этой последовательности.
1) 1; 2) 0; 3) –1; 4) 2; 5) 3.
3. В последовательности, состоящей из натуральных чисел, первый член выбирается случайным образом, а каждый последующий член последовательности получается возведением предыдущего в квадрат и вычитанием из результата 5. Если третий член равен 116, то чему равен первый член последовательности?
1) 3; 2) 4; 3) 5; 4) 7; 5) 8.
О т в е т ы:
2. Остальные учащиеся разбирают свои ошибки в группах (создаются 2 группы). Раздать учащимся шаблоны с правильным решением подобных задач из контрольной работы. Учащиеся сами выбирают нужную карточку и, используя ее, решают ошибочное задание. Исправив ошибочное решение, ученик выходит к доске и показывает правильное решение всему классу. После окончания этой работы ученики могут приступать к решению заданий по карточкам.
III. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что такое последовательность? Какие способы задания последовательности существуют?
– Сформулируйте определение арифметической прогрессии. Какое число называется разностью арифметической прогрессии?
– Сформулируйте определение геометрической прогрессии. Какое число называется знаменателем геометрической прогрессии?
– Запишите формулы п-го члена и суммы первых п членов для арифметической и геометрической прогрессий.
Домашнее задание: № 675, № 686, № 709, № 660.
У р о к 71 Дата:
КОМБИНАТОРНЫЕ ЗАДАЧИ.
КОМБИНАЦИИ С УЧЕТОМ И БЕЗ УЧЕТА ПОРЯДКА
Цели: ввести понятие комбинаторной задачи, рассмотреть задачи с учетом и без учета порядка; формировать умения решать комбинаторные задачи полным перебором вариантов, а также с помощью графов.
Ход урока
I. Организационный момент.
II. Устная работа.
Решить старинную задачу VIII века:
ВОЛК, КОЗА И КАПУСТА
Некий человек должен был перевезти в лодке через реку волка, козу и капусту. В лодке мог поместиться только один человек, а с ним или волк, или коза, или капуста. Но если оставить волка с козой без человека, то волк съест козу, если оставить козу с капустой, то коза съест капусту, а в присутствии человека никто никого не ест. Как перевезти груз через реку?
При решении этой задачи учащиеся комбинируют разные сочетания, оценивают варианты, получают следующее решение:







III. Объяснение нового материала.
1. В математике существует немало задач, в которых требуется из имеющихся элементов составить различные наборы, подсчитать количество всевозможных комбинаций элементов, образованных по определенному правилу. Такие задачи называются комбинаторными, а раздел математики, занимающейся решением этих задач, называется комбинаторикой (от лат. combinare, которое означает «соединять, сочетать»).
С комбинаторными задачами люди имели дело еще в глубокой древности, когда, например, они выбирали наилучшее расположение воинов во время охоты, придумывали узоры на одежде или посуде. Позже появились нарды, шахматы. Как ветвь математики комбинаторика возникла только в XVII в. В дальнейшем полем для приложения комбинаторных методов оказались биология, химия, физика. И, наконец, роль комбинаторики коренным образом изменилась с применением компьютеров: она превратилась в область, находящуюся на магистральном пути развития науки.
2. П р и м е р ы к о м б и н а т о р н ы х з а д а ч.
Рассмотрим примеры, разобранные на с. 171–172 учебника. При этом обратим внимание учащихся, что в первой задаче в комбинациях нам не важен порядок элементов, а во второй задаче порядок элементов следует учитывать.
Способ рассуждений, которым мы воспользовались при решении этих задач, называется перебором возможных вариантов. Смысл этих упражнений в том, чтобы показать учащимся преимущества организованного, систематического перебора вариантов. Не нужно перечислять числа произвольно, по принципу «что придет на ум». Нужна система: фиксируем один элемент и начинаем перебирать оставшиеся, анализируем и т. д.
Демонстрируем ученикам преимущества наглядного представления комбинаций с помощью графов – полных либо графа-дерева.
IV. Формирование умений и навыков.
На этом уроке при решении задач следует особое внимание уделить анализу условий: является ли задача на комбинацию с учетом или без учета порядка элементов, как удобнее изобразить решение: с помощью графа или простым перечислением (полным перебором).
№ 715.
В этой задаче не учитывается порядок элементов. Можно осуществлять перебор как в примере 1, а можно наглядно переставить в виде графа:
Ребра графа показывают связь в парах, таких ребер 10, значит, всего 10 вариантов выбора подруг.
З а д а ч а. В столовой предлагают два первых блюда: щи и борщ; три вторых блюда: рыба, гуляш и плов; два третьих: компот и чай. Перечислите все возможные варианты обедов из трех блюд. Проиллюстрируйте ответ, построив дерево возможных вариантов.
Р е ш е н и е
1) –2; 2) –1; 3) –3; 4) –5; 5) –4.
3. Числовая последовательность 1; 8; 22; 43; … обладает таким свойством, что разности двух соседних членов составляют арифметическую прогрессию 7; 14; 21; … . Какой член данной последовательности равен 35351?
1) 97; 2) 99; 3) 101; 4) 103; 5) 107.
К а р т о ч к а № 7.
1. Укажите натуральное число, равное суммы всех предшествующих ему натуральных нечетных чисел.
1) 18; 2) 30; 3) 24; 4) 36; 5) 48.
2. Если к первым четырем членам геометрической прогрессии прибавить соответственно 1, 1, 4 и 18, то получится арифметическая прогрессия. Найдите знаменатель геометрической прогрессии.
1) 2; 2) –2; 3) 3; 4) –3; 5) 4.
3. В последовательности, состоящей из натуральных чисел, второй член больше первого, а каждый член последовательности, начиная с третьего, является произведением двух предыдущих. Если четвертый член равен 18, то чему равна разность между вторым и первым членами последовательности?
1) 1; 2) 5; 3) 17; 4) 1 или 17; 5) 7.
К а р т о ч к а № 8.
1. Укажите натуральное число, равное суммы всех предшествующих ему натуральных нечетных чисел.
1) 68; 2) 24; 3) 32; 4) 64; 5) 40.
2. Последовательность (ап) задана рекуррентной формулой а1 = 0,
а2 = 1, … ап + 2 = ап + 1 – ап. Найдите 885-й член этой последовательности.
1) 1; 2) 0; 3) –1; 4) 2; 5) 3.
3. В последовательности, состоящей из натуральных чисел, первый член выбирается случайным образом, а каждый последующий член последовательности получается возведением предыдущего в квадрат и вычитанием из результата 5. Если третий член равен 116, то чему равен первый член последовательности?
1) 3; 2) 4; 3) 5; 4) 7; 5) 8.
О т в е т ы:
| № карточки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1-е задание | 5 | 4 | 4 | 3 | 1 | 4 | 3 | 3 |
| 2-е задание | 1 | 3 | 1 | 2 | 2 | 1 | 1 | 1 |
| 3-е задание | 2 | 1 | 1 | 1 | 4 | 3 | 1 | 2 |
2. Остальные учащиеся разбирают свои ошибки в группах (создаются 2 группы). Раздать учащимся шаблоны с правильным решением подобных задач из контрольной работы. Учащиеся сами выбирают нужную карточку и, используя ее, решают ошибочное задание. Исправив ошибочное решение, ученик выходит к доске и показывает правильное решение всему классу. После окончания этой работы ученики могут приступать к решению заданий по карточкам.
III. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что такое последовательность? Какие способы задания последовательности существуют?
– Сформулируйте определение арифметической прогрессии. Какое число называется разностью арифметической прогрессии?
– Сформулируйте определение геометрической прогрессии. Какое число называется знаменателем геометрической прогрессии?
– Запишите формулы п-го члена и суммы первых п членов для арифметической и геометрической прогрессий.
Домашнее задание: № 675, № 686, № 709, № 660.
У р о к 71 Дата:
КОМБИНАТОРНЫЕ ЗАДАЧИ.
КОМБИНАЦИИ С УЧЕТОМ И БЕЗ УЧЕТА ПОРЯДКА
Цели: ввести понятие комбинаторной задачи, рассмотреть задачи с учетом и без учета порядка; формировать умения решать комбинаторные задачи полным перебором вариантов, а также с помощью графов.
Ход урока
I. Организационный момент.
II. Устная работа.
Решить старинную задачу VIII века:
ВОЛК, КОЗА И КАПУСТА
Некий человек должен был перевезти в лодке через реку волка, козу и капусту. В лодке мог поместиться только один человек, а с ним или волк, или коза, или капуста. Но если оставить волка с козой без человека, то волк съест козу, если оставить козу с капустой, то коза съест капусту, а в присутствии человека никто никого не ест. Как перевезти груз через реку?
При решении этой задачи учащиеся комбинируют разные сочетания, оценивают варианты, получают следующее решение:






III. Объяснение нового материала.
1. В математике существует немало задач, в которых требуется из имеющихся элементов составить различные наборы, подсчитать количество всевозможных комбинаций элементов, образованных по определенному правилу. Такие задачи называются комбинаторными, а раздел математики, занимающейся решением этих задач, называется комбинаторикой (от лат. combinare, которое означает «соединять, сочетать»).
С комбинаторными задачами люди имели дело еще в глубокой древности, когда, например, они выбирали наилучшее расположение воинов во время охоты, придумывали узоры на одежде или посуде. Позже появились нарды, шахматы. Как ветвь математики комбинаторика возникла только в XVII в. В дальнейшем полем для приложения комбинаторных методов оказались биология, химия, физика. И, наконец, роль комбинаторики коренным образом изменилась с применением компьютеров: она превратилась в область, находящуюся на магистральном пути развития науки.
2. П р и м е р ы к о м б и н а т о р н ы х з а д а ч.
Рассмотрим примеры, разобранные на с. 171–172 учебника. При этом обратим внимание учащихся, что в первой задаче в комбинациях нам не важен порядок элементов, а во второй задаче порядок элементов следует учитывать.
Способ рассуждений, которым мы воспользовались при решении этих задач, называется перебором возможных вариантов. Смысл этих упражнений в том, чтобы показать учащимся преимущества организованного, систематического перебора вариантов. Не нужно перечислять числа произвольно, по принципу «что придет на ум». Нужна система: фиксируем один элемент и начинаем перебирать оставшиеся, анализируем и т. д.
Демонстрируем ученикам преимущества наглядного представления комбинаций с помощью графов – полных либо графа-дерева.
IV. Формирование умений и навыков.
На этом уроке при решении задач следует особое внимание уделить анализу условий: является ли задача на комбинацию с учетом или без учета порядка элементов, как удобнее изобразить решение: с помощью графа или простым перечислением (полным перебором).
№ 715.
В этой задаче не учитывается порядок элементов. Можно осуществлять перебор как в примере 1, а можно наглядно переставить в виде графа:
| В – Вера З – Зоя М – Марина П – Полина С – Светлана | 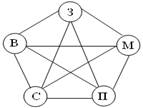 |
Ребра графа показывают связь в парах, таких ребер 10, значит, всего 10 вариантов выбора подруг.
З а д а ч а. В столовой предлагают два первых блюда: щи и борщ; три вторых блюда: рыба, гуляш и плов; два третьих: компот и чай. Перечислите все возможные варианты обедов из трех блюд. Проиллюстрируйте ответ, построив дерево возможных вариантов.
Р е ш е н и е
| Первое блюдо | | Второе блюдо | | Третье блюдо | Варианты обеда |
| |  | | | | щ – р – к (1) |
| | щ – р – ч (2) | ||||
| | | | | щ – г – к (3) | |
| | щ – г – ч (4) | ||||
| | | | | щ – п – к (5) | |
| | щ – п – ч (6) | ||||
| |  | | | | б – р – к (7) |
| | б – р – ч (8) | ||||
| | | | | б – г – к (9) | |
| | б – г – ч (10) | ||||
| | | | | б – п – к (11) | |
| | б – п – ч (12) |