ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1053
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
О т в е т: 12 вариантов.
№ 716.
В этой задаче при выборе пар входов порядок выбора имеет значение: АВ означает, что посетитель вошел через А, а вышел через В, а ВА означает, что вошел через В, а вышел через А.
Фиксируем каждый вход по очереди и дописываем к нему в пару оставшиеся:
А: АВ, АС, АD;
В: ВА, ВС, ВD;
С: СА, СВ, СD;
D: DA, DB, DC.
Итого – 12 вариантов.
№. 718, № 720. При решении этих задач следует обратить внимание учащихся, что если мы из цифр составляем двузначное (трехзначное) число, то нуль не может стоять на первом месте.
№ 717. Заметим, что для указания способа раскладки яблок в две вазы достаточно указать способ заполнения одной вазы, поскольку все, что не попадает в первую вазу, попадает во вторую.
Вообще, во всех случаях, когда п элементов нужно разбить на 2 группы, при подсчете количества способов разбиения достаточно подсчитать число способов формирования одной половины.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какие задачи называются комбинаторными?
– Приведите примеры ситуаций выбора комбинаций с учетом и без учета порядка элементов.
– В чем сущность способа полного перебора вариантов?
– Из чего состоит граф (граф-дерево) возможных вариантов?
Домашнее задание: № 714, № 719, № 721, № 729
У р о к 72 Дата:
КОМБИНАТОРНОЕ ПРАВИЛО УМНОЖЕНИЯ
Цели: изучить комбинаторное правило умножения; формировать умения решать комбинаторные задачи с помощью правила умножения и составления таблиц возможных вариантов.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Три друга при встрече обменялись рукопожатиями. Сколько всего было сделано рукопожатий? (3.)
2. Есть помидоры, огурцы и лук. Сколько различных салатов можно приготовить, если в каждый из них должны входить в равных долях 2 различных вида овощей? (3.)
3. Перечислить все возможные способы разложения по двум вазам одного яблока и одной груши. (4.)
4. Сколькими способами Петя и Вова могут занять 2 места за одной двухместной партой? (2.)
5. Сколько подарочных наборов можно составить:
1) из одного предмета; (1.)
2) из двух предметов, если в наличии имеются одна ваза и одна ветка сирени? (3.)
III. Объяснение нового материала.
1. Чтобы подвести учащихся к «открытию» комбинаторного правила умножения, целесообразно начать объяснение нового материала с проверки решения задачи № 714 (домашнее задание) с выносом графа-дерева решения на доску:
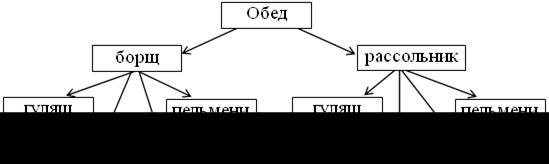
Замечаем, что можно было решить эту задачу даже устно. Рассуждаем так. Первое блюдо можно выбрать двумя способами. Для каждого первого блюда можно подобрать второе четырьмя способами. Эти выборы независимы друг от друга, так как каждый осуществляется из своего множества вариантов. Значит, общее число вариантов обеда равно произведению 2 · 4, то есть 8.
В о п р о с у ч а щ и м с я: а если бы на обед было предложено выбрать еще одно третье блюдо из пяти: чай, кофе, сок, компот, кисель? Тогда для каждого варианта обеда мы могли бы предложить пять вариантов третьего блюда и получили бы 8 · 5 или 40 вариантов обеда из трех блюд.
2. Решая эту задачу, мы использовали так называемое комбинаторное правило умножения.
Формулируем его в общем виде, обращая особое внимание на условие его применения – выбор из независимых наборов вариантов:
Пусть имеется п элементов и требуется выбрать из них один за другим k элементов. Если первый элемент можно выбрать п1 способами, после чего второй элемент можно выбрать п2 способами из оставшихся, затем третий элемент можно выбрать п3 способами из оставшихся и т. д., то число способов, которыми могут быть выбраны все k элементов, равно произведению п1 · п2 · п2 · … · пk.
3. П р и м е р 3 рассматриваем из учебника со с. 173.
IV. Формирование умений и навыков.
На прошлом уроке мы рассмотрели два способа решения комбинаторных задач:
1. Перечисление (полный перебор) вариантов.
2. Подсчет вариантов с помощью графов.
2.1. Полные графы.
2.2. Дерево возможных вариантов (граф-дерево).
На этом уроке добавляются еще два способа:
3. Составление таблицы возможных вариантов.
4. Непосредственное применение комбинаторного правила умножения.
Упражнения:
№ 727, № 728. На непосредственное применение комбинаторного правила умножения.
О б р а з е ц о ф о р м л е н и я решения задачи.
№ 728.
В задаче 4 последовательных выбора, каждый из своего множества вариантов. Общее количество различных карнавальных костюмов равно:
5 · 6 · 3 · 2 = 180.
О т в е т: 180 различных костюмов.
№ 722.
Выбирая команды для игры, мы не учитываем порядок в паре, так как если первая команда играла со второй, то это одновременно означает, что вторая команда играла с первой.
Составим таблицу возможных вариантов, отмечая крестиком игру между командами.
| Команда | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 2 3 4 5 6 7 8 9 10 11 12 |  | |||||||||||
Можно просто посчитать количество крестиков, но это не рационально. Заметим, что количество игр представляет собой арифметическую прогрессию (ап), где а1 = 1, d = 1, п = 11. Значит, нам надо найти S11.
Это мы посчитали количество игр, проведенных командами на своем поле. Значит, столько же игр сыграно на поле противника. Итого – 132 игры.
№ 723.
На прошлом уроке мы решали такую же задачу, но с меньшим количеством участников, с помощью графа. В этой задаче этот способ применять нецелесообразно, так как очень большое количество ребер графа может только запутать учеников. Покажем два других способа решения этой задачи.
I с п о с о б. Составление таблицы возможных вариантов.
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 |  | |||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 | ||||||||
| 5 | ||||||||
| 6 | ||||||||
| 7 | ||||||||
| 8 | ||||||||
(ап) – арифметическая прогрессия.
а1 = 1, d = 1, п = 7;
О т в е т: 28 рукопожатий.
II с п о с о б. Применение комбинаторного правила умножения.
Каждый человек пожимает руку семи оставшимся. Но так как порядок выбора не имеет значения (если Иванов пожимает руку Петрову, то одновременно и Петров пожимает руку Иванову), то общее число рукопожатий равно = 28.
О т в е т: 28 рукопожатий.
№ 725. Применение комбинаторного правила умножения.
Всего 10 цифр, каждая цифра комбинируется с оставшимися девятью (причем важен порядок, так как 2–3 и 3–2 разные коды) и с самой собой (возможен код 1–1, 3–3 и т. д.). Значит, вариантов 10 · 10 = 100. Так как в доме 96 квартир, то кодов хватит для всех.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какие способы решения комбинаторных задач вы знаете?
– Охарактеризуйте каждый способ решения.
– Сформулируйте комбинаторное правило умножения.
Домашняя работа: № 724, № 726, № 834, № 730 (а), № 731 (в).
У р о к 73 Дата:
ПЕРЕСТАНОВКА ИЗ п ЭЛЕМЕНТОВ
КОНЕЧНОГО МНОЖЕСТВА
Цели: ввести понятие перестановки из п элементов конечного множества, понятие п!; вывести формулу нахождения числа перестановок с помощью комбинаторного правила умножения и формировать умение ее применения при решении задач.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Подсчитать число однобуквенных слов русского языка.
Р е ш е н и е
| а – союз б – сокращенное частицы «бы» в – предлог ж – сокращенное частицы «же» и – союз к – предлог | о – предлог с – предлог у – предлог и междометие э – междометие я – местоимение |
З а м е ч а н и е: смысл упражнения в том, чтобы напомнить учащимся преимущества организованного, систематического перебора вариантов. Не перечисляем произвольно однобуквенные слова, а берем алфавит, просматриваем буквы и анализируем, употребляется ли эта буква как самостоятельное слово или нет.