ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1049
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= = –364.
О т в е т: –364.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– По каким формулам находят сумму первых п членов геометрической прогрессии?
– Какие ограничения накладываются на выражения в формулах?
– Как находится сумма первых п членов геометрической прогрессии со знаменателем, равным 1?
Домашнее задание: № 649 (б, в), № 650, № 652 (а, г), № 656, № 659 (а).
У р о к 68 Дата:
ПРИМЕНЕНИЕ ФОРМУЛЫ СУММЫ ПЕРВЫХ п ЧЛЕНОВ
ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ
Цели: закреплять умения и навыки применения формулы суммы первых п членов геометрической прогрессии при решении задач; провести подготовку к контрольной работе.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Вычислить:
а) 32п : 9п – 1; (9.)
б) 4п · 26 – 2п; (64.)
в) 16 : 41 + 2п · 8п. (22 – п.)
2. Является ли геометрической прогрессией последовательность (хп), если:
а) хп = 2п; (Да.)
б) хп = 3–п; (Да.)
в) хп = п2; (Нет.)
г) хп = a · bn, если а ¹ 0, b ¹ 0. (Да.)
3. Существуют ли три числа, которые составляют одновременно арифметическую и геометрическую прогрессию? (Да, любые три равных числа.)
III. Формирование умений и навыков.
На этом уроке предлагаются для решения упражнения на нахождение суммы первых п членов геометрической прогрессии по двум формулам, а также задания на применение формулы п-го члена и характеристического свойства геометрической прогрессии, в том числе повышенной сложности. Перед решением следует вспомнить определение геометрической прогрессии и все формулы
, относящиеся к ней.
Упражнения:
1. № 635.
Р е ш е н и е
(хп) – геометрическая прогрессия.
(хп) : 2; а; b; ;
;
;
.
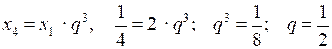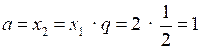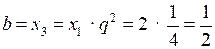О т в е т: а = 1; b = .
№ 640.
Р е ш е н и е
(хп) – геометрическая прогрессия.
х1 = 760;
q = 0,8, так как после каждого движения поршня удаляется 20 % воздуха, значит, остается 80 %. Давление после шести движений поршня равно х7 = х1 · q6; х7 = 760 · (0,8)6 ≈ 199,23.
О т в е т: ≈ 199,23 мм рт. ст.
2. С а м о с т о я т е л ь н а я р а б о т а (с последующей проверкой на этом же уроке).
В а р и а н т 1
1) Найдите сумму пяти первых членов геометрической прогрессии (bn), в которой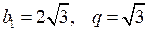
.
2) Найдите сумму шести первых членов геометрической прогрессии 5; –2,5; … .
3) (ап) – геометрическая прогрессия. Найдите S4, если а1 = 3, q = –2.
4) Найдите первый член геометрической прогрессии, в которой q = , S4 = 65.
В а р и а н т 2
1) Найдите сумму шести первых членов геометрической прогрессии (bn), в которой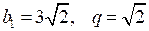
.
2) Найдите сумму пяти первых членов геометрической прогрессии 1,5; –3; … .
3) (aп) – геометрическая прогрессия. Найдите S5, если а1 = 18, q = – .
4) Найдите первый член геометрической прогрессии, в которой q = 2, S8 = 765.
Р е ш е н и я самостоятельной работы
В а р и а н т 1
1)
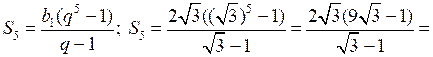
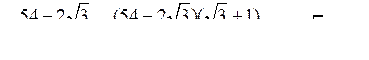
2)
;
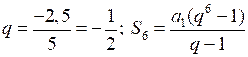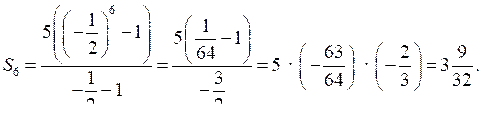
3)
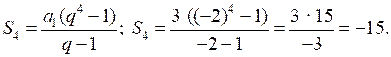
4)
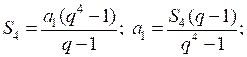
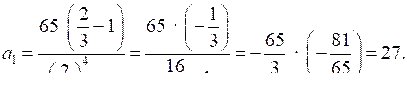
В а р и а н т 2
1)
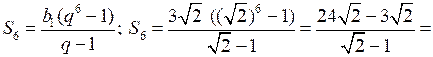
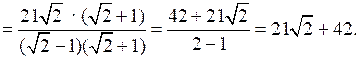
2)
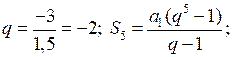
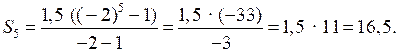
3)
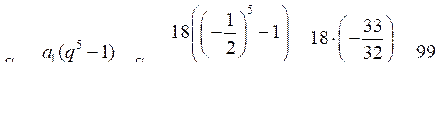
4)
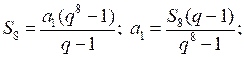
3. З а д а н и я п о в ы ш е н н о й с л о ж н о с т и.
№ 657.
Д а н о: (хп) – геометрическая прогрессия.
хп > 0 для любого n N;
х1 + х2 = 8; х3 + х4 = 72; Sk = 242.
Н а й т и: k.
Р е ш е н и е
Пусть q – знаменатель прогрессии и q > 0 (так как хп > 0), тогда по определению хп = х1 · qп – 1. По условию
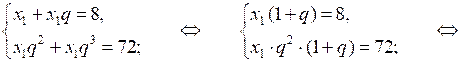
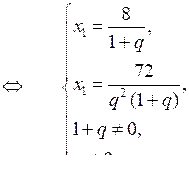
Получаем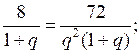
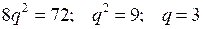(так как q > 0).
Находим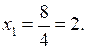
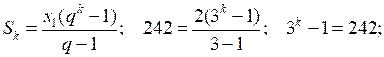
3k= 243; 3k= 35; k = 5.
О т в е т: 5 членов.
З а д а ч а. Сумма трех первых членов геометрической прогрессии равна 13, а сумма их квадратов равна 91. Найдите первый член прогрессии, ее знаменатель и сумму пяти первых членов.
Р е ш е н и е
Пусть a, b, c – первые члены геометрической прогрессии. По свойству геометрической прогрессии имеем b2 = ac. Учитывая условия задачи, запишем следующую систему уравнений с тремя неизвестными:
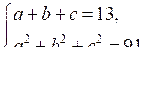
Из первого уравнения a + c = 13 – b. Возведем обе части уравнения в квадрат, получим:
a2 + 2ac + c2 = 169 – 26b + b2 (1);
из второго уравнения a2 + c2 = 91 – b2. Подставляем в уравнение (1) и получаем:
91 – b2 + 2b2 = 169 – 26b + b2,
26b = 78,
b = 3.
Подставляем значение b = 3 в исходную систему и получаем:
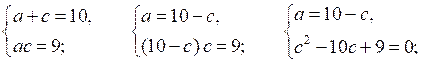
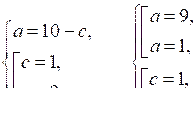
Таким образом, первые три члена последовательности 1; 3; 9 (q = 3) или 9; 3; 1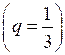
.
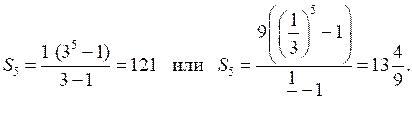
О т в е т: 1; 3; 121 или 9;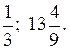
Задачи повышенной сложности можно решать следующим образом: разобрать идею решения, составить исходную систему уравнений, а ее решение предложить выполнить самостоятельно дома. Или сильным в учебе ученикам предложить решить в классе, а с более слабыми учениками продолжить отрабатывать основные формулы по стандартным упражнениям из сборника самостоятельных работ.
IV. Итоги урока.
Ответить на контрольные вопросы (учебник, с. 163).
Домашнее задание: № 636, № 658, № 710.
У р о к 69 Дата:
КОНТРОЛЬНАЯ РАБОТА № 5
В а р и а н т 1
1. Найдите седьмой член геометрической прогрессии (bп), если b1 = –32 и q = .
2. Первый член геометрической прогрессии (bп) равен 2, а знаменатель равен 3. Найдите сумму шести первых членов этой прогрессии.
3. Между числами и 3 вставьте три числа, которые вместе с данными числами образуют геометрическую прогрессию.
4. Найдите сумму девяти первых членов геометрической прогрессии (bп) с положительными членами, зная, что b2 = 0,04 и b4 = 0,16.
5. Найдите первый член геометрической прогрессии (ап), в которой q = 3, S4 = 560.
В а р и а н т 2
1. Найдите шестой член геометрической прогрессии (bп), если b1 = 0,81 и q = .
2. Первый член геометрической прогрессии (bп) равен 6, а знаменатель равен 2. Найдите сумму семи первых членов этой прогрессии.
3. Между числами и 196 вставьте три числа так, чтобы они вместе с данными числами составили геометрическую прогрессию.
4. Найдите сумму восьми первых членов геометрической прогрессии (bп) с положительными членами, зная, что b2 = 1,2 и b4 = 4,8.
5. Найдите первый член геометрической прогрессии (ап), в которой q = –2, S5 = 330.
В а р и а н т 3
1. Найдите пятый член геометрической прогрессии (bп), если b1 = –125 и q = .
2. Первый член геометрической прогрессии (bп) равен 4, а знаменатель равен 2. Найдите сумму восьми первых членов этой прогрессии.
3. Между числами 48 и вставьте три числа так, чтобы вместе с данными они составили геометрическую прогрессию.
4. Найдите сумму восьми первых членов геометрической прогрессии (bп) с положительными членами, зная, что b3 = 0,05 и b5 = 0,45.
5. Найдите первый член геометрической прогрессии (ап), в которой q = –3, S4 = 400.
В а р и а н т 4
1. Найдите девятый член геометрической прогрессии (bп), если
b1 = 100000 и q = .
2. Первый член геометрической прогрессии (
О т в е т: –364.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– По каким формулам находят сумму первых п членов геометрической прогрессии?
– Какие ограничения накладываются на выражения в формулах?
– Как находится сумма первых п членов геометрической прогрессии со знаменателем, равным 1?
Домашнее задание: № 649 (б, в), № 650, № 652 (а, г), № 656, № 659 (а).
У р о к 68 Дата:
ПРИМЕНЕНИЕ ФОРМУЛЫ СУММЫ ПЕРВЫХ п ЧЛЕНОВ
ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ
Цели: закреплять умения и навыки применения формулы суммы первых п членов геометрической прогрессии при решении задач; провести подготовку к контрольной работе.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Вычислить:
а) 32п : 9п – 1; (9.)
б) 4п · 26 – 2п; (64.)
в) 16 : 41 + 2п · 8п. (22 – п.)
2. Является ли геометрической прогрессией последовательность (хп), если:
а) хп = 2п; (Да.)
б) хп = 3–п; (Да.)
в) хп = п2; (Нет.)
г) хп = a · bn, если а ¹ 0, b ¹ 0. (Да.)
3. Существуют ли три числа, которые составляют одновременно арифметическую и геометрическую прогрессию? (Да, любые три равных числа.)
III. Формирование умений и навыков.
На этом уроке предлагаются для решения упражнения на нахождение суммы первых п членов геометрической прогрессии по двум формулам, а также задания на применение формулы п-го члена и характеристического свойства геометрической прогрессии, в том числе повышенной сложности. Перед решением следует вспомнить определение геометрической прогрессии и все формулы
, относящиеся к ней.
Упражнения:
1. № 635.
Р е ш е н и е
(хп) – геометрическая прогрессия.
(хп) : 2; а; b; ;
; ; .О т в е т: а = 1; b = .
№ 640.
Р е ш е н и е
(хп) – геометрическая прогрессия.
х1 = 760;
q = 0,8, так как после каждого движения поршня удаляется 20 % воздуха, значит, остается 80 %. Давление после шести движений поршня равно х7 = х1 · q6; х7 = 760 · (0,8)6 ≈ 199,23.
О т в е т: ≈ 199,23 мм рт. ст.
2. С а м о с т о я т е л ь н а я р а б о т а (с последующей проверкой на этом же уроке).
В а р и а н т 1
1) Найдите сумму пяти первых членов геометрической прогрессии (bn), в которой
.2) Найдите сумму шести первых членов геометрической прогрессии 5; –2,5; … .
3) (ап) – геометрическая прогрессия. Найдите S4, если а1 = 3, q = –2.
4) Найдите первый член геометрической прогрессии, в которой q = , S4 = 65.
В а р и а н т 2
1) Найдите сумму шести первых членов геометрической прогрессии (bn), в которой
.2) Найдите сумму пяти первых членов геометрической прогрессии 1,5; –3; … .
3) (aп) – геометрическая прогрессия. Найдите S5, если а1 = 18, q = – .
4) Найдите первый член геометрической прогрессии, в которой q = 2, S8 = 765.
Р е ш е н и я самостоятельной работы
В а р и а н т 1
1)
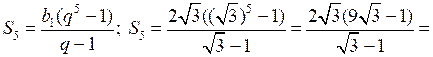
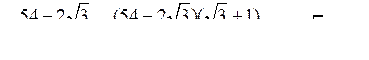
2)
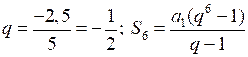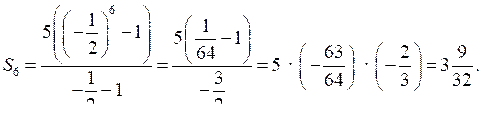
; 3)
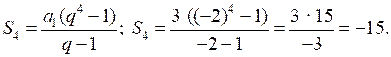
4)
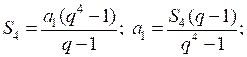
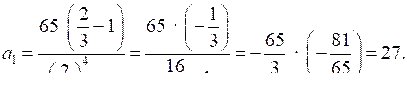
В а р и а н т 2
1)
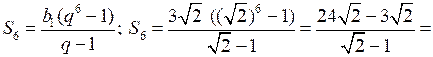
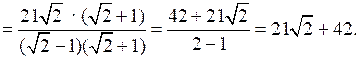
2)
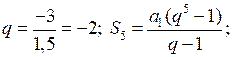
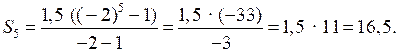
3)
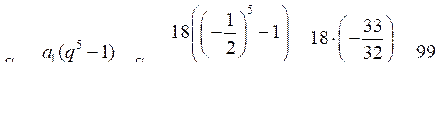
4)
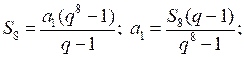
3. З а д а н и я п о в ы ш е н н о й с л о ж н о с т и.
№ 657.
Д а н о: (хп) – геометрическая прогрессия.
хп > 0 для любого n N;
х1 + х2 = 8; х3 + х4 = 72; Sk = 242.
Н а й т и: k.
Р е ш е н и е
Пусть q – знаменатель прогрессии и q > 0 (так как хп > 0), тогда по определению хп = х1 · qп – 1. По условию
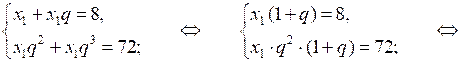
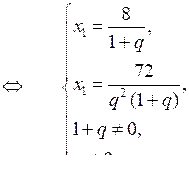
Получаем
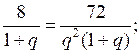
(так как q > 0).Находим
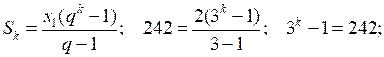
3k= 243; 3k= 35; k = 5.
О т в е т: 5 членов.
З а д а ч а. Сумма трех первых членов геометрической прогрессии равна 13, а сумма их квадратов равна 91. Найдите первый член прогрессии, ее знаменатель и сумму пяти первых членов.
Р е ш е н и е
Пусть a, b, c – первые члены геометрической прогрессии. По свойству геометрической прогрессии имеем b2 = ac. Учитывая условия задачи, запишем следующую систему уравнений с тремя неизвестными:
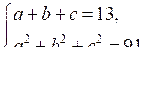
Из первого уравнения a + c = 13 – b. Возведем обе части уравнения в квадрат, получим:
a2 + 2ac + c2 = 169 – 26b + b2 (1);
из второго уравнения a2 + c2 = 91 – b2. Подставляем в уравнение (1) и получаем:
91 – b2 + 2b2 = 169 – 26b + b2,
26b = 78,
b = 3.
Подставляем значение b = 3 в исходную систему и получаем:
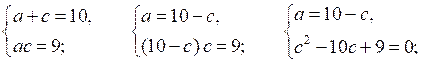
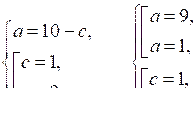
Таким образом, первые три члена последовательности 1; 3; 9 (q = 3) или 9; 3; 1
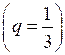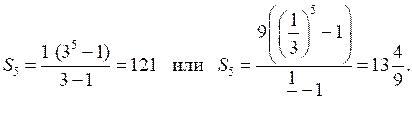
. О т в е т: 1; 3; 121 или 9;
Задачи повышенной сложности можно решать следующим образом: разобрать идею решения, составить исходную систему уравнений, а ее решение предложить выполнить самостоятельно дома. Или сильным в учебе ученикам предложить решить в классе, а с более слабыми учениками продолжить отрабатывать основные формулы по стандартным упражнениям из сборника самостоятельных работ.
IV. Итоги урока.
Ответить на контрольные вопросы (учебник, с. 163).
Домашнее задание: № 636, № 658, № 710.
У р о к 69 Дата:
КОНТРОЛЬНАЯ РАБОТА № 5
В а р и а н т 1
1. Найдите седьмой член геометрической прогрессии (bп), если b1 = –32 и q = .
2. Первый член геометрической прогрессии (bп) равен 2, а знаменатель равен 3. Найдите сумму шести первых членов этой прогрессии.
3. Между числами и 3 вставьте три числа, которые вместе с данными числами образуют геометрическую прогрессию.
4. Найдите сумму девяти первых членов геометрической прогрессии (bп) с положительными членами, зная, что b2 = 0,04 и b4 = 0,16.
5. Найдите первый член геометрической прогрессии (ап), в которой q = 3, S4 = 560.
В а р и а н т 2
1. Найдите шестой член геометрической прогрессии (bп), если b1 = 0,81 и q = .
2. Первый член геометрической прогрессии (bп) равен 6, а знаменатель равен 2. Найдите сумму семи первых членов этой прогрессии.
3. Между числами и 196 вставьте три числа так, чтобы они вместе с данными числами составили геометрическую прогрессию.
4. Найдите сумму восьми первых членов геометрической прогрессии (bп) с положительными членами, зная, что b2 = 1,2 и b4 = 4,8.
5. Найдите первый член геометрической прогрессии (ап), в которой q = –2, S5 = 330.
В а р и а н т 3
1. Найдите пятый член геометрической прогрессии (bп), если b1 = –125 и q = .
2. Первый член геометрической прогрессии (bп) равен 4, а знаменатель равен 2. Найдите сумму восьми первых членов этой прогрессии.
3. Между числами 48 и вставьте три числа так, чтобы вместе с данными они составили геометрическую прогрессию.
4. Найдите сумму восьми первых членов геометрической прогрессии (bп) с положительными членами, зная, что b3 = 0,05 и b5 = 0,45.
5. Найдите первый член геометрической прогрессии (ап), в которой q = –3, S4 = 400.
В а р и а н т 4
1. Найдите девятый член геометрической прогрессии (bп), если
b1 = 100000 и q = .
2. Первый член геометрической прогрессии (