ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1048
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Упражнения:
№ 739.
Р е ш е н и е
Каждое четырехзначное число, составленное из цифр 1; 3; 5; 7 (без повторения), имеет сумму цифр, равную 1 + 3 + 5 + 7 = 16. Из этих цифр можно составить Р4 = 4! = 24 различных числа, отличающихся только порядком цифр. Сумма цифр всех этих чисел равна 16 · 24 = 384.
О т в е т: 384.
№ 740 (а).
Р е ш е н и е
Среди чисел, составленных из цифр 1; 2; 3; 4 (без повторения), больше 3000 будут четырехзначные числа, начинающиеся с цифр 3 или 4.
Фиксируем цифру 3, тогда из оставшихся трех можно получить
Р3 = 3! = 6 перестановок.
Фиксируем цифру 4, тогда из оставшихся трех чисел можно получить Р3 = 6 перестановок. Значит, всего таких чисел 6 + 6 = 12.
О т в е т: 12 чисел.
№ 741.
Р е ш е н и е
а) Всего 7 мальчиков на 7 местах, но один элемент фиксирован, не переставляется (Олег находится в конце ряда). Число комбинаций равно числу перестановок 6 мальчиков, стоящих перед Олегом:
Р6 = 6! = 720.
б) Два элемента фиксированы. Число возможных комбинаций равно числу перестановок 5 мальчиков, стоящих между Олегом и Игорем:
Р5 = 5! = 120.
в) Пусть Олег и Игорь стоят рядом. Возможны два варианта их расположения в паре (Олег – Игорь, Игорь – Олег). Будем рассматривать эту пару как единый элемент, переставляемый с другими пятью элементами. Число таких комбинаций для каждого из двух случаев равно Р6 = 6! = 720. Значит, всего вариантов 720 + 720 = 1440.
З а м е ч а н и е: Такой прием называется «склеиванием» элементов.
О т в е т: а) 720; б) 120; в) 1440.
Также на уроке можно предложить для решения задачи повышенной сложности.
№ 744.
Р е ш е н и е
Применяем прием «склеивания» элементов. Пять сборников стихов можно «склеить» между собой Р5 = 5! = 120 различными способами.
Теперь имеем множество, состоящее из 8 элементов (7 элементов +
+ «склейка»). Для каждой из 120 «склеек» существует Р8 = 8! = 40320 перестановок в группе из 8 элементов. Значит, общее число способов расставить 12 книг, из которых 5 должны стоять рядом, равно 120 · 40320 =
= 4 838 400.
О т в е т: 4 838 400 способов.
№ 745.
Р е ш е н и е
а) 5 мальчиков и 5 девочек могут занять в театре в одном ряду места с 1 по 10-е:
Р10 = 10! = 3 628 800 различными способами.
б) Если мальчики могут сидеть только на нечетных местах, а девочки – только на четных, то мы можем менять местами только мальчиков с мальчиками и девочек с девочками. Для мальчиков это Р5 = 5! = 120 вариантов и Р5 = 120 вариантов – для девочек. Каждый вариант расположения мальчиков может сочетаться с каждым из вариантов расположения девочек, поэтому по комбинаторному правилу умножения общее число способов рассадить детей в этом случае равно 120 · 120 = 14400.
О т в е т: 3 628 800, 14400.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется перестановкой из п элементов? Запишите формулу для вычисления числа перестановок из п элементов.
– Каким способом решаются комбинаторные задачи на перестановки при фиксированных элементах?
– В чем суть приема «склеивания» элементов?
Домашнее задание: № 740 (б), № 742, № 743, № 750.
У р о к 75 Дата:
РАЗМЕЩЕНИЕ ИЗ п ЭЛЕМЕНТОВ ПО k (k ≤ n)
Цели: ввести понятие размещения из п элементов по k, где k ≤ n; вывести формулу нахождения числа размещений с помощью комбинаторного правила умножения; формировать умение решать комбинаторные задачи с применением данной формулы.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Вычислить:
а) ; б)
; в) 
; г) 
.2. Составить всевозможные двухбуквенные слова, используя буквы:
а) ы, т, в (ты; вы); б) н, о, а (но, на, он, ан).
3. Анна (А), Белла (Б) и Вера (В) купили билеты в кинотеатр на 1-е, 2-е и 3-е места первого ряда. Перечислить все возможные способы, которыми девочки могут занять эти три места.
(Р3 = 3! = 6: АБВ, АВБ; БАВ, БВА; ВАБ, ВБА.)
III. Проверка домашнего задания.
С обязательным вынесением на доску решения.
№ 750 (б).
Р е ш е н и е
(п + 1)! · п = п! (п + 1) · п > п! (п + 1) в п раз.
IV. Объяснение нового материала.
1. Для актуализации знаний предложить для решения № 839 (а, б).
Р е ш е н и е
а)
= n + 1;б)
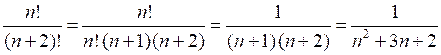.2. З а д а ч а. Из четырех конфет – ириска (и), леденец (л), карамель (к), шоколадная (ш) – Марина решила последовательно съесть три. Перечислите все варианты, которыми это можно сделать.
Это задача о выборе трех элементов из четырех с учетом порядка выбора.
Начинаем перечисление с анализа условия: первую конфету можно выбрать одним из четырех способов; для каждой первой конфеты вторую можно выбрать тремя способами из трех оставшихся; для каждой второй третью конфету можно выбрать двумя способами из двух оставшихся. Мы сразу видим количество вариантов – по правилу умножения их 4 · 3 · 2 = 24 – и алгоритм записи в таблицу (в первой строке комбинации, начинающиеся с «и», во второй – с «л» и т. д.).
| илк | илш | икл | икш | ишл | ишк |
| лик | лиш | лки | лкш | лши | лшк |
| кил | киш | кли | клш | кши | кшл |
| шил | шик | шли | шлк | шки | шкл |
Каждую такую упорядоченную тройку, которую можно составить из четырех элементов, называют размещением из четырех элементов по три.
3. Определение
. Размещением из п элементов по k (k £ n) называется любое множество, состоящее из k элементов, взятых в определенном порядке из данных п элементов.
О б о з н а ч е н и е. (читается «А из п по k»).
Подчеркиваем, что в этом определении важен не только выбор, но и порядок элементов в выборе.
4. Формулу можно вывести по правилу умножения, причем, для частного случая, мы уже знаем алгоритм. Можно сильному классу попробовать вывести самостоятельно:
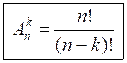– формула вычисления числа размещений из п по k.Очень важный момент при изучении этой формулы – рассмотреть случай, когда п = k. Тогда получается размещения из п элементов по п отличаются друг от друга только порядком элементов, то есть представляют собой перестановки из п элементов.
Будем считать по определению 0! = 1, в этом случае
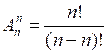, то есть 
.5. Рассмотрим примеры 1 и 2 со с. 181–182 учебника.
V. Формирование умений и навыков.
Упражнения:
№ 754.
Р е ш е н и е
Пронумеруем места в купе (с 1 по 4) и будем «выдавать» каждому из трех членов семьи номер места. Из 4 элементов (номеров мест) будут делаться выборки по 3 элемента, при этом важен не только состав выборки, но и порядок расположения в ней элементов. Число способов равно числу размещений из 4 по 3:
= 2 · 3 · 4 = 24.О т в е т: 24 способа.
№ 756, № 757. Самостоятельное решение с последующей проверкой.
При решении этих заданий следует уделять внимание обоснованию выбора формулы для подсчета числа размещений, не допуская формализма.
Ученики могут решить эти задания не только по формуле, но и применяя комбинаторное правило умножения. Следует поощрять и этот способ решения, так как он позволяет осознать структуру самой формулы и лучше ее запомнить.
№ 760.
Р е ш е н и е
а) Выбираем 2 места для фотографий из 6 свободных мест в альбоме:
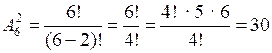.б) Выбираем 4 места для фотографий из 6:
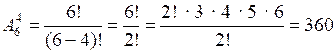.в) Выбираем 6 мест из 6 (делаем всевозможные перестановки из 6 фотографий):
= Р6 = 6! = 1 · 2 · 3 · 4 · 5 · 6 = 720.
О т в е т: а) 30 способов; б) 360 способов; в) 720 способов.
№ 762.
Р е ш е н и е
а) Выбираем 4 цифры из 5 данных, порядок выбора имеет значение:
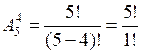= 2 · 3 · 4 · 5 = 120.б) Выбираем 4 цифры из 5, но на первое место нельзя выбирать ноль. Используем метод исключения лишних элементов: если на первое место выбран ноль, то после этого выбираем еще на 3 места цифры из 4 оставшихся, получаем = 2 · 3 · 4 = 24 «нулевых» комбинаций, которые недопустимы.
Количество всех четырехзначных чисел, которые можно составить из данных 5 чисел, равно: = 2 · 3 · 4 · 5 = 120.
Значит, допустимых – = 120 – 24 = 96.
О т в е т: а) 120 чисел; б) 96 чисел.
VI. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется размещением из п элементов по k?
– Запишите формулу для вычисления числа размещений из п элементов по k.
– Чему равно 0!? 1!?
Домашнее задание: № 755, № 758, № 759, № 767.
У р о к 76 Дата:
КОМБИНАТОРНЫЕ ЗАДАЧИ НА НАХОЖДЕНИЕ ЧИСЛА
РАЗМЕЩЕНИЙ ИЗ п ЭЛЕМЕНТОВ ПО k (k ≤ п)
Цель: продолжить формирование умений применять формулу нахождения числа размещений из п элементов по k при решении задач.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Вычислить:
а) ; б) ; в) .
2. Делится ли 50!:
а) на 75; б) 77; в) 159.
3. Имеются три книги трех различных авторов: Толстого Л. Н. (Т); Пушкина А. С. (П); Достоевского Ф. М. (Д). Сколькими способами из этих книг можно расположить на полке:
а) одну книгу; б) две книги; в) три книги?
III. Формирование умений и навыков.
На этом уроке следует решать упражнения не только на прямое применение формулы нахождения числа размещений, но и задачи повышенной сложности, а также задачи, имеющие несколько способов решения.