ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1047
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
№ 761.
Р е ш е н и е
Выбираем 5 букв для обозначения точек из 26 букв в алфавите; порядок выбора имеет значение (какую точку какой буквой обозначим):
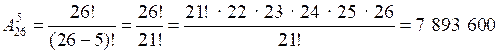.О т в е т: 7 893 600 способов.
№ 763.
Р е ш е н и е
Выбираем из 10 цифр семь, причем первый выбор делается из 9 цифр (без нуля). Используя метод исключения лишних вариантов, получаем:
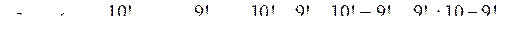
1· 2 · 3 · 4 · 5 · 7 · 8 · 9 · 9 = 544320.О т в е т: 544320.
№ 764.
Р е ш е н и е
Выбираем 3 цифры из 5 данных, причем:
а) последней цифрой должна быть 2 или 4; количество вариантов (фиксирована 2) + (фиксирована 4) = 2 · = 2 · 3 · 4 = = 24.
б) последней цифрой должна быть 5; количество вариантов равно (фиксирована 5) = = 3 · 4 = 12.
О т в е т: а) 24 числа; б) 12 чисел.
Прежде чем приступить к самостоятельной работе, можно решить два задания повышенной сложности с факториалами.
№ 837.
Р е ш е н и е
Число оканчивается одним нулем, если среди множителей, на которые оно разлагается, есть одно число 10; оканчивается двумя нулями, если есть два множителя 10; и тремя нулями – если есть три множителя 10.
Поскольку п! есть произведение п последовательных натуральных чисел, то в нем каждый второй множитель четный, то есть содержит в разложении число 2, а каждый пятый множитель кратен 5. Поэтому каждый пятый множитель в п! добавляет в разложение этого числа одно число 10.
Таким образом,
а) 5! содержит двойки и одну 5, что дает один множитель 10, то есть 5! заканчивается одним нулем;
б) 10! содержит двойки и две 5, что дает два множителя 10, то есть 10! оканчивается двумя нулями;
в) 15! содержит двойки и три 5, что дает три множителя 10, то есть 15! оканчивается тремя нулями.
О т в е т: а) 5!; б) 10!; в) 15!
№ 840.
Р е ш е н и е
а)
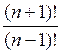= 42;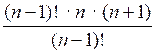 
= 42;
п · (п + 1) = 42; п = 6.
З а м е ч а н и е: квадратное уравнение можно не решать, так как второй корень не будет натуральным числом.
б)
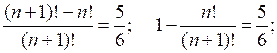
О т в е т: а) п = 6; б) п = 5.
IV. Самостоятельная работа.
В а р и а н т 1
1. Сколькими способами пять школьников, сдающих экзамен, могут занять места в классе, в котором стоят 20 одноместных столов?
2. Решить уравнение:
п! = 7 (п – 1)!.
3. Сколькими нулями оканчивается число 12!?
В а р и а н т 2
1. Сколькими способами семь малышей могут занять места в комнате детского сада, в которой стоит 18 детских стульчиков?
2. Решить уравнение:
п! = 12 (п – 1)!.
3. Сколькими нулями оканчивается число 16!?
Р е ш е н и е
В а р и а н т 1
1. Выбираем пять столов для школьников из 20 имеющихся (порядок выбора учитывается):
= 16 · 17 · 18 · 19 · 20 = 1 860 480.О т в е т: 1 860 480 способов.
2. п! = 7 (п – 1)!;
п (п – 1)! = 7 (п – 1)!;
п = 7.
О т в е т: п = 7.
3. В числе 12! содержится две пятерки и двойки, что дает два множителя 10. Значит, 12! заканчивается двумя нулями.
О т в е т: двумя нулями.
В а р и а н т 2
1. Выбираем семь стульчиков из 18 имеющихся (порядок выбора имеет значение):
= 12 · 13 · 14 · 15 · 16 · 17 · 18 = 160 392 960.О т в е т: 160 392 960 способов.
2. п! = 12 (п – 1)!;
п (п – 1)! = 12 (п – 1)!;
п = 12.
О т в е т: п = 12.
3. В числе 16! содержится три пятерки и двойки, что дает три множителя 10. Значит, 16! заканчивается тремя нулями.
О т в е т: тремя нулями.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется размещением из п элементов по k?
– Запишите формулу нахождения через факториалы.
– Запишите по комбинаторному правилу умножения.
Домашнее задание: № 835, № 836.
З а д а ч а. Из трехзначных чисел, записанных с помощью цифр 1; 2; 3; 4; 5; 6; 7; 8; 9 (без повторения цифр), сколько таких, в которых:
а) не встречаются цифры 6 и 7;
б) цифра 8 является последней?
У р о к 77 Дата:
СОЧЕТАНИЕ ИЗ п ЭЛЕМЕНТОВ ПО k (k ≤ п)
Цели: ввести понятие сочетания из п элементов по k (k ≤ п); вывести формулу нахождения числа сочетаний из п элементов по k; формировать умения решать комбинаторные задачи с применением данной формулы.
Ход урока
I. Организационный момент.
II. Устная работа.
1. З а д а ч а. В футбольном турнире участвуют несколько команд. Оказалось, что все они для трусов и футболок использовали белый, красный, синий, зеленый или желтый цвета, причем были представлены все возможные варианты.
а) Сколько команд участвовали в турнире?
б) Сколько команд играли в зеленых футболках?
в) У скольких команд футболки и трусы были разного цвета?
г) У скольких команд футболки и трусы были разного цвета, причем трусы были не красные?
2. Найти значение выражения:
а) Р4 + Р3; б) Р6 – Р5; в) ; г) ;
д) ; е) ; ж) ; з) .
III. Объяснение нового материала.
1. Объяснение нового материала целесообразно начать с решения практической задачи:
«Сколькими способами можно смешать по три краски из имеющихся пяти?».
Р е ш е н и е
Обозначим имеющиеся краски буквами латинского алфавита a, b, c, d, e. Выпишем возможные варианты смешивания красок, учитывая, что от порядка расположения красок результат не зависит:
abc, abd, abe, ace, ade
bcd, bce, bde
cde
Мы указали различные способы смешивания красок, в которых по-разному сочетаются три краски из данных пяти. Говорят, что мы составили все возможные сочетания из 5 элементов по 3.
2. Определение. Сочетанием из п элементов по k называют любое множество, составленное из k элементов, выбранных из данных п элементов.
П о д ч е р к и в а е м, что, в отличие от размещений, в сочетаниях не имеет значения
, в каком порядке указаны элементы. Два сочетания из п элементов по k отличаются друг от друга хотя бы одним элементом.
3. Обозначение. (читается «С из п по k»).
В рассмотренном примере мы нашли, что = 10.
4. Вывод формулы числа сочетаний из п по k, где k ≤ п.
В отличие от предыдущих тем, при доказательстве мы опираемся не напрямую на комбинаторное правило умножения, а на ранее выведенные формулы числа перестановок и размещений.
Сперва замечаем, что
(по комбинаторному правилу умножения), значит, 
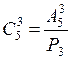.И затем проводим аналогичные рассуждения для общего случая:
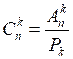
Учитывая, что
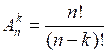, где п ≤ k, получаем, что  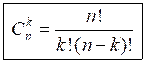| – формула вычисления числа сочетаний из п по k, где k ≤ п. |
5. Рассматриваем примеры задач на нахождение числа сочетаний из учебника на с. 184–185.
IV. Формирование умений и навыков.
Рассматриваем задачи на применение формулы нахождения числа сочетаний из п по k. Для предотвращения формального применения формулы требуем обоснования ее выбора.
Упражнения:
№ 768.
Р е ш е н и е
Выбираем 2 учащихся из 7, порядок выбора не имеет значения (оба выбранных пойдут на олимпиаду как полностью равноправные); количество способов выбора равно числу сочетаний из 7 по 2:
.О т в е т: 21 способ.
№ 770.
Р е ш е н и е
Выбор 6 из 10 без учета порядка:
.О т в е т: 210 способов.
№ 772.
Р е ш е н и е
Из 11 человек 5 должны поехать в командировку:
а) Заведующий едет, нужно выбрать еще 4 из 10 оставшихся:
