ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1044
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
б) Заведующий остается, нужно выбрать 5 из 10 сотрудников:
О т в е т: а) 210 способов; б) 252 способа.
Следующие три задачи – повышенной сложности.
№ 773.
Р е ш е н и е
а) Словарь выбирается, нужно выбрать еще 2 книги из 11:
б) Словарь не выбирается, выбираем 3 книги из 11:
О т в е т: а) 55 способов; б) 165 способов.
№ 774.
Эту задачу следует разобрать у доски. При решении используется не только формула числа сочетаний, но и комбинаторное правило умножения.
Р е ш е н и е
Сперва выбираем 4 маляров из 12:
Затем выбираем 2 плотников из 5:
Каждый из способов выбора маляров можно скомбинировать с каждым выбором плотников, следовательно, всего способов (по комбинаторному правилу умножения): 495 · 10 = 4950.
О т в е т: 4950 способов.
№ 775.
Р е ш е н и е
Нужно сделать два выбора: 3 книги из 10 ( способов) и 2 журнала из 4 ( способов) – порядок выбора значения не имеет. Каждый выбор книг может сочетаться с каждым выбором журналов, поэтому общее число способов выбора по правилу произведения равно:
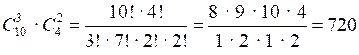
О т в е т: 720 способов.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется сочетанием из п элементов по k?
– Запишите формулу вычисления числа сочетаний из п элементов по k.
– В чем отличие сочетания из п элементов по k от размещения из п элементов по k.
Домашнее задание: № 769, № 771, № 783.
У р о к 78 Дата:
КОМБИНАТОРНЫЕ ЗАДАЧИ НА НАХОЖДЕНИЕ ЧИСЛА
ПЕРЕСТАНОВОК ИЗ пЭЛЕМЕНТОВ, СОЧЕТАНИЙ
И РАЗМЕЩЕНИЙ ИЗ пЭЛЕМЕНТОВ
по k (k ≤ п)
Цель: продолжить формирование умений находить число перестановок, сочетаний и размещений из п элементов по k.
Ход урока
I. Организационный урок.
II. Проверочная работа.
В а р и а н т 1
Найдите значение выражения:
а)
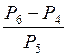 ; б)
; б) 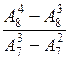 ; в)
; в) 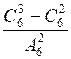 .
.В а р и а н т 2
а)
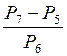 ; б)
; б) 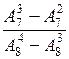 ; в)
; в) 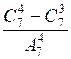 .
.Р е ш е н и е
В а р и а н т 1
а)
б)
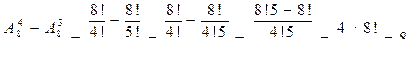 ;
;в)
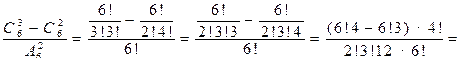
В а р и а н т 2
а)
б)
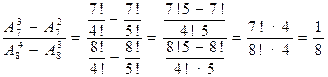 ;
;в)
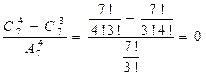 .
.III. Формирование умений и навыков.
1. В сильном классе можно предложить учащимся доказать два свойства сочетания из п элементов по k (п ≥ k) (или в качестве дополнительного задания интересующимся математикой учащимся):
:
П р и м е р: .
П р и м е р:
2. Следующие задачи решаются с применением формул нахождения числа перестановок, сочетаний и размещений.
№ 776. Р е ш е н и е
а) Фиксируем один элемент «в». Количество перестановок из пяти оставшихся элементов: Р5 = 5! = 1 · 2 · 3 · 4 · 5 = 120.
б) Фиксируем два элемента «а» и «т». Количество перестановок из 4 оставшихся элементов: Р4 = 4! = 1 · 2 · 3 · 4 = 24.
О т в е т: а) 120 анаграмм; б) 24 анаграммы.
№ 777. Р е ш е н и е
Мальчики и девочки должны чередоваться, то есть девочки могут сидеть только на четных местах, а мальчики только на нечетных. Поэтому девочки могут меняться местами только с девочками, а мальчики – только с мальчиками. Четырех девочек можно рассадить: Р4 = 4! = 24 способами, а пятерых мальчиков Р5 = 5! = 120 способами.
Каждый способ размещения девочек может сочетаться с каждым способом размещения мальчиков, поэтому по правилу произведения общее число способов равно: Р4 · Р5 = 24 · 120 = 2880.
О т в е т: 2880 способов.
№ 778 (а; в). Р е ш е н и е
Выбираем три элемента из 12, порядок выбора не имеет значения (все трое идут в наряд).
а) Иванов и Петров идут в наряд, еще одного нужно выбрать из других 10 солдат; количество способов выбора: = 10.
в) Иванов идет в наряд, а Петров остается. Еще двоих, идущих в наряд с Ивановым, нужно выбрать из других 10 солдат (Иванова и Петрова не считаем); количество способов:
О т в е т: а) 10 способов; в) 45 способов.
№ 779. Р е ш е н и е
а) Выбираем 4 шахматистов из 16 без указания порядка; количество способов:
б) Выбираем 4 шахматистов из 16 с указанием порядка их расположения в команде; количество способов:
О т в е т: а) 1820 способов; б) 43680 способов.
№ 780. Р е ш е н и е
Выбираем (без повторений) 2 буквы из 5 и 3 цифры из 10; порядок выбора учитывается (например: 213 кт и 321 тк – разные).
Количество способов выбора:
Каждый вариант выбора букв может сочетаться с каждым вариантом выбора цифр, поэтому, по комбинаторному правилу умножения, общее число способов равно:
О т в е т: 14400 способов.
№ 782. Р е ш е н и е
Выбираем из группы туристов в п человек четырех дежурных (порядок выбора значения не имеет); число способов . Затем выбираем из группы туристов в п человек двух дежурных – число способов . Так как число способов выбора четырех дежурных в 13 раз больше, чем двух, получаем уравнение:
= 13 · ;
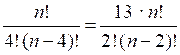 ;
;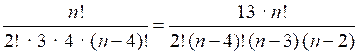 ;
;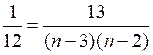 ;
;п2 – 5п – 150 = 0;
п1 = 15, п2 = –10. Так как п N, то п2 = –10 – не удовлетворяет условию, значит, п = 15.
О т в е т: 15 туристов.
IV. Итоги урока.
Ответить на контрольные вопросы на с. 187 учебника.
Домашнее задание: № 778 (б), № 781, № 844
У р о к 79 Дата:
ОТНОСИТЕЛЬНАЯ ЧАСТОТА СЛУЧАЙНОГО СОБЫТИЯ
Цели: ввести понятия случайного события, относительной частоты случайного события; формировать умение вычислять относительную частоту случайного события.
Ход урока
I. Организационный момент.
II. Устная работа.
Назовите комбинаторную формулу для решения задачи.
Учитель записывает на доске формулу, вычисления производить не надо.
1. Даны три лекарства А, В, С. Сколькими способами можно выписать назначение? (Р3 = 3!.)
2. Сколькими способами можно выбрать трех дежурных, если в классе 30 человек?
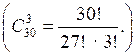
3. Сколько различных пятизначных чисел можно составить из цифр 5, 6, 7, 8, 9 при условии, что ни одна цифра в числе не повторяется? (Р5 = 5!.)
4. Сколько существует вариантов распределения трех призовых мест, если в предметной олимпиаде участвует семь человек?
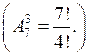
5. Даны четыре буквы А, В, С, Д. Сколько комбинаций по две буквы можно из них составить?
III. Объяснение нового материала.
Сперва необходимо создать у учащихся представление о «событии» и «случайном событии». Целесообразно опираться на личный опыт учащихся, поощрять их приводить примеры различных событий. Обращаем внимание на то, что есть обусловленные события, то есть наступающие тогда, когда выполнены некоторые условия. Например, увидев молнию, мы позже обязательно услышим гром. В других случаях в процессе наблюдения, опыта, эксперимента мы либо не знаем этих условий (обстоятельств), либо не умеем их учитывать, устранять. В этом случае речь идет о случайных событиях, которые могут произойти или не произойти.
Закономерности случайных событий изучает специальный раздел математики – теория вероятностей. Проводим небольшой экскурс в историю возникновения и развития этой науки.