ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1034
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1,05 · 10400 = 10920 р. – на счету через два года.
О т в е т: 10920 р.
4. № 876.
Р е ш е н и е
18, 18, 19, 20, 23, 24, 24, 25, 25, 25.
Среднее арифметическое:
= 22,1.Мода 25.
Медиана = 23,5.
Размах 25 – 18 = 7.
О т в е т: 22,1; 25; 23,5; 7.
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– В чем заключается основное свойство дроби?
– Правило изменения закона дроби.
– Правила сложения (вычитания) дробей с одинаковыми и разными знаменателями.
– Правила умножения и деления дробей.
– Правило нахождения процента от числа и числа по его проценту.
Домашнее задание: № 875 (а, в), № 878, № 879 (а).
У р о к 2 (86).
ЗНАЧЕНИЕ ВЫРАЖЕНИЯ, СОДЕРЖАЩЕГО СТЕПЕНЬ
И АРИФМЕТИЧЕСКИЙ КОРЕНЬ. ПРОГРЕССИИ
Цели: систематизировать знания учащихся по теме; обобщить умение нахождения значения выражения, содержащего степень и арифметический корень; повторить основные формулы для вычисления элементов прогрессий.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Вычислите:
а) 5–3; б)
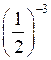; в) (–11)–2;г)
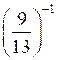; д)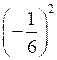 
; е) (–2)0.2. Вычислите:
а) ; б) ; в) ;
г)
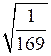; д) ; е) .III. Формирование умений и навыков.
1. Начинаем с актуализации знаний, повторяем свойства степени с целым показателем, определение и свойства арифметического квадратного корня.
Задания в форме теста:
а) Представьте выражение (х–2)3 · (х4)2 в виде степени с основанием х:
1) х; 2) х6; 3) х7; 4) х2.
б) Найдите значение выражения: (2,9 · 103) · (2 · 10–6):
1) 0,58; 2) 5800; 3) 0,0058; 4) 0,058.
в) Найдите частное от деления 4,8 · 107 на 1,6 · 104
:
1) 3; 2) 30; 3) 300; 4) 3000.
г) Упростите выражение:
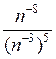:1) п–4; 2) п–23; 3) п7; 4) п10.
№ 887 (а).
Р е ш е н и е
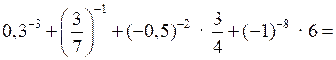
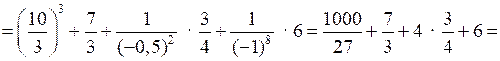
.О т в е т:
.№ 882 (а, г).
Р е ш е н и е
а)
.О т в е т: .
г)
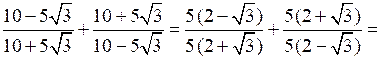
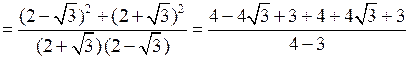= 14.О т в е т: 14.
№ 883.
Р е ш е н и е
.О т в е т: 73 – 36 .
№ 884 (а).
Р е ш е н и е
Преобразуем левую часть равенства.
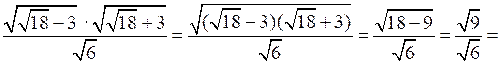
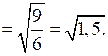
– верное равенство.№ 885 (а).
;
;
;
;
.
Так как
, то 
.Имеем: = – верное равенство.
2. Актуализация знаний по теме «Арифметическая и геометрическая прогрессии».
В о п р о с ы у ч а щ и м с я:
– Сформулируйте определение арифметической прогрессии. Приведите примеры числовой последовательности, которая является арифметической прогрессией.
– Запишите формулу п-го члена арифметической прогрессии.
– Запишите формулу суммы п первых членов арифметической прогрессии.
– Ответьте на аналогичные вопросы для геометрической прогрессии.
Упражнения:
№ 888.
Р е ш е н и е
(ап) – арифметическая прогрессия, а2 = –6, а3 = –2.
an = a1 + d (n – 1); d = a3 – a2; d = –2 – (–6) = 4;
a1 = a2 – d; a1 = –6 – 4= –10;
a15 = a1 + 14d; a15 = –10 + 14 · 4 = 46.
О т в е т: 46.
№ 889.
Р е ш е н и е
(хп) – арифметическая прогрессия; х2 = –2,4; d = 1,2.
Sn =
· n; х1 = х2 – d; х1 = –2,4 – 1,2 = –3,6;
;S10 = (2 · (–3,6) + 9 · 1,2) · 5 = (–7,2 + 10,8) · 5 = 18.
О т в е т: 18.
№ 890.
Р е ш е н и е
(bn) – геометрическая прогрессия,
.
;
;
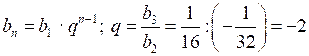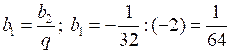.О т в е т: –32.
№ 891.
Р е ш е н и е
(хп) – геометрическая прогрессия, х2 = –32, ;
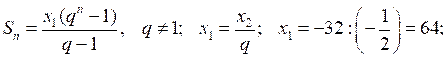
О т в е т: 42 .
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Сформулируйте свойства умножения и деления степеней с одинаковым основанием.
– Сформулируйте определение и свойства арифметического корня.
Домашнее задание: № 882 (б), № 884 (б), № 886, № 705 (а).
У р о к 3 (87).
ВЫЧИСЛЕНИЯ ПО ФОРМУЛАМ КОМБИНАТОРИКИ
И ТЕОРИИ ВЕРОЯТНОСТЕЙ
Цели: систематизировать знания учащихся по теме; обобщить умения применять формулы комбинаторики и теории вероятностей при решении задач.
Ход урока
I. Организационный момент.
II. Проверочная работа.
В а р и а н т 1
Найдите значение выражения:
1)
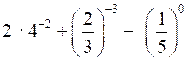;2)
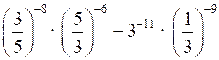;3)
;4)
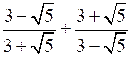.В а р и а н т 2
Найдите значение выражения:
1)
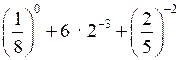;2)
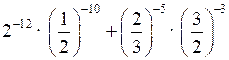;3)
;4)
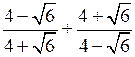.Р е ш е н и е
В а р и а н т 1
1)
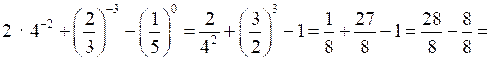
2)
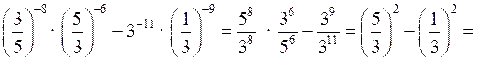
3)
.4)
