ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1035
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
В а р и а н т 2
1)
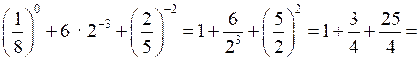
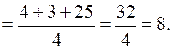
2)
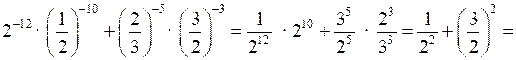
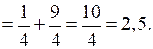
3)
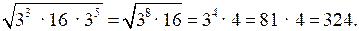
4)
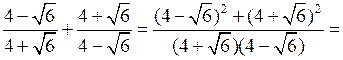
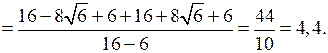
III. Формирование умений и навыков.
Актуализация знаний по теме «Элементы комбинаторики и теории вероятностей». Можно воспользоваться опорными конспектами, составленными на уроке обобщения темы.
№ 892 (а, д).
Р е ш е н и е
а)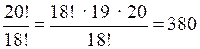
;
д)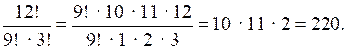
О т в е т: а) 380; д) 220.
№ 893 (б).
Р е ш е н и е
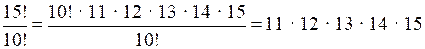
105 = 10 · 10 · 10 · 10 · 10.
Первое число представлено в виде произведения пяти положительных сомножителей, каждый из которых больше 10. Значит, > 105.
О т в е т: > 105.
№ 895.
Р е ш е н и е
Так как Алла дежурит в субботу, а Света в четверг, то остальные 4 школьника могут работать в любой из оставшихся четырех дней. Порядок имеет значение. Число комбинаций равно числу перестановок из 4 элементов: Р4 = 4! = 1 · 2 · 3 · 4 = 24.
О т в е т: 24 способа.
№ 896 (б).
Р е ш е н и е
В эстафете 4 100 м принимают участие четыре человека, по одному на каждом этапе. Так как тренеру важен порядок заплыва спортсменов, то число способов отбора спортсменов равно числу размещений из 12 элементов по 4:
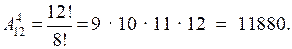
О т в е т: 11880 способов.
№ 897.
Р е ш е н и е
Число вариантов 3 научно-фантастических романов из 10 равно числу сочетаний из 10 по 3: (порядок выбора значения не имеет, так как Петя берет все три книги сразу, порядок прочтения не оговаривается). Аналогично число вариантов выбора 2 исторических романов из 8 равно . Так как каждый выбор научно-фантастических книг сочетается с каждым выбором исторических романов, то по комбинаторному правилу умножения общее число вариантов равно:
· =
.
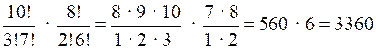О т в е т: 3360 способов.
№ 898.
Р е ш е н и е
Общее число билетов п = 150; извлечение каждого из них является равновозможным. Рассмотрим событие А – «полученный билет оказался выигрышным». Количество благоприятных исходов равно т = 30. Искомая вероятность:
.
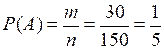Событие В – «полученный билет оказался невыигрышным». Количество благоприятных исходов т = 150 – 30 = 120.
.
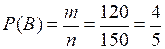П р и м е ч а н и е. Если в классе были пройдены понятия «противоположные события» и «вероятность противоположных событий», то можно заметить, что , тогда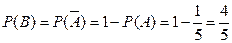
.
О т в е т: ; .
№ 900.
Р е ш е н и е
Число вариантов расстановки 5 фотоальбомов равно числу размещений из 5 элементов (порядок нам важен). Значит, общее число исходов равно п = Р5 = 5! = 1 · 2 · 3 · 4 · 5 = 120.
Событие А – «альбомы на полке оказались в том же порядке, что и прежде». Число благоприятных исходов т = 1 (только один вариант верный). Искомая вероятность:
.
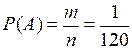О т в е т: .
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Назовите основные формулы комбинаторики.
– В чем отличие сочетаний из п элементов по k от размещений из п элементов по k?
– Назовите формулу вычисления вероятности случайного события при классическом подходе.
Домашнее задание: № 894; № 896 (а), № 899, № 901.
У р о к 4 (88).
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
РАЦИОНАЛЬНЫХ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ
Цели: систематизировать знания учащихся по теме; актуализировать умения и навыки приведения многочленов к стандартному виду, разложения многочлена на множители, использования формул сокращенного умножения, преобразования дробно-рациональных выражений.
Ход урока
I. Организационный момент.
II. Повторение учебного материала.
1. Правила раскрытия скобок, если перед ними стоит знак «плюс» («минус»).
2. Правило умножения одночлена на многочлен. Правило умножения многочлена на многочлен.
3. Формулы сокращенного умножения:
а) разность квадратов двух выражений;
б) квадрат суммы (разности) двух выражений;
в) сумма (разность) кубов двух выражений.
4. Что называют разложением многочлена на множители? Методы разложения многочлена на множители.
5. Действия над рациональными дробями.
III. Устная работа.
1. Преобразуйте в многочлен:
а) (5a – b) (5a + b); в) (2х + у)2;
б) (3a – 2b) (2b + 3a); г) (3х2 – 5у)2.
2. Вставьте вместо пропусков такие одночлены, чтобы полученное равенство было тождеством:
а) (15а – …)2 = … … + 144х2;
б) (… + 3ху)2 = … + 24ху + …;
в) (… – b2) (b2 + …) = 25 – b2;
г) (17 – …) (17 + …) = 289 – 9а2.
3. Укажите выражение, тождественно равное единице при условии, что х ≠ 3.
а) ; б) ; в) ; г) .
IV. Формирование умений и навыков.
№ 902 (а, в, д, ж).
Р е ш е н и е
а) (х – 2у) (х + 2у) + 4у2 = х2 – 4у2 + 4у2 = х2;
в) (5х – 1)2 + 10х = 25х2 – 10х + 1 + 10х = 25х2 + 1;
д)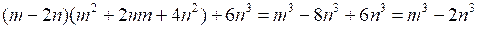
;
ж)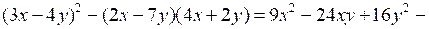
.
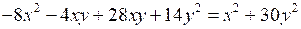О т в е т: а) х2; в) 25х2 + 1; д) т3 – 2п3; ж) х2 + 30у2.
№ 904 (а, в).
Р е ш е н и е
а) Преобразуем левую часть равенства:
;
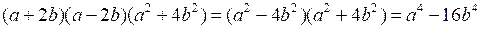a4 – 16b4 = a4 – 16b4 – верное равенство.
в) Преобразуем левую часть равенства:
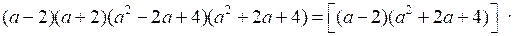
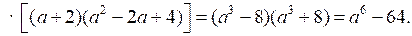
а6 – 64 = а6 – 64 – верное равенство.
№ 905 (а, в).
Р е ш е н и е
а) 12х3 – 3х2у – 18ху2 = 3х (4х2 – ху – 6у2);
в) 8ab – 14a – 12b + 21 = 4b(2a – 3) – 7(2a – 3) = (2a – 3)(4b – 7).
№ 906 (б, г, е).
Р е ш е н и е
б) 4b2 – 0,01c6 = (2b)2 – (0,1c3)2 = (2b – 0,1c3)(2b + 0,1c3).
г) х9 – 27 = (х3)3 – 33 = (х3 – 3)((х3)2 + 3 · х3 + 32) = (х3 – 3)(х6 + 3х3 + 9).
е) –20xy3 + 45x3y = 5xy(9x2 – 4y2) = 5xy((3x)2 – (2y)2) =
= 5xy(3x – 2y)(3x + 2y).
№ 907 (а, в).
Р е ш е н и е
а) Найдем корни квадратного трехчлена, решив уравнение:
х2 – х – 42 = 0. По теореме Виета, х1 · х2 = –42, х1 + х2 = 1.
Значит, х1 = 7; х2 = –6. По теореме о разложении квадратного трехчлена на множители:
х2 – х – 42 = (х – 7) (х + 6).
в) 81х2 + 18х + 1 = (9х)2 – 2 · 9 · х + 12 = (9х – 1)2.
П р и м е ч а н и е. При решении этих упражнений следует обращать внимание учащихся на методы разложения многочлена на множители:
– вынесение общего множителя (одночлена) за скобки;
– группировка и последующее вынесение общих множителей;
– разложение по формулам сокращенного умножения;
– разложение на множители квадратного трехчлена, имеющего корни.
При решении следующих упражнений используем:
а) Основное свойство алгебраической дроби – алгебраическую дробь можно сократить на ненулевой многочлен.
б) Арифметические действия над алгебраическими дробями:
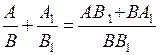
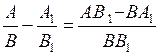
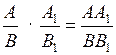
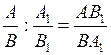
в) Свойства алгебраических дробей:
1) Если В
– ненулевой многочлен, то = 0.
2)
.
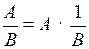3)
.
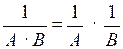№ 908 (г, д, и).
Р е ш е н и е
г)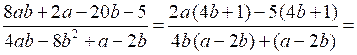
;
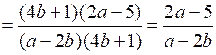д)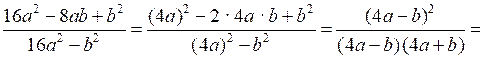
;
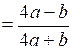и)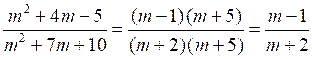
.
О т в е т: г)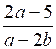
; д) 
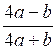; и) .
№ 910 (а, в).
Р е ш е н и е
а)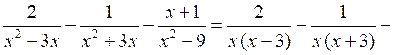
;
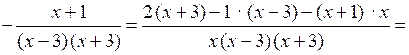
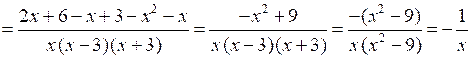в)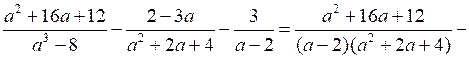
.
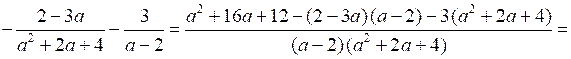
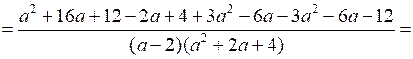
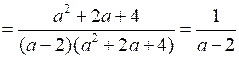О т в е т: а) ; в) .
В а р и а н т 2
1)
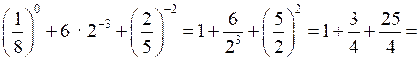
2)
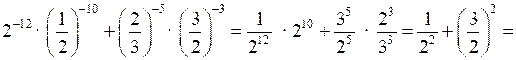
3)
4)
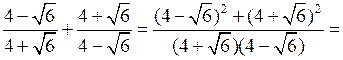
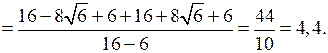
III. Формирование умений и навыков.
Актуализация знаний по теме «Элементы комбинаторики и теории вероятностей». Можно воспользоваться опорными конспектами, составленными на уроке обобщения темы.
№ 892 (а, д).
Р е ш е н и е
а)
;д)
О т в е т: а) 380; д) 220.
№ 893 (б).
Р е ш е н и е
105 = 10 · 10 · 10 · 10 · 10.
Первое число представлено в виде произведения пяти положительных сомножителей, каждый из которых больше 10. Значит, > 105.
О т в е т: > 105.
№ 895.
Р е ш е н и е
Так как Алла дежурит в субботу, а Света в четверг, то остальные 4 школьника могут работать в любой из оставшихся четырех дней. Порядок имеет значение. Число комбинаций равно числу перестановок из 4 элементов: Р4 = 4! = 1 · 2 · 3 · 4 = 24.
О т в е т: 24 способа.
№ 896 (б).
Р е ш е н и е
В эстафете 4 100 м принимают участие четыре человека, по одному на каждом этапе. Так как тренеру важен порядок заплыва спортсменов, то число способов отбора спортсменов равно числу размещений из 12 элементов по 4:
О т в е т: 11880 способов.
№ 897.
Р е ш е н и е
Число вариантов 3 научно-фантастических романов из 10 равно числу сочетаний из 10 по 3: (порядок выбора значения не имеет, так как Петя берет все три книги сразу, порядок прочтения не оговаривается). Аналогично число вариантов выбора 2 исторических романов из 8 равно . Так как каждый выбор научно-фантастических книг сочетается с каждым выбором исторических романов, то по комбинаторному правилу умножения общее число вариантов равно:
· =
.О т в е т: 3360 способов.
№ 898.
Р е ш е н и е
Общее число билетов п = 150; извлечение каждого из них является равновозможным. Рассмотрим событие А – «полученный билет оказался выигрышным». Количество благоприятных исходов равно т = 30. Искомая вероятность:
.Событие В – «полученный билет оказался невыигрышным». Количество благоприятных исходов т = 150 – 30 = 120.
.П р и м е ч а н и е. Если в классе были пройдены понятия «противоположные события» и «вероятность противоположных событий», то можно заметить, что , тогда
.О т в е т: ; .
№ 900.
Р е ш е н и е
Число вариантов расстановки 5 фотоальбомов равно числу размещений из 5 элементов (порядок нам важен). Значит, общее число исходов равно п = Р5 = 5! = 1 · 2 · 3 · 4 · 5 = 120.
Событие А – «альбомы на полке оказались в том же порядке, что и прежде». Число благоприятных исходов т = 1 (только один вариант верный). Искомая вероятность:
.О т в е т: .
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Назовите основные формулы комбинаторики.
– В чем отличие сочетаний из п элементов по k от размещений из п элементов по k?
– Назовите формулу вычисления вероятности случайного события при классическом подходе.
Домашнее задание: № 894; № 896 (а), № 899, № 901.
У р о к 4 (88).
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
РАЦИОНАЛЬНЫХ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ
Цели: систематизировать знания учащихся по теме; актуализировать умения и навыки приведения многочленов к стандартному виду, разложения многочлена на множители, использования формул сокращенного умножения, преобразования дробно-рациональных выражений.
Ход урока
I. Организационный момент.
II. Повторение учебного материала.
1. Правила раскрытия скобок, если перед ними стоит знак «плюс» («минус»).
2. Правило умножения одночлена на многочлен. Правило умножения многочлена на многочлен.
3. Формулы сокращенного умножения:
а) разность квадратов двух выражений;
б) квадрат суммы (разности) двух выражений;
в) сумма (разность) кубов двух выражений.
4. Что называют разложением многочлена на множители? Методы разложения многочлена на множители.
5. Действия над рациональными дробями.
III. Устная работа.
1. Преобразуйте в многочлен:
а) (5a – b) (5a + b); в) (2х + у)2;
б) (3a – 2b) (2b + 3a); г) (3х2 – 5у)2.
2. Вставьте вместо пропусков такие одночлены, чтобы полученное равенство было тождеством:
а) (15а – …)2 = … … + 144х2;
б) (… + 3ху)2 = … + 24ху + …;
в) (… – b2) (b2 + …) = 25 – b2;
г) (17 – …) (17 + …) = 289 – 9а2.
3. Укажите выражение, тождественно равное единице при условии, что х ≠ 3.
а) ; б) ; в) ; г) .
IV. Формирование умений и навыков.
№ 902 (а, в, д, ж).
Р е ш е н и е
а) (х – 2у) (х + 2у) + 4у2 = х2 – 4у2 + 4у2 = х2;
в) (5х – 1)2 + 10х = 25х2 – 10х + 1 + 10х = 25х2 + 1;
д)
;ж)
.О т в е т: а) х2; в) 25х2 + 1; д) т3 – 2п3; ж) х2 + 30у2.
№ 904 (а, в).
Р е ш е н и е
а) Преобразуем левую часть равенства:
;a4 – 16b4 = a4 – 16b4 – верное равенство.
в) Преобразуем левую часть равенства:
а6 – 64 = а6 – 64 – верное равенство.
№ 905 (а, в).
Р е ш е н и е
а) 12х3 – 3х2у – 18ху2 = 3х (4х2 – ху – 6у2);
в) 8ab – 14a – 12b + 21 = 4b(2a – 3) – 7(2a – 3) = (2a – 3)(4b – 7).
№ 906 (б, г, е).
Р е ш е н и е
б) 4b2 – 0,01c6 = (2b)2 – (0,1c3)2 = (2b – 0,1c3)(2b + 0,1c3).
г) х9 – 27 = (х3)3 – 33 = (х3 – 3)((х3)2 + 3 · х3 + 32) = (х3 – 3)(х6 + 3х3 + 9).
е) –20xy3 + 45x3y = 5xy(9x2 – 4y2) = 5xy((3x)2 – (2y)2) =
= 5xy(3x – 2y)(3x + 2y).
№ 907 (а, в).
Р е ш е н и е
а) Найдем корни квадратного трехчлена, решив уравнение:
х2 – х – 42 = 0. По теореме Виета, х1 · х2 = –42, х1 + х2 = 1.
Значит, х1 = 7; х2 = –6. По теореме о разложении квадратного трехчлена на множители:
х2 – х – 42 = (х – 7) (х + 6).
в) 81х2 + 18х + 1 = (9х)2 – 2 · 9 · х + 12 = (9х – 1)2.
П р и м е ч а н и е. При решении этих упражнений следует обращать внимание учащихся на методы разложения многочлена на множители:
– вынесение общего множителя (одночлена) за скобки;
– группировка и последующее вынесение общих множителей;
– разложение по формулам сокращенного умножения;
– разложение на множители квадратного трехчлена, имеющего корни.
При решении следующих упражнений используем:
а) Основное свойство алгебраической дроби – алгебраическую дробь можно сократить на ненулевой многочлен.
б) Арифметические действия над алгебраическими дробями:
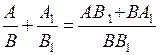
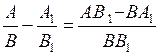
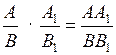
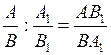
в) Свойства алгебраических дробей:
1) Если В
– ненулевой многочлен, то = 0.
2)
.3)
.№ 908 (г, д, и).
Р е ш е н и е
г)
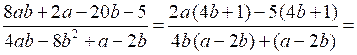
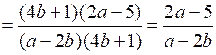;д)
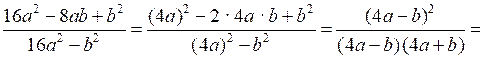
;и)
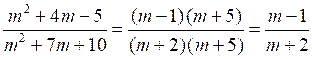.О т в е т: г)
; д) ; и) .№ 910 (а, в).
Р е ш е н и е
а)
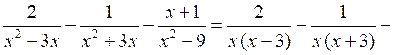
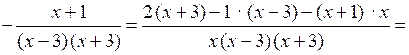
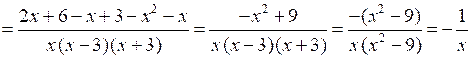;в)
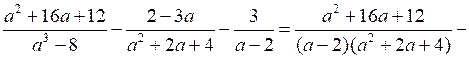
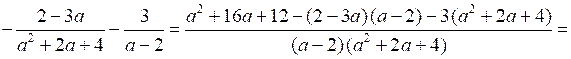
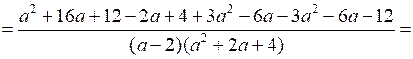
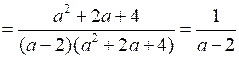.О т в е т: а) ; в) .