ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1032
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какие методы применяются для разложения многочленов на множители?
– Основное свойство алгебраической дроби?
– Что значит привести алгебраические дроби к общему знаменателю?
Домашнее задание: № 903 (а, в), № 905 (б, г), № 907 (б, г), № 910 (б, г).
У р о к 5 (89).
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
ДРОБНО-РАЦИОНАЛЬНЫХ
И ИРРАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ
Цели: систематизировать знания учащихся по теме; актуализировать умения и навыки упрощения и преобразования дробно-рациональных, иррациональных выражений и выражений со степенью.
Ход урока
I. Организационный момент.
II. Устная работа.
а) Какие из следующих выражений тождественно равно произведению (х – 2) (5 – х)?
1) (х + 2) (5 + х); 2) –(х + 2) (5 + х);
3) (х – 2) (х – 5); 4) (2 – х) (х – 5).
б) Упростите произведение:
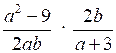.в) В каком случае выражение преобразовано в тождественно равное?
1) (2х – 5) у = 2х – 5у; 2) (х + у) (у – х) = х2 – у2;
3) (х – у)2 = х2 – у2; 4) (2 – х)2 = х2 – 4х + 4.
г) Разложите на множители многочлен х2 + 10х + 16.
д) Вычислите: ; ;
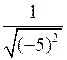.III. Формирование умений и навыков.
1. Продолжаем выполнение упражнений на преобразование алгебраических дробей.
№ 911 (б).
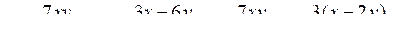
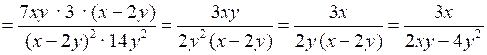.О т в е т:
.
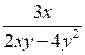
№ 912 (в).
Р е ш е н и е
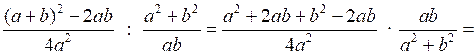
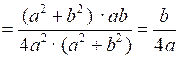.О т в е т: .
№ 914 (а, б).
Р е ш е н и е
а)
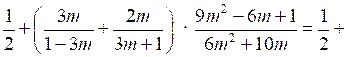
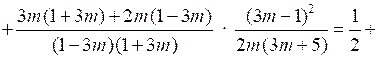
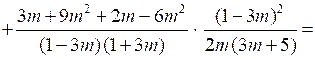
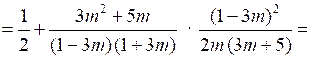
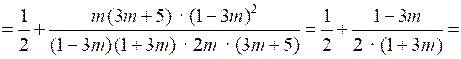
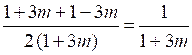.б)
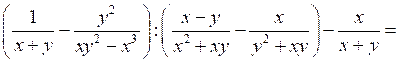
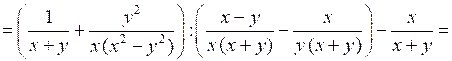
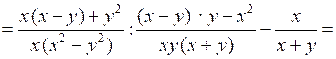
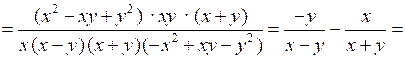
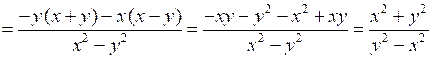.О т в е т: а) ; б)
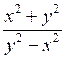.№ 915 (б).
Р е ш е н и е
. Возведем обе части равенства в квадрат.
; 
;;
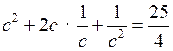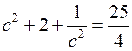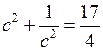; = 4,25.О т в е т: 4,25.
2. А к т у а л и з а ц и я з н а н и й – повторить определение арифметического корня и его основные свойства, методы освобождения от иррациональности в знаменателе дроби.
№ 919 (б, д, з). Устно.
№ 920 (а, в, д). Устно.
№ 921 (в).
Р е ш е н и е
О т в е т: .
№ 922 (б, е).
Р е ш е н и е
б)
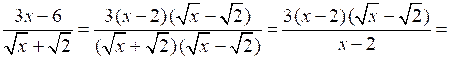
е)
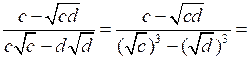
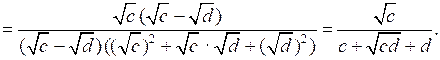
О т в е т: б)
; е) 
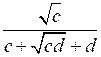.№ 924 (а).
Р е ш е н и е
;
;
;
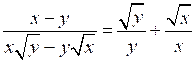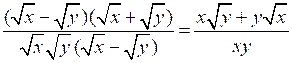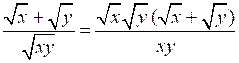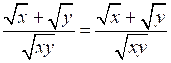– верное равенство.3. А к т у а л и з а ц и я з н а н и й – повторить свойства степени.
№ 917 (в).
Р е ш е н и е
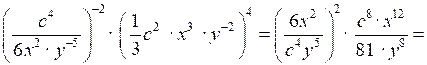
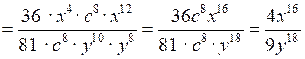.О т в е т:
.№ 918 (а).
Р е ш е н и е
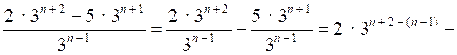
– 5 ∙ 3n + 1 – (n – 1) = 2 ∙ 33 – 5 ∙ 32 = 32(6 – 5) = 9.
О т в е т: 9.
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Назовите правила сложения, умножения и деления алгебраических дробей.
– Назовите определение арифметического корня и его свойства. Какие методы освобождения от иррациональности в знаменателе существуют?
– Сформулируйте определение и свойства степени с целым показателем.
Домашнее задание: № 913 (в, г), № 914 (г, д), № 918 (г), № 923 (в, г).
У р о к 6 (90).
ЛИНЕЙНЫЕ, КВАДРАТНЫЕ, БИКВАДРАТНЫЕ
И ДРОБНО-РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
Цели: систематизировать знания учащихся по теме; актуализировать умения и навыки решения уравнений с одной переменной перечисленных видов.
Ход урока
I. Организационный момент.
II. Проверочная работа.
В а р и а н т 1
1. Упростите выражение: 2у (у + 5) – 3у (у – 3).
2. Разложите на множители: 6тп – 3т2п + 3тп2.
3. Упростите выражение:
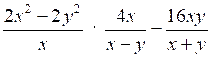.4. Вычислите: (103)2 · 10–8.
5. Упростите выражение:
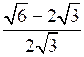.В а р и а н т 2
1. Упростите выражение: (а – 3) (а + 3) –2а (4 – а).
2. Разложите на множители: 4ас2 – 8ас + 4а2с.
3. Упростите выражение:
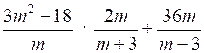.4. Вычислите: (213 · 2–11)–1.
5. Упростите выражение:
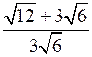.Р е ш е н и е
В а р и а н т 1
1. 2у(у + 5) – 3у(у – 3) = 2у2 + 10у – 3у2 + 9у = –у2 + 19у.
О т в е т: –у2 + 19у.
2. 6тп – 3т2п + 3тп2 = 3тп(2 – т + п) = 3тп (п – т + 2).
О т в е т: 3тп(п – т+ 2).
3.
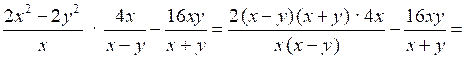
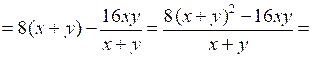
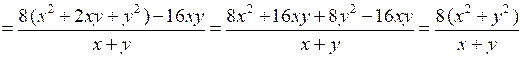.О т в е т:
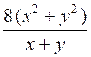.4. (103)2 · 10–8 = 106 · 10–8 = 106 – 8 = 10–2 = = 0,01.
О т в е т: 0,01.
5.
.
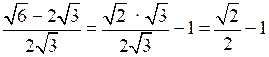
О т в е т: .
В а р и а н т 2
1. (а – 3) (а + 3) –2а (4 – а) = а2 – 9 – 8а + 2а2 = 3а2 – 8а – 9.
О т в е т: 3а2 – 8а – 9.
2. 4ас2 – 8ас + 4а2с = 4ас (с – 2 + а) = 4ас (а + с – 2).
О т в е т: 4ас (а + с – 2).
3.
.
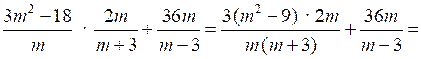
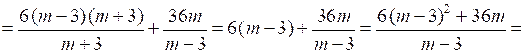
О т в е т:
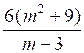.4. (213 · 2–11)–1 = (22)–1 = = = 0,25.
О т в е т: 0,25.
5.
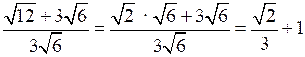.О т в е т: .
III. Повторение учебного материала.
А к т у а л и з а ц и я з н а н и й (определение и методы решения уравнений) по опорному конспекту или таблице (заранее заготовить).
| Вид уравнения | Методы решения |
| 1 | 2 |
| 1. Линейное ах = b, х – переменная, а, b – числа | 1) а ≠ 0, х = ; 2) а = 0, b ≠ 0, корней нет; 3) а = 0, b = 0, х – любое |
| 2. Квадратное ах2 + bх + с = 0, х – переменная, а, b, с– числа, а ≠ 0 | 1) с = 0, ах2 + bх = 0, х (ах + b) = 0, х = 0 или х = – |
| 2) b = 0, ах2 + с = 0; х2 = – ; – ≥ 0, x1, 2 = ; – < 0, корней нет | |
| 3) D = b2 – 4ac; D > 0, x1, 2 =  ;D = 0, x = – ; D < 0, корней нет | |
| 4) ax2 + 2kx + c = 0, D1 = k2 – ac, D1 > 0, x1, 2 =  ;D1 = 0, x = – ; D < 0, корней нет | |
| 5) x2 + px + q = 0, по теореме Виета, если х1, х2 – корни уравнения, то х1 + х2 = –р, х1 · х2 = q |