ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 1025
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3. № 475.
4. № 477.
Р е ш е н и е
Пусть первоначальный раствор содержал х г воды и у него была у %-ная концентрация.
Весь раствор имел массу (50 + х) г и в нем было у % соли. Получим уравнение:
(50 + х) · 0,01у = 50.
После добавления воды масса раствора будет (200 + х) г и у него станет (у – 7,5) %-ная концентрация. Соли в этом растворе останется 50 г. Получим уравнение:
(200 + х) · 0,01 (у – 7,5) = 50.
Составим систему уравнений:
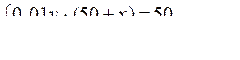
О т в е т: 200 г; 20 %.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какие существуют способы решения систем уравнений? Опишите их.
– Перечислите этапы решения задач на движение и задач на работу.
Домашнее задание: № 465, № 471, № 476
У р о к 51 Дата:
РЕШЕНИЕ ЛИНЕЙНЫХ НЕРАВЕНСТВ
С ДВУМЯ ПЕРЕМЕННЫМИ
Цели: ввести понятие неравенства с двумя переменными и его решения; формировать умение решать линейные неравенства с двумя переменными.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Какие из следующих чисел: –2; –1; 0; 2; 3 – являются решением неравенства х3 – 2х ≥ 1?
2. Подберите два каких-нибудь числа разных знаков, чтобы их сумма была больше 5.
III. Объяснение нового материала.
Объяснение нового материала проводить согласно пункту учебника. Сначала ввести понятие неравенства с двумя переменными и его решения, а затем разобрать, как решается линейное неравенство с двумя переменными.
Вопрос о решении неравенств второй степени с двумя переменными целесообразно рассмотреть на следующем уроке.
IV. Формирование умений и навыков.
1. № 482, № 483 (а, в).
2. № 484 (а, г), № 485.
3. Изобразите на координатной плоскости множество точек, задаваемое неравенством:
а) х < 2; в) –1 ≤ х ≤ 4;
б) у ≥ –3; г) –2 < у < 2.
4. № 492 (а).
Р е ш е н и е
ху ≥ 0.
Произведение двух чисел
является неотрицательным в том случае, если эти числа имеют одинаковые знаки. Значит, когда
Первой системе соответствует первая координатная четверть, а другой системе – третья координатная четверть.
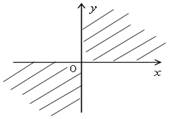
Сильным в учебе учащимся можно предложить дополнительно выполнить № 556.
Р е ш е н и е
| х | + | у | ≤ 1;
| у | ≤ 1 – | х |.
Построим график уравнения | у | = 1 – | х |. Для этого нужно раскрыть знаки модуля.
Получим четыре случая:
| 1) х ≥ 0, у ≥ 0; у = 1 – х. | 2) х ≥ 0, у < 0; –у = 1 – х; у = х – 1. |
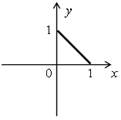 | 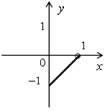 |
| 3) х < 0, у ≥ 0; у = 1 + x. | 4) x < 0, y < 0; –у = 1 + х; у = –х – 1. |
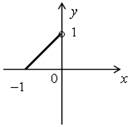 | 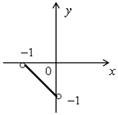 |
Объединяя все эти случаи, получим фигуру:
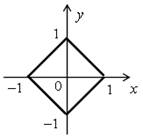
Данному неравенству удовлетворяет множество точек внутренней области этой фигуры.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется решением неравенства с двумя переменными?
– Сколько решений может иметь неравенство с двумя переменными?
– Как найти множество решений линейного неравенства с двумя переменными?
Домашнее задание: № 483 (б, г), № 484 (б, в), № 486.
У р о к 52 Дата:
РЕШЕНИЕ НЕРАВЕНСТВ ВТОРОЙ СТЕПЕНИ
С ДВУМЯ ПЕРЕМЕННЫМИ
Цель: формировать умение решать неравенства второй степени с двумя переменными.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Является ли пара чисел (–1; 2) решением неравенства:
а) 3х + 2у – 1 > 0;
б) 2х2 + 4у < 12;
в) х2 + у2 – 2х ≥ 7?
2. Найдите два каких-нибудь решения неравенства:
а) у ≥ х2 – 3;
б) х2 + у2 < 7.
III. Объяснение нового материала.
Разобрать примеры из учебника.
IV. Формирование умений и навыков.
Упражнения:
1. Изобразите на координатной плоскости множество решений неравенства:
а) у ≤ х2 + 2; г) ху < 8;
б) у > (х + 1)2 – 3; д) х2 + у2 ≥ 4;
в) ху ≥ 2; е) (х – 2)2 + (у + 1)2 < 16.
2. № 490 (а), № 491 (б).
3. № 489.
Р е ш е н и е
а) х2 + у2 – 6х – 4у + 13 ≤ 0.
Преобразуем выражение, стоящее в левой части неравенства, выделив в нем квадраты двучленов:
х2 – 6х + 9 – 9 + у2 – 4у + 4 – 4 + 13 ≤ 0;
(х – 3)2 + (у – 2)2 ≤ 0.
| Сумма квадратов двух выражений не может быть отрицательна. Поэтому данное неравенство выполняется только в том случае, если выражение (х – 3)2 + (у – 2)2 равно нулю, то есть при х = 3 и у = 2. Значит, данным неравенством задается всего одна точка с координатами (3; 2). | 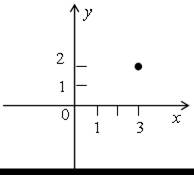 | |
| б) х2 – 4х – у + 5 ≥ 0; у ≤ х2 – 4х + 5; у ≤ х2 – 4х + 4 – 4 + 5; у ≤ (х – 2)2 + 1. Значит, данным неравенством задается множество точек, принадлежащих параболе у = (х – 2)2 + 1, и множество точек, расположенных ниже ее. | 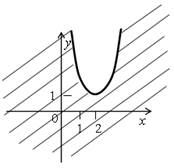 | |
| | | |
В классе с высоким уровнем подготовки можно дополнительно выполнить № 554.
Р е ш е н и е
| а) у ≥ | х | | | б) у ≤ | х – 2 | |
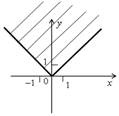 | | 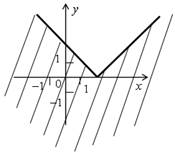 |
V. Итоги урока.
– Что называется решением неравенства с двумя переменными?
– Как решаются линейные неравенства с двумя переменными?
– Как задается неравенством множество точек координатной плоскости, расположенных:
а) выше (ниже) параболы у = 2х2 – 3х;
б) внутри окружности с центром в начале координат и радиусом 7?
Домашнее задание: № 487, № 488, № 490 (б), № 491 (а).
У р о к 53 Дата:
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ НЕРАВЕНСТВ
С ДВУМЯ ПЕРЕМЕННЫМИ
Цели: ввести понятие решения системы неравенств с двумя переменными; формировать умение решать системы линейных неравенств с двумя переменными.
Ход урока
I. Организационный момент.
II. Проверочная работа.
В а р и а н т 1
1. Изобразите на координатной плоскости множество решений неравенства:
а) у > 2х – 3; б) у ≤ (х + 2)2.
| 2. Задайте неравенством с двумя переменными множество точек заштрихованной области, изображенной на рисунке. | 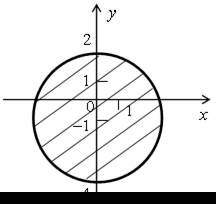 |