Файл: Учебнометодическое пособие для направлений подготовки 44. 03. 01 Педагогическое образование и 44. 03. 05 Педагогическое образование (с двумя профилями подготовки).docx

ЛАБОРАТОРНАЯ РАБОТА № 5

Определение ускорения поля тяготения Земли

методом оборотного маятника

Цель работы: ознакомление с одним из самых точных методов измерения ускорения свободного падения; определение ускорения поля тяготения Земли.

Принадлежности: оборотный маятник, механический или электронный секундомер.

Введение

Каждое тело, колеблющееся относительно оси, не проходящей через его центр масс, представляет собой физический маятник. Период колебания такого маятника определяется с достаточной степенью точности, выражением:

.

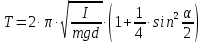Если угловая амплитуда физического маятника мала ( 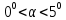), то в поле земного тяготения его период определяется:

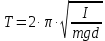. (1)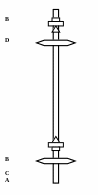

Из равенства (1) следует, что, если измерить период колебания маятника Т, его массу m, расстояние от оси подвеса до центра тяжести d, а также момент инерции I, то можно вычислить значение ускорения свободного падения g в любой точке. Однако для тел сколько-нибудь сложной формы вычисление или измерение величины момента инерции I достаточно трудная задача, которая не может быть решена с требуемой точностью.

Известно, что период математического маятника определяется:

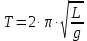. (2)

Можно и физический, и математический маятники привести в колебательное движение одновременно. Однако периоды их колебаний будут различны. Изменяя длину математического маятника, что очень легко сделать, можно подобрать ее такой, что периоды колебания и физического и математического маятника будут одинаковы. Тогда из сравнения равенств (1) и (2) следует:

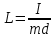. (3)

И эту величину (I/md) называют приведенной длиной физического маятника.

Можно показать, что если провести прямую, проходящую по нормали через ось подвеса и центр масс физического маятника, то на расстоянии L (L>md) найдется точка (центр качания), через которую можно провести вторую ось, и теперь заставив колебаться физический маятник относительно этой оси окажется, что периоды колебаний физического маятника (относительно точки подвеса и точки качания) будут равны.

---

Следовательно, если мы определим в маятнике положение двух осей, относительно которых маятник будет качаться с одним и тем же периодом, то расстояние между этими осями будет равно L – приведенной длине маятника. Измерив период и приведенную длину L мы можем, пользуясь формулой (2) найти ускорение силы тяжести g.

Для измерения ускорения силы тяжести g пользуются маятником особой конструкции, который носит название оборотного маятника (Рис. 1). Простейший оборотный маятник состоит из стержня 1, снабженного двумя чечевицами 2 и 3, а также двумя опорными призмами 4, на которые подвешивают маятник. В процессе измерения подбирают такое местоположение призм и чечевиц на стержне, при котором маятник, подвешенный поочередно на одной и на другой опорных призмах, колеблется с одинаковыми периодами.

Рассмотрим общий случай. Если расстояние между лезвиями призм L, а истинный период маятника, имеющего такую приведенную длину – T, то в действительности мы при наблюдении колебаний около обеих осей получим несколько различные периоды T₁ и T₂, которым будут соответствовать некоторые приведенные длины L₁ и L₂, отличающиеся от L. Напишем соответствующие соотношения:

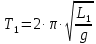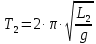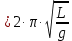, , T . (4)

Проделав несложные математические преобразования, получим:

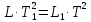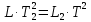, . (5)

Обозначим через a₁ и a₂ расстояния центра тяжести маятника до осей качания.

Используя теорему Штейнера, напишем для приведенных длин L₁ и L₂ следующие соотношения:

,

.

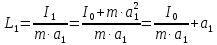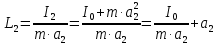Подставив данные выражения для L₁ и L₂ в равенства (5), получим:

,

---

.

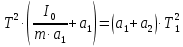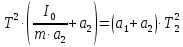
Решая данную систему уравнений относительно величины 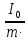, получим:

.

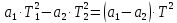Запишем вновь полученное уравнение в виде:

.

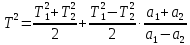Подставив данное выражение в равенство (2) и выполнив ряд несложных математических преобразований (не забывая, что 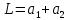), получим уравнение для ускорения свободного падения g:

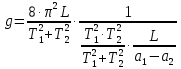. (6)

Это уравнение носит название уравнения Бесселя. Оно позволяет достаточно просто и с необходимой степенью точности найти величину ускорения свободного падения при приближенном равенстве периодов колебаний оборотного маятника.

Если T₁ и T₂ приближенно равны друг к другу, то уравнение (6) примет вид:

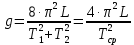. (7)

Описание установки и методики измерения. Оборотный маятник (как было отмечено ранее) представляет собой (смотри рис.) размеченный (цена деления 0,5 см) стержень 1, несущий на себе две жестко закрепленные призмы 4 и две чечевицы. Чечевица 2 (из металла) находится между призмами, чечевица 3 (из органического стекла) расположена ближе к концу стержня (за призмами). Чечевицы могут перемещаться по резьбе вдоль стержня при помощи чего и добиваются равенства периодов колебаний маятника.

Укрепив внешнюю чечевицу недалеко от конца маятника, а внутреннюю несколько ближе к противоположной призме, подвешивают маятник на упоре, расположенном ближе к внешней чечевице и определяют периоды колебаний оборотного маятника, устанавливая его последовательно на обе призмы.

Пусть периоды будут соответственно T₁ и T₂. Перемещением подвижных чечевиц (а при необходимости и призм) добиться совпадения периодов колебаний оборотного маятника на обоих призмах. При помощи секундомера определяют время t n=35-40 полных колебаний, а затем вычисляют время (период) 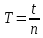одного полного колебания. (Внимание: отличие времени n=35-40 полных колебаний на каждой из призм, не должно превосходить 0,2 с.) (Примечание. При предварительных промерах периодов колебаний маятника, измерения можно вести приближенно, ограничиваясь

---

10-15 колебаниями, но по мере сближения периодов T₁ и T₂ следует увеличить число колебаний до n=35-40.)

Таким образом добившись совпадения периодов колебания на обоих призмах и зная приведенную длину L (расстояние между лезвиями призм), по формуле (7) рассчитать значения ускорения свободного падения g.

Для быстрого нахождения расположения подвижных чечевиц оборотного маятника, следует исходить из следующего соотношения: интервал перемещения выбранной одной чечевицы разбивают на три участка (A, B, C).

Проводят измерения периодов для этих положений T_1A, T_2A, T_1B, T_2B, T_1C, T_2C, если имеем, что (T_1A-T_2A)<0, (T_1B-T_2B)<0, (T_1C-T_2C)<0, то следует искать положение чечевицы удовлетворяющей равенству T₁₌T₂, в интервале BC. Его в свою очередь следует разбить на три интервала и провести аналогичный анализ.

Ограничиваясь расхождениями между T₁ и T₂ на 10^-3 с, рассчитать период как среднее значение. По формуле (7) рассчитать значения g в данной точке. L – приведенная длина оборотного маятника для случая (7) равна расстоянию между лезвиями призм. Её измеряют по рисками, нанесенным на стержень. Результаты занести в таблицу.

Сделать подробный вывод по проделанной работе.

n	t1, с	T1, с	t2, с	T2, с	Tср, с	L, м

Вопросы для допуска

1. 
   Дайте понятие пружинного, математического и физического маятника?
   
2. 
   Выведите период колебаний пружинного, математического и физического маятника?
   
3. 
   Дайте понятие момента инерции.
   
4. 
   Что такое приведенная длина физического маятника?
   
5. 
   Сравните метод измерения ускорения g с помощью оборотного маятника с методом измерения g математическим маятником.
   
6. 
   Почему угловая амплитуда колебаний не должна превышать 5⁰?
   
7. 
   Как зависит величина g от широты местности?
   
8. 
   Методика выполнения лабораторной работы.
   

---

Вопросы для защиты

Решение задачи на тему колебательного движения.

---