Файл: Учебное пособие для студентов очной и заочной форм обучения Рекомендовано учебнометодическим объединением вузов рф по образованию в области транспортных машин и транспортнотехнологических.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 30.10.2023

Просмотров: 198

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Рис. 1.1. Структурная схема шарнирно-рычажного механизма

поперечно-строгального станка

Пример 1

3.2. Определение сил и моментов сил инерции








В.С. Кутепов, А.А. Пашин, А.В. Плясов
СИСТЕМА «РИТМ» В КУРСЕ
ТЕОРИИ МЕХАНИЗМОВ И МАШИН




Федеральное агентство по образованию Российской Федерации



Тульский государственный университет


Кафедра Проектирование механизмов и деталей машин

В.С. Кутепов, А.А. Пашин,

А.В. Плясов
СИСТЕМА «РИТМ» В КУРСЕ

ТЕОРИИ МЕХАНИЗМОВ И МАШИН

(Вторая редакция)
Учебное пособие

для студентов очной и заочной форм обучения
Рекомендовано

учебно-методическим объединением вузов РФ по образованию

в области транспортных машин и транспортно-технологических

комплексов в качестве учебного пособия для студентов, обучающихся

по специальности 190206 «Сельскохозяйственные машины и оборудование»

ИЗДАТЕЛЬСТВО ТулГУ

Тула, 2009




УДК 534.1 + 538.56

Система «РИТМ» в курсе теории механизмов и машин. Учеб. пособие /В.С. Кутепов, А.А. Пашин, А.В. Плясов, Тул. гос. ун-т, Тула, 2009. – 50 с.
Излагаются краткие сведения по теории структурного, кинематического и динамического анализа механизмов и машин и даются примеры выполнения заданий по системе «РИТМ» с вопросами, которые используются в тестах по курсу и приведены соответствующие на них ответы.


Пособие предназначено для студентов высших учебных заведений дневной и заочной форм обучения по направлению 190200 – Транспортные машины и транспортно-технологические комплексы.

Печатается по решению библиотечно-издательского совета Тульского
государственного университета.


Рецензент: профессор, докт. тех. наук Матченко Н.М.


ISBN – 5 – 7679 – 0079- 5 © В.С. Кутепов, А.А. Пашин,

А.В. Плясов, 2009

© Тульский государственный

университет, 2009
Содержание

Стр.

Введение……………………………………………………………..…6

Содержание заданий …………………………………………………..6

1. Структурный анализ механизмов…………………………………..8

2. Кинематический анализ механизмов ………………………….....16

2.1. Задачи и методы…………………………………………...16

2.2. Свойства планов скоростей и ускорений…………….…..20

2.3. Примеры построения планов положений………………..20

2.4. Примеры построения планов скоростей…………………22

2.5. Примеры построения планов ускорений………………...28

3. Прикладная динамика машин…………...………………………...34

3.1. Силовой расчет механизма………………………………..34

3.2. Определение сил и моментов сил инерции………..……35

3.3. Величина и направление реакций…………….…..………36

3.4. Пример определения реакций в механизме……………...37

4. Анализ движения машинного агрегата…………………………...40

4.1. Динамическая модель машинного агрегата……………..40

4.2. Виды уравнений движения машинного агрегата……….41

4.3. Примеры построения динамических моделей…………..41

5. Контрольно-обучающие вопросы…………………………………44

5.1. Структура механизмов…………………………………….44

5.2. Кинематика механизмов…………………………………..46

5.3. Анализ движения машинного агрегата…………………..48

Рекомендуемый список литературы…………………………………50
Введение
Для приобретения умений и навыков решения задач анализа механизмов и машин и подготовки к выполнению курсового проектирования кафедра ПМДМ в третьем семестре параллельно с чтением лекций по курсу ТММ выдает студентам инженерных специальностей четыре задания по системе РИТМ.

Содержание заданий



Задание 1. Структурный анализ основного
шарнирно-рычажного механизма


    1. Начертить структурную схему механизма согласно заданию

    2. Определить число подвижных звеньев механизма. Назвать их и указать характер движения.

    3. Определить число кинематических пар. Указать их класс, вид и соединяемые ими звенья.

    4. Определить число степеней свободы механизма.

    5. Выделить структурные группы Ассура, определить число степеней свободы, класс и порядок каждой из них. Выделить начальное звено.

    6. Сделать вывод о структуре механизма и его классе.

    7. Определить число избыточных связей в механизме.

    8. Устранить избыточные связи или снизить их число понижением классов кинематических пар. Начертить структурную схему соответствующего механизма.

    9. Ответить на контрольно-обучающие тестовые вопросы.


Задание 2. Кинематический анализ основного механизма
2.1 Начертить кинематическую схему механизма, соответствующую заданному положению кривошипа.

    1. Записать векторные уравнения для построения плана скоростей.

    2. Построить план скоростей для заданного положения механизма.

    3. Определить величины и направления скоростей точек и угловых скоростей звеньев.

    4. Записать векторные уравнения для построения плана ускорений.

    5. Построить план ускорений для заданного положения механизма.

    6. Определить величины и направления ускорений точек и угловых ускорений звеньев.

    7. Ответить на контрольно-обучающие тестовые вопросы.

Задание 3. Силовой расчет механизма
3.1 Начертить наиболее удаленную от начального звена группу
Ассура.

    1. Вычислить для каждого звена главный вектор сил инерции и главный момент сил инерции.

    2. Приложить все действующие на звенья группы Ассура силы.

3.4 Составить уравнения статики для каждого звена группы Ассура.

3.5 Из уравнений статики аналитически и графически (построением замкнутого векторного многоугольника) определить неизвестные усилия.

3.6 Начертить промежуточную группу Ассура.

3.8 Далее последовательно, начиная с пункта 3.3, выполнить все операции для промежуточной группы Ассура.

3.9 Определить реакцию в кинематической паре, соединяющей начальное звено и стойку. Определить уравновешивающий момент (уравновешивающую силу).

3.10 Ответить на контрольно-обучающие тестовые вопросы.
Задание 4. Анализ движения машинного агрегата
4.1 Выбрать и изобразить динамическую модель механизма.

4.2 Записать выражение и определить численное значение
приведенного момента инерции .

4.3 Записать выражение и определить численное значение приведенного момента сил сопротивления .

4.4 Записать уравнения движения в интегральной и дифференциальной формах.

4.5 Ответить на контрольно-обучающие тестовые вопросы.
Задание РИТМ выполняется на листах белой бумаги формата А4 с одной стороны. Текст пишется карандашом (перовой или гелиевой ручкой с темными чернилами), разборчиво. Рисунки оформляются карандашом по линейке. Расчеты делаются с точностью до трех значащих цифр. Допускается (с разрешения преподавателя) выполнение заданий в школьной тетради (12 листов).

Приветствуется оформление задания на персональном компьютере.

Рассмотрим выполнение задания «РИТМ», разобрав в качестве примера схемы: поперечно-строгального станка, брикетировочного автомата и компрессора. Кроме схем механизмов в заданиях на РИТМ приводятся исходные данные: размеры звеньев, их массы, моменты инерции и усилия технологического сопротивления. Следует учитывать примечание, приведенное внизу таблицы в некоторых заданиях.

1. Структурный анализ механизма
Пример 1
1.1Структурной схемой называется схема, указывающая стойку, подвижные звенья, виды кинематических пар и их взаимное расположение. Структурная схема изображается по заданию. Например, схема поперечно-строгального станка (рис.1.1)

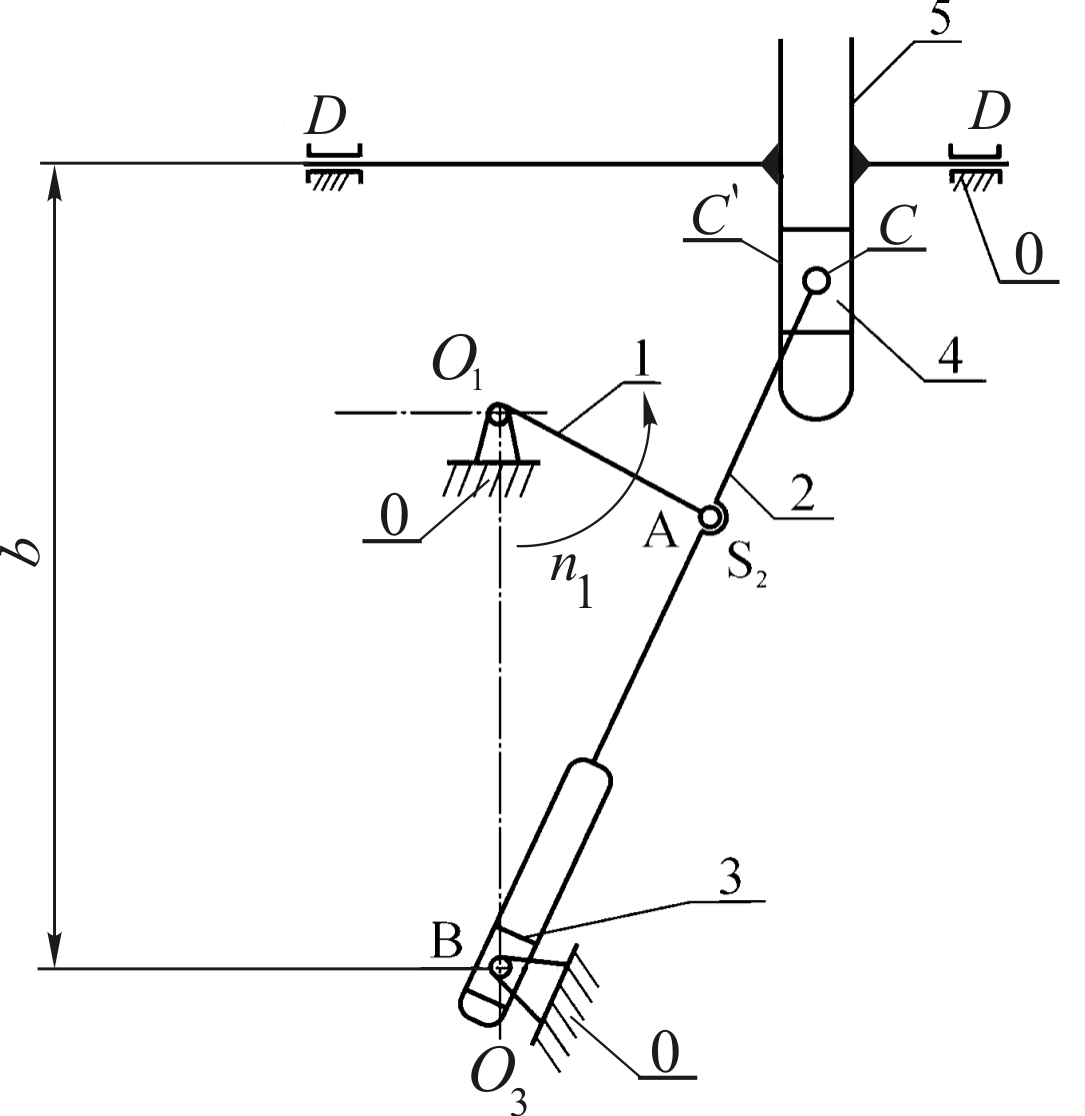
Рис. 1.1. Структурная схема шарнирно-рычажного механизма

поперечно-строгального станка



1.2 Звено– это деталь или несколько деталей, жестко связанных между собой и движущихся в механизме как одно целое.

Подвижные звенья обозначены на рис. 1.1 цифрами 1…5, неподвижное звено (стойка) цифрой 0. Подвижные звенья: 1 - кривошип, совершающий вращение вокруг точки О1 с постоянной частотой n1; 2 – кулиса, совершающая плоскопараллельное движение; 3 – камень, вращающийся вокруг точки О3; 4 – камень, движущийся поступательно; 5 – ползун, движущийся возвратно-поступательно. Входным звеном является кривошип 1, соединенный с приводом. Выходным звеном – ползун 5, с которым связан режущий инструмент поперечно-строгального станка. Механизм предназначен для преобразования вращательного движения кривошипа в возвратно-поступательное перемещение ползуна.

1.3 Кинематическая пара– это соединение двух соприкасающихся звеньев, допускающее их относительное движение. В данном механизме 7 кинематических пар. Все они являются низшими (их элементы – поверхности), высшие КП отсутствуют.

В данном механизме это кинематические пары:

Обозначение
О1
А
В
О3
С
С′
D

Соединяемые

звенья
0-1
1-2
2-3
3-0
2-4
4-5
5-0

Класс
5
5
5
5
5
5
5

Вид
Вращ.
Вращ.
Пост.
Вращ.
Вращ.
Пост.
Пост.


1.4 Число степеней свободы плоского механизма определим по формуле Чебышева



где – число подвижных звеньев,
– число низших кинематических пар, – число высших кинематических пар.

В нашем механизме =0, поэтому 3∙5 – 2∙7 = 1, то есть одна обобщенная координата определяет положение всех звеньев механизма. Следовательно, должно быть одно входное звено.

1.5 Любой механизм может быть образован путем последовательного присоединения к одному или нескольким начальным звеньям и стойке кинематических групп (групп Ассура) с нулевой сетью подвижности относительно тех звеньев, к которым группа присоединяется. Начальное звено – это звено, которому приписывается обобщенная координата. Это звено, образующее со стойкой кинематическую пару 5-го класса.








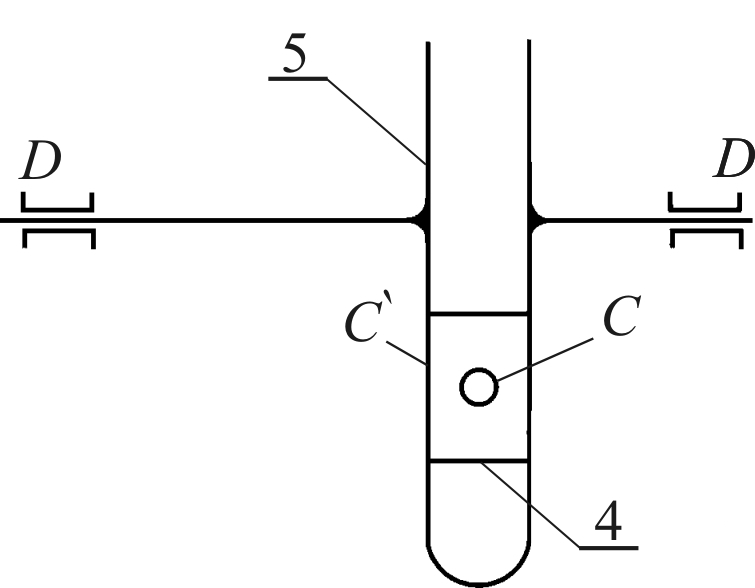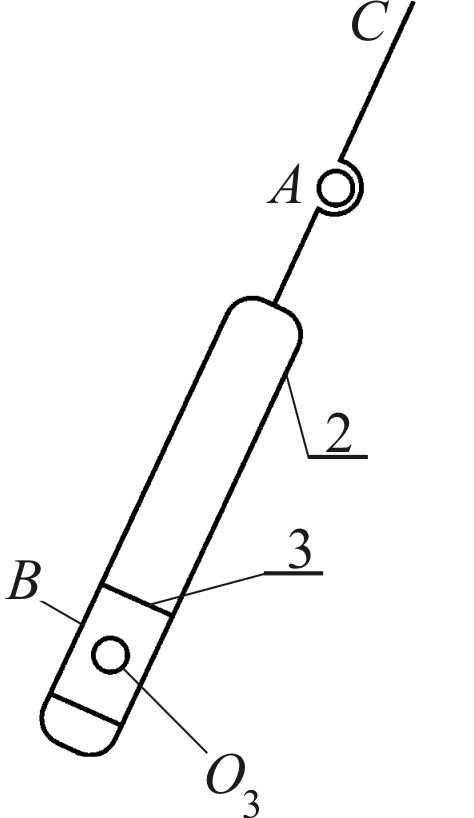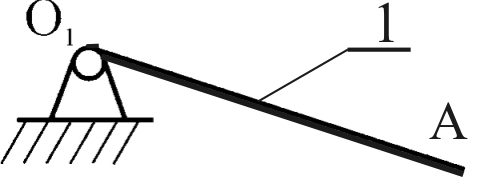Рис. 1.2. Группа 4-5

W= 3×2 – 2×3=0.

Класс 2-ой,

порядок 2-ой.
Рис. 1.3. Группа 2-3

W= 3×2 – 2×3=0.

Класс 2-ой,

порядок 2-ой.
Рис.1.4. Начальное звено

W= 3×1 – 2×1=1

Класс 1-ый,

порядок 1-ый

Структурная группа не изменяет числа степеней свободы механизма, к которому она присоединяется, то есть , откуда . Последнее условие выполняется, если = 2,4,6…, а …. Самая простая структурная группа состоит из двух звеньев и трех кинематических пар ( ). Это группа называется группой II класса, 2-го порядка. Порядок группы определяется числом свободных кинематических пар, которыми она может присоединяться к механизму.


Выделим группы Ассура согласно приведенному соотношению  и  , начиная с наиболее удаленных звеньев от начального звена. Изобразим группы Ассура и начальное звено.

1.6. Предложенный механизм является плоским шарнирно-рычажным механизмом, имеет одну степень свободы, состоит из двух структурных групп и начального звена. Класс механизма определяется наивысшим классом, входящих в него структурных групп. Рассматриваемый механизм – 2-го класса.

1.7. Число избыточных связей определяем по формуле , где =1…5, или для заданного механизма .

1.8. Устраним избыточные связи, понизив классы кинематических пар. Чтобы обеспечить , необходимо иметь для плоского механизма соотношение

0=1 – 6 +5 +4 +3 , откуда 6  – 1 = 5 +4 +3 . При =5 имеем
5 +4 +3
=29.

Вторым уравнением является условие неизменности числа кинематических пар: + + =7.

Первое равенство должно быть выполнено в механизме без избыточных связей, что обеспечивается =3, =2, =2 и 5×3 + 4×2 + 3 + 2 = 29 или  = 4,  = 0,  = 3 и 5×4 + 4×0 + 3×3 = 29. В обоих случаях число кинематических пар 3 + 2 + 2 = 7 и 4 + 3 = 7.

Более рациональным служит первое соотношение  = 3,  = 2,  = 2.

При понижении класса кинематических пар следует иметь в виду: как правило не понижается класс кинематических пар, образованных подвижными звеньями со стойкой ( , ) и поступательных пар.

Понизим класс кинематических пар. Схема соответствующего механизма показана на рис. 1.5.

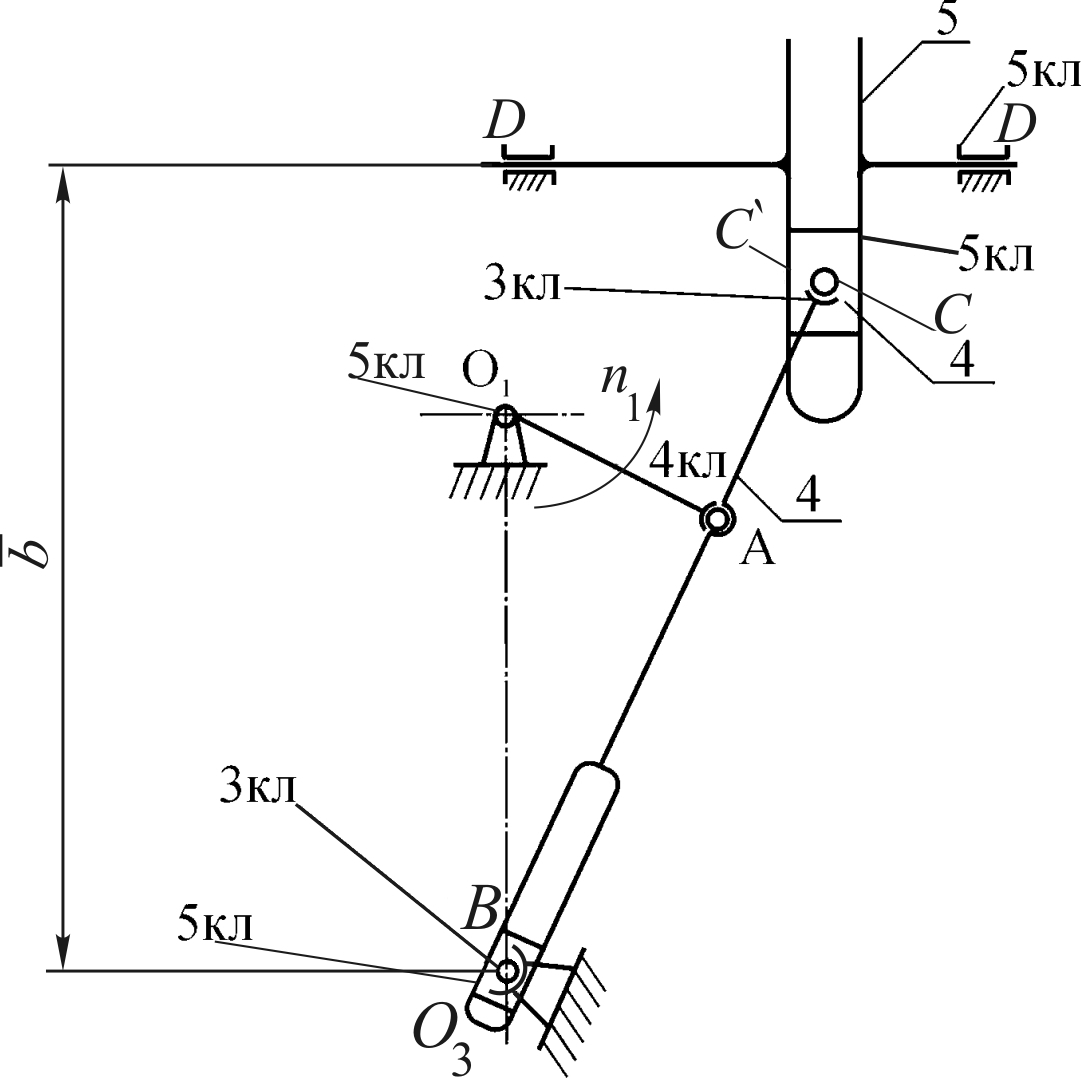
Примечание. Формальное устранение избыточных связей по уравнениям не всегда гарантирует их конструктивное исполнение. Так, невозможность применения пары 4-го класса в соединении звеньев 4-5 приводит к тому, что в контуре имеется лишняя степень свободы, тогда в контуре появляется одна избыточная связь.


Рис. 1.5. Схема механизма поперечно-строгального

Смотрите также файлы