Файл: Учебное пособие для студентов очной и заочной форм обучения Рекомендовано учебнометодическим объединением вузов рф по образованию в области транспортных машин и транспортнотехнологических.doc

и нагружают фиктивным моментом, мощность которого равна сумме мощностей, развиваемых всеми силами, действующими в механизме . Здесь обозначено: Jⁿ – момент инерции приведенной массы относительно оси вращения; Mⁿ – приведенный момент всех внешних сил;
М =М – М ; М – приведенный момент движущих сил, Нм; М – приведенный момент сил сопротивления; Нм.

4.2. Виды уравнений движения машинного агрегата

Уравнения движения модели зависят от типа машины, вида выполняемого ею технологического процесса, типа двигателя. Всего возможно 9 видов уравнений:





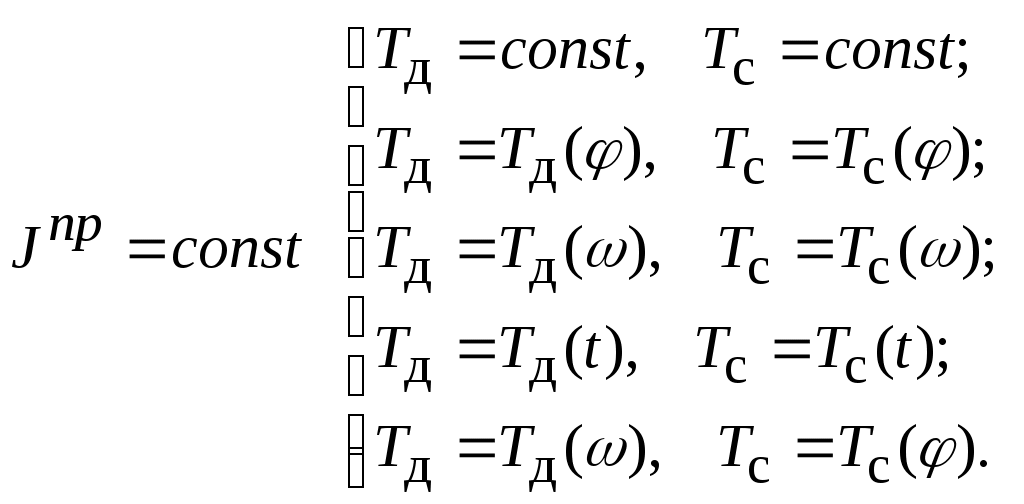
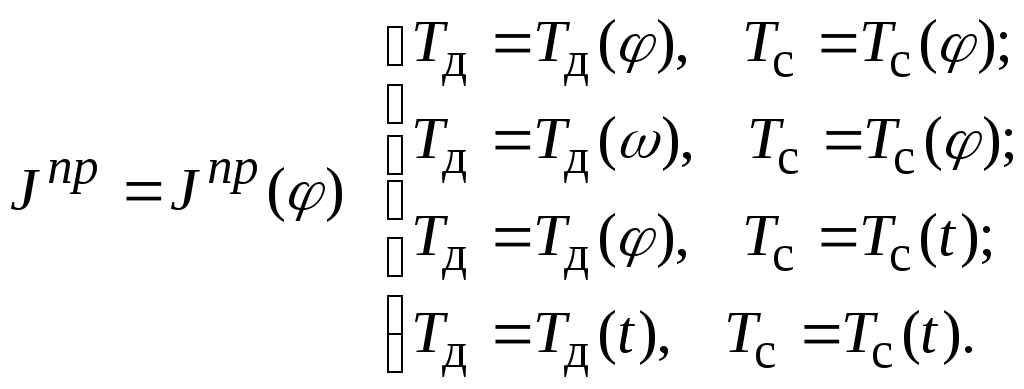
Пример 1 (рис. 2.5)
Найдем значения приведенных параметров Jⁿ и Mⁿ для данного положения механизма, полагая, что динамическая модель соответствует рис.4.1. Задано m₂, m₅, , , Р_р.

4.2. Запишем условие равенства кинетических энергий.

откуда



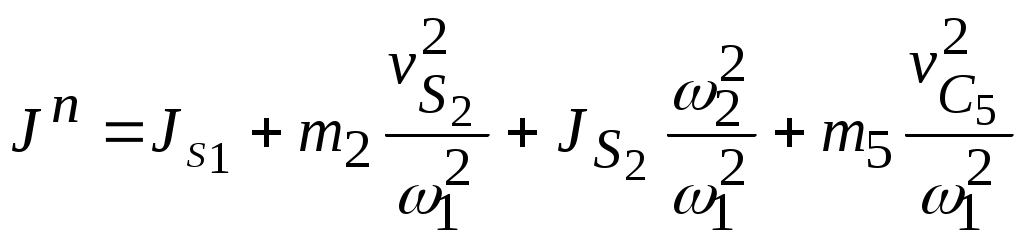
4.3. Для определения М запишем равенство мощностей

М

---

.

Для определения углов в последнем выражении прикладываем
вектора и в полюсе плана скоростей (рис. 2.6).

Поскольку ( )=₂=150, cos150= – 0,866, ( ) =90, , получаем формулу для вычисления приведенного
момента



4.4 Для одномассовой динамической модели уравнение движения в форме интеграла энергии запишем:

,

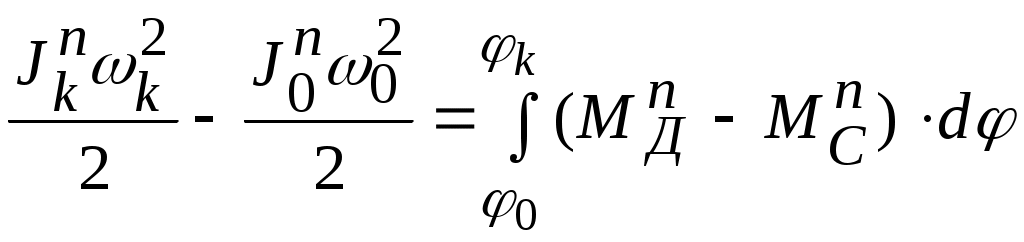где  – обобщенная координата, ₀ – приведенный момент инерции и угловая скорость звена приведения при = _0., – при угле .

В дифференциальной форме уравнение движения для динамической модели на рис. 4.1. запишем как:



или

,

где – угловое ускорение звена приведения (в нашем примере – кривошип).
Пример 2 (рис.2.7)
4.2. Задано: m₅, ,Р_р. Запишем равенство энергий:



или

.

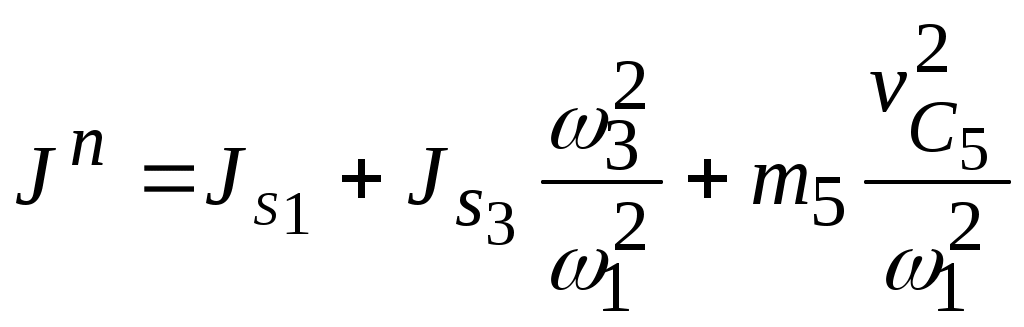4.3 Равенство мощностей:



Углы измеряем на плане скоростей (рис.2.8):

---

; .

Тогда = – P /₁

4.4 Этот пункт по выполнению аналогичен примеру 1.
Пример 3 (рис.2.10)
Задано: m₂, m₄, m₅, , .

Принимаем условно, что маховик с моментом инерции установлен на валу кривошипа.

4.2. Запишем равенство кинетических энергий:



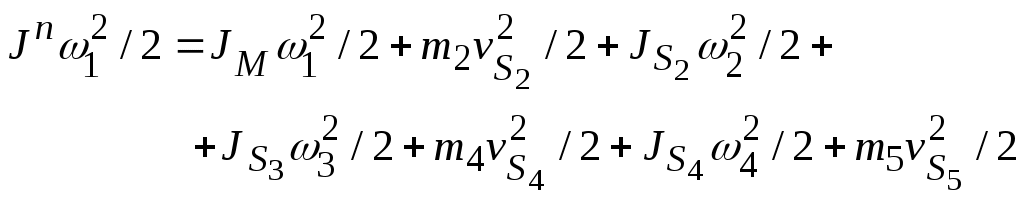
или



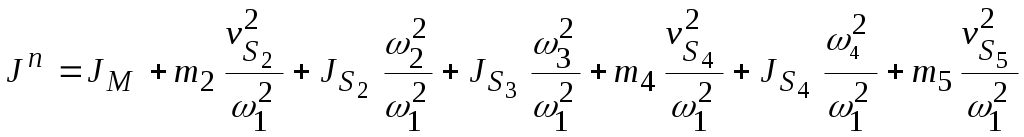
4.3. Равенство мощностей:



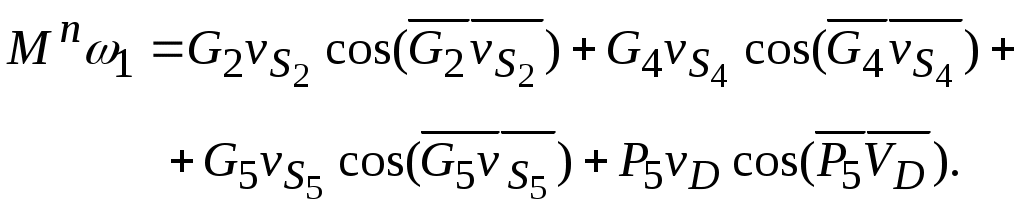
С учетом рис.2.10 и соответствующих значений углов ,

( )=180, ( )=180 имеем

.

---

4.4. Раздел аналогичен соответствующему разделу примера 1.

5. Контрольно-обучающие вопросы
5.1. Структура механизмов

1. Что такое звено?

2. Как называют неподвижное звено?

3. Как называют подвижное соединение звеньев?

4. Сколько неподвижных звеньев может входить в состав механизма?

5. Как называется звено, которому задается движение, преобразуемое механизмом в заданное движение других звеньев?

6. Как называется звено, совершающее движение, для осуществления которого предназначен механизм?

7. Укажите минимальное число промежуточных звеньев, необходимое для образования стержневого механизма.

8. Как называется звено стержневого механизма, которое входит во вращательную пару со стойкой и совершает полный оборот?

9. Как называется звено, образующее поступательную пару со стойкой?

10. Какое движение совершает кривошип?

11. Какое движение совершает коромысло?

12. Какое движение совершает шатун?

13. Какое движение совершает ползун?

14. Какое замыкание элементов кинематической пары (КП) может использоваться при соединении звеньев?

15. Какое замыкание реализуется в сферической КП?

16. Какое замыкание реализуется во вращательной КП?

17. Какие КП входят в состав стержневого механизма?

18. Чему равна степень подвижности структурной группы Ассура?

19. В каких границах находится класс КП?

20. Укажите класс вращательной КП.

21. Укажите класс поступательной КП.

22. Укажите класс винтовой КП.

23. Укажите класс КП «шар-плоскость».

24. Что называется числом степеней свободы механизма?

25. По какой формуле рассчитывается степень подвижности плоского механизма?

26. По какой формуле рассчитывается степень подвижности пространственного механизма?

27. Что необходимо сделать для устранения избыточных связей?

28. Будет ли механизм с избыточными связями неработоспособным?

29. Какие механизмов различают по виду используемых КП?

30. Что такое элементы КП?

31. Какие элементы имеют высшие КП?

32. Какие элементы имеют низшие КП?

33. Какие элементы КП в кинематической паре 3-его класса?

34. Соединяет ли КП подвижное звено со стойкой?

35. Назначение КП.

36. Какие КП более надежные – высшие или низшие?

37. В каких КП – высших или низших – потери на трение меньше?

38. В каких КП (высших или низших) наименьший износ соприкасающихся поверхностей?

39. Какие КП используются в точных ненагруженных механизмах?

---

40. Какие КП рекомендуется применять при передаче значительных усилий?

41. Что называется кинематической цепью (КЦ)?

42. Виды КЦ.

43. Что такое механизм?

44. Каков класс механизма шарнирного четырехзвенника?

45. Как определяется порядок группы Ассура?

46. Как определить класс группы Ассура?

47. Как определить класс механизма?

48. Как устранить избыточные связи в механизме?

49. Принцип образования плоских замкнутых механизмов по Ассуру.

50. Какой класс имеет начальное звено?
Ответы

1. Деталь или группа деталей, жестко связанные между собой.
2. Стойка. 3. Кинематическая пара. 4. Одно.
5.Входное. 6.Выходное. 7. Одно. 8. Кривошип. 9. Ползун. 10. Вращательное. 11. Возвратно-вращательное (колебательное). 12. Плоскопараллельное. 13. Возвратно-поступательное. 14. Силовое, геометрическое.
15. Геометрическое. 16. Геометрическое. 17. Низшие 18. Нулю. 19. 1…5.
20. 5-ый. 21. 5-ый. 22. 5-ый. 23. 1-ый. 24. Число обобщенных координат.
25. W_П = 3n – 2р_Н - р_В. 26. W = 6n – 5р₅ - 4р₄ - 3р₃ - 2р₂ - р₁.
27. Понизить класс КП. 28.Да. 29. С низшими и высшими КП.
30. Поверхности, линии и точки, по которым происходит соприкосновение звеньев, входящих в КП. 31.Линии, точки. 32.Поверхности.33.Поверхности.
34. Да. 35. Подвижное соединение звеньев. 36. Низшие. 37. В высших.
38. В низших. 39. Высшие. 40. Низшие. 41. Система звеньев, связанная посредством КП. 42. Пространственные и плоские, простые и сложные, замкнутые и незамкнутые. 43.Кинематическая цепь с неподвижным звеном,
число степеней которой равно числу обобщенных координат, характеризующих положение цепи относительно стойки. 44. 2-ой.
45. Количеством КП, с помощью которых она присоединяется в механизме.
46. Определяется числом КП, заключенных в простейшем замкнутом контуре групп Ассура. 47. По наивысшему классу группы Ассура. 48. Понизить класс КП. 49. Путем присоединением к начальному звену и стойке групп звеньев с нулевой степенью подвижности. 50. Первый.

5.2. Кинематика механизмов
1. Как вычисляется масштабный коэффициент плана положений схемы механизма?

2. С какой точки механизма начинается построение планов скоростей и ускорений?

3. Что такое план скоростей для конкретного положения механизма?

---