Файл: Учебное пособие для студентов очной и заочной форм обучения Рекомендовано учебнометодическим объединением вузов рф по образованию в области транспортных машин и транспортнотехнологических.doc

станка без избыточных связей
Пример 2
1.1. Рассмотрим схему кулисного механизма брикетировочного автомата. Изобразим структурную схему (рис.1.6).

1.2. Подвижные звенья: 1 – кривошип (вращение вокруг точки ); 2 – камень (плоскопараллельное движение); 3 – кулиса (возвратно - вращательное движение); шатун (плоскопараллельное движение); 5 – ползун (возвратно-поступательное движение).

Подвижных звеньев  = 5.

Входное звено 1 – кривошип, выходное – ползун 5.

1.3 Кинематические пары.

Обозначение	О1	A	B	О3	C	D	D΄
Соединение звеньев	0-1	1-2	2-3	3-0	3-4	4-5	5-0
Класс	5	5	5	5	5	5	5
Вид	Вращ.	Вращ.	Пост.	Вращ.	Вращ.	Вращ.	Пост.

Всего кинематических пар 7, все низшие.

1.4.

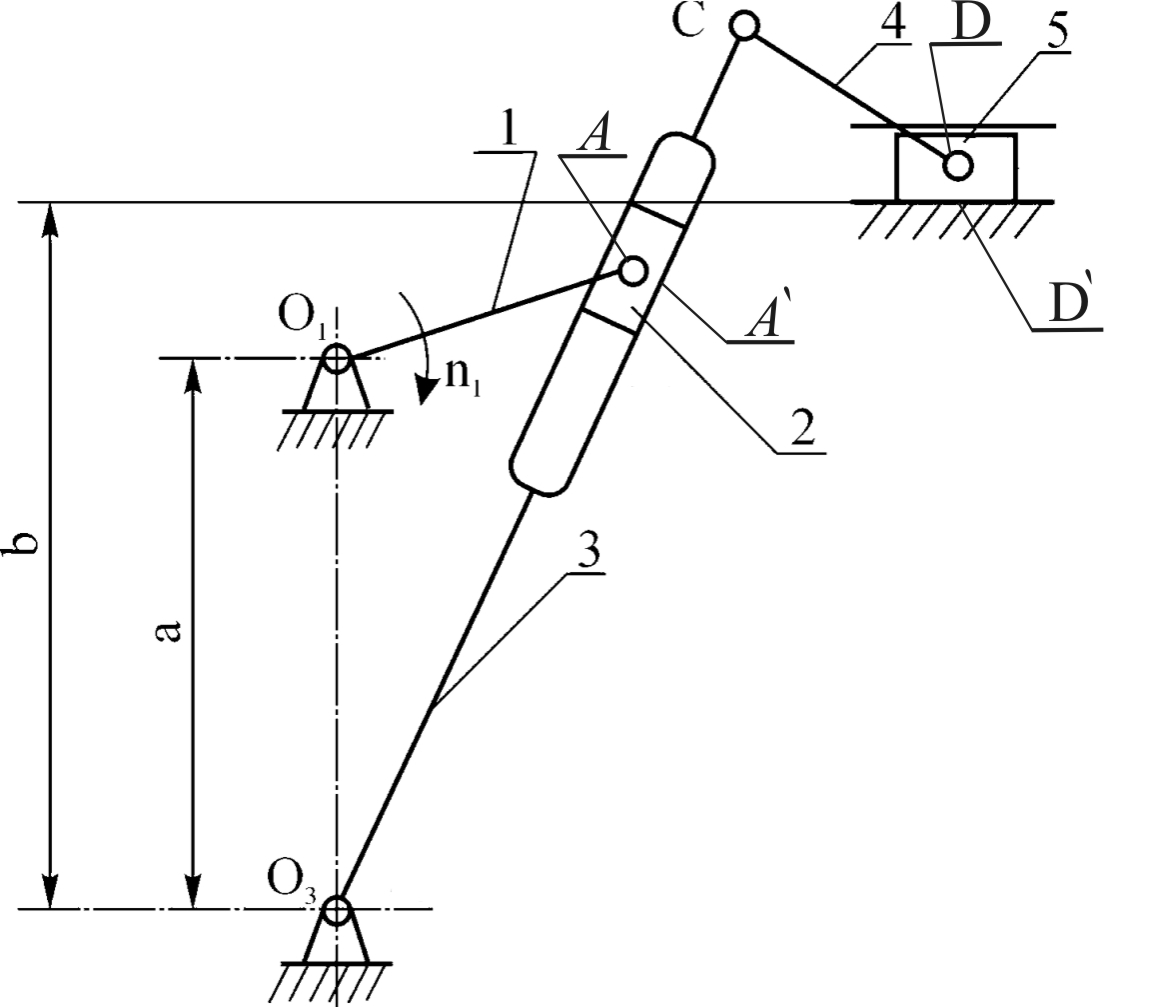
Рис. 1.6. Структурная схема механизма брикетировочного автомата

1.5. Группы Ассура и начальное звено.

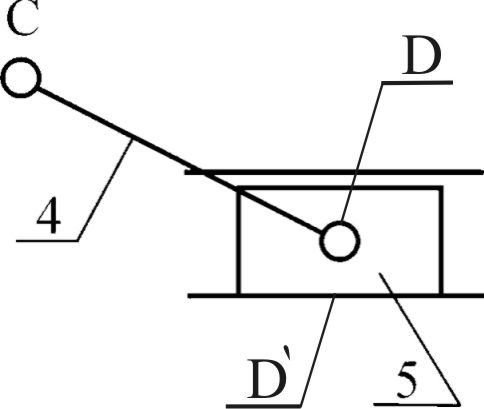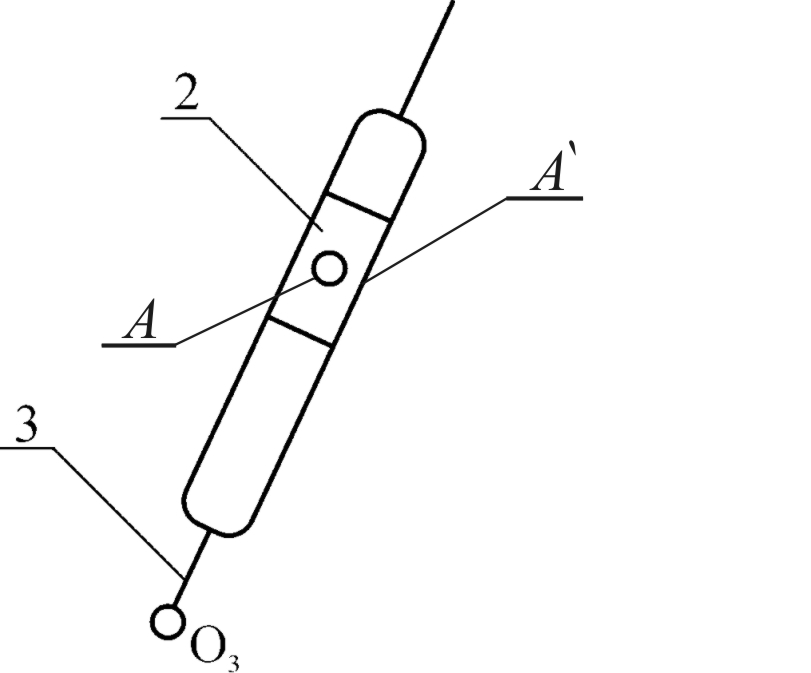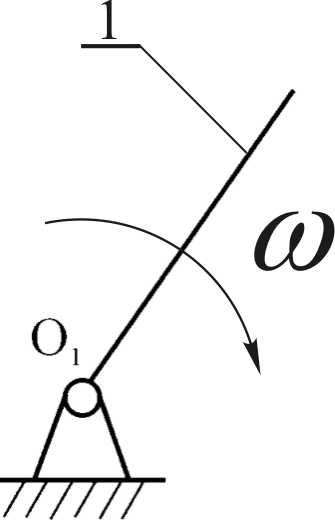Рис. 1.7. Группа 4-5 W=3 –2 =3×2–2×3=0. Класс 2-ой, порядок – 2-ой.	Рис. 1.8. Группа 2-3 W=3 –2 =3×2–2×3=0. Класс 2-ой, порядок – 2-ой.	Рис.1.9 Начальное звено W=3 -2 =3×2-2×1=1 Класс 1-ый, порядок 1-ый.

---

1.6. Механизм шарнирно-рычажный, плоский, 2-го класса. Имеет одну степень свободы. Состоит из двух структурных групп и начального звена.

1.7. Избыточные связи: , где =1…5, или для
заданного механизма .

Принимаем соотношение 5 +4 +3 =29, получаемое при =3, =2, =3.

1.8. Понижаем класс кинематических пар соединений звеньев 0-3, 4-5 до 3-его; 1-2, 2-4 до 4-го. Схема механизма при =0 показана на
рис. 1.10.



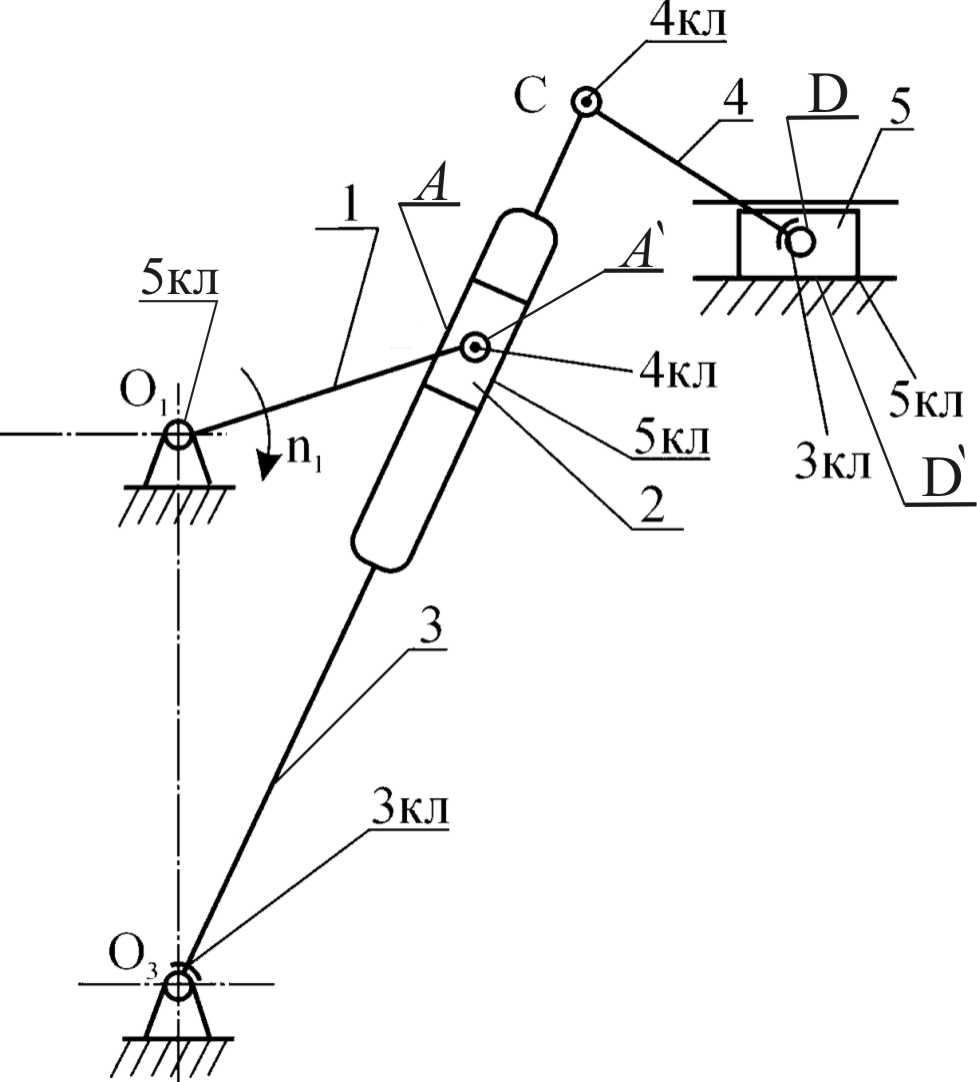
Рис. 1.10. Схема механизма брикетирования без избыточных связей

Пример 3
1.1 Схема механизма компрессора (рис.1.11).

1.2. Подвижные звенья:

1 – кривошип (вращение вокруг точки О₁); 2 – шатун (плоскопараллельное движение); 3 – коромысло (возвратно-вращательное движение); 4 – шатун (плоскопараллельное движение); 5 – ползун (возвратно-поступательное движение).

Подвижных звеньев n = 5.

Входное звено 1 – кривошип, выходное – ползун 5.

Механизм предназначен для преобразования вращательного
движения кривошипа в возвратно-поступательное движение ползуна.

1.3. Кинематические пары.

Обозначение	О1	A	B	О3	C	D	D΄
Соединение звеньев	0-1	1-2	2-3	3-0	3-4	4-5	5-0
Класс	5	5	5	5	5	5	5
Вид	Вращ.	Вращ.	Вращ.	Вращ.	Вращ.	Вращ.	Пост.

---

Всего кинематических пар 7, все низшие.

1.4. , Тогда W = 1.

В механизме одно ведущее звено (кривошип 1).


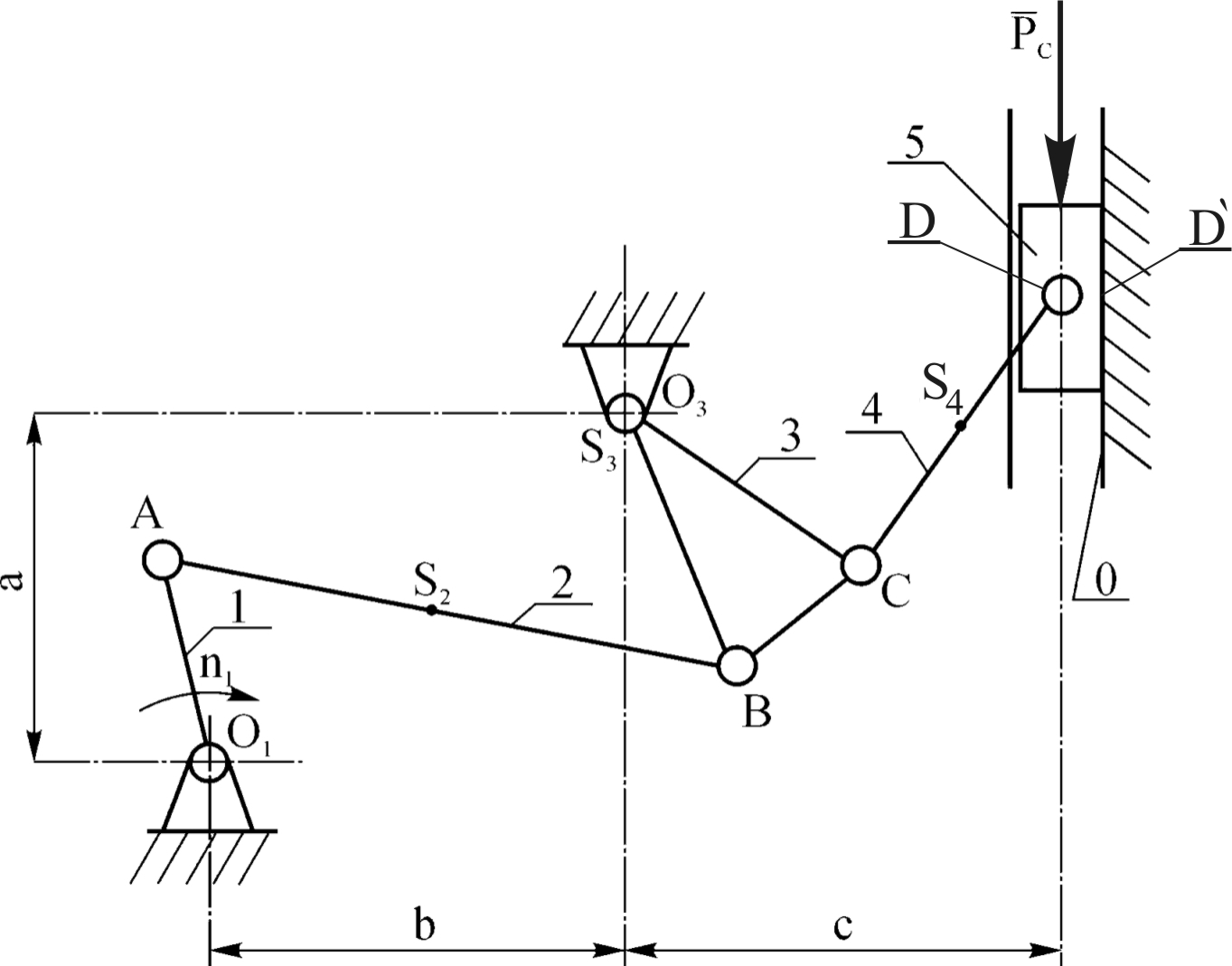
Рис. 1.11. Структурная схема механизма компрессора
1.5. Группы Асура и начальное звено.

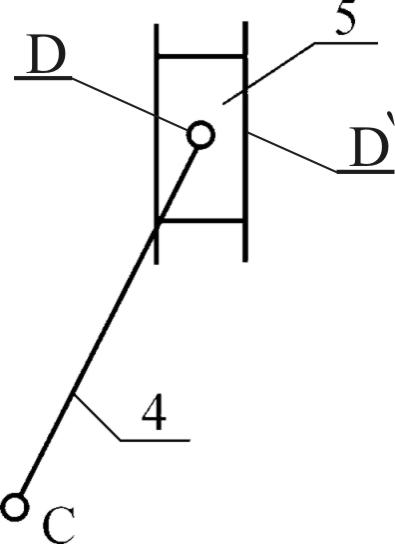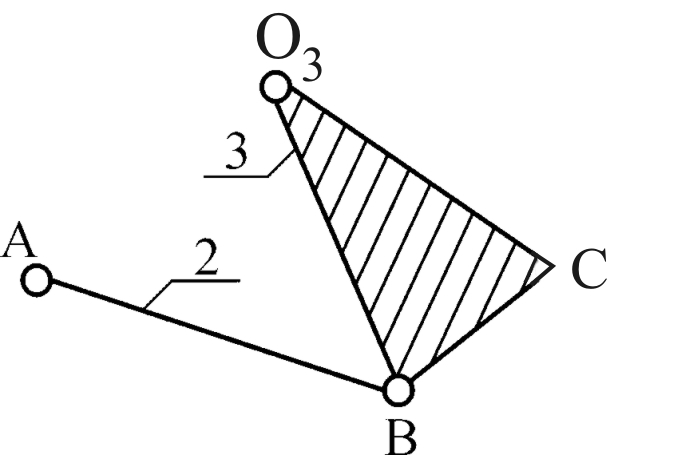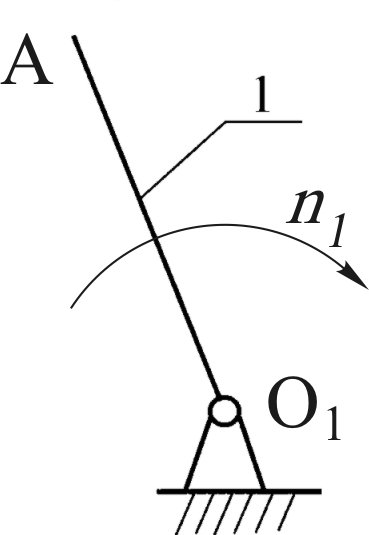Рис. 1.12. Группа 4-5 Класс 2-ой, порядок – 2-ой.	Рис. 1.13. Группа 2-3 Класс 2-ой, порядок – 2-ой.	Рис. 1.14 Начальное звено Класс 1-ый, порядок 1-ый

5. 
   Механизм шарнирно-рычажный, плоский, 2-го класса.
   
6. 
   Избыточные связи q= W-6n+5p₅=1-65+57=6.
   
7. 
   Принимаем соотношение 5р₅+4р₄+3р₃=29, получаемое при р₅=3, р₄=2, р₃=2. Понижаем класс кинематических пар, например, соединений звеньев 4-5, 2-3 до 3-его, 1-2, 3-4 – до 4-го. Получаем схему механизма (рис. 1.15).
   

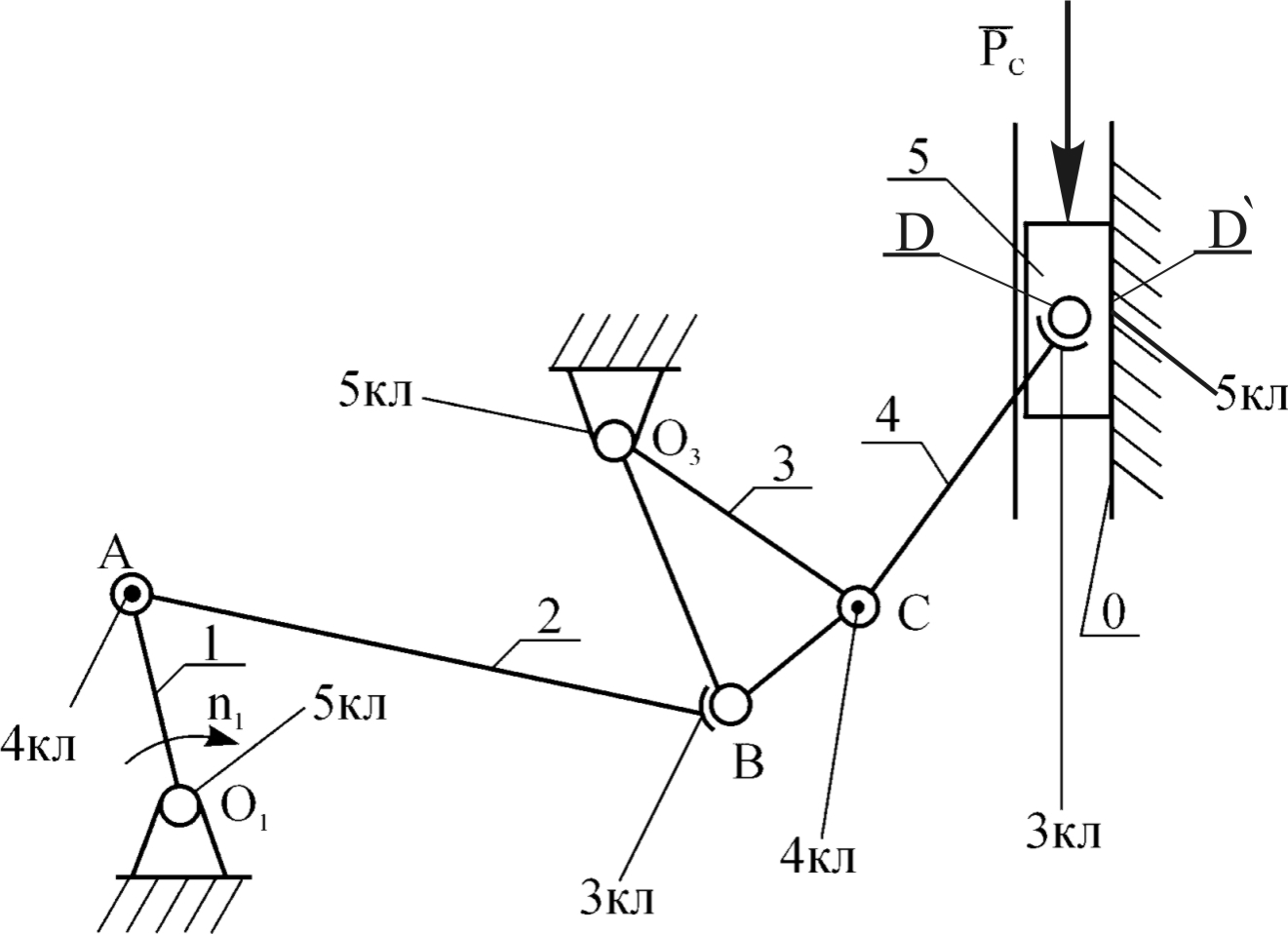
Рис. 1.15. Схема механизма компрессора без избыточных связей

2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМОВ

2.1. Задачи и методы
Под кинематическим исследованием механизмов понимают изучение движений звеньев механизма без учета их масс и сил, действующих на эти звенья. Для выполнения кинематического исследования должны быть заданы схема и размеры механизма, а также законы движения его ведущих звеньев. В результате исследования по заданному закону движения ведущих звеньев определяются положения, угловые скорости и ускорения ведомых звеньев, а также перемещения, скорости и ускорения их отдельных точек (центров кинематических пар, центров масс и т. д). Рассмотрим вначале два простых движения твердого тела.

---

Поступательным движением твердого тела называется такое движение, при котором любая прямая, неизменно связанная с телом, перемещается параллельно самой себе, оставаясь параллельно своему начальному положению (рис.2.1).

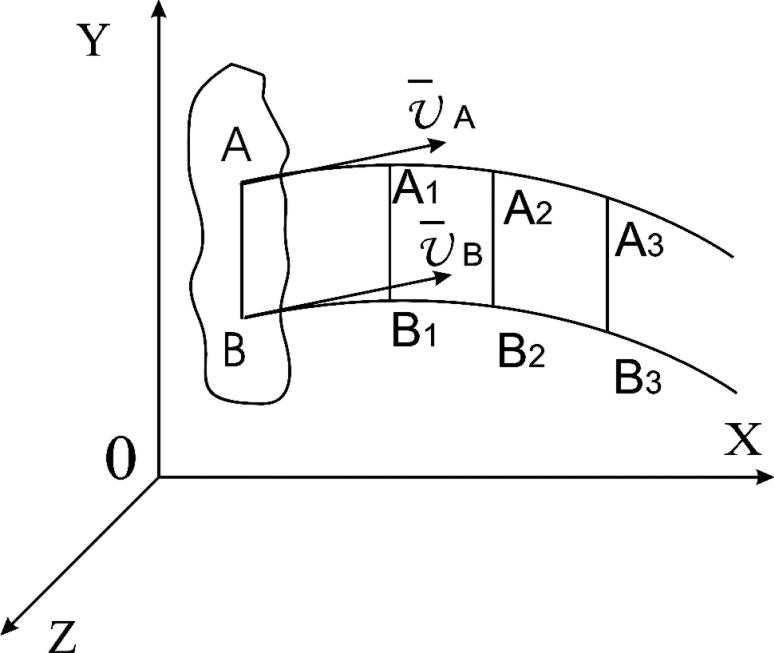
Рис.2.1. Поступательное движение
При поступательном движении все точки твердого тела описывают одинаковые траектории и в каждый момент имеют равные по модулю и направлению скорости и ускорения.

Если твердое тело движется так, что две какие-нибудь его точки остаются неподвижными, то такое движение называется вращательным. Неподвижная прямая, проходящая через две неподвижные точек, является осью вращения тела. Каждая точка, не лежащая на оси вращения, описывает при вращательном движении окружность, плоскость которой перпендикулярна оси вращения и центр которой лежит на этой оси (рис.2.2). Угол – угол поворота тела. Отсюда уравнение движения тела =f (t). Быстрота изменения угла поворота характеризуется угловой скоростью  =   [1/c]. Переход от частоты вращения n (об/мин) к угловой скорости осуществляется по формуле:  =  .

Когда угловая скорость тела постоянна (  = const), вращение – равномерное. Угол поворота равен t. Перемещение т.М .(рис.2.2,а).

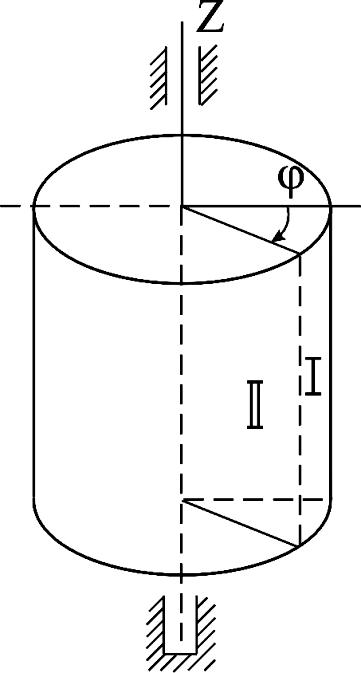
Рис.2.2. Вращательное движение

Линейная скорость т. М равна v= 

---

. Когда тело вращается неравномерно, то движение характеризуется угловым ускорением

,

т.е. первой производной угловой скорости по времени.

При ускоренном движении (рис.2.3,б) возникают касательное и нормальное ускорения соответственно равные

а
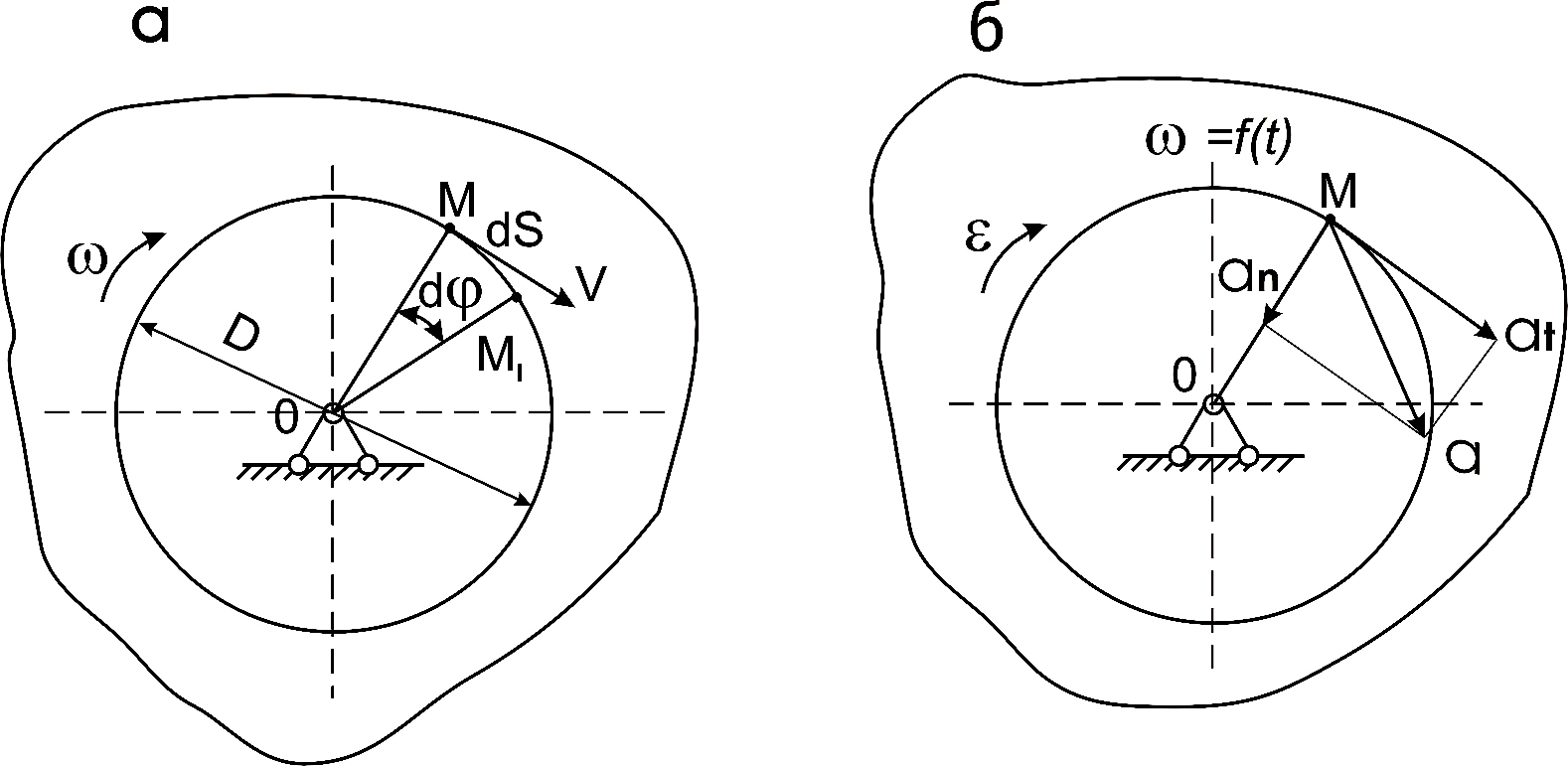
_t = ; а_n = = .

Рис.2.3. Вращение тела: а – равномерное, б – неравномерное

Полное ускорение равно а = = = r .

Направление полного ускорения определяется углом

.

Плоскопараллельным (или плоским) движением твердого тела называется такое движение, при котором все точки тела движутся параллельно какой-нибудь неподвижной (основной плоскости) (рис.2.4, а). Всякое движение плоской фигуры в её плоскости можно рассматривать как совокупность поступательного движения, определяемого движением произвольно выбранного полюса, и вращательного движения вокруг этого полюса.



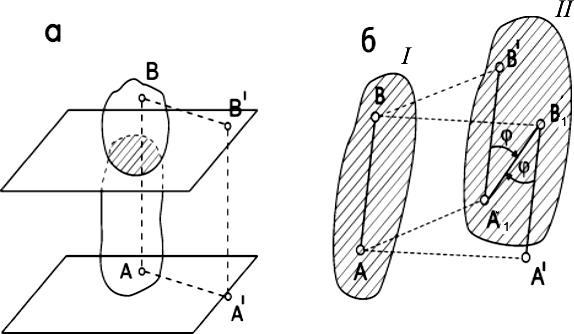
Рис.2.4. Плоскопараллельное движение
Рассмотрим перемещение плоской фигуры из положения I в положение II (рис.2.4,б). Определим положение фигуры отрезком АВ. Этот отрезок можно переместить из положения I в положение II. Перенеся его параллельно самому себе в положение А₁В′ (фигура совершит поступательное перемещение), а

---