Файл: Учебное пособие для студентов очной и заочной форм обучения Рекомендовано учебнометодическим объединением вузов рф по образованию в области транспортных машин и транспортнотехнологических.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 203
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
затем повернув отрезок вокруг точки А1 по часовой стрелки на угол φ (фигура совершит вращательное движение и займет положение II) так, чтобы точка В′ заняла свое положение В1. Можно также переместить фигуру поступательно из положения АВ в положение 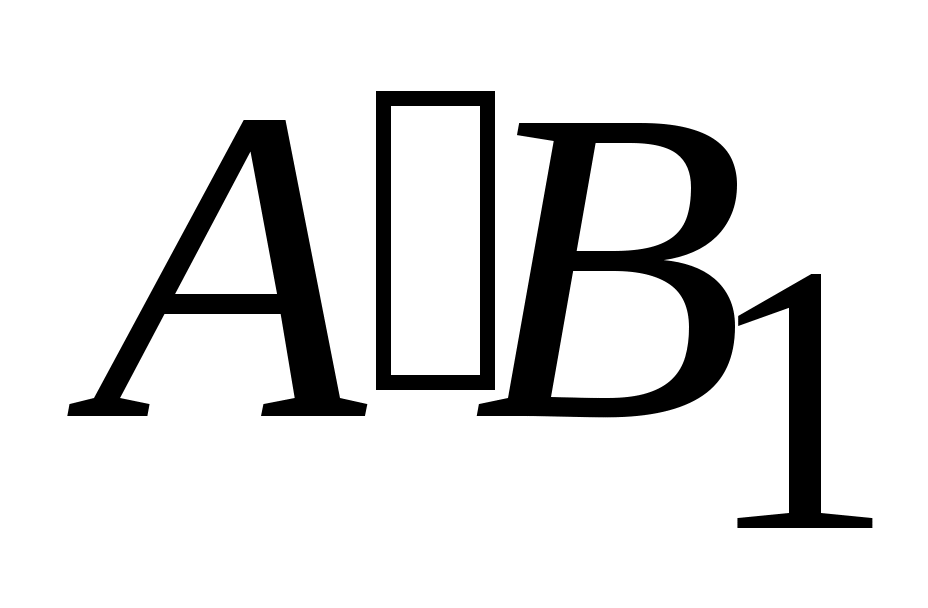 , а затем повернуть ее вокруг точки В1 на угол φ, чтобы точка
, а затем повернуть ее вокруг точки В1 на угол φ, чтобы точка  совпала с точкой А1.
совпала с точкой А1.
Поступательное перемещение зависит от выбора полюса, а величина угла поворота и направление поворота от выбора полюса не зависят.
Итак, плоскопараллельное движение можно разложить на два составляющих движения: поступательное вместе с некоторым полюсом т. М и вращательное вокруг этого полюса. Плоскопараллельное движение можно представить как сумму двух движений – поступательного и вращательного, то есть скорость любой точки тела равна геометрической (векторной) сумме скорости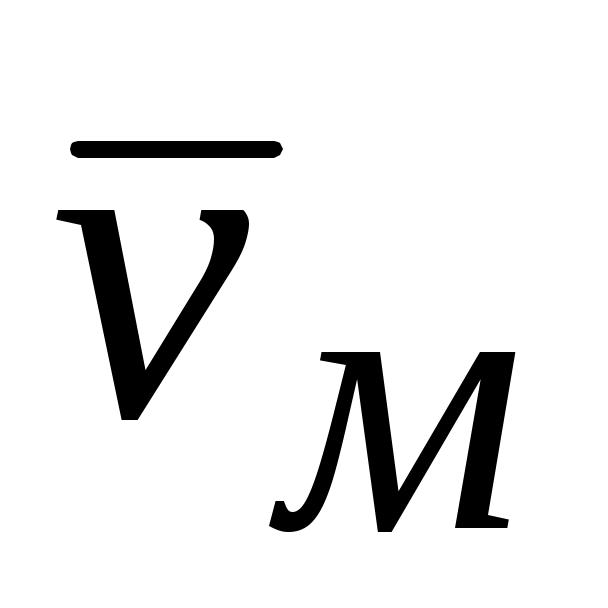 движения полюса (точка М) и скорости вращательного движения
движения полюса (точка М) и скорости вращательного движения 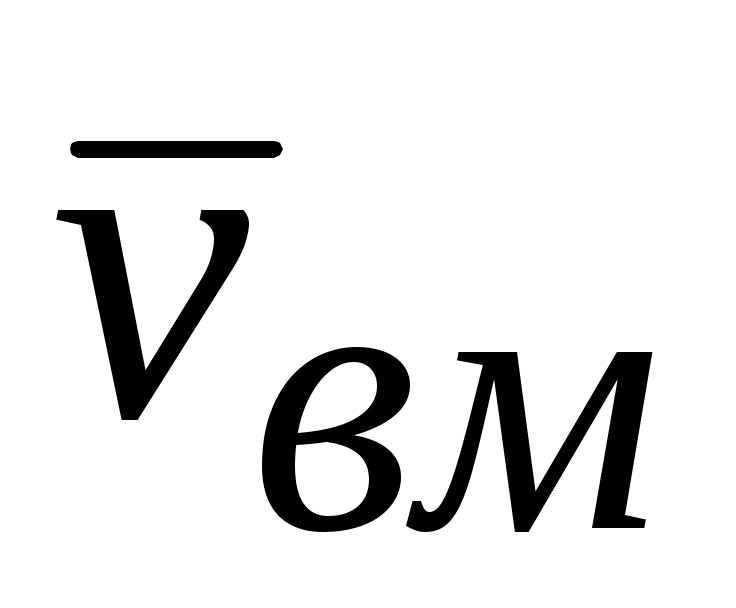 вокруг полюса М:
вокруг полюса М: 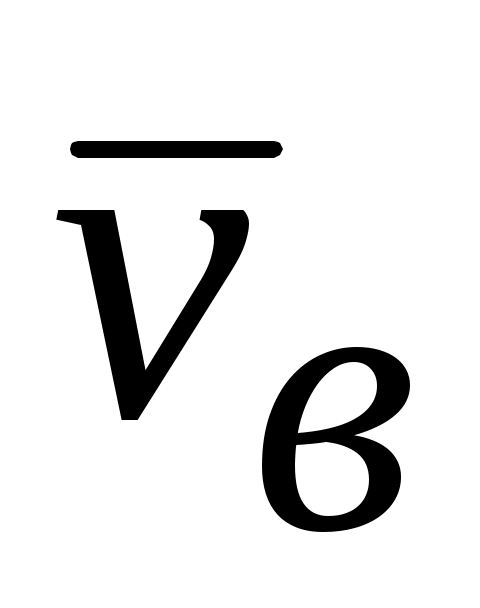 =
= 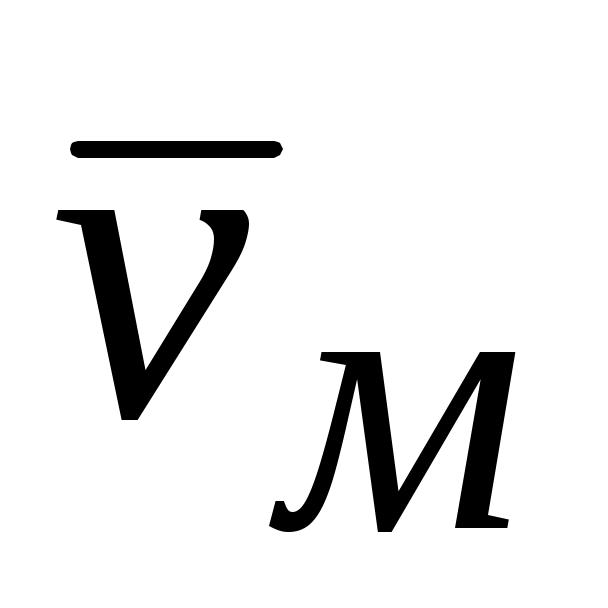 +
+ 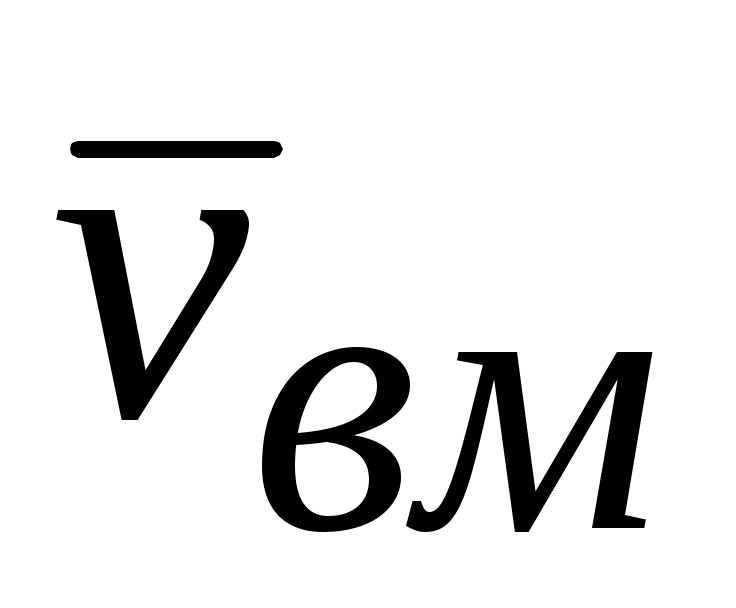 .
.
Скорость вращательного движения определяется по формуле
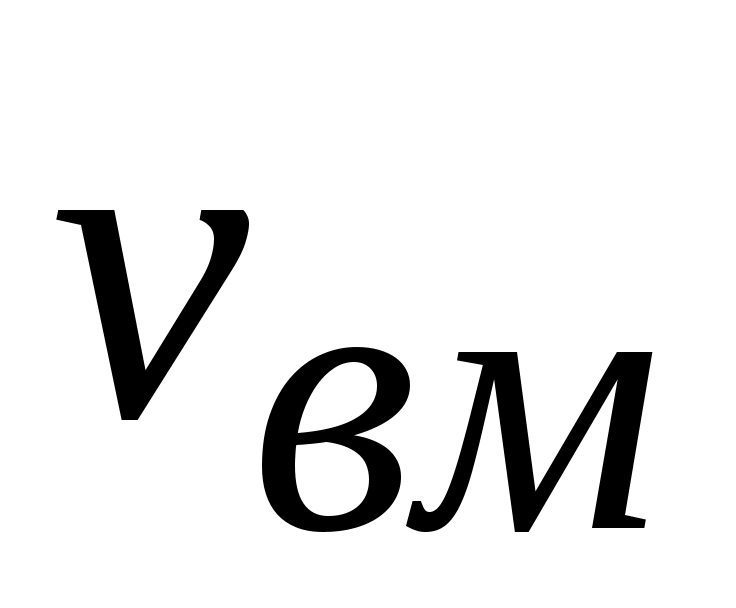 = ω
= ω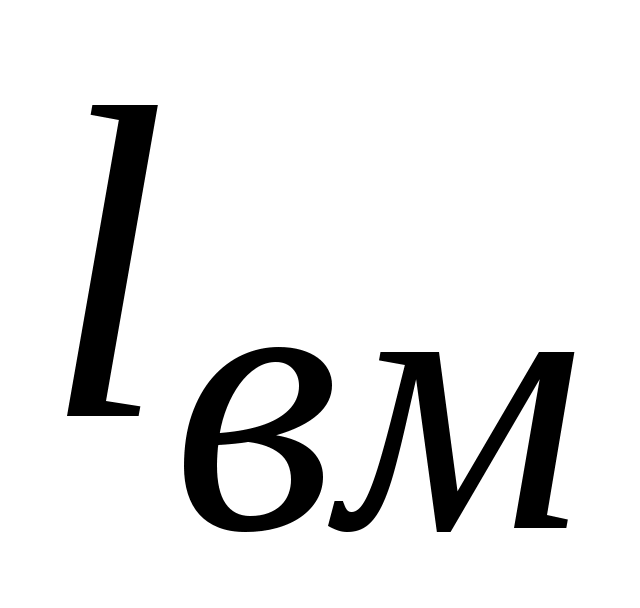 ,
,
где ω – угловая скорость вращения;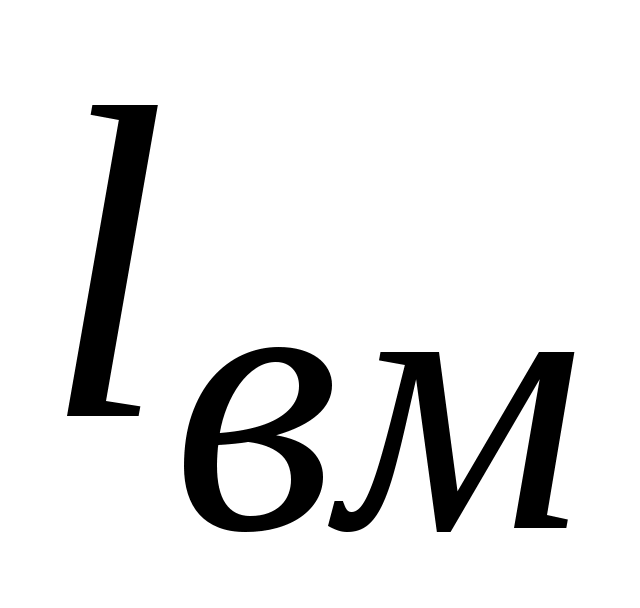 - радиус вращения точки В относительно полюса М. Скорость
- радиус вращения точки В относительно полюса М. Скорость 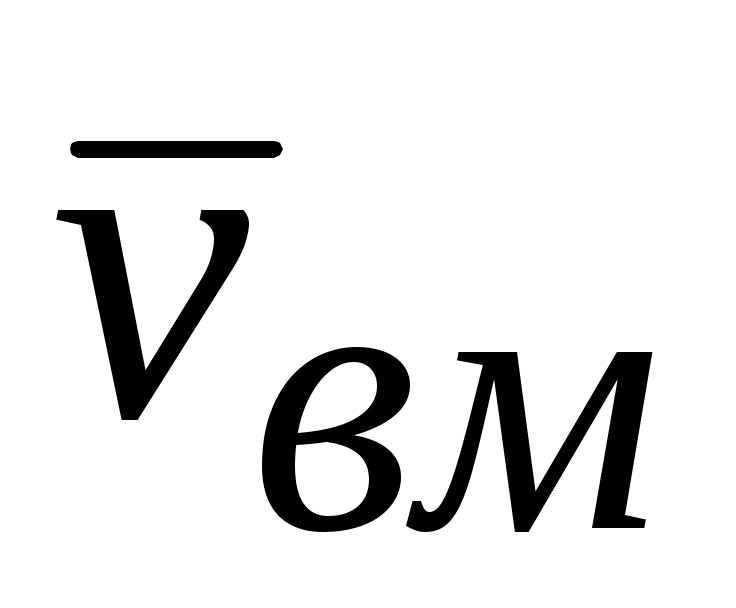 направлена перпендикулярно к радиусу вращения.
направлена перпендикулярно к радиусу вращения.
Из сказанного следует, что движение плоской фигуры в её плоскости будет определено, если для каждого момента времени известны значения функций
x =f1(t), y = f2(t) иφ = f3(t).
Примером плоскопараллельного движения является движение шатуна кривошипно-ползунного и четырехзвенного механизмов.
Основная задача кинематики в случае сложного движения состоит в том, чтобы, зная относительное и переносное движение точки, найти её абсолютное движение и определить траекторию, скорость и ускорение в этом движении.
Различают относительную, переносную и абсолютные скорости и ускорения точки. Абсолютная скорость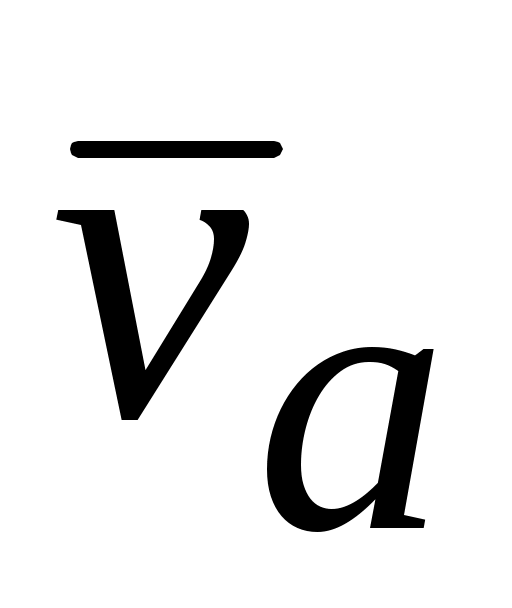 и абсолютное ускорение
и абсолютное ускорение  точки вызваны движением относительно неподвижной системы отсчета. Относительная скорость
точки вызваны движением относительно неподвижной системы отсчета. Относительная скорость 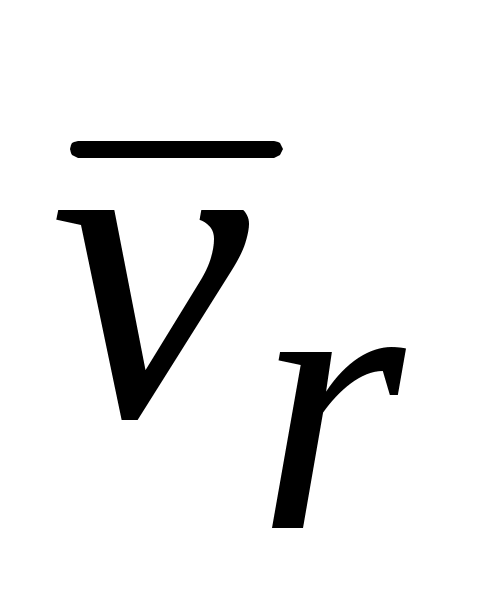 и относительное ускорение
и относительное ускорение 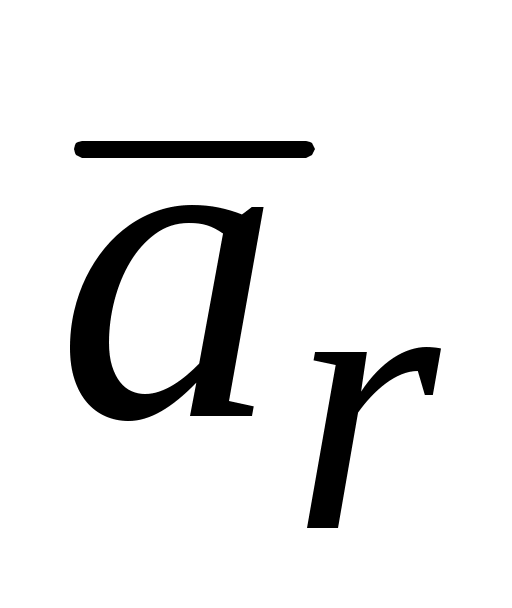 обусловлены движением по отношению к подвижной системе координат. Согласно теореме о сложении скоростей имеем, что абсолютная скорость точки равна геометрической сумме её переносной
обусловлены движением по отношению к подвижной системе координат. Согласно теореме о сложении скоростей имеем, что абсолютная скорость точки равна геометрической сумме её переносной 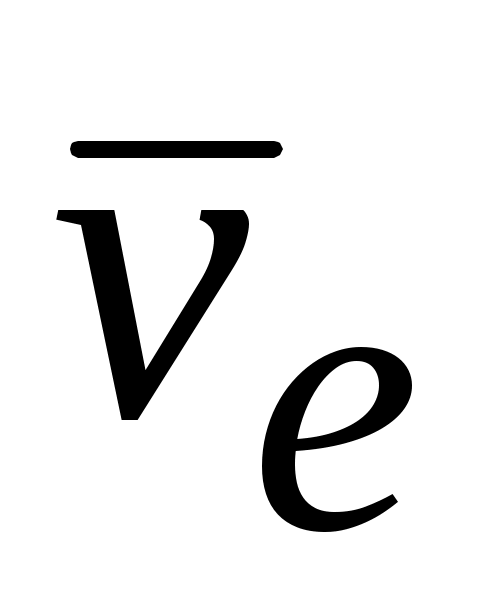 и относительной
и относительной 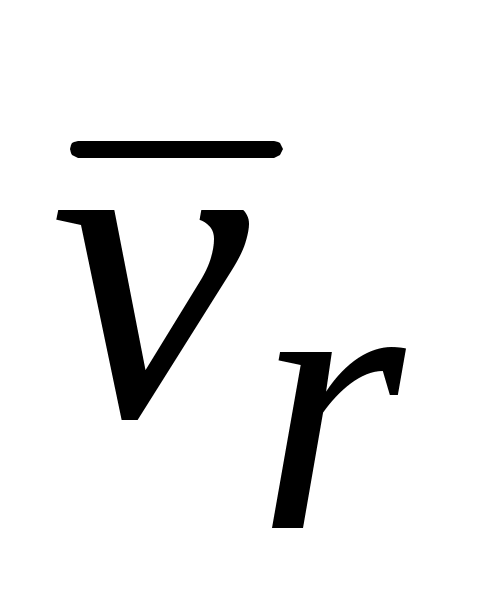 скоростей. Эту теорему называют правилом параллелограмма или треугольника скоростей. Абсолютное движение точки (или тела) можно назвать также сложным или результирующим движением, как результат сложения относительного и переносного движения.
скоростей. Эту теорему называют правилом параллелограмма или треугольника скоростей. Абсолютное движение точки (или тела) можно назвать также сложным или результирующим движением, как результат сложения относительного и переносного движения.
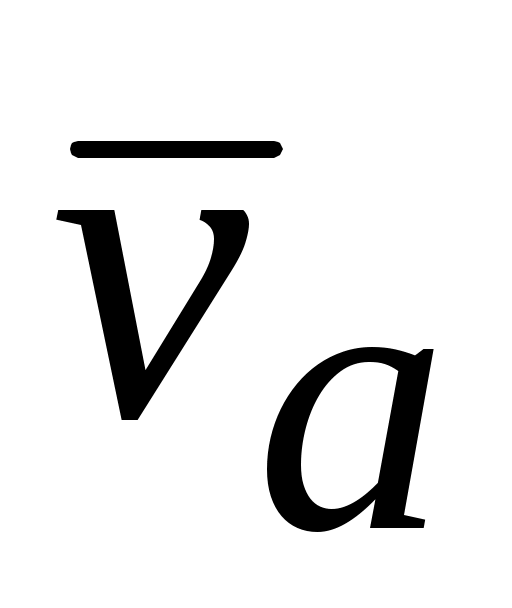 =
= 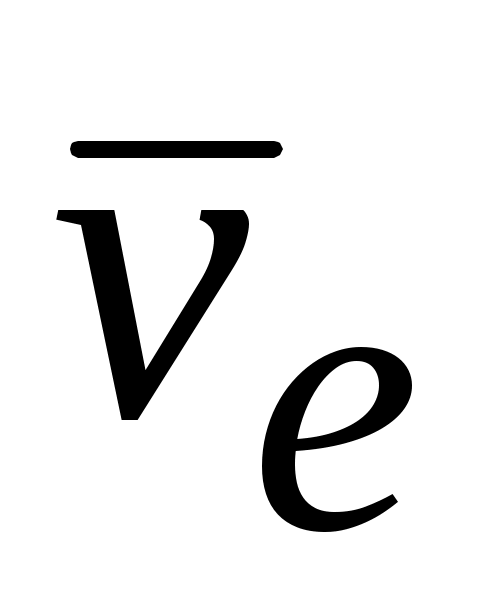 +
+ 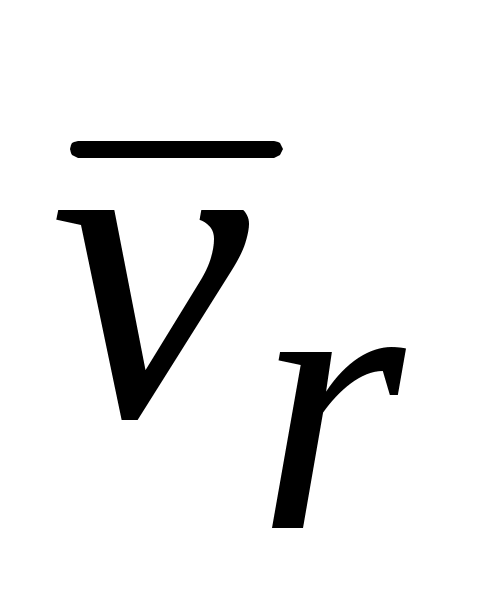 .
.
Абсолютное ускорение при переносном вращательном движении определяется зависимостью
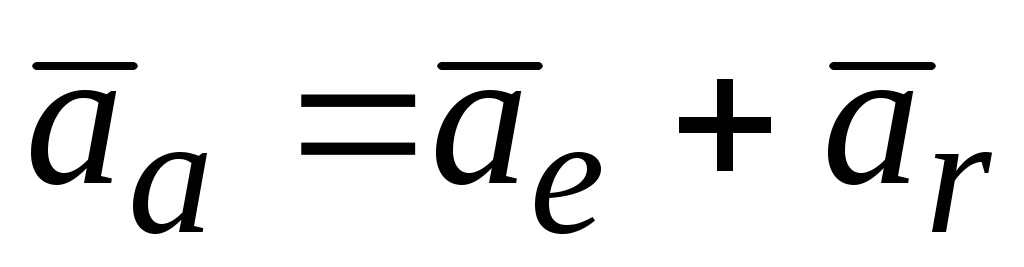 +2(
+2(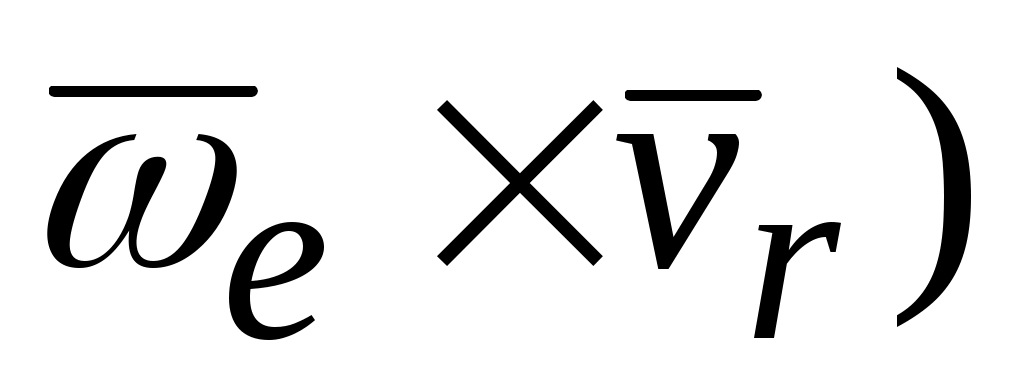
Здесь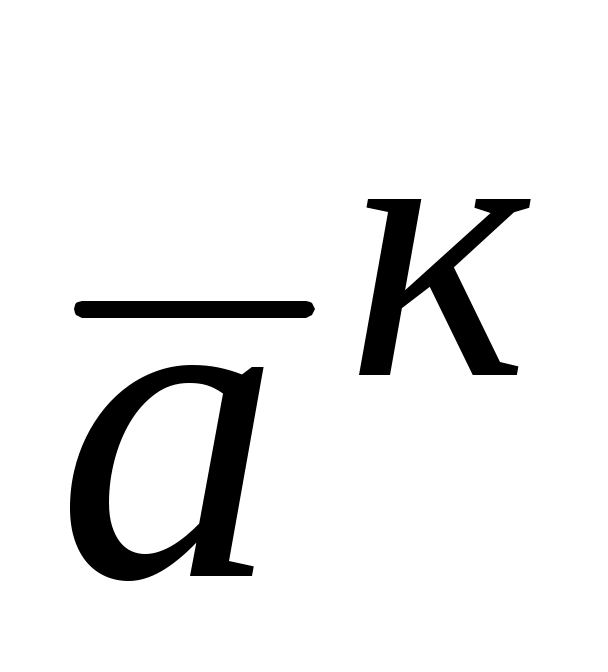 = 2(
= 2(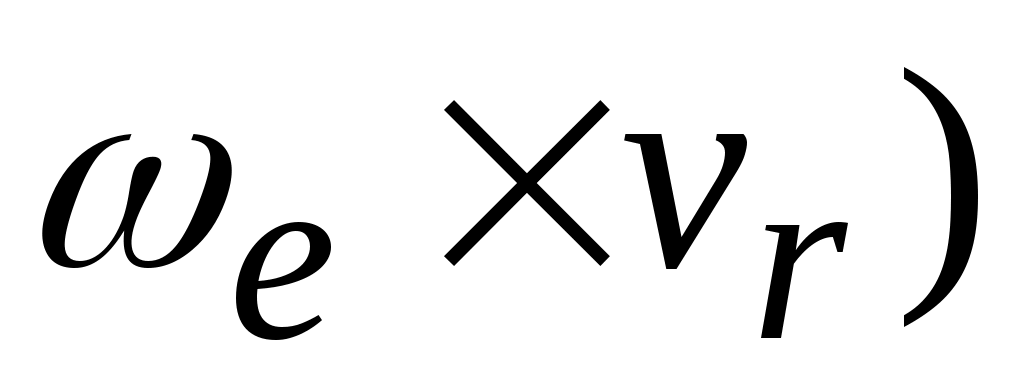 – поворотное ускорение точки (ускорение Кориолиса).
– поворотное ускорение точки (ускорение Кориолиса).
При поступательном переносном движении ускорение Кориолиса равно нулю и
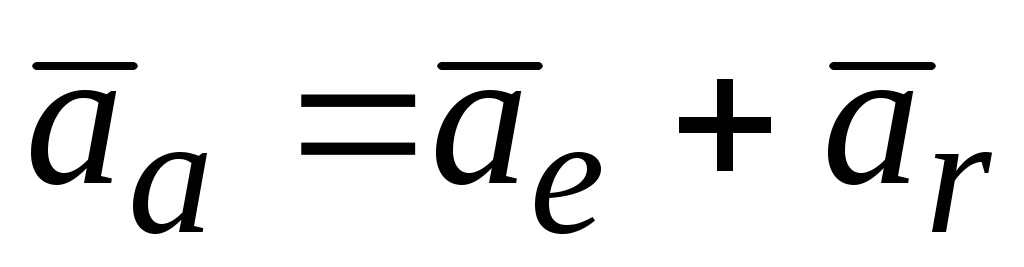 .
.
При плоском движении направление ускорения Кориолиса определяется поворотом вектора относительной скорости на 900 в направлении переносного вращения. Действительно, в общем случае три вектора
1.Векторы, выходящие из полюсов планов (скоростей и ускорений) соответствуют масштабным отрезкам абсолютных скоростей и ускорений
соответствующих точек. Концы этих векторов обозначаются в планах скоростей – а, в, с, в планах ускорений –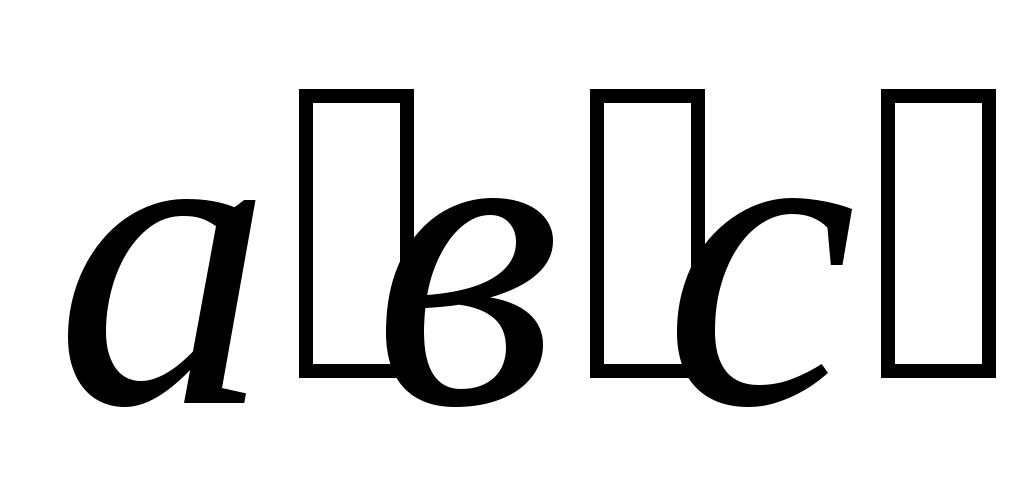 и носят название вершин планов.
и носят название вершин планов.
2.Отрезки, соединяющие вершины планов соответствуют относительным скоростям ( ускорениям.).
3.Одоименные отрезки и фигуры на схеме механизма и на планах скоростей (ускорений) пропорциональны, подобны и повернуты соответственно на углы 90 (план скоростей) и 180 –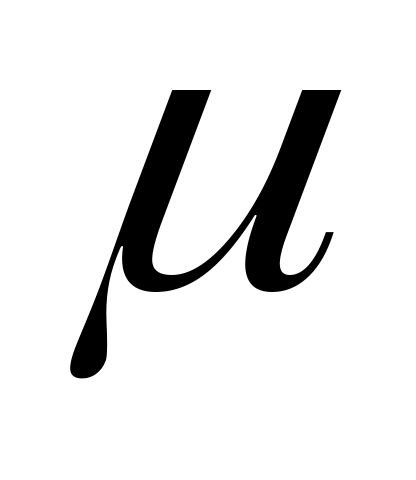 (план ускорений), где
(план ускорений), где 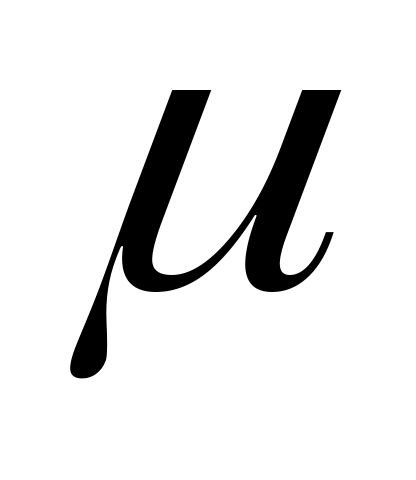 = arctg
= arctg 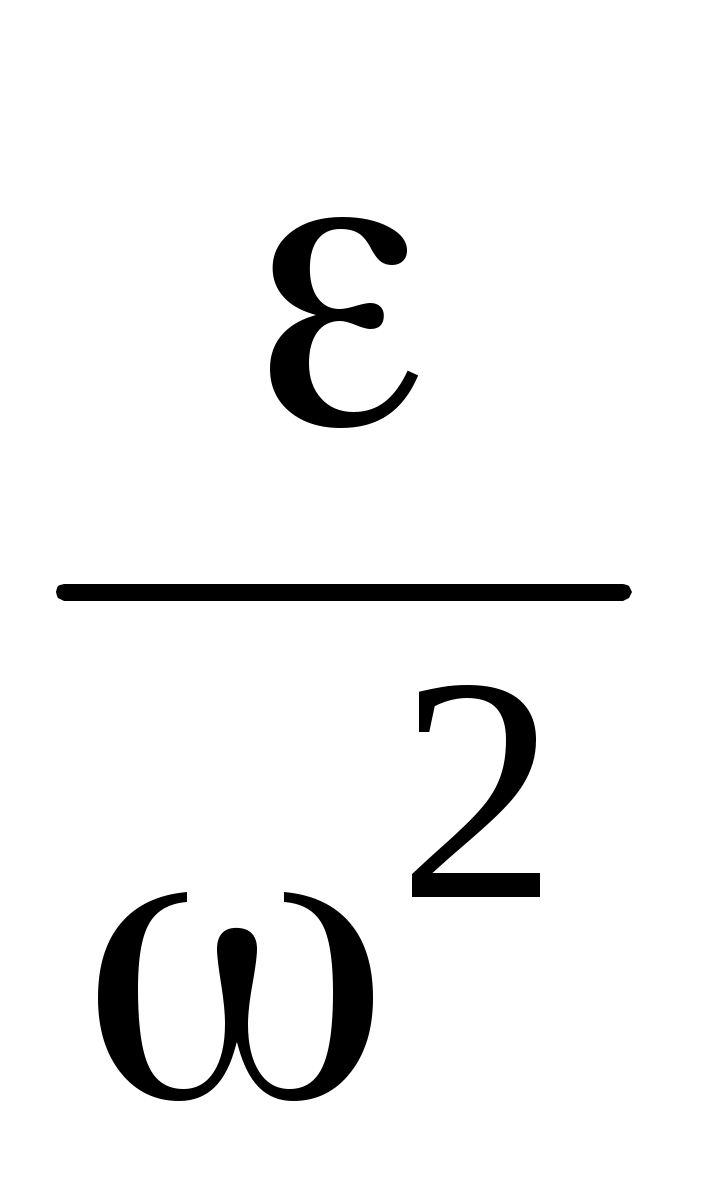 .
.
4.Точки, скорости (ускорения) которых равны нулю, располагаются в полюсе плана скоростей (ускорений).
Покажем кинематическую схему заданного механизма в соответствии с заданными размерами и (начальным) углом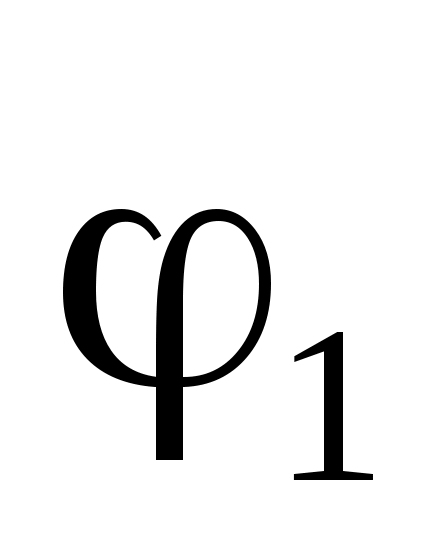 положения кривошипа. Принимаем масштабный коэффициент построения схемы механизма таким, чтобы она разместилась на отведенном поле чертежа. Следует учитывать расстояния между наиболее удаленными точками схемы механизма по вертикали и горизонтали. Построение планов скоростей и ускорений начинаем со звеньев, закон движения которых известен.
положения кривошипа. Принимаем масштабный коэффициент построения схемы механизма таким, чтобы она разместилась на отведенном поле чертежа. Следует учитывать расстояния между наиболее удаленными точками схемы механизма по вертикали и горизонтали. Построение планов скоростей и ускорений начинаем со звеньев, закон движения которых известен.
Пример 1
Схема поперечно-строгального станка (см. рис.1.4). Исходные данные: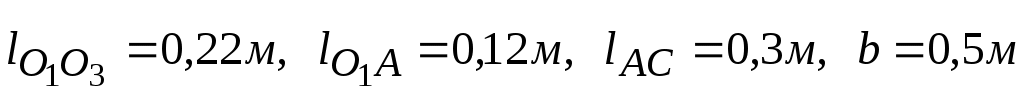 .
.
Масштаб построения будет определять размер b. Находим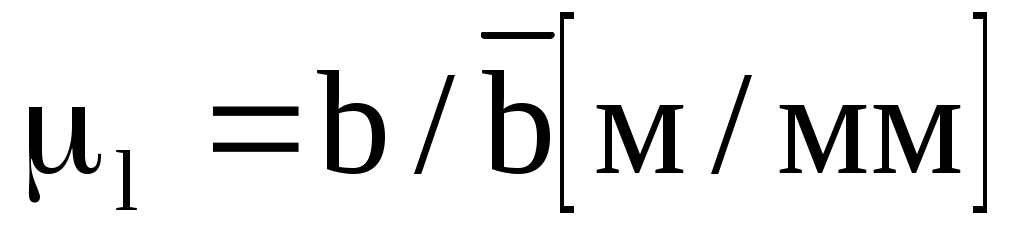 , где b – истинный (заданный) размер в м,
, где b – истинный (заданный) размер в м, 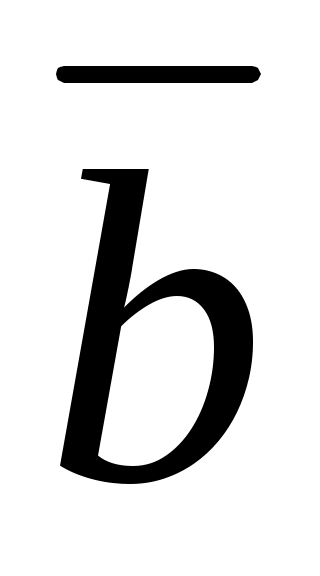 – выбранный масштабный отрезок в мм. Принимаем
– выбранный масштабный отрезок в мм. Принимаем 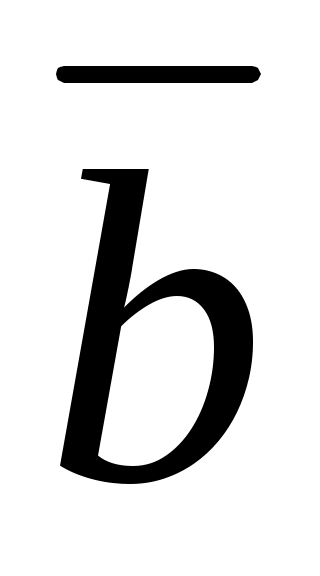 =100 мм. Получаем масштабный коэффициент плана положений
=100 мм. Получаем масштабный коэффициент плана положений 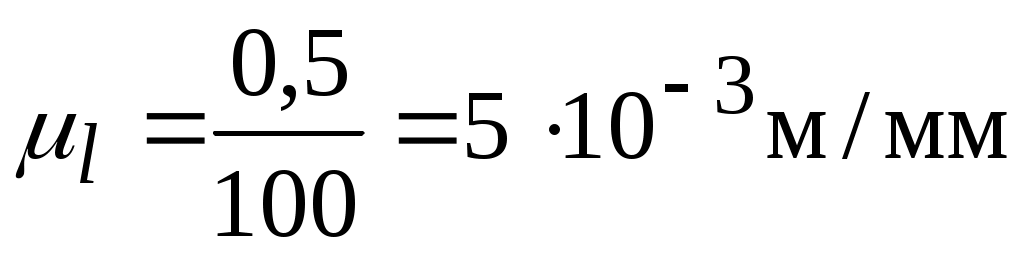
. Размеры остальных звеньев в мм равны
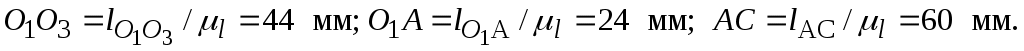
Изображаем в масштабе схему механизма (рис. 2.5).
Отмечаем положение неподвижных точек ,
,  и направление движения ползуна 5. На окружности
и направление движения ползуна 5. На окружности 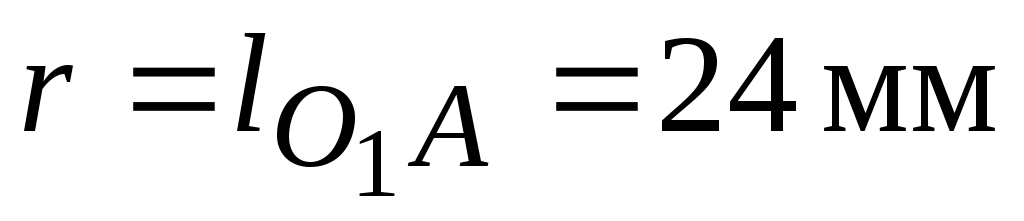 отмечаем точку А, определяемую заданным углом
отмечаем точку А, определяемую заданным углом 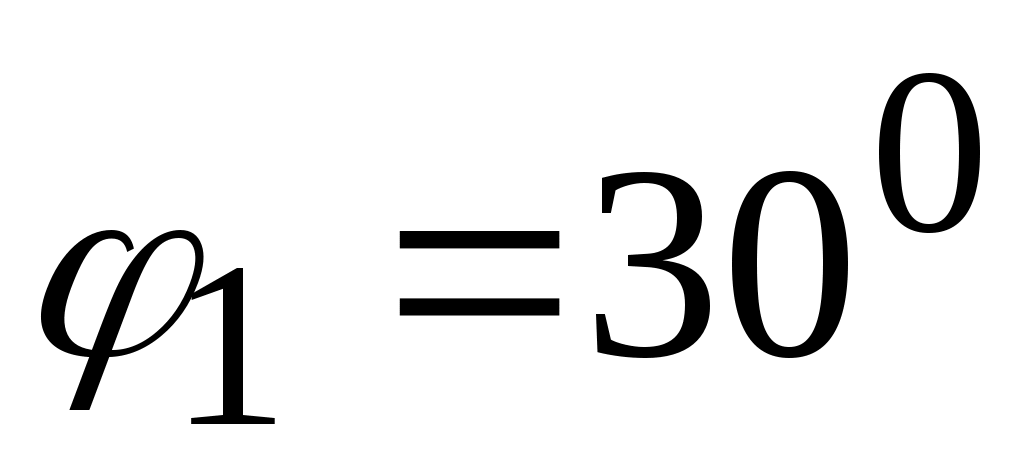 , отсчитываемым от горизонтального положения кривошипа. Находим положение точки С, отложив от точки А на продолжении прямой
, отсчитываемым от горизонтального положения кривошипа. Находим положение точки С, отложив от точки А на продолжении прямой 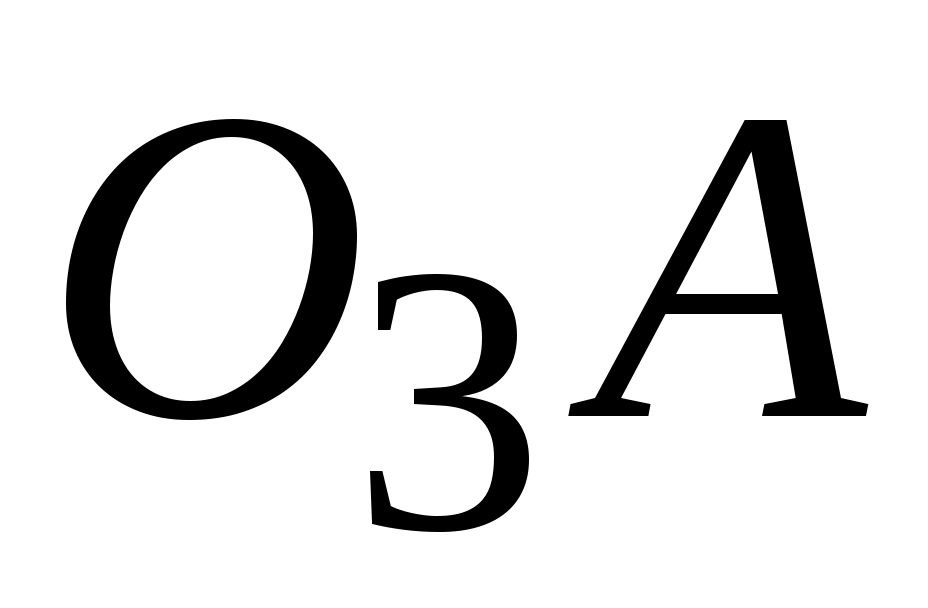 расстояние АС = 60 мм. Через точку С проводим вертикальную прямую до пересечения с линией хода ползуна (штока) и находим точку
расстояние АС = 60 мм. Через точку С проводим вертикальную прямую до пересечения с линией хода ползуна (штока) и находим точку 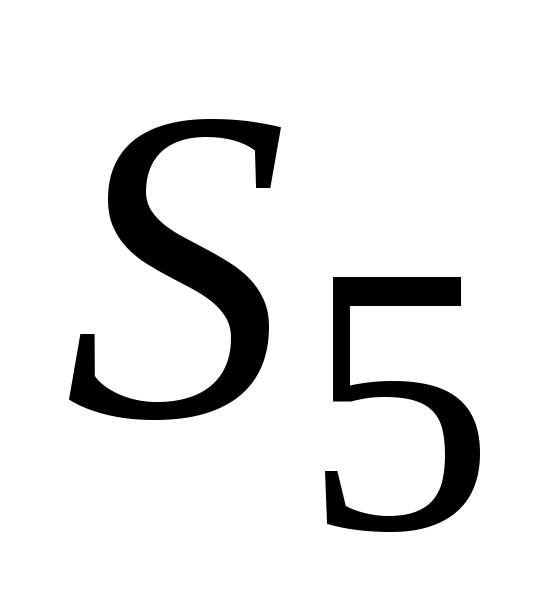 .
.
Пример 2
Схема брикетировочного автомата (рис. 1.6). Исходные данные:
 =0,23 м,
=0,23 м, 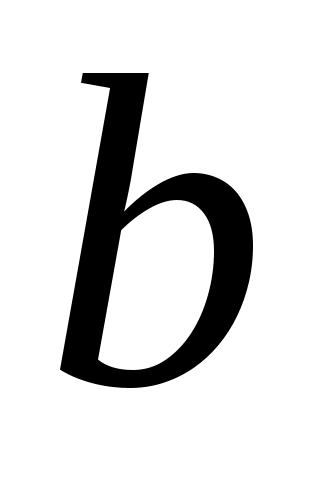 =0,41 м,
=0,41 м, 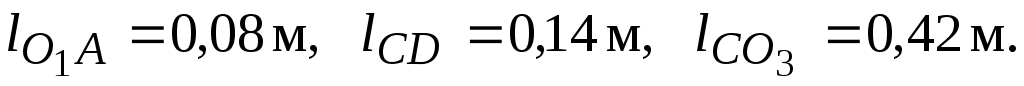
Находим масштабный коэффициент по наибольшему звену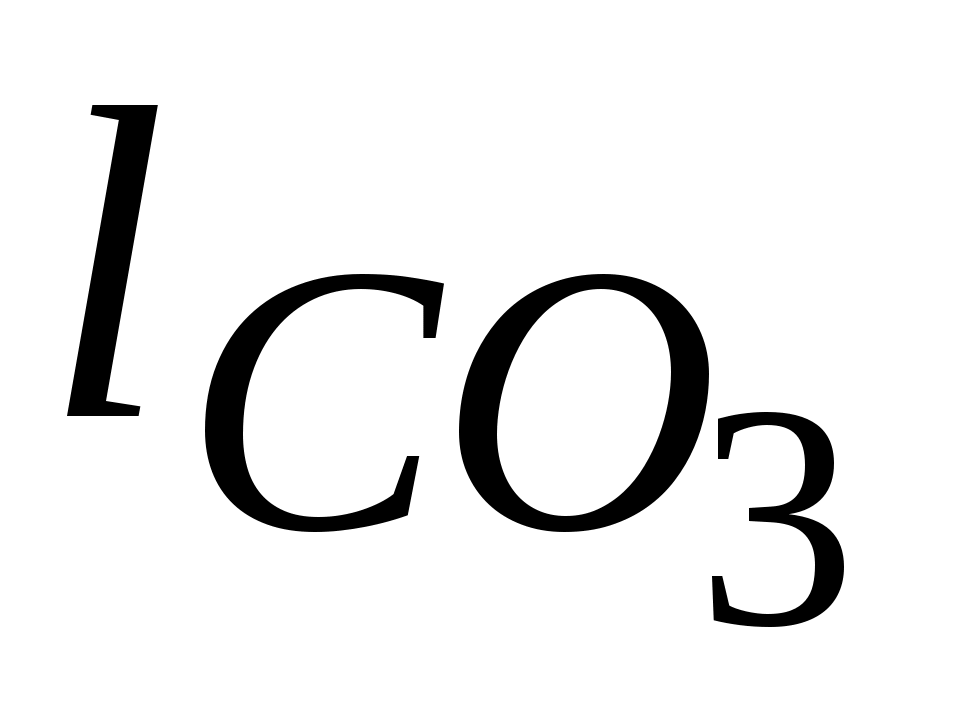 , принимая
, принимая 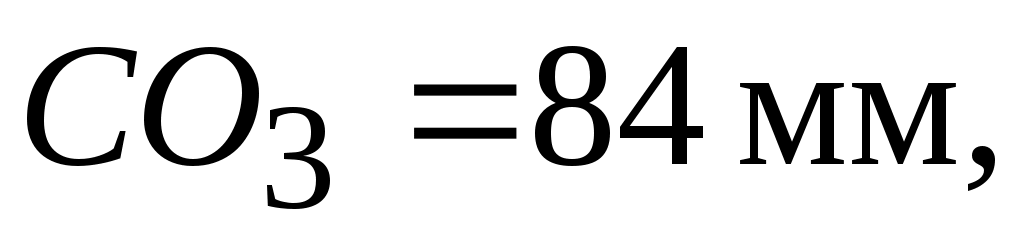 получим
получим 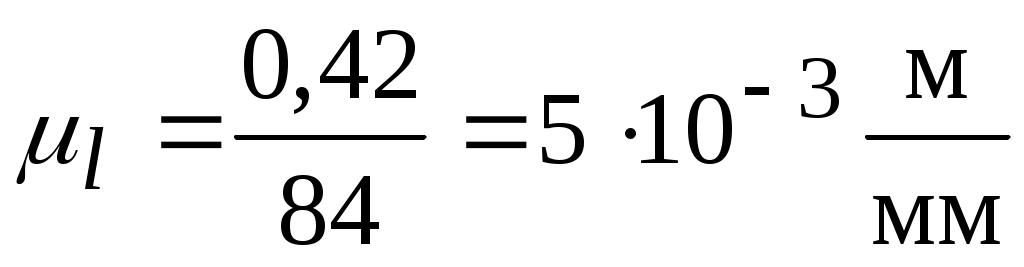 .
.
Определяем размеры других звеньев в масштабе:
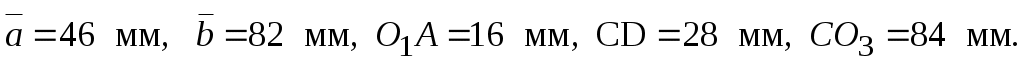
Отмечаем положение неподвижных точек О1, О3 (рис.2.8) и направление движения ползуна 5 параллельно оси О1Х. Проводим окружность радиусом О1А и находим на ней положение точки А в соответствии с заданным углом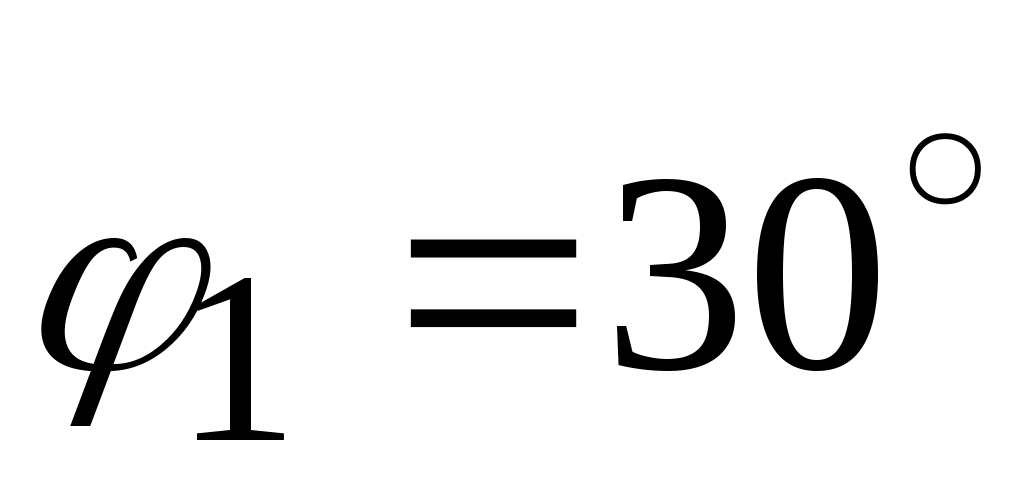 . Через точки О3 и А проводим прямую и находим положение точки С. Радиусом
. Через точки О3 и А проводим прямую и находим положение точки С. Радиусом 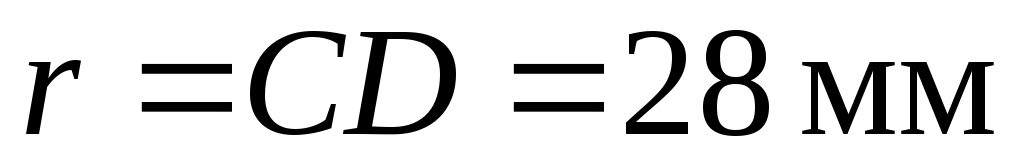
, из точки С делаем засечку на направлении движения ползуна 5 и получаем точку D.
Пример 3
Схема компрессора (рис.1.11). Исходные данные:
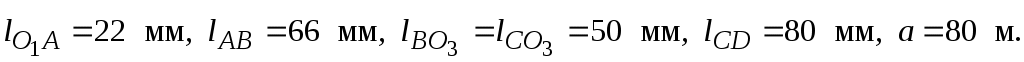
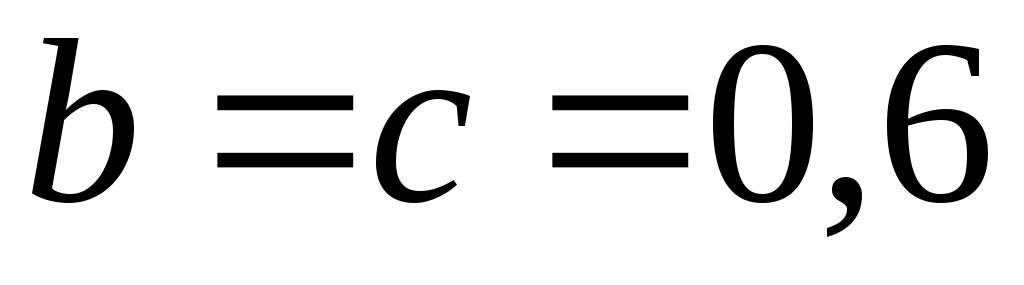 м. Находим
м. Находим  по размер
по размер 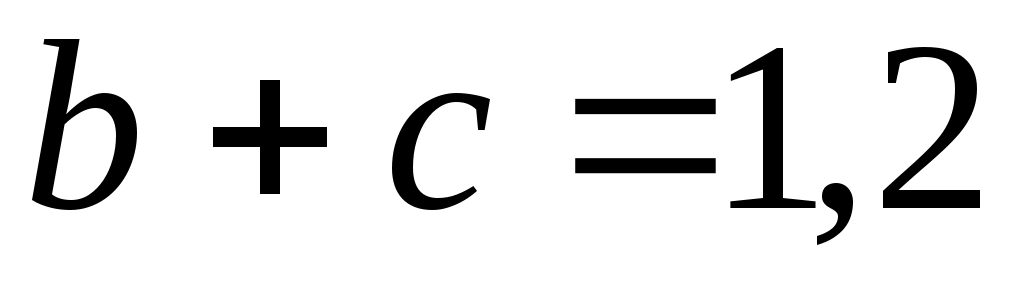 м.
м.
Получаем
Поступательное перемещение зависит от выбора полюса, а величина угла поворота и направление поворота от выбора полюса не зависят.
Итак, плоскопараллельное движение можно разложить на два составляющих движения: поступательное вместе с некоторым полюсом т. М и вращательное вокруг этого полюса. Плоскопараллельное движение можно представить как сумму двух движений – поступательного и вращательного, то есть скорость любой точки тела равна геометрической (векторной) сумме скорости
Скорость вращательного движения определяется по формуле
где ω – угловая скорость вращения;
Из сказанного следует, что движение плоской фигуры в её плоскости будет определено, если для каждого момента времени известны значения функций
x =f1(t), y = f2(t) иφ = f3(t).
Примером плоскопараллельного движения является движение шатуна кривошипно-ползунного и четырехзвенного механизмов.
Основная задача кинематики в случае сложного движения состоит в том, чтобы, зная относительное и переносное движение точки, найти её абсолютное движение и определить траекторию, скорость и ускорение в этом движении.
Различают относительную, переносную и абсолютные скорости и ускорения точки. Абсолютная скорость
Абсолютное ускорение при переносном вращательном движении определяется зависимостью
Здесь
При поступательном переносном движении ускорение Кориолиса равно нулю и
При плоском движении направление ускорения Кориолиса определяется поворотом вектора относительной скорости на 900 в направлении переносного вращения. Действительно, в общем случае три вектора 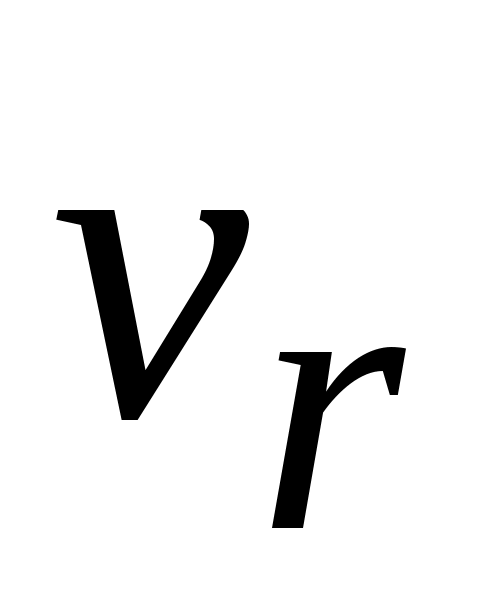 ,
, 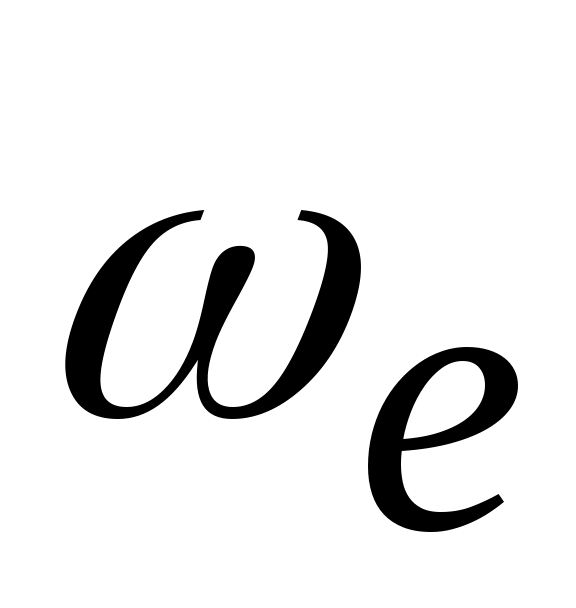 и
и 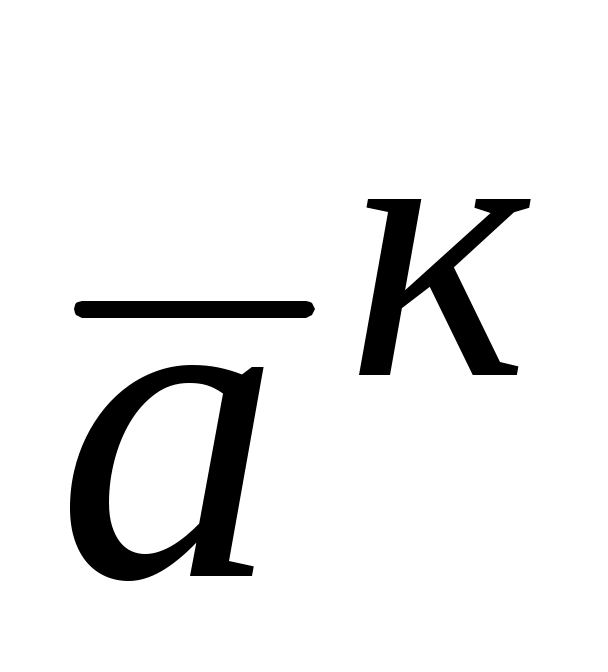 взаимно перпендикулярны. Если
взаимно перпендикулярны. Если 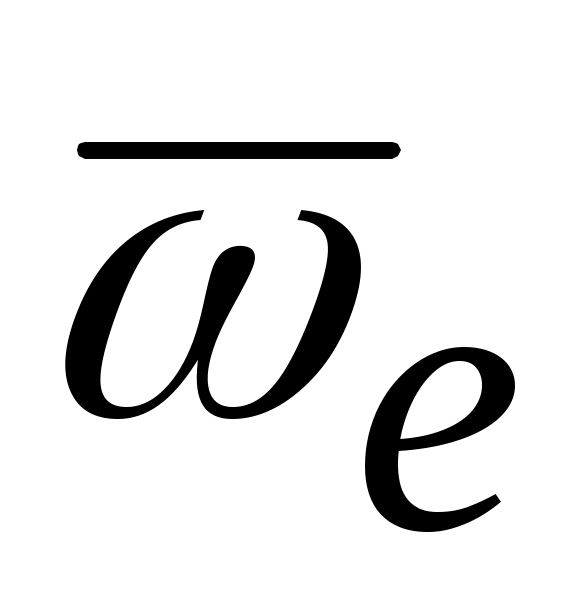
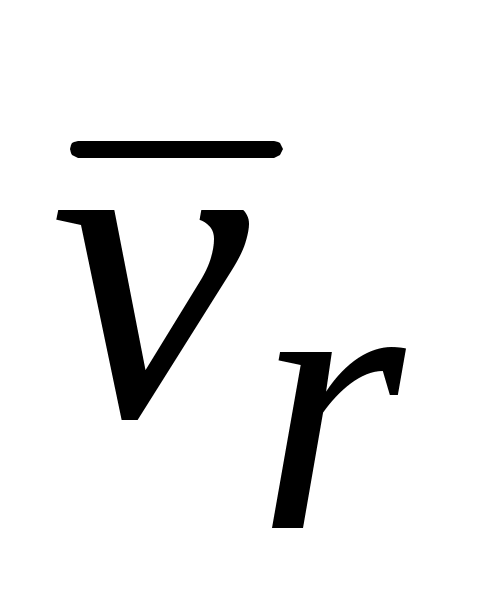 то sin(
то sin(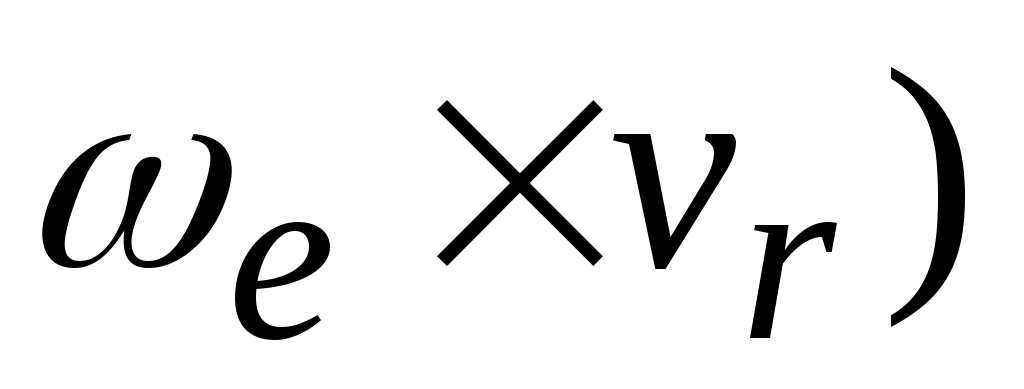 = 1, тогда
= 1, тогда
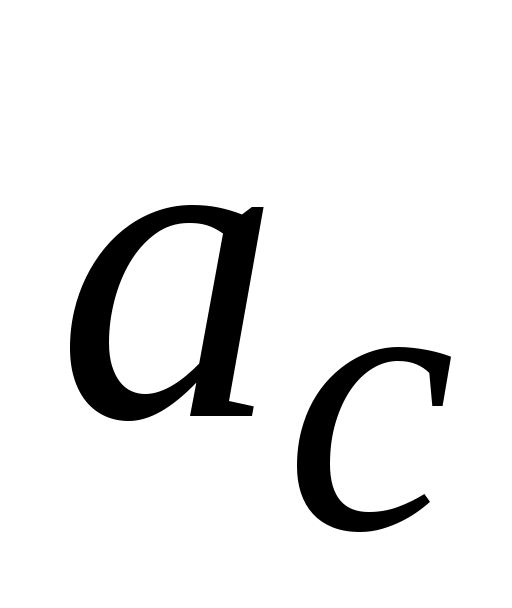 = 2
= 2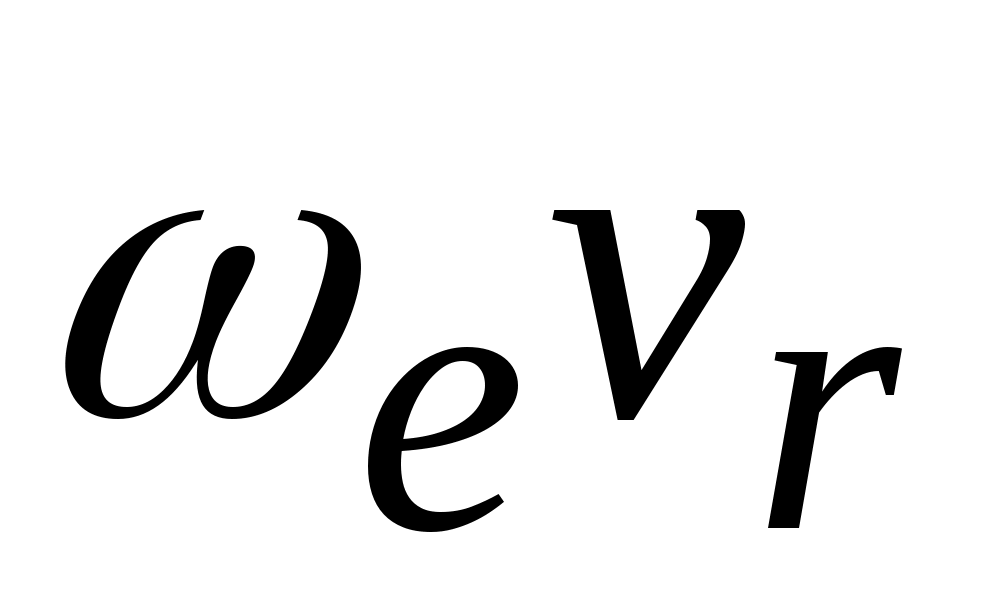 .
.
2.2. Свойства планов скоростей и ускорений
1.Векторы, выходящие из полюсов планов (скоростей и ускорений) соответствуют масштабным отрезкам абсолютных скоростей и ускорений
соответствующих точек. Концы этих векторов обозначаются в планах скоростей – а, в, с, в планах ускорений –
2.Отрезки, соединяющие вершины планов соответствуют относительным скоростям ( ускорениям.).
3.Одоименные отрезки и фигуры на схеме механизма и на планах скоростей (ускорений) пропорциональны, подобны и повернуты соответственно на углы 90 (план скоростей) и 180 –
4.Точки, скорости (ускорения) которых равны нулю, располагаются в полюсе плана скоростей (ускорений).
2.3. Примеры построения планов положений
Покажем кинематическую схему заданного механизма в соответствии с заданными размерами и (начальным) углом
Пример 1
Схема поперечно-строгального станка (см. рис.1.4). Исходные данные:
Масштаб построения будет определять размер b. Находим
. Размеры остальных звеньев в мм равны
Изображаем в масштабе схему механизма (рис. 2.5).
Отмечаем положение неподвижных точек
Пример 2
Схема брикетировочного автомата (рис. 1.6). Исходные данные:
Находим масштабный коэффициент по наибольшему звену
Определяем размеры других звеньев в масштабе:
Отмечаем положение неподвижных точек О1, О3 (рис.2.8) и направление движения ползуна 5 параллельно оси О1Х. Проводим окружность радиусом О1А и находим на ней положение точки А в соответствии с заданным углом
, из точки С делаем засечку на направлении движения ползуна 5 и получаем точку D.
Пример 3
Схема компрессора (рис.1.11). Исходные данные: