Файл: Учебное пособие для студентов очной и заочной форм обучения Рекомендовано учебнометодическим объединением вузов рф по образованию в области транспортных машин и транспортнотехнологических.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 205
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Статически определимой группой звеньев, для которой число уравнений равно числу неизвестных, является группа Ассура. Расчленяя механизм на группы Ассура, используя принцип освобождаемости от связей, можно определить все неизвестные силы и проверить работоспособность механизма. Законы изменения движущей силы или силы полезного сопротивления при проектировании задаются.
Порядок силового расчета следующий. Выделяют группы Ассура. Прикладывают к звеньям групп Ассура все силы и моменты сил в соответствии с принципом Даламбера – Лагранжа, включая реакции в КП на основе принципа освобождаемости от связи. Из уравнений статики для каждого звена группы находятся неизвестные составляющие для векторов сил. Последовательно рассматривая все группы Асура, переходят к силовому расчету начального звена. Определяется реакция в соединении начального звена со стойкой при наличии действия со стороны привода: уравновешивающей силы, когда движение передается через зубчатую передачу, или уравновешивающего момента, если начальное звено вращается через муфту.
3.2. Определение сил и моментов сил инерции
В динамических расчетах главный вектор сил инерции и главный момент в случае сложного движения звена определяется по формулам
М
где m – масса звена;
Для вычисления сил инерции надо определить ускорения аs и ε или из плана скоростей, или аналитически.
В частных случаях движения звеньев (поступательное или вращательное) остается или только главный вектор сил инерции, или главный момент сил. Аналитически силы инерции в плоском движении определяются как:
3.3. Величина и направление реакций
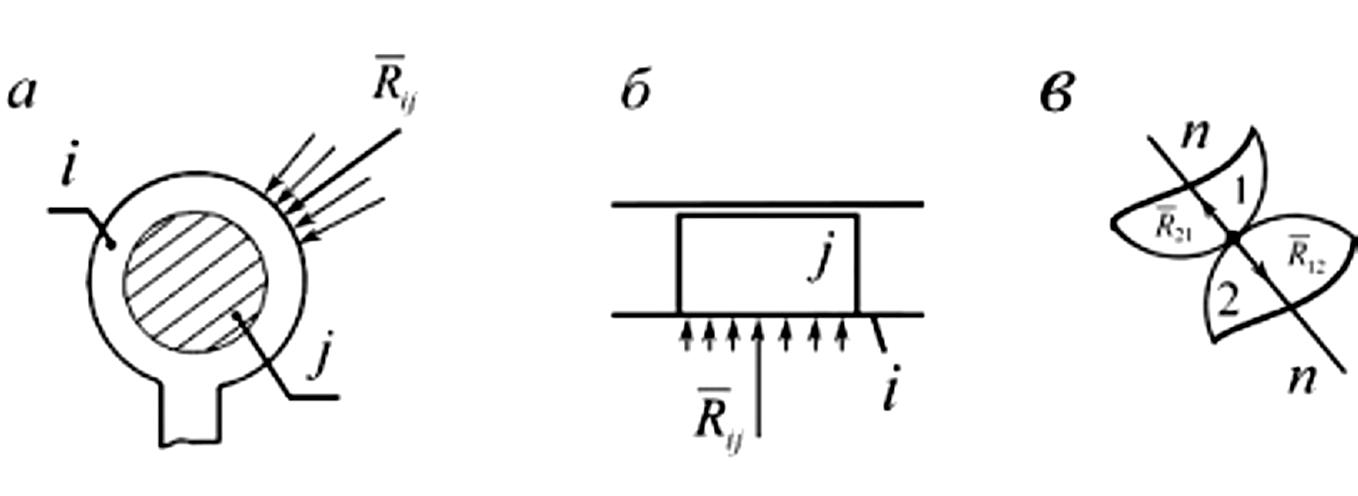
В плоских механизмах звенья могут образовывать низшие (вращательные и поступательные пары) и высшие кинематические пары, у которых касание элементов происходит либо в точке, либо по линии. Во вращательной паре без учета силы трения (рис.3.2,а) давление на цилиндрическую поверхность распределено по определенному закону, зависящему от степени приработанности поверхностей, смазки и т. д. Если силами трения пренебречь, то равнодействующая их проходит через центр шарнира О. Величина и направление силы
В высшей кинематической паре (рис.3.2,в) реакция нормальна к поверхности. Определению подлежит только её величина. И здесь число уравнений, которые нужно составить для определения реакций, совпадает с числом условий связи, накладываемых кинематической парой.
Если число звеньев в группе – n , то для них можно составить 3n уравнений равновесия. При соединении звеньев только кинематическими парами 5 класса число неизвестных реакций будет равно 2р5. Каждую силу можно определить в том случае, если число уравнений равновесия равно числу неизвестных компонентов сил, т.е. условием статической определимости групп звеньев при действии на них плоской системы сил является равенство
3n – 2р5 = 0.
Это условие совпадает с условием, которому удовлетворяют группы звеньев, именуемые группами Ассура.
Рис.3.2. Реакции в кинематических парах
3.4. Пример определения реакций в механизме
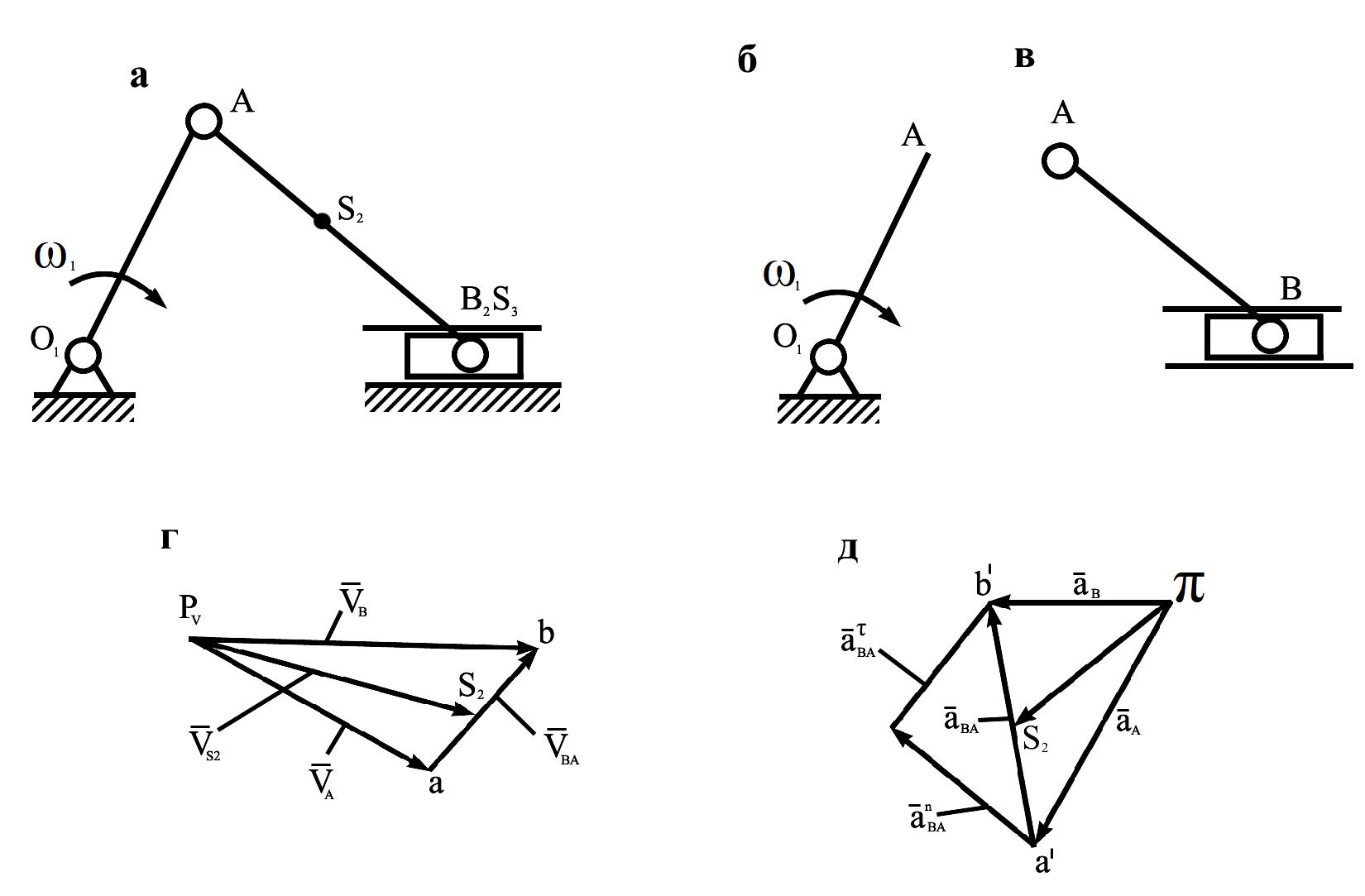
Рассмотрим пример определения реакций в кинематических парах кривошипно-ползунного механизма (рис.3.3). Предварительно строим планы скоростей и ускорений в соответствующих масштабах. Выделим в механизме двухповодковую группу Ассура ( звенья 2-3) и начальное звено 1. К группе Ассура приложим последовательно все внешние силы, силы и моменты сил инерции и реакции со стороны отброшенных звеньев и реакции в связанных кинематических парах. Внешние силы: силы тяжести
Составим сумму моментов сил
, действующих на 2-е звено (рис.3.4,а):
откуда находим величину реакции
Запишем векторные уравнения сил, действующих на 2-е и 3-е звенья, а затем их суммируем. Имеем
В последнем уравнении содержится две неизвестные: величины
Уравновешивающую силу, приложенную к зубчатому колесу, жестко связанному с начальным звеном, (рис.3.5,а) найдем, рассматривая его равновесие. Приложим все силы: реакцию
в = r1·cosα=(mz1/2)·cos20º.
Составим сумму моментов сил, действующих на начальное звено относительно точки О1 .
Отсюда находим
К
огда начальное звено приводится в движение от привода через муфту, то уравновешивающий момент Мур (рис.3.6, а) равен Мур=
Рис.3.3. Кривошипно-ползунный механизм
а – схема механизма, б – начальное звено, в – группа Ассура,
г – план скоростей, д –план ускорений
Р
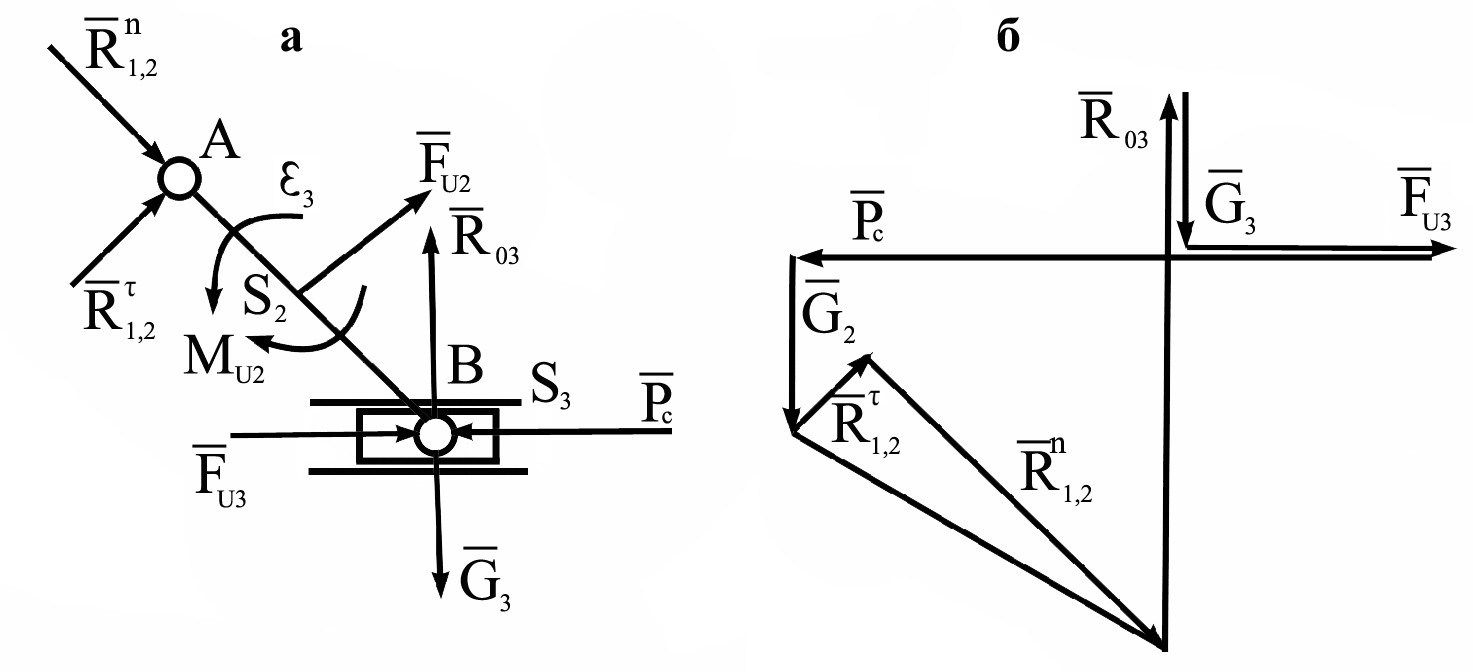
ис.3.4. Кинетостатика группы Ассура
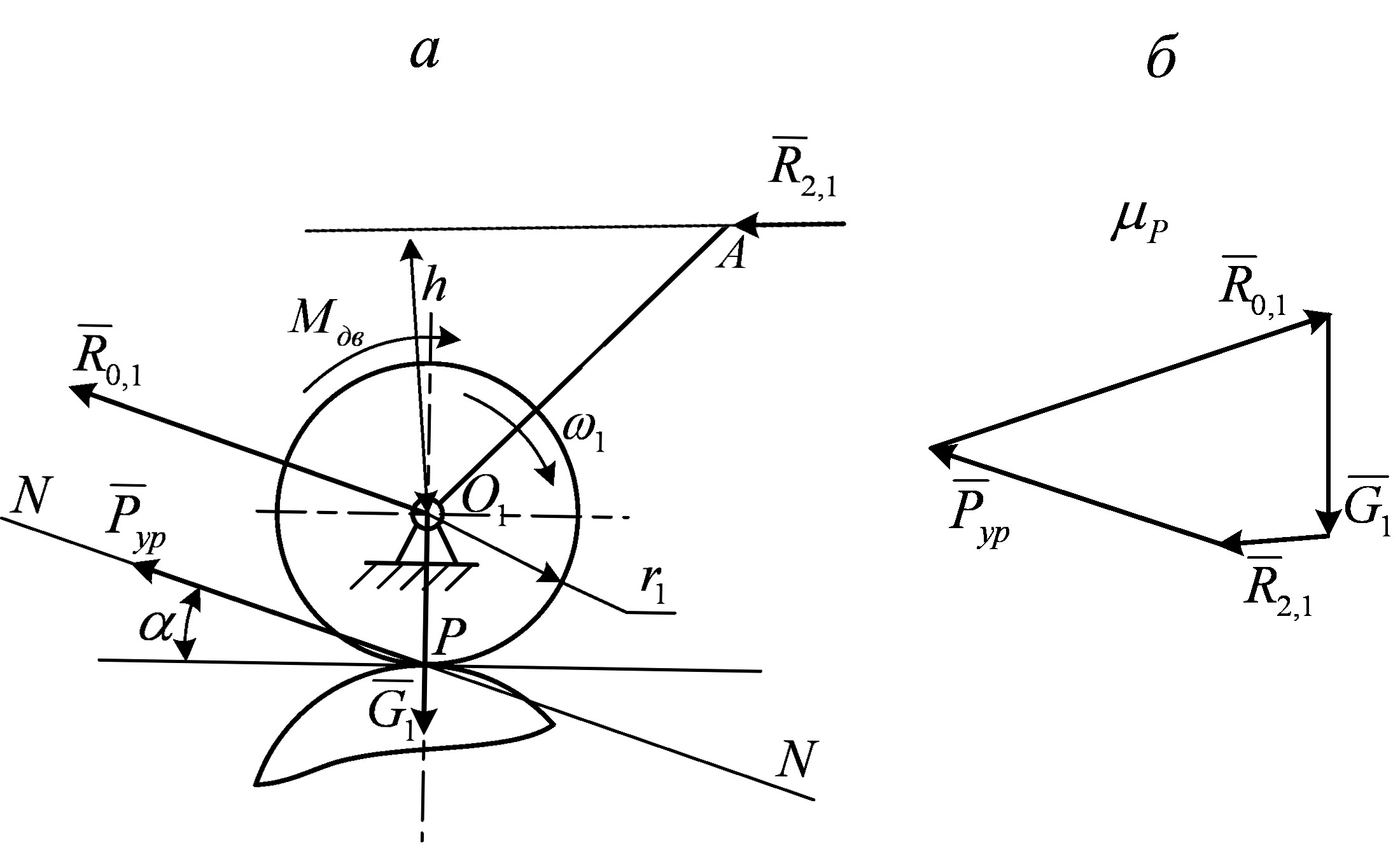
Рис.3.5. К определению уравновешивающей силы
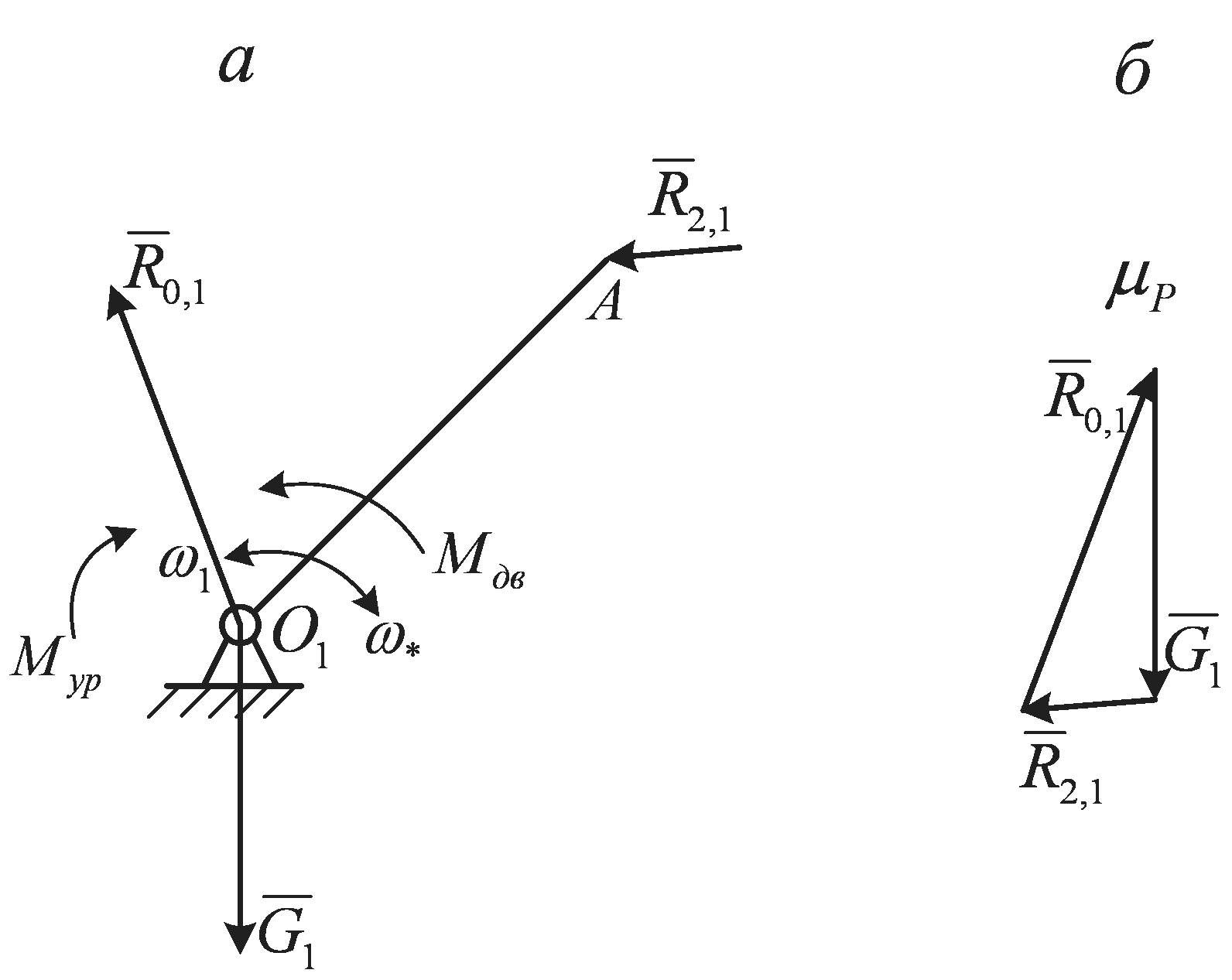
Рис.3.6. К определению уравновешивающего момента
4. Анализ движения машинного агрегата
Цель динамического анализа – определение истинного закона движения начального звена.
4.1. Динамическая модель машинного агрегата
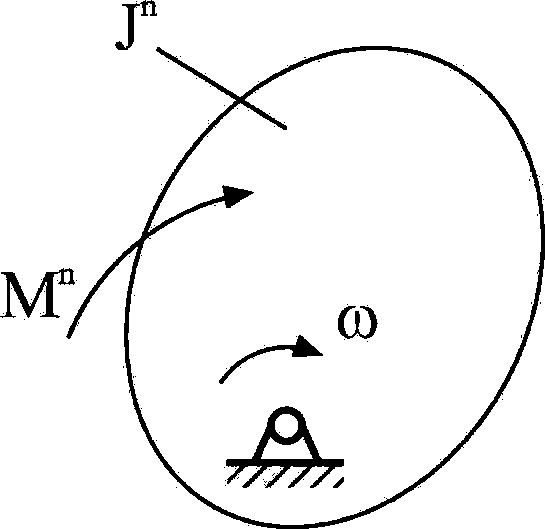
Рис. 4.1. Динамическая модель
Для упрощения решения задачи реальную схему машины заменяют динамической моделью. Простейшей моделью с одной степенью свободы с недеформированными звеньями и приводом от кривошипа является одномассовая система (рис. 4.1), обладающая некоторой условной массой, кинетическая энергия которой в любом положении звена приведения равна кинетической энергии всего механизма: