Файл: Учебное пособие для студентов очной и заочной форм обучения Рекомендовано учебнометодическим объединением вузов рф по образованию в области транспортных машин и транспортнотехнологических.doc

Пример 1

Схема механизма, построенного описанным выше методом, показана на рис. 2.5, а соответствующий план скоростей изображен на рис. 2.6.

Пусть задано =100 об/мин, тогда угловая скорость кривошипа .



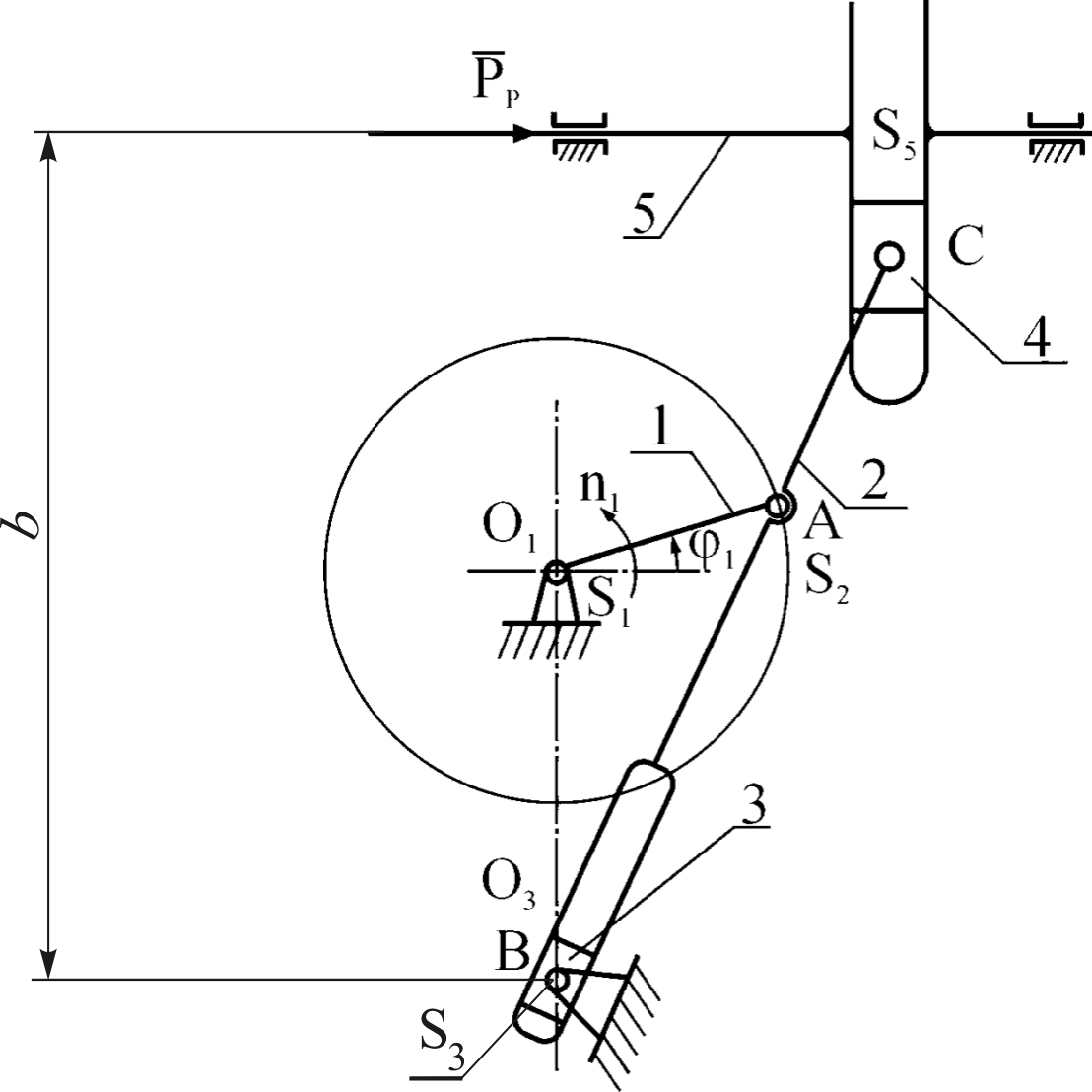
Рис. 2.5. Схема механизма



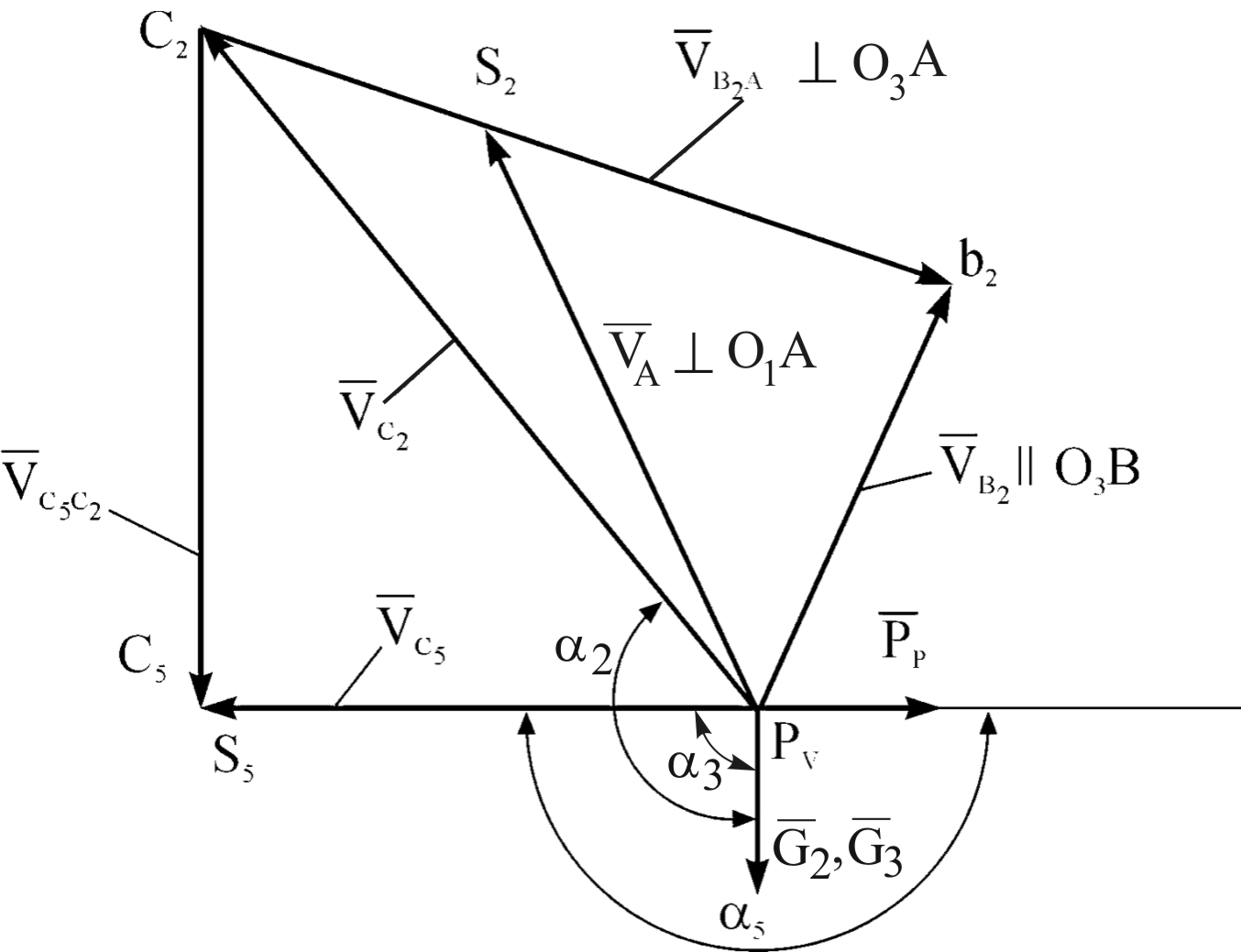
Рис. 2.6 План скоростей для поперечно-строгательного станка

Скорость точки А, принадлежащей одновременно первому и второму звену, . Задаемся длиной вектора , тогда масштабный коэффициент плана скоростей равен .

Рекомендуется принимать таким, чтобы содержал одну значащую цифру: 1,2 и 5 с нулями, тогда все вычисления можно выполнять устно, не используя вычислительную технику. Из произвольно выбранной точки (полюса плана скоростей) проводим отрезок перпендикулярно положению кривошипа О₁А в направлении угловой скорости (рис. 2.6). Для скорости точки В₂ векторные уравнения имеют вид:



или



Здесь – скорость неподвижной точки,

---

– скорость точки В₂относительно неподвижной точки В₀, то есть скорость в абсолютном движении, - скорость в относительном движении звена 2.

Решая последнее уравнение графически (через точку провести прямую, перпендикулярную звену ВС – направление вектора , а через точку – прямую, параллельную звену ВС – направление вектора ), получим точку . Отрезок соответствует скорости .

Скорость точки С можно определить, пользуясь свойством пропорциональности одноименных отрезков на плане положений механизма и на плане скоростей:



АС и АВ измеряемые на плане механизма, а – на плане скоростей.

На продолжении отрезка откладываем и получаем точку с₂.

Для скорости точки С₅пятого звена векторные уравнения имеют вид:



|| x || y

Решаем это уравнение графически. Из точки С₂ проводим прямую, перпендикулярную направлению движения штока 5, а из полюса – прямую, параллельную собственному движению. Получаем точку . Отрезок

---

соответствует в масштабе скорости точки С₃. Скорости центров масс S₂, S₅ равны скоростям соответственно точек А и С₅. Точки, скорости которых равны нулю, на плане скоростей находятся в полюсе .

Определяем величины скоростей.

;

; ; ,

где - отрезки в мм, снятые с плана скоростей.

Находим угловую скорость звена 2:

,

которая направлена против часовой стрелки.

Примечание: Приведенные выше значения отрезков в мм при вычислении скоростей, могут изменится после размножении пособия.

Пример 2

Схема механизма брикетировочного автомата построена на рис. 2.7, а план скоростей и ускорений соответственно на рис. 2.8 и рис.2.12.

Задано: =40 об/мин. Угловая скорость кривошипа

.

Построение планов начинаем с определения скоростей (ускорений) точек закон движения которых известен. Скорость точки А_1,2, принадлежит одновременно 1 и 2 звену камню равна

м/с

Задаемся длиной вектора и вычисляем масштабный коэффициент плана скоростей:

.

Из произвольно выбранной на чертеже точки (полюс плана скоростей) проводим линию перпендикулярно положению кривошипа О₁А (рис. 2.8) в направлении вращения кривошипа и откладываем на ней отрезок 66 мм. Составляем векторные уравнения для определения скоростей других точек. В абсолютном движении траектория т. А есть окружность радиуса

---

и может быть получена сложением переносного (вращение кулисы 3) и относительного (перемещения ползуна 2 вдоль кулисы движений (рис.2.9). На рисунке дуга АА` – траектория абсолютного движения, дуга АА′ при вращении кулисы – траектория переносного движения, перемещение по прямой А′А′′ вдоль кулисы – относительное движение. Таким образом, из точки А в абсолютном движении попадаем в точку А′′ выполняя два движения: поворачивая кулису и перемещая ползун вдоль неё.



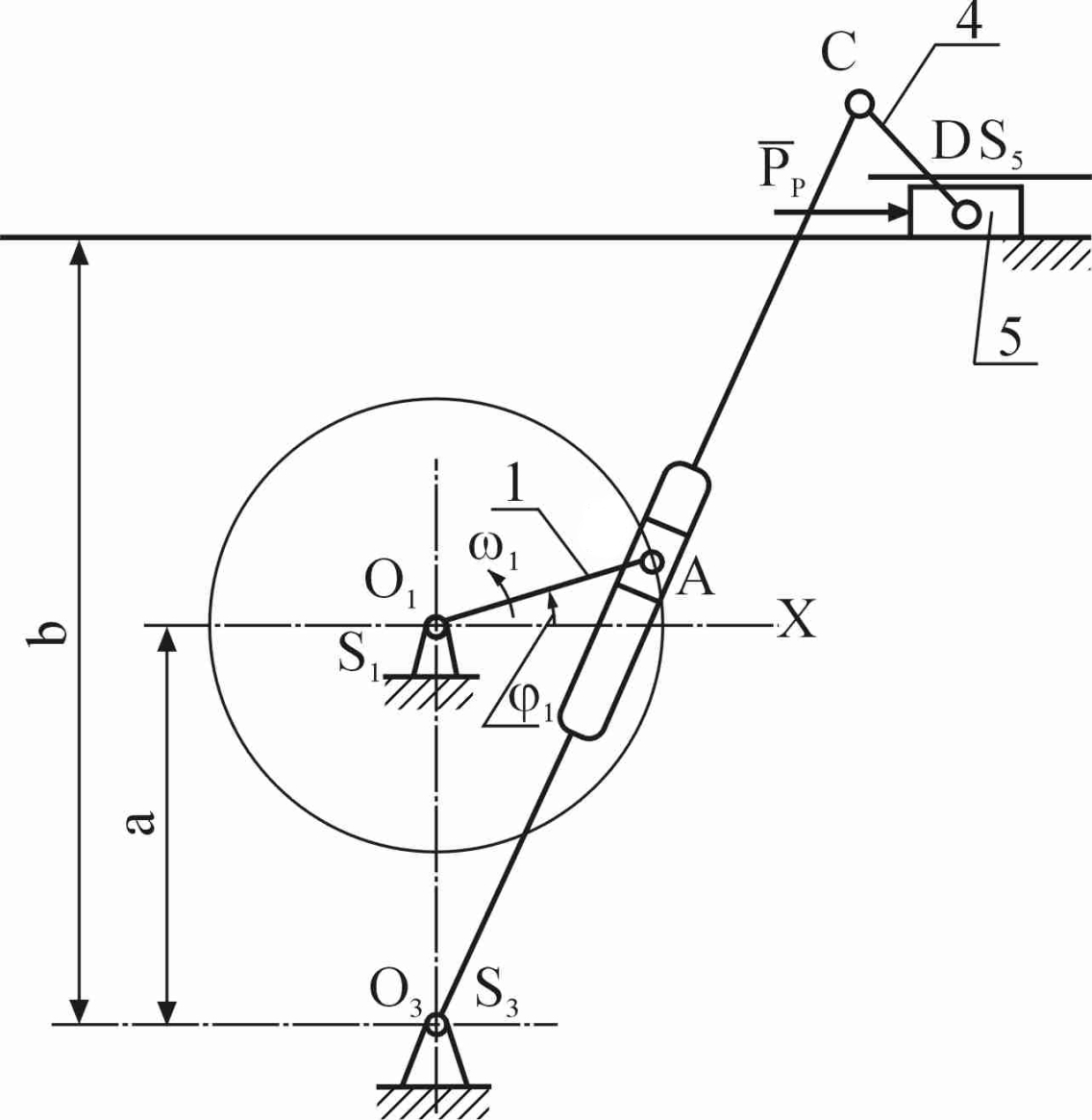
Рис. 2.7. Схема механизма брикетировочного автомата



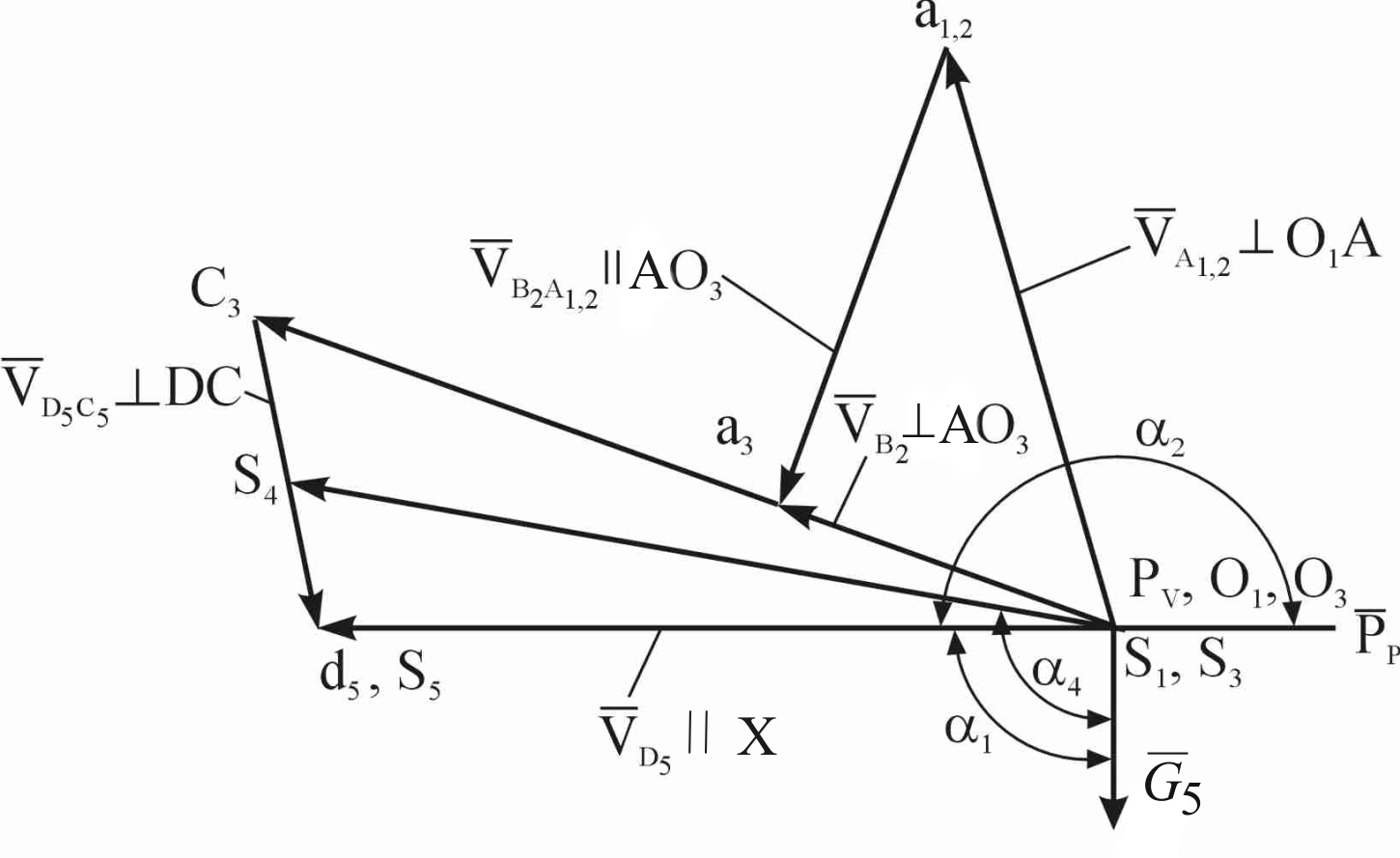
Рис. 2.8 План скоростей механизма брикетировочного автомата

Запишем уравнения

; .



Здесь – скорость неподвижной точки, равная нулю; – скорость точки A₃ относительно О₃; – скорость точки A_1,2 в относительном движении по отношению к А₃.



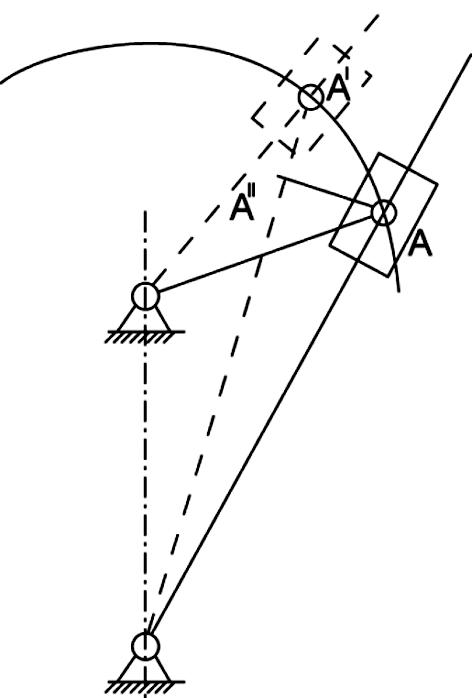
Рис.2.9. Сложение движений

Векторные уравнения решаем графически (рис. 2.8) Через полюс проводим направление перпендикулярно AО₃, а через конец вектора проводим прямую, параллельную AО₃. Пересечение определяет положение точки a₃

---

– конец вектора . Скорость точки С можно определить, используя свойство пропорциональности одноименных отрезков,

а именно: .

Откладываем на продолжение отрезок и находим точку .

Для скорости точки D векторное уравнение имеет вид

;

|| X

Решаем это уравнение графически (рис. 2.8). Через полюс р_v проводим направление скорости параллельно оси Х. Через точку c₃ проводим направление относительной скорости . Пересечение этих прямых дает точку d, с которой будет совпадать точка s₅, а точка s₄ по свойству пропорциональности лежит на середине вектора относительной скорости . Точки, скорость которых равна нулю, на плане скоростей находятся в полюсе .

Определяем величины линейных скоростей точек звеньев механизма:

= ∙μ_v = 26∙0,005 = 0,13 м/с;

= μ_v =36∙0,005 = 0,18 м/с;

= ∙μ_v

---