Файл: Учебное пособие для студентов очной и заочной форм обучения Рекомендовано учебнометодическим объединением вузов рф по образованию в области транспортных машин и транспортнотехнологических.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 208
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= 87 мм, т.е.  = 0,1 (м/с2 )/ мм.
= 0,1 (м/с2 )/ мм.
Из произвольно выбранной точки на чертеже (π – полюс плана) откладываем нормальную составляющую

 величиной 87 мм, направленную к центру вращения кривошипа 01 (рис.2.13). Конец вектора обозначим
величиной 87 мм, направленную к центру вращения кривошипа 01 (рис.2.13). Конец вектора обозначим  . Составляем векторные уравнения для определения ускорений других точек. Ускорения точки А, принадлежащей первому и второму звену (камню) будут равны
. Составляем векторные уравнения для определения ускорений других точек. Ускорения точки А, принадлежащей первому и второму звену (камню) будут равны 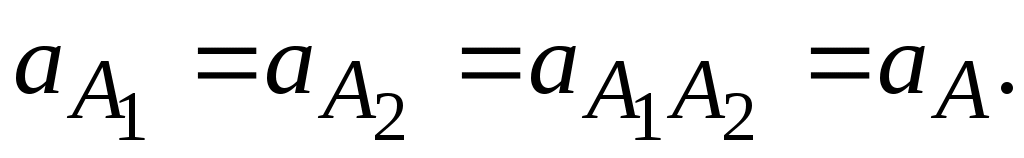
Для определения ускорения точки В запишем векторные уравнения движения этой точки относительно 03 и относительно точки А. Имеем
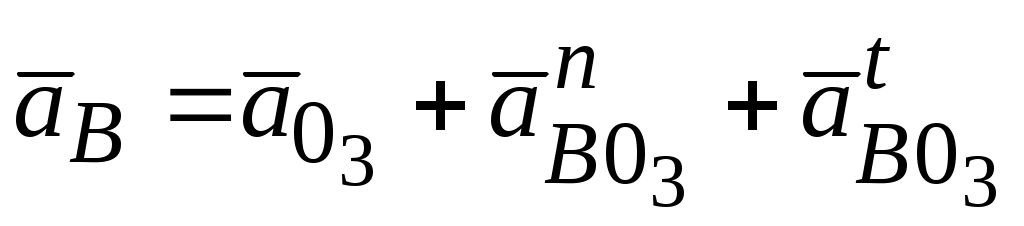 ;
; 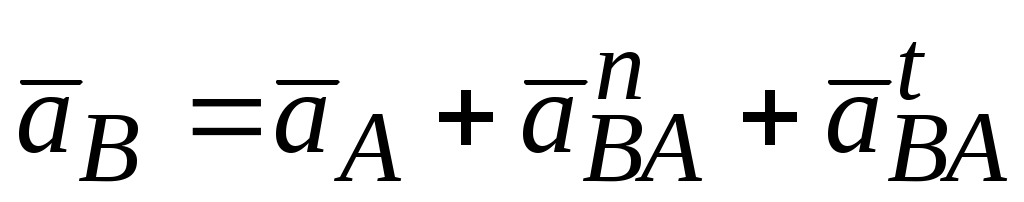 .
.
Используя план скоростей (рис.2.10), вычисляем составляющие:
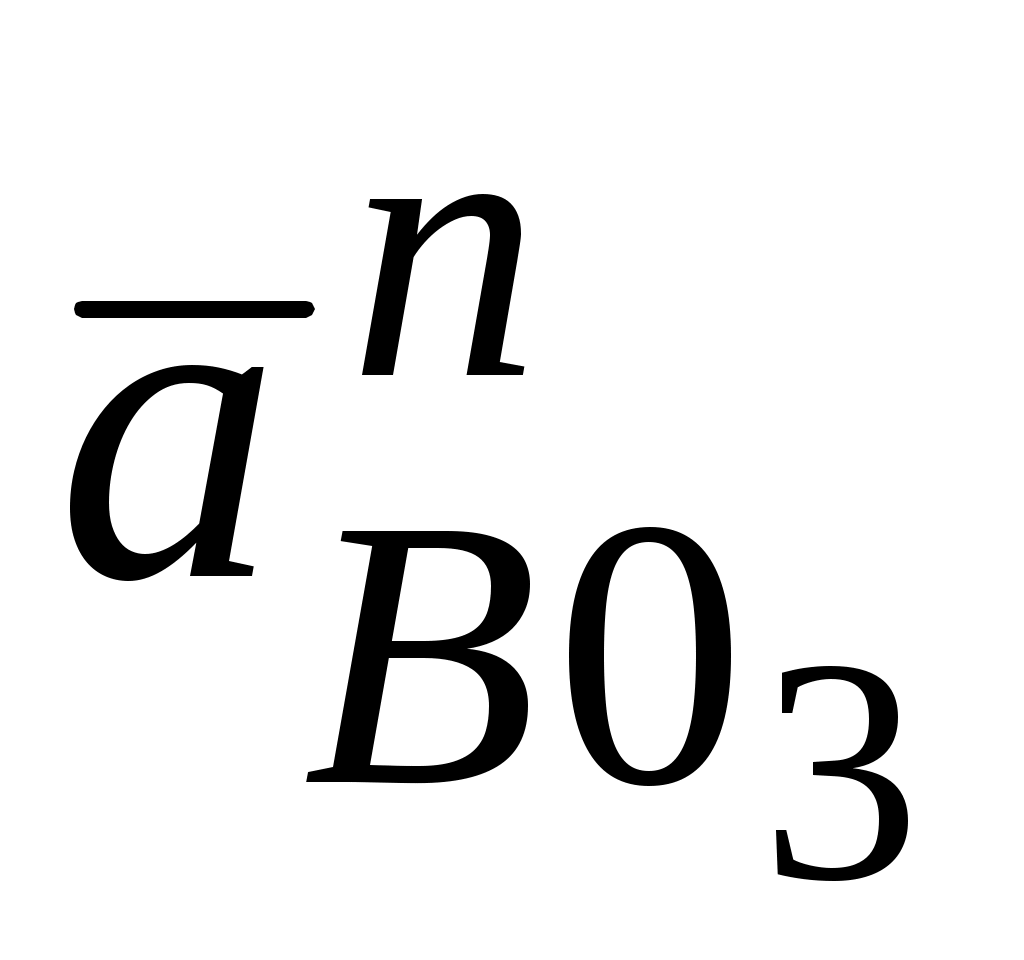 =
= 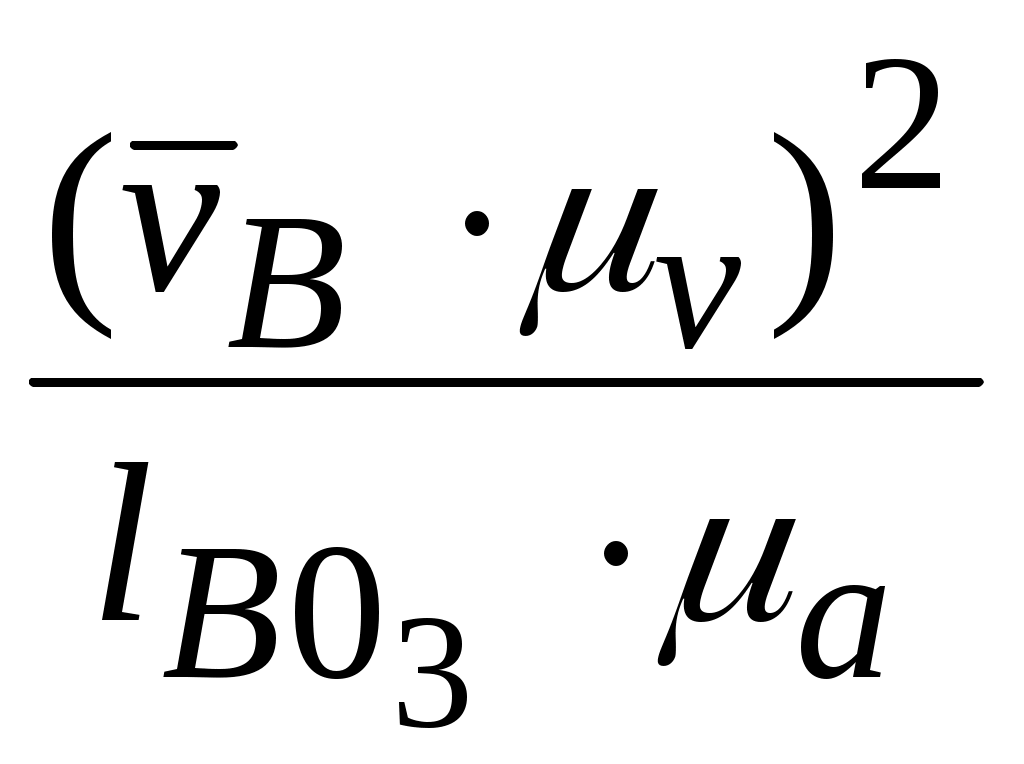 мм, или
мм, или 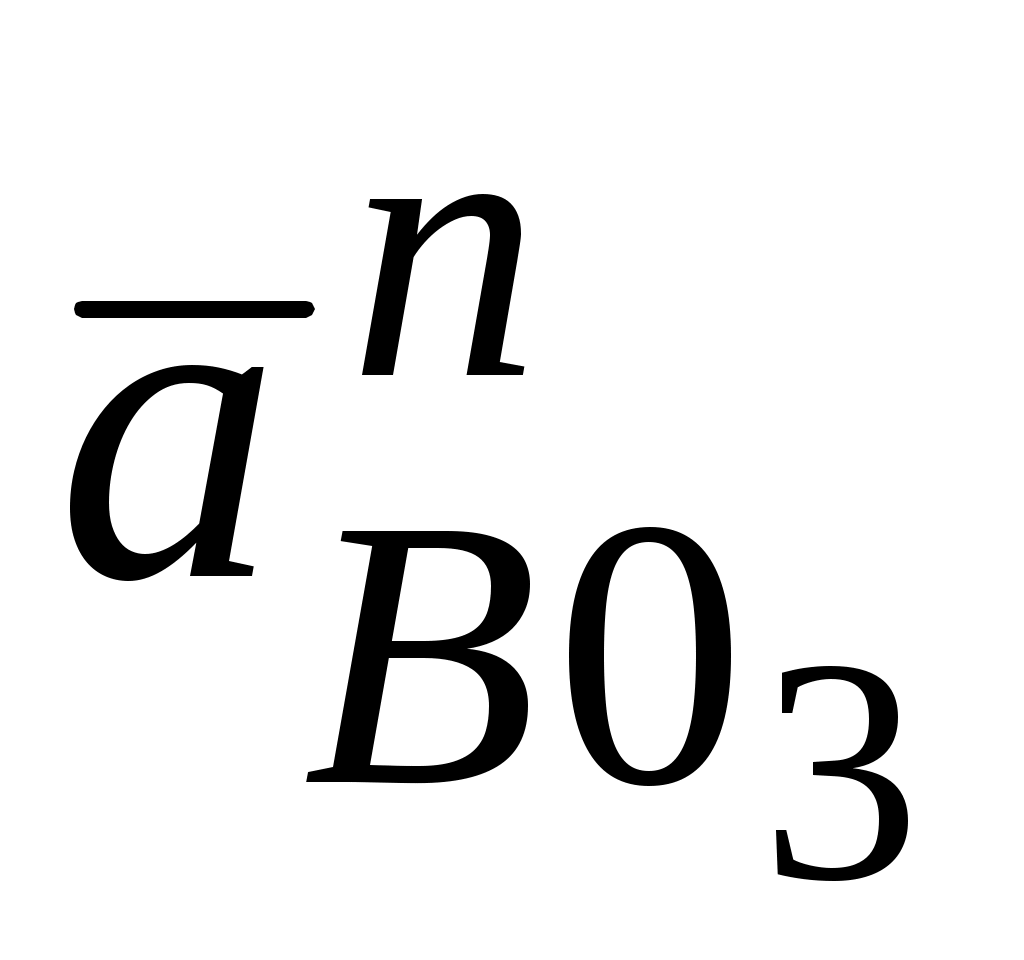 =
= 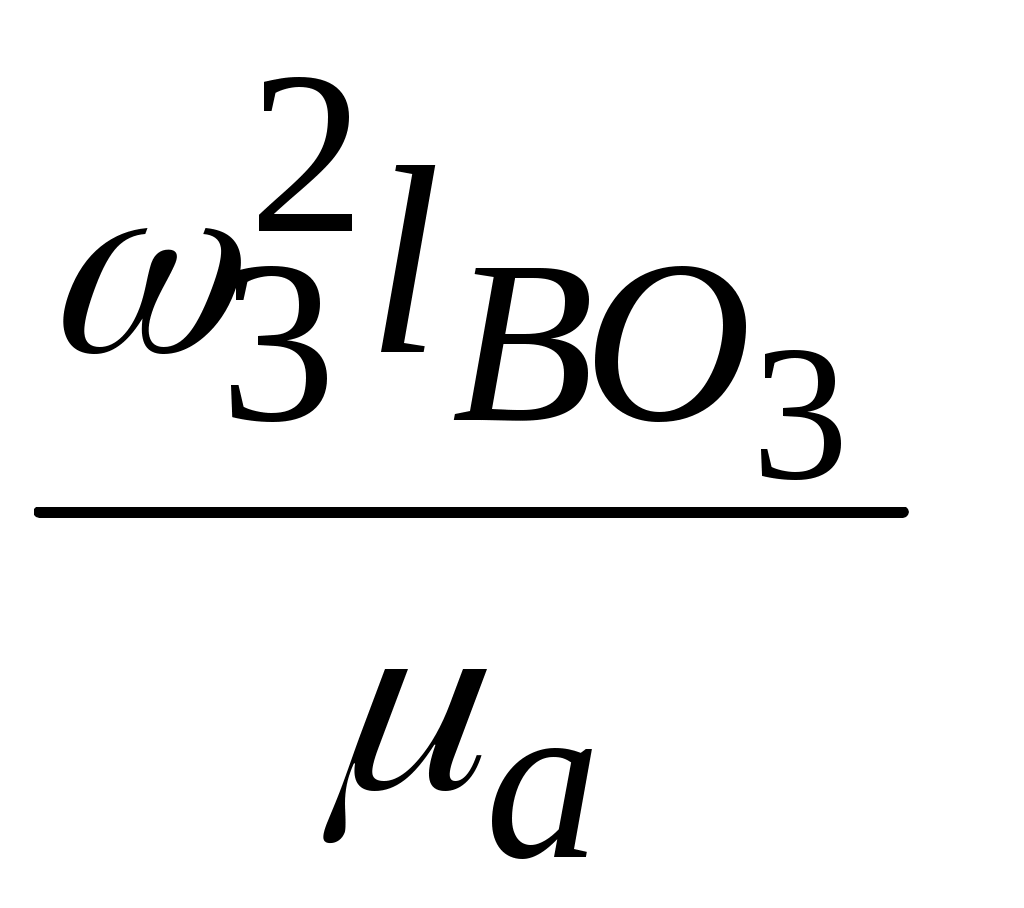 мм. Аналогично
мм. Аналогично 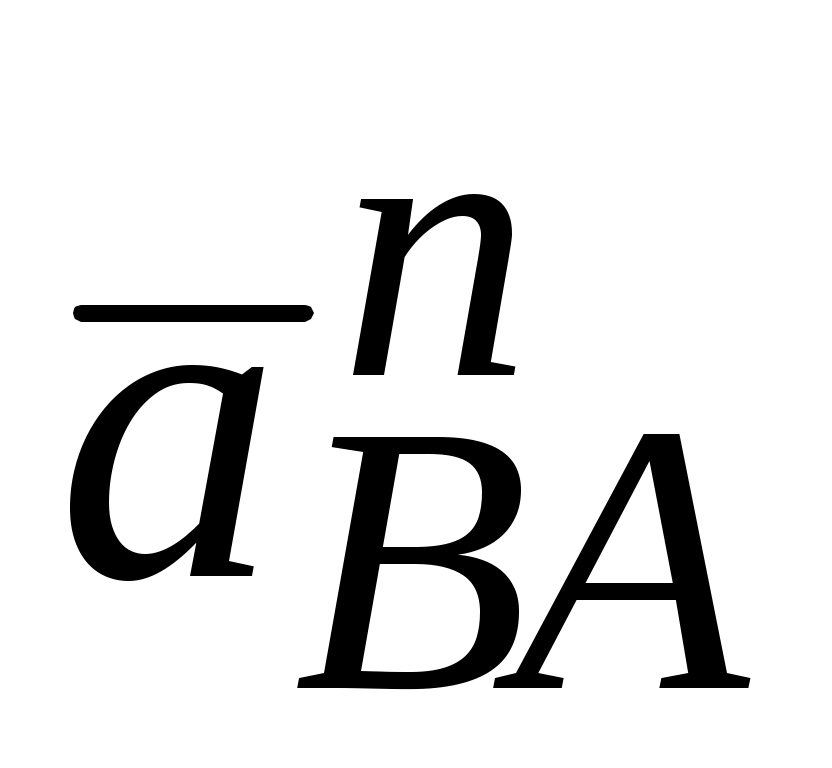 =
= 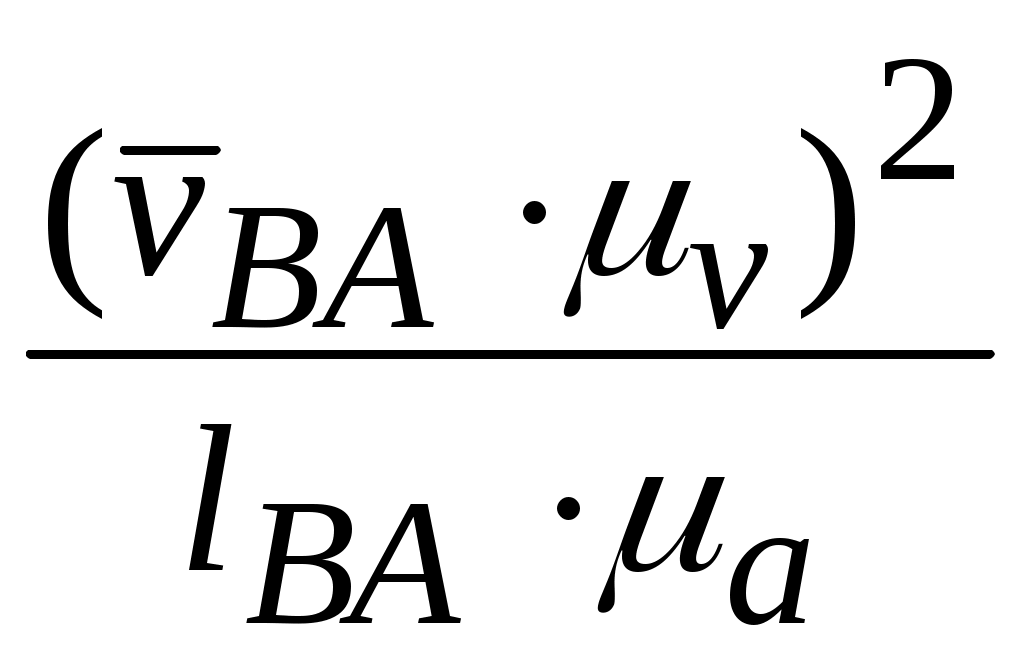 мм. Находим положение конца вектора
мм. Находим положение конца вектора  на плане ускорений. Из полюса π проводим вектор
на плане ускорений. Из полюса π проводим вектор 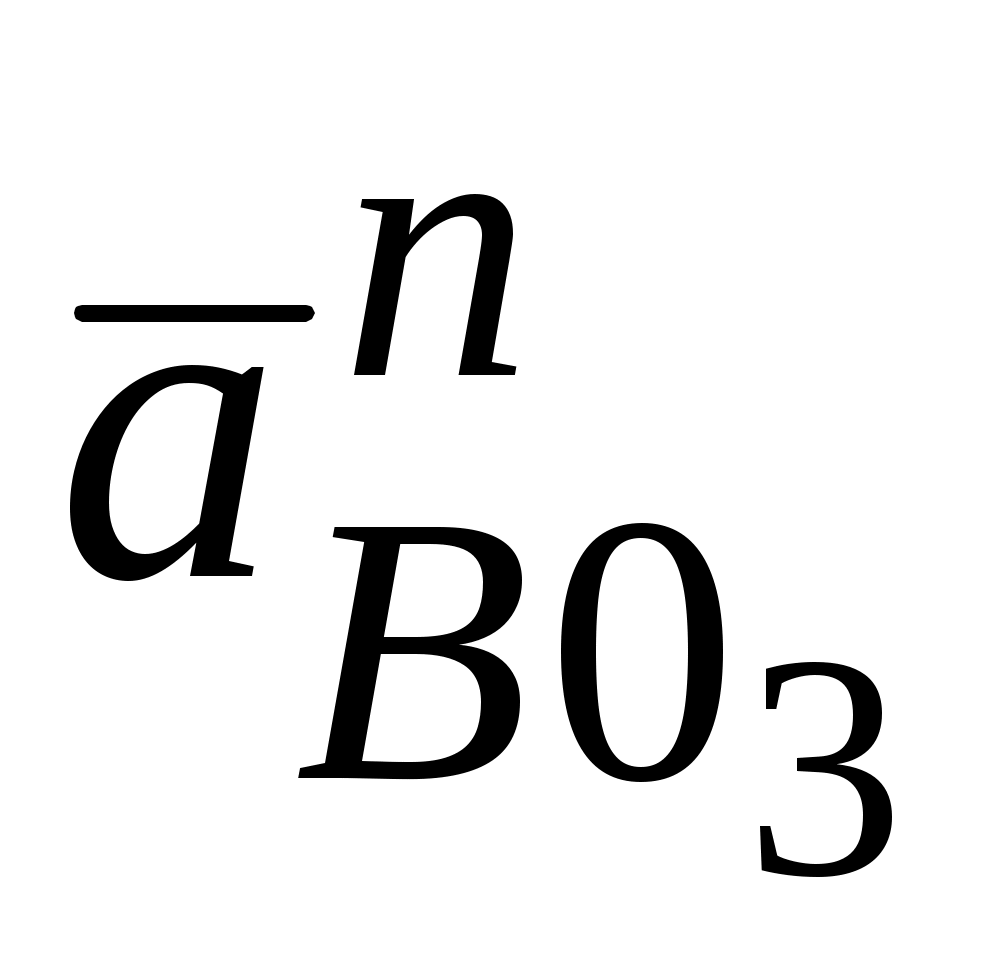 || О3В (конец вектора обозначаем n1) и через него направление вектора
|| О3В (конец вектора обозначаем n1) и через него направление вектора 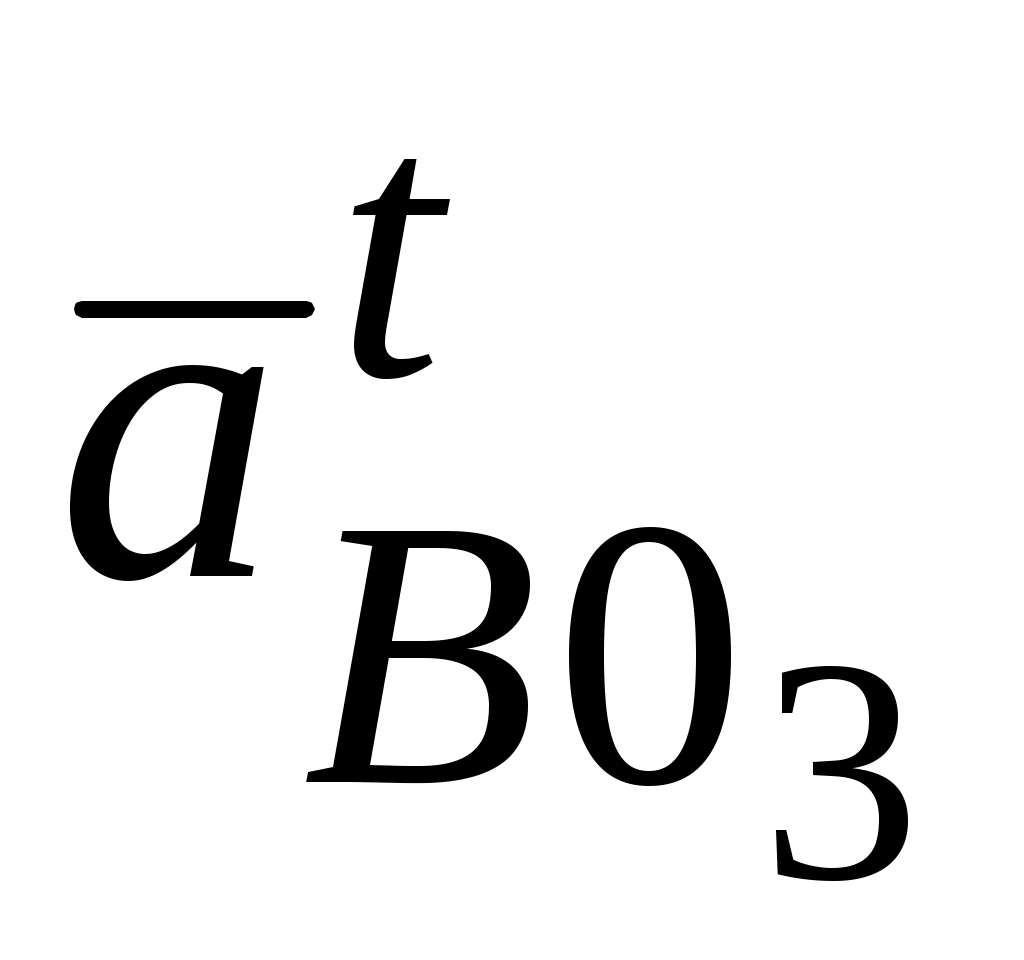
 О3В. Далее из конца вектора
О3В. Далее из конца вектора 
строим вектор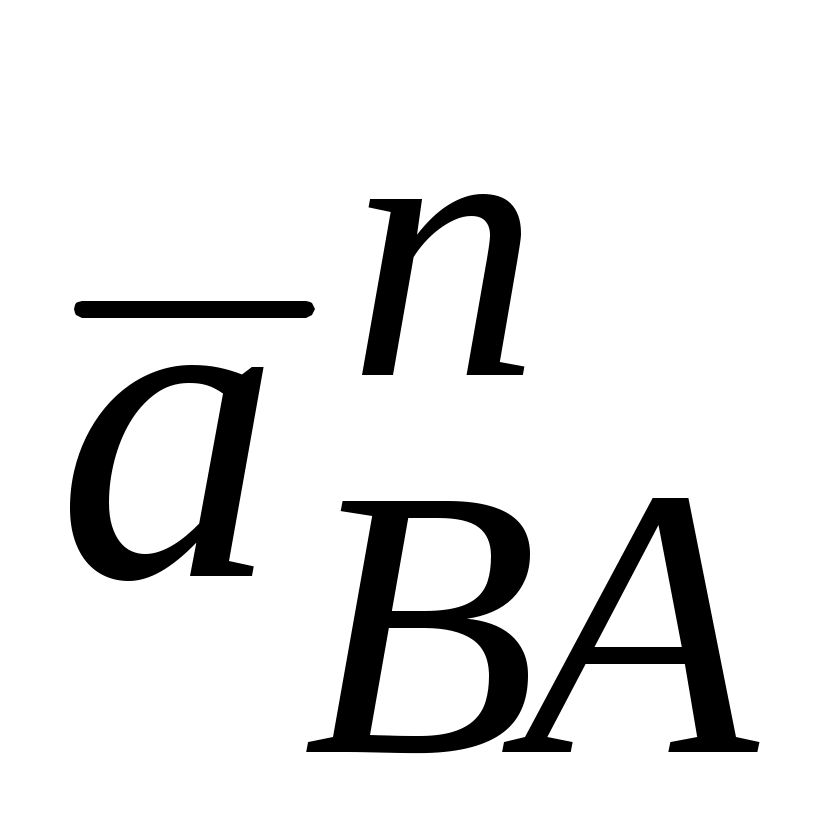 ||АВ (конец вектора
||АВ (конец вектора 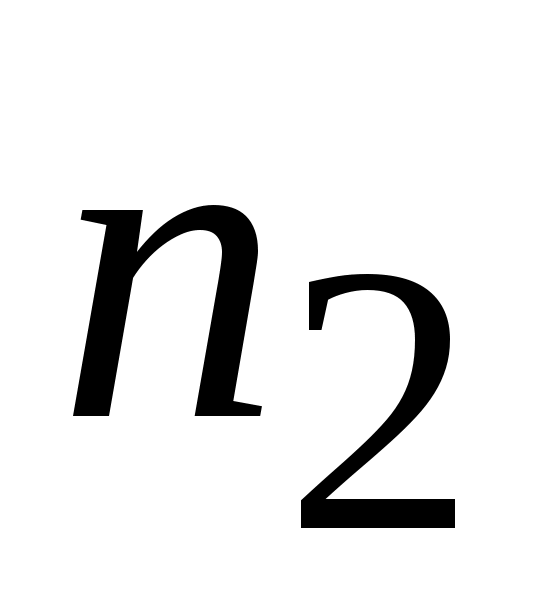 ) и через его конец проводим направление вектора
) и через его конец проводим направление вектора 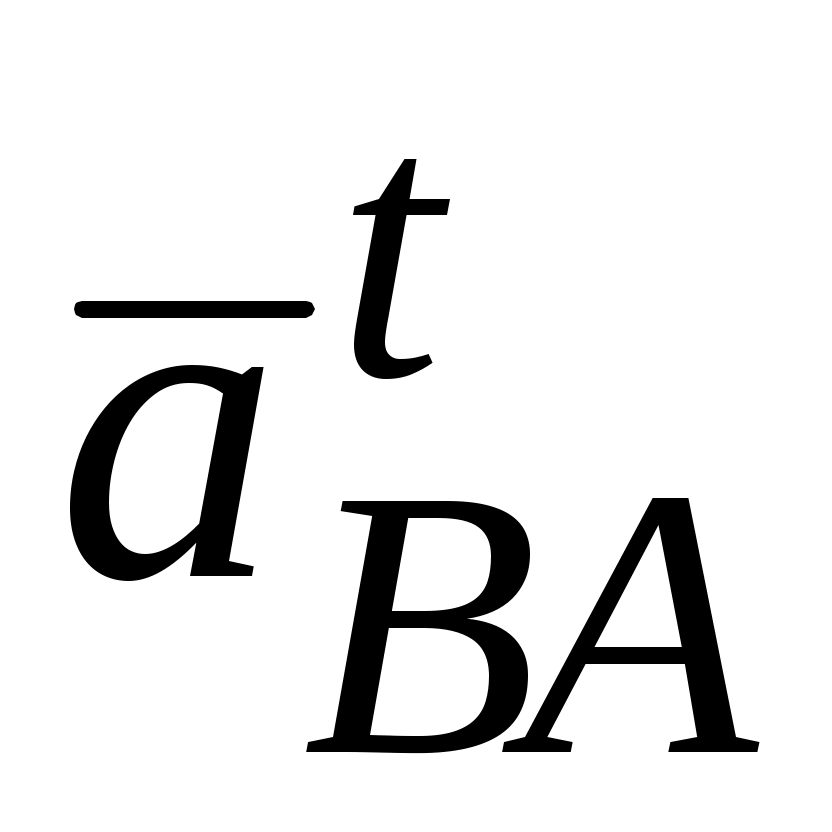
 ВА до пересечения с направлением вектора
ВА до пересечения с направлением вектора  . Точка пересечения и будет точка
. Точка пересечения и будет точка  конец вектора
конец вектора 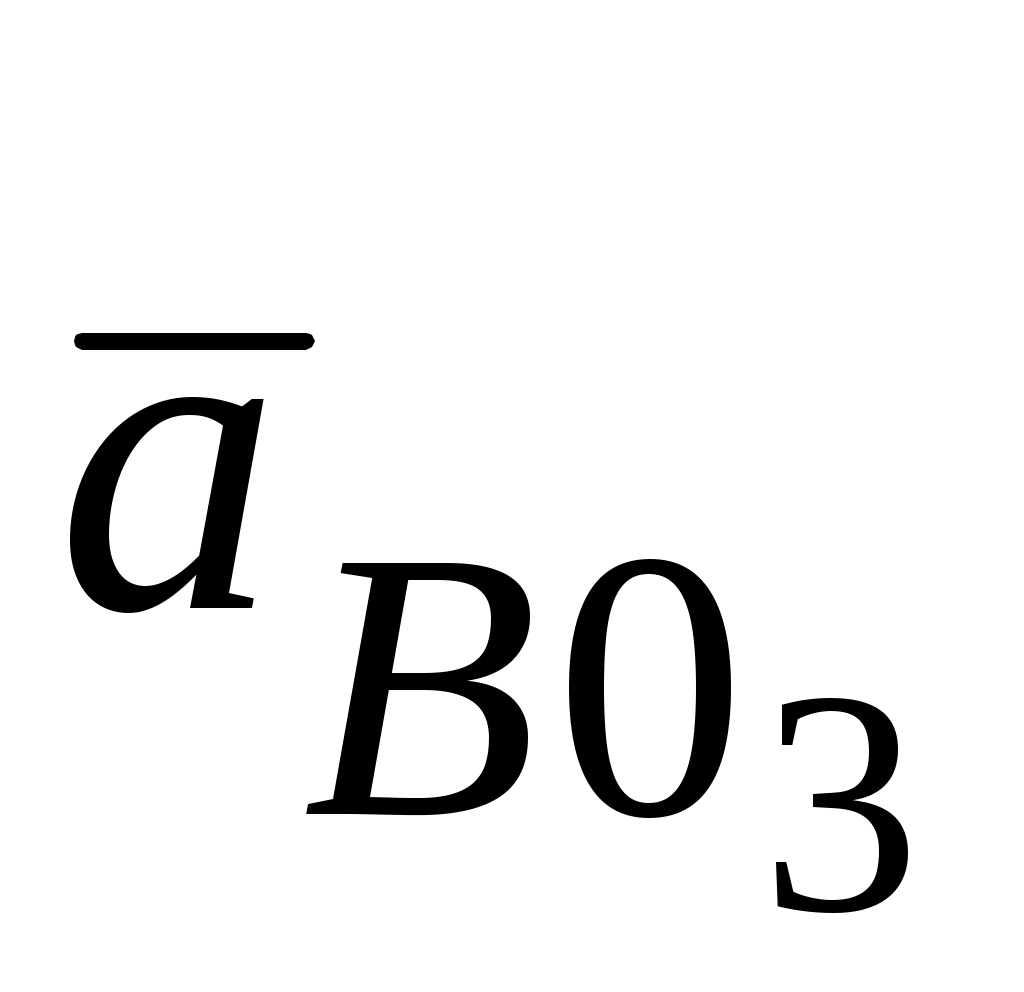 =
=  +
+ . Вектор
. Вектор 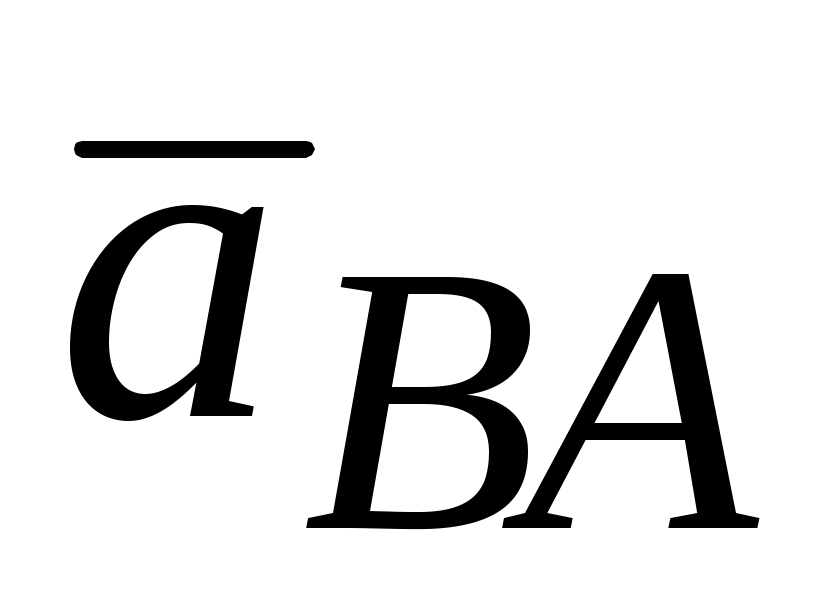 =
=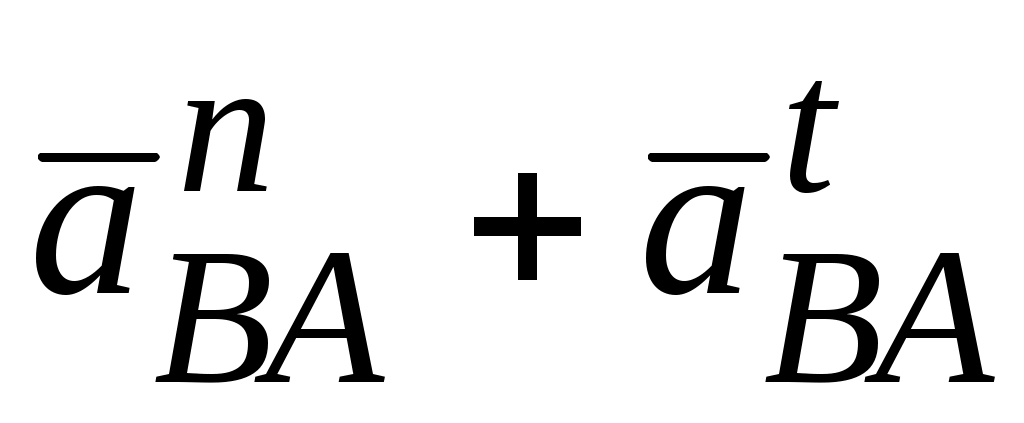 избражен отрезком на плане ускорений
избражен отрезком на плане ускорений 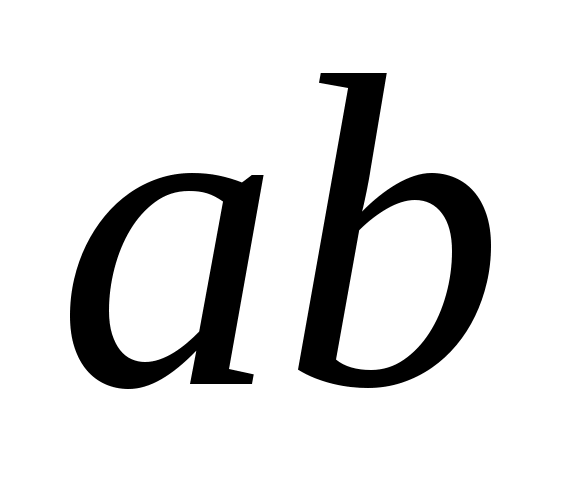 , в середине которого располагается точка
, в середине которого располагается точка 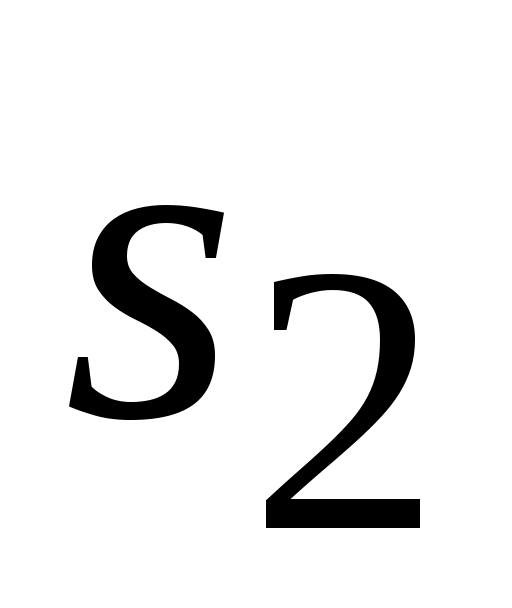 , конец вектора укорения центра масс шатуна. Положение точки
, конец вектора укорения центра масс шатуна. Положение точки 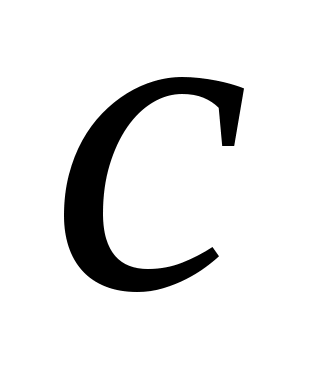 находим, используя свойство подобия. Треугольник ВО3С на плане положений механизма должен быть подобен и сходственно расположен соответствующему треугольнику на плане ускорений
находим, используя свойство подобия. Треугольник ВО3С на плане положений механизма должен быть подобен и сходственно расположен соответствующему треугольнику на плане ускорений 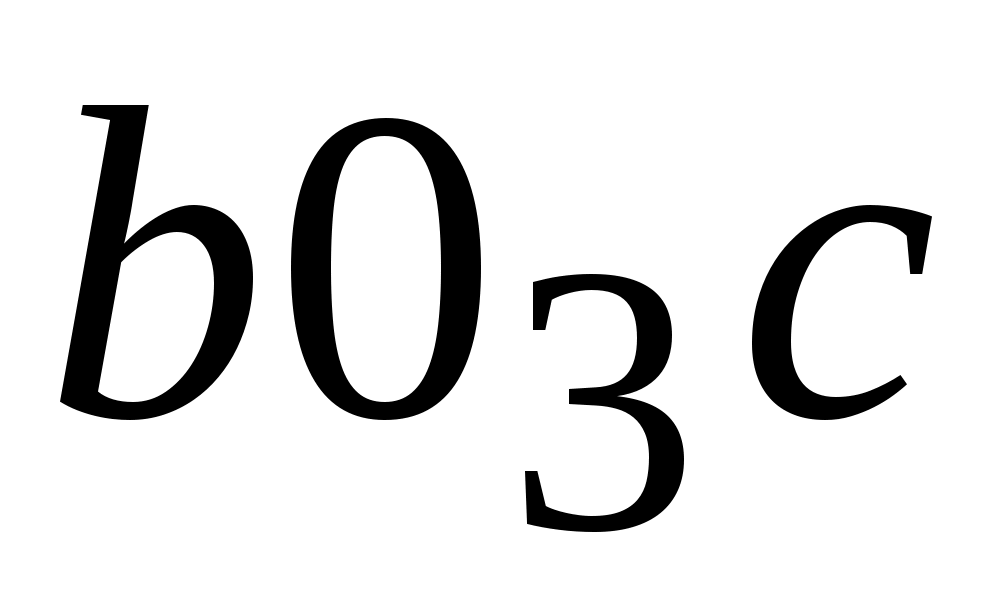 .
.
Запишем векторные ускорения для определения ускорения точки D, имеем
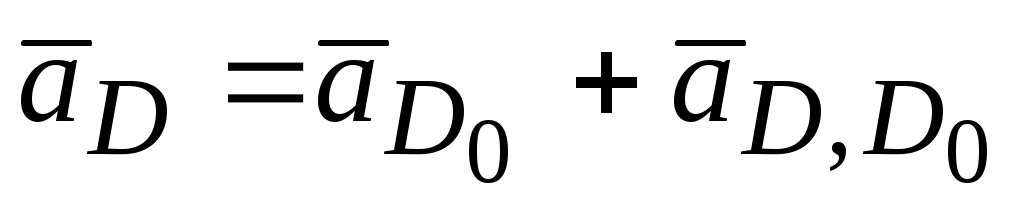 и
и 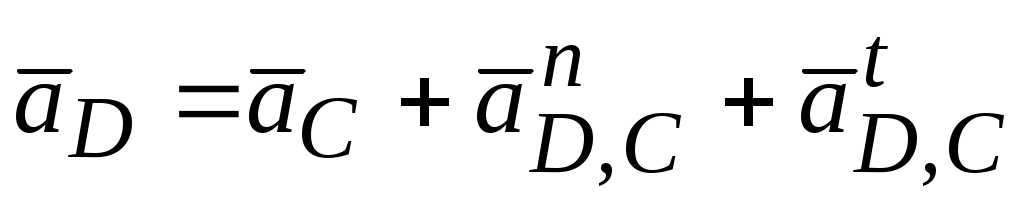 . Величина вектора
. Величина вектора 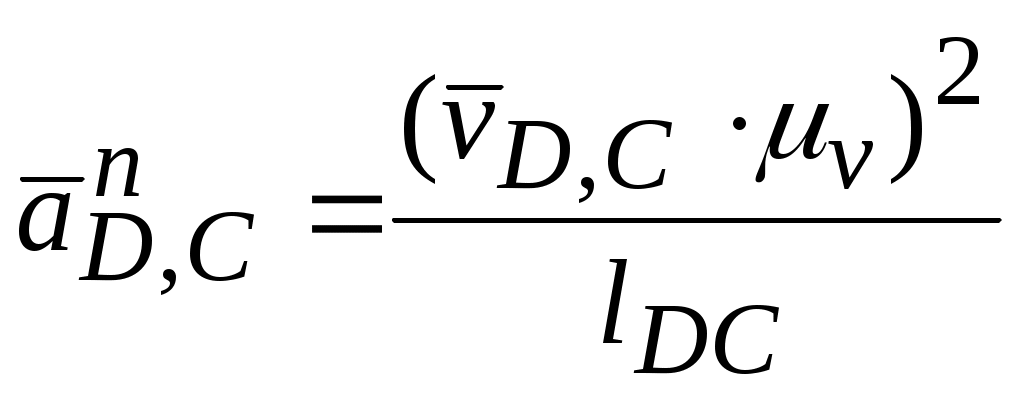 мм.
мм. 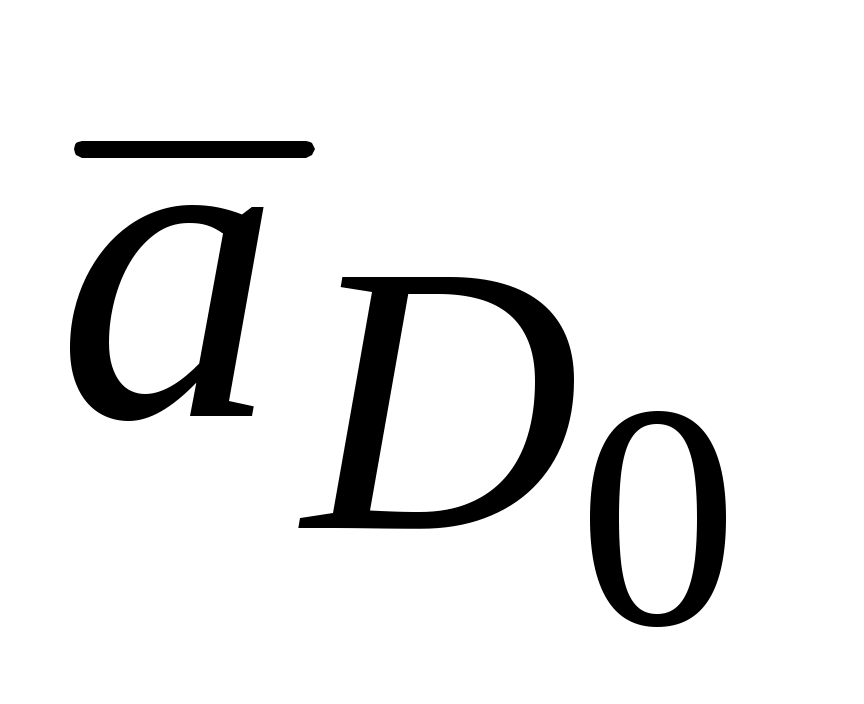 = 0, а вектор
= 0, а вектор 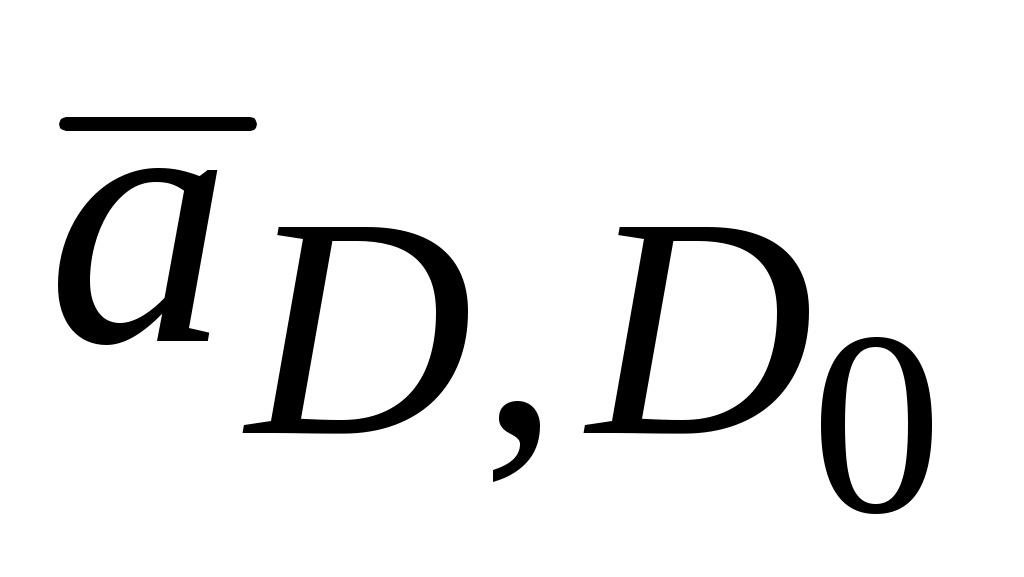 представляет ускорение вдоль направляющих, т.е. абсолютное ускорение точки D,
представляет ускорение вдоль направляющих, т.е. абсолютное ускорение точки D, 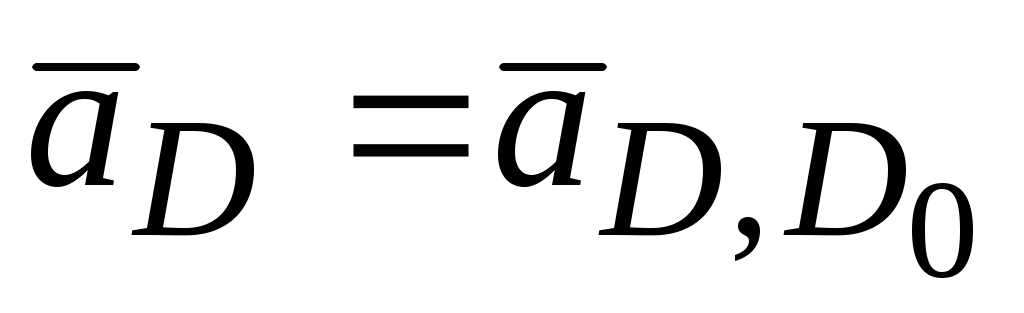
Проводим через полюс вертикальную прямую, направление вектора
вертикальную прямую, направление вектора  . Из конца вектора
. Из конца вектора 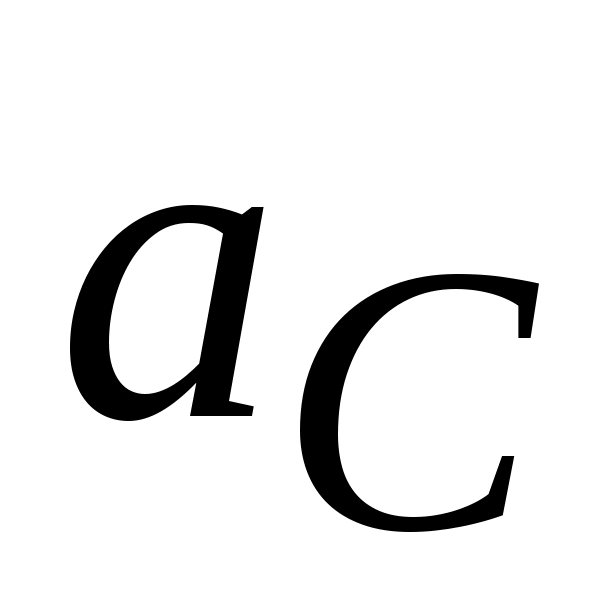 , точки
, точки  проводим величину вектора
проводим величину вектора 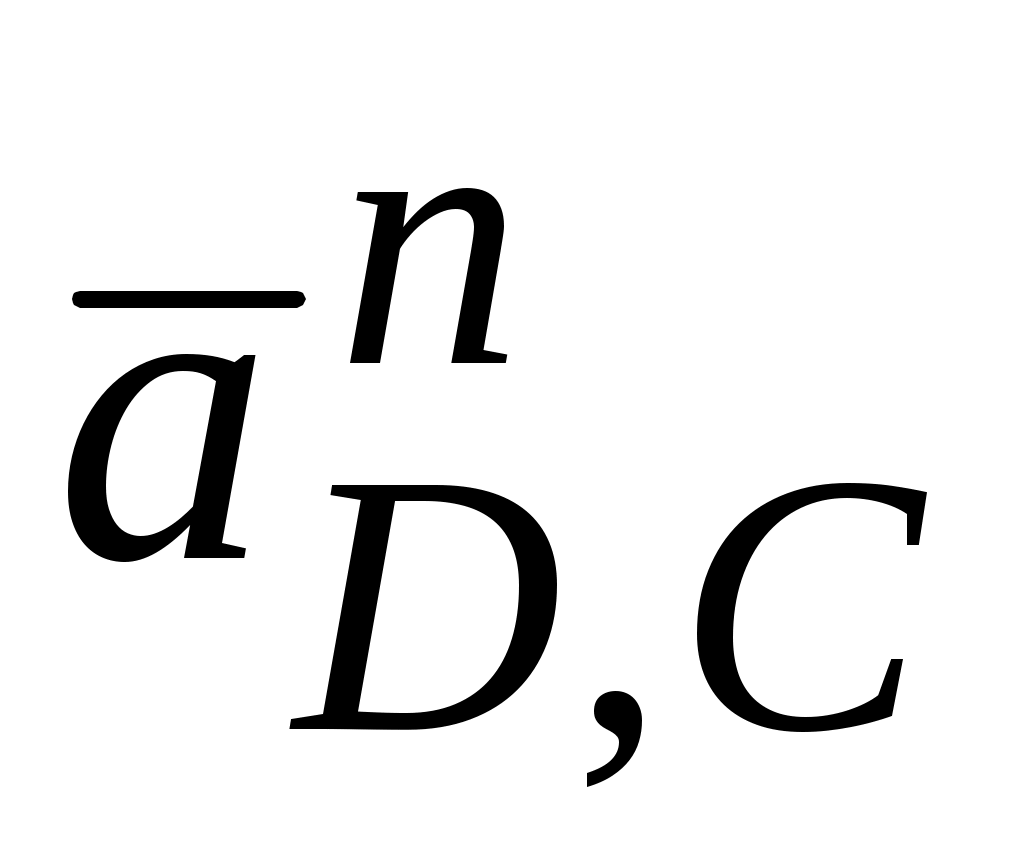 ||DC и из его конца (точка
||DC и из его конца (точка 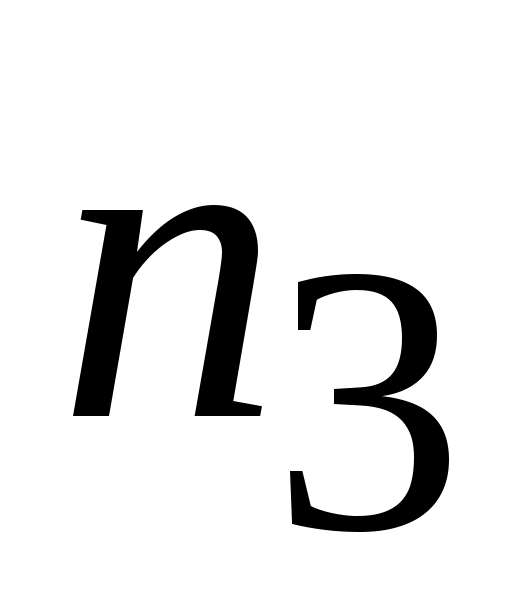 ) проводим
) проводим  DC прямую до пересечения с направлением вектора
DC прямую до пересечения с направлением вектора 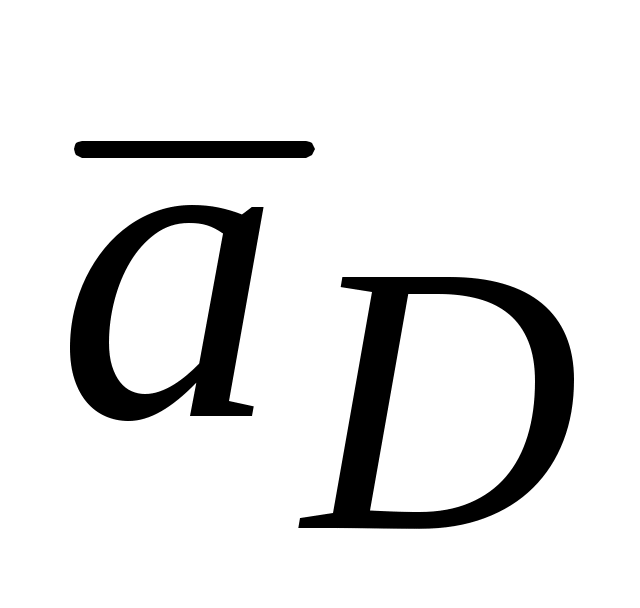 . Точка пересечения будет конец вектора
. Точка пересечения будет конец вектора 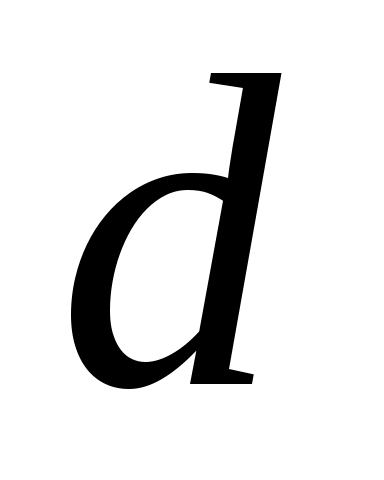 . Сумма векторов
. Сумма векторов 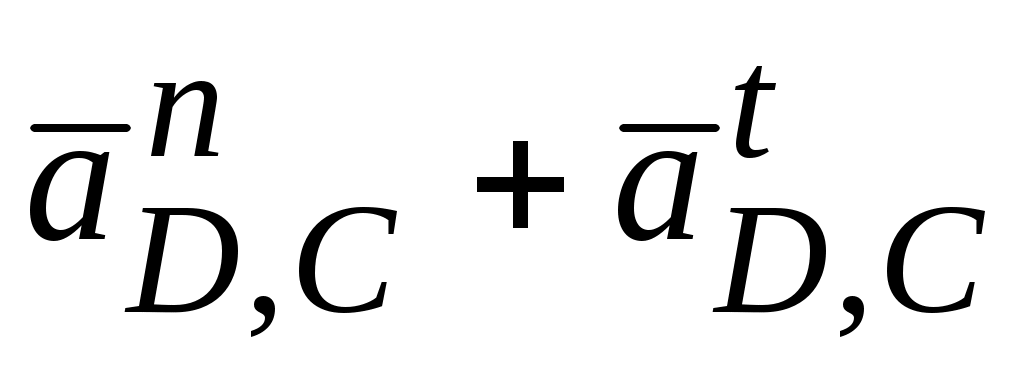 =
=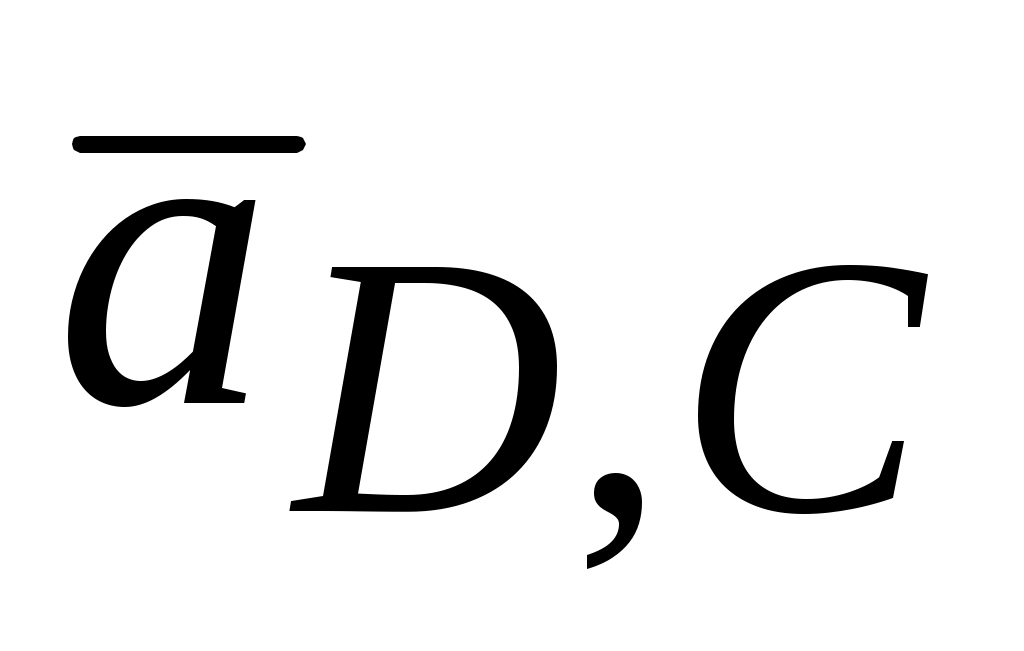 . Точка
. Точка 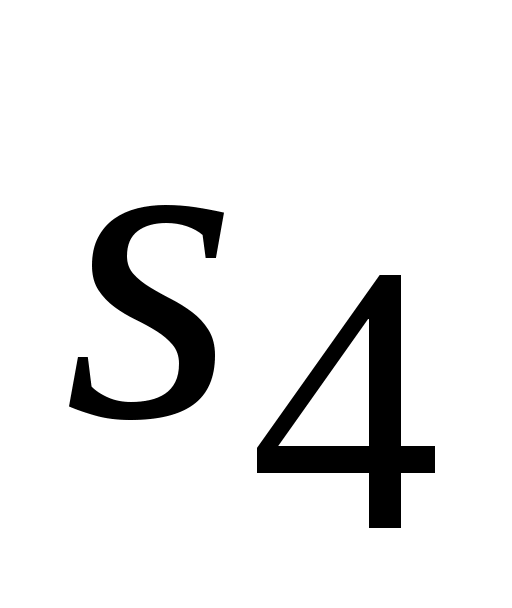 в силу свойства подобия будет лежать на середине отрезка
в силу свойства подобия будет лежать на середине отрезка 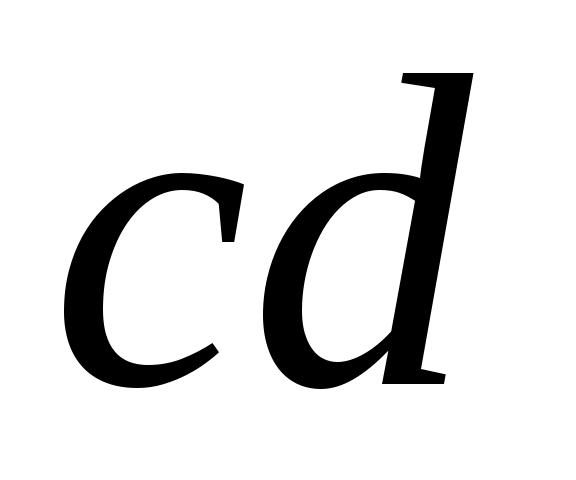 плана усорений. Соединив его с полюсом, получим вектор, отображающий ускорение центра масс шатуна
плана усорений. Соединив его с полюсом, получим вектор, отображающий ускорение центра масс шатуна 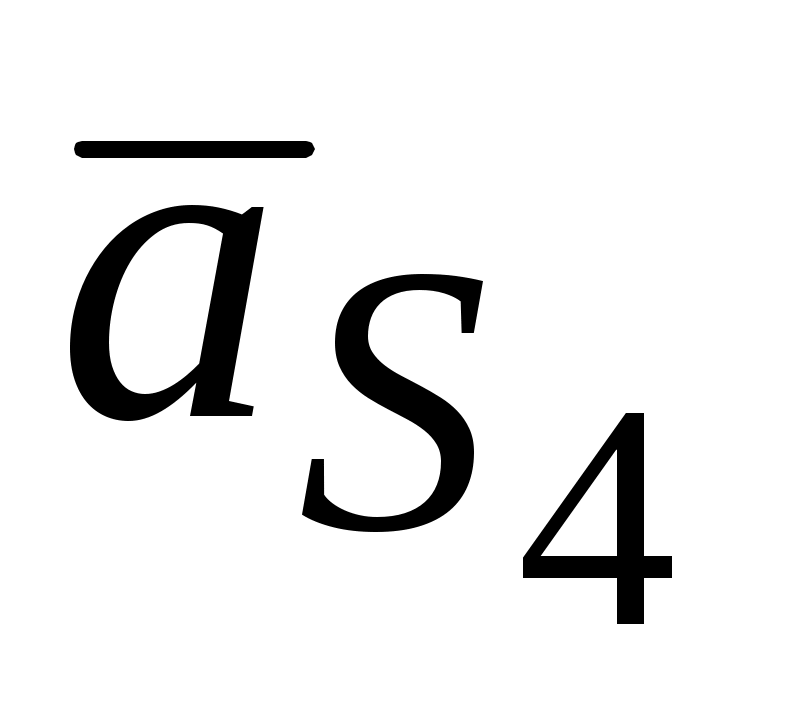 .
.
Определяем величины и направления линейных и угловых ускорений звеньев механизма.
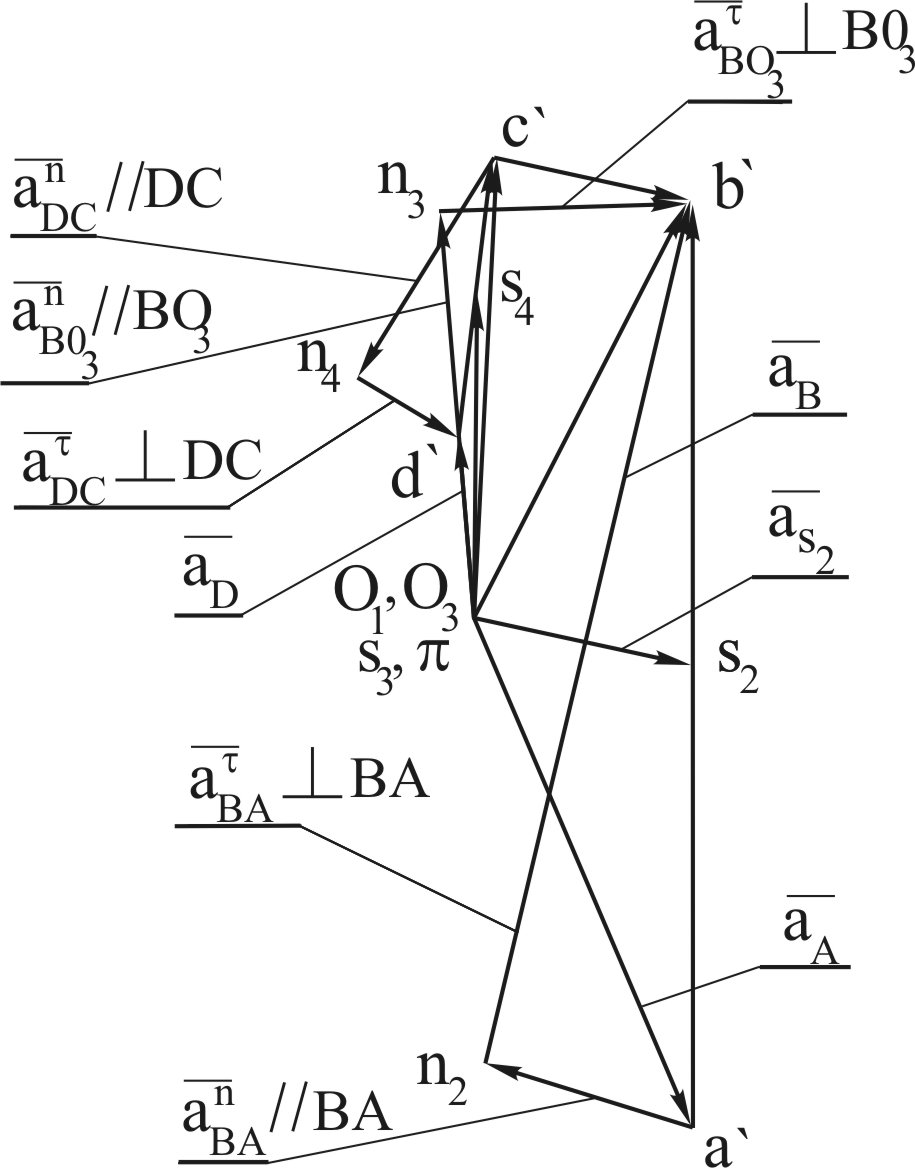
Рис.2.13. План ускорений механизма компрессора
Измеряем величины векторов в мм на плане ускорений и умножаем на масштабный коэффициент плана, получаем значения в м/с2. Итак имеем
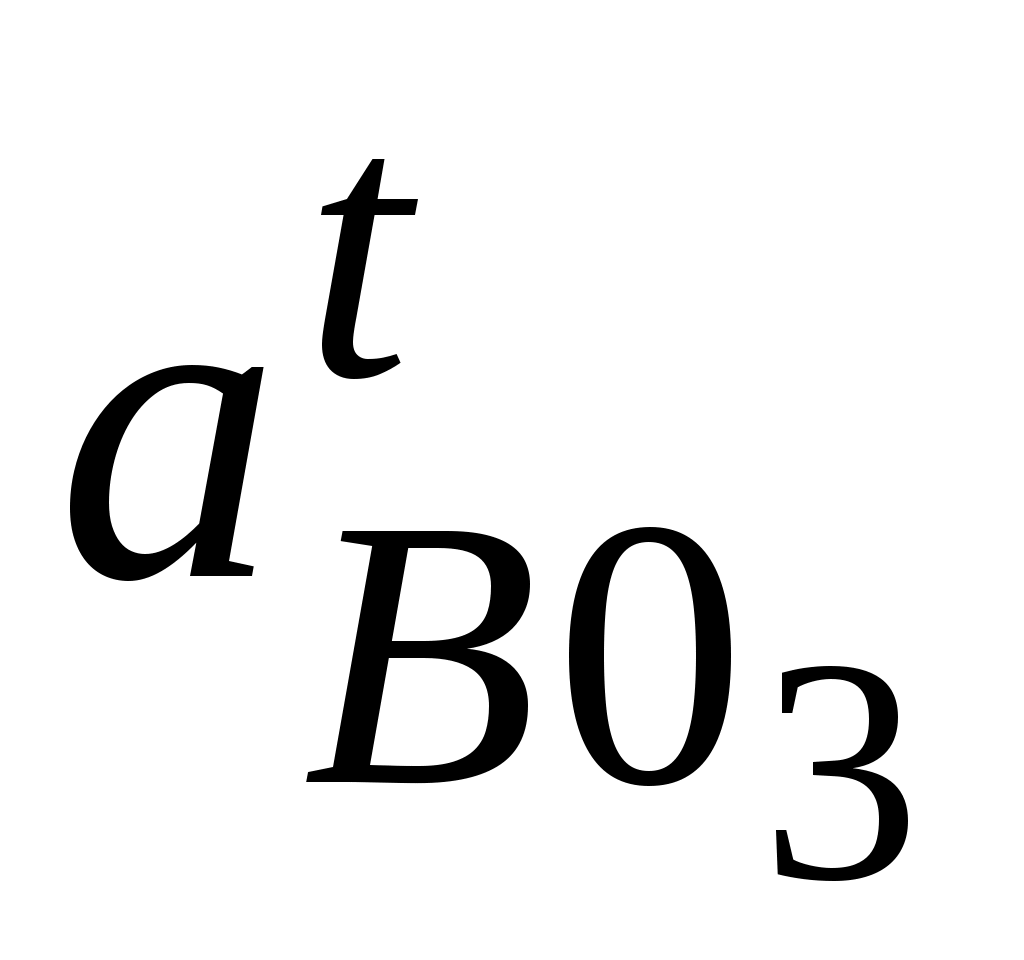 =
=  ·
·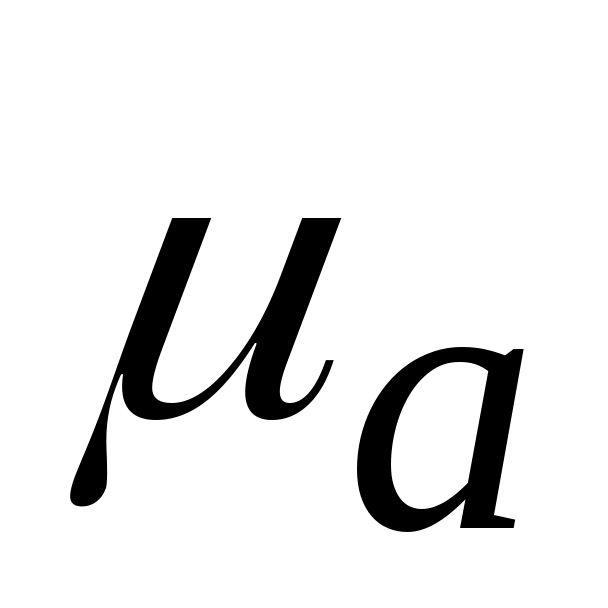 (м/с2);
(м/с2);
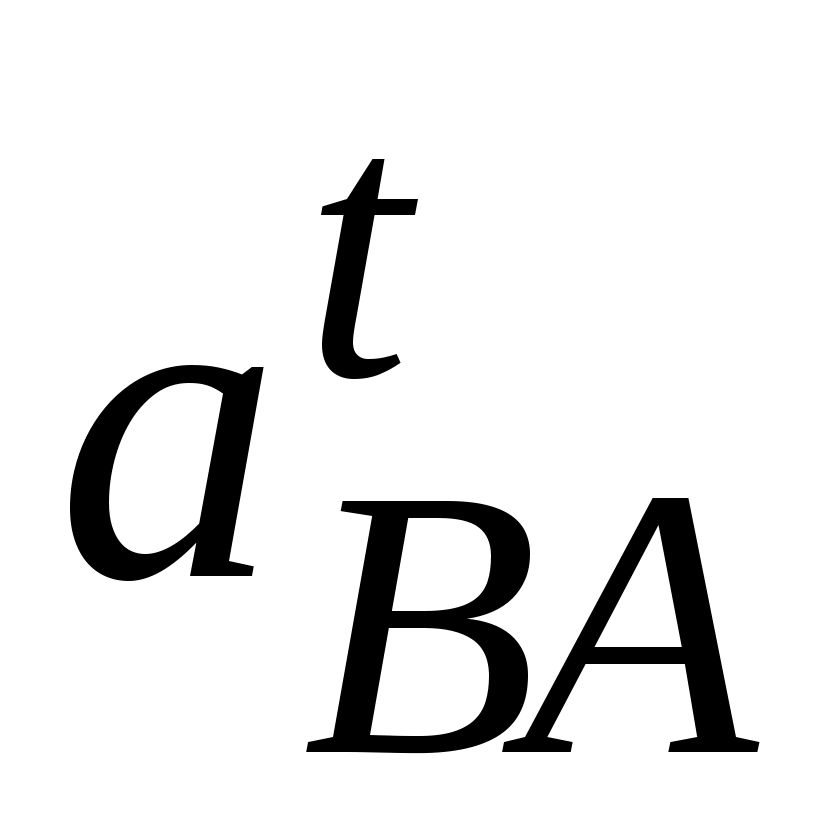 =
= ·
·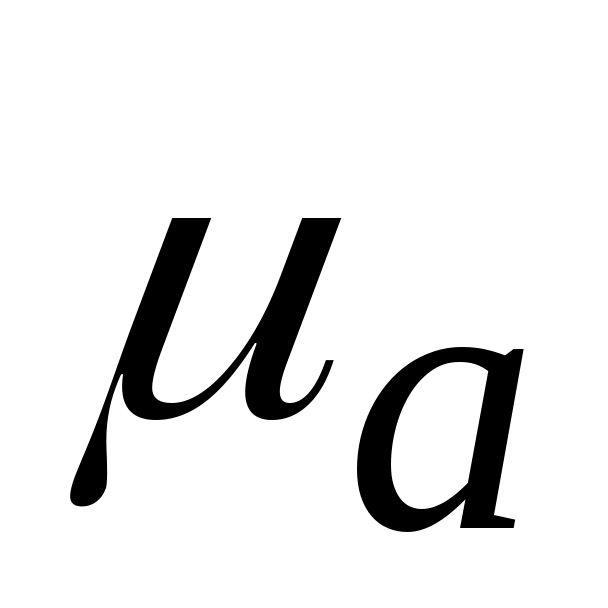
(м/с2);
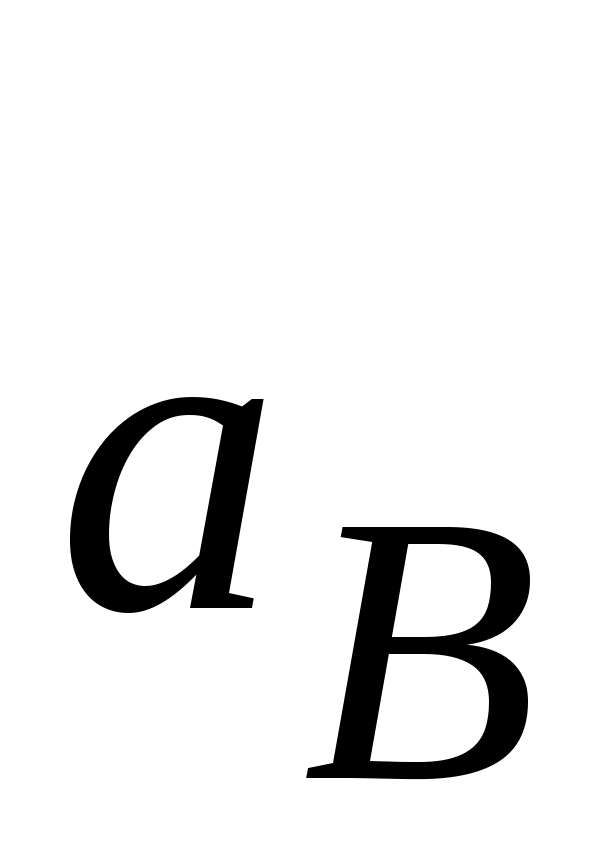 =
= 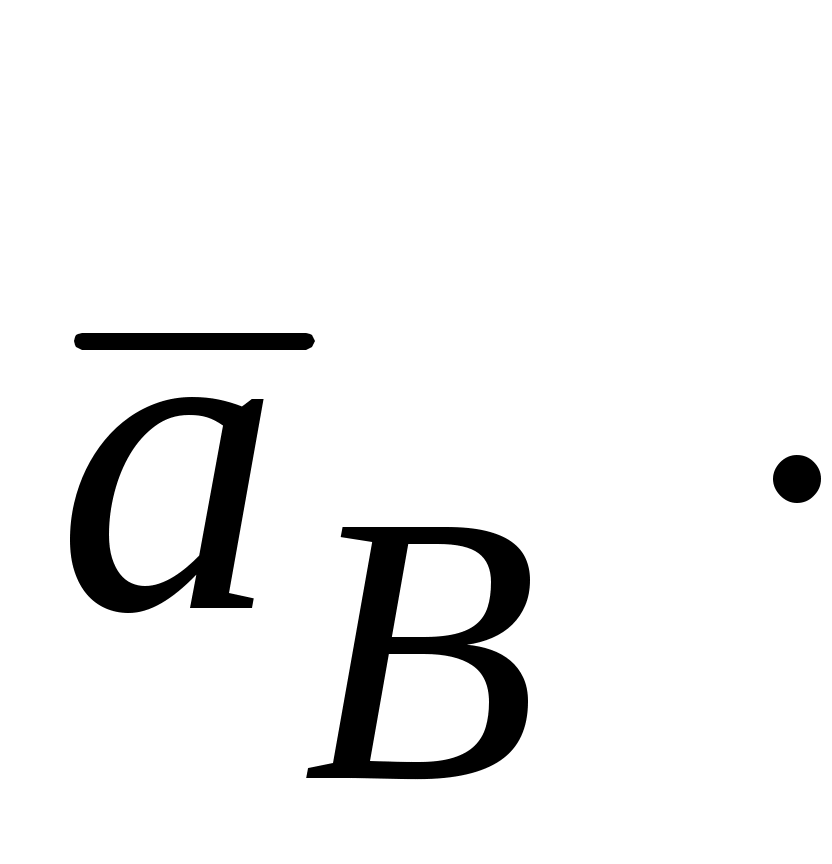
 (м/с2);
(м/с2);
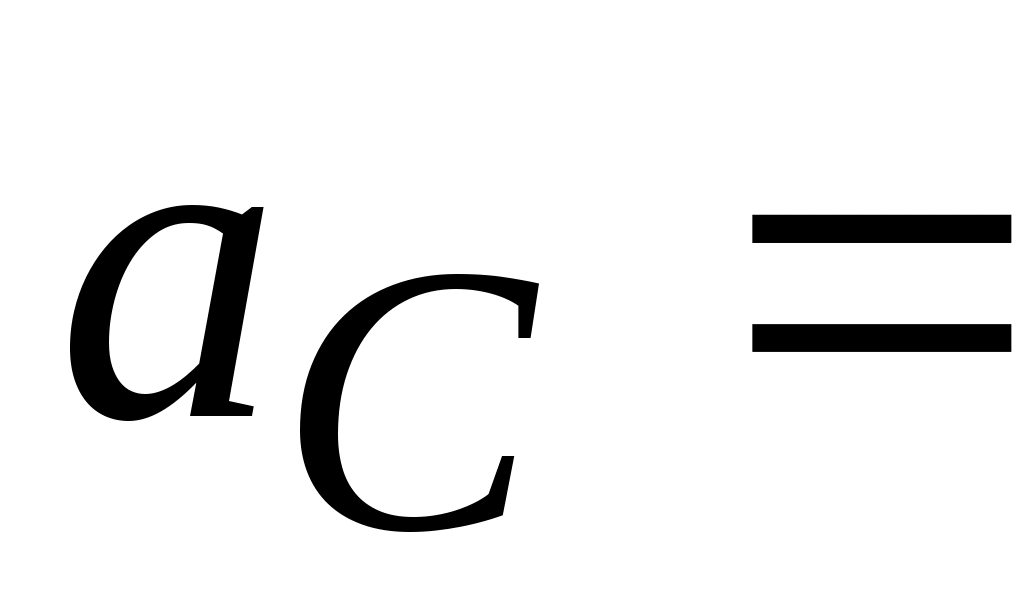
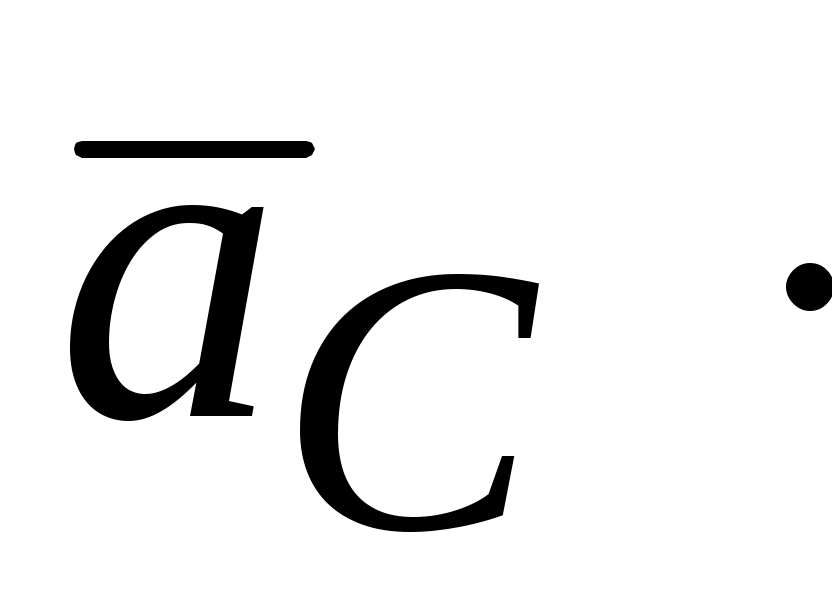
 (м/с2);
(м/с2);
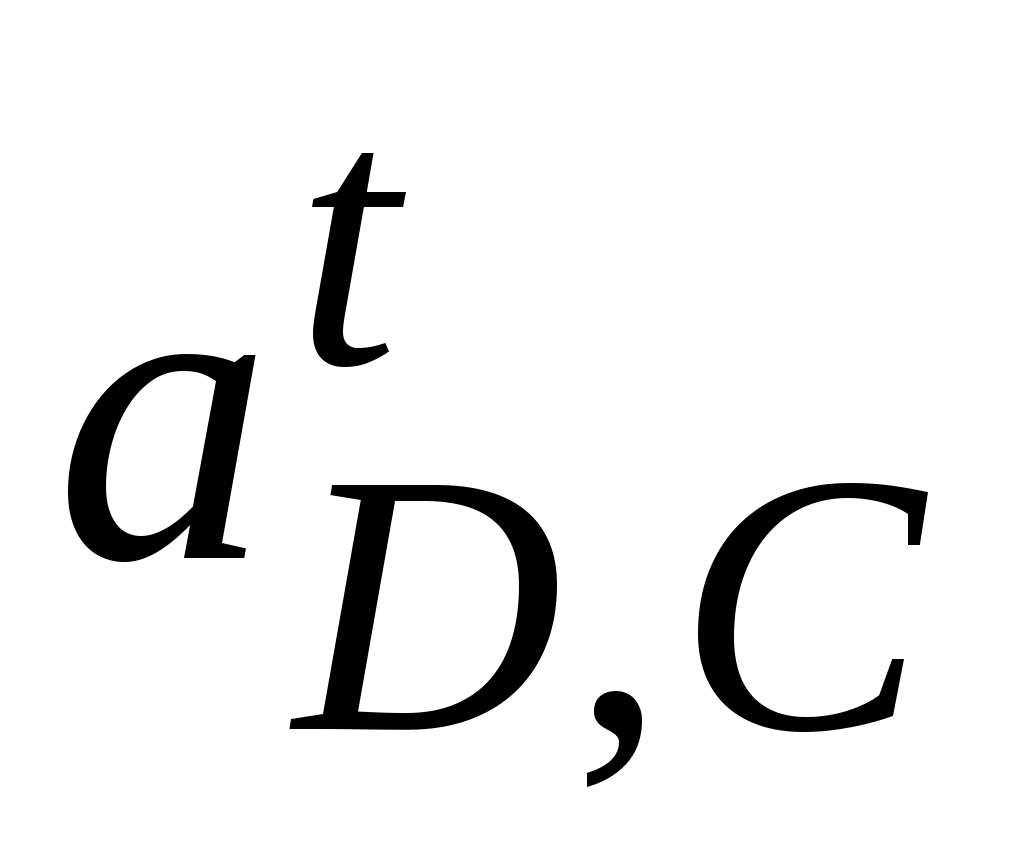 =
=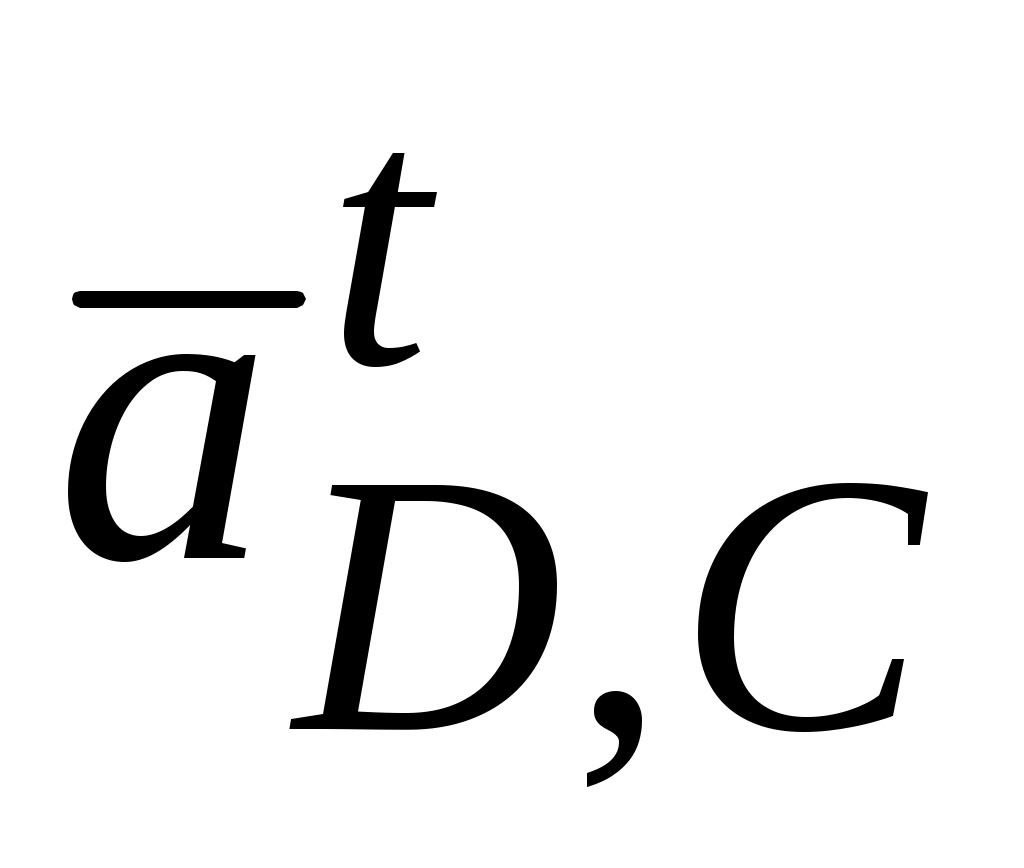 ·
· (м/с2);
(м/с2);
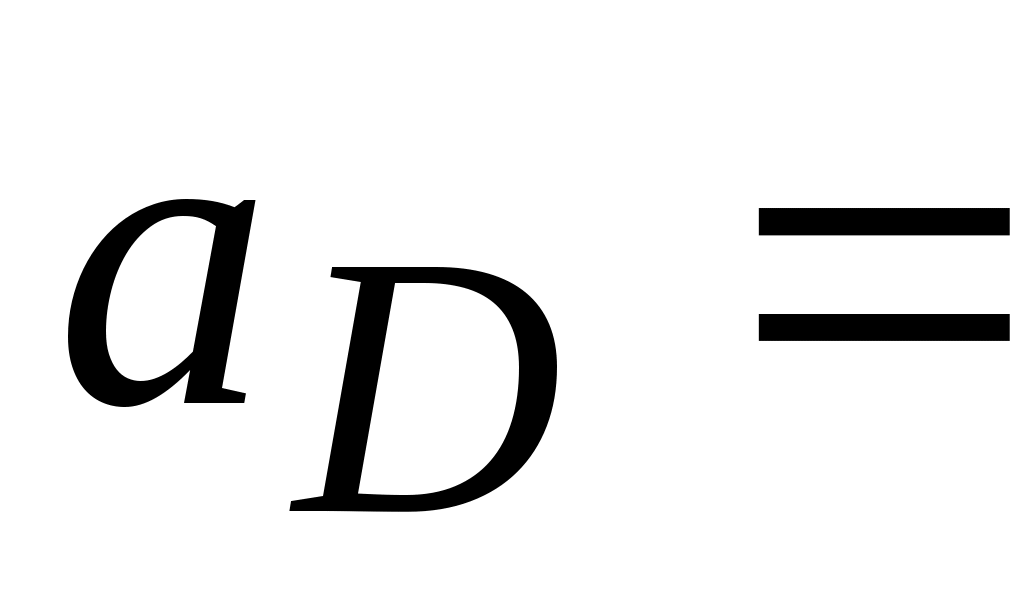
 ·
· (м/с2);
(м/с2);
ε2 =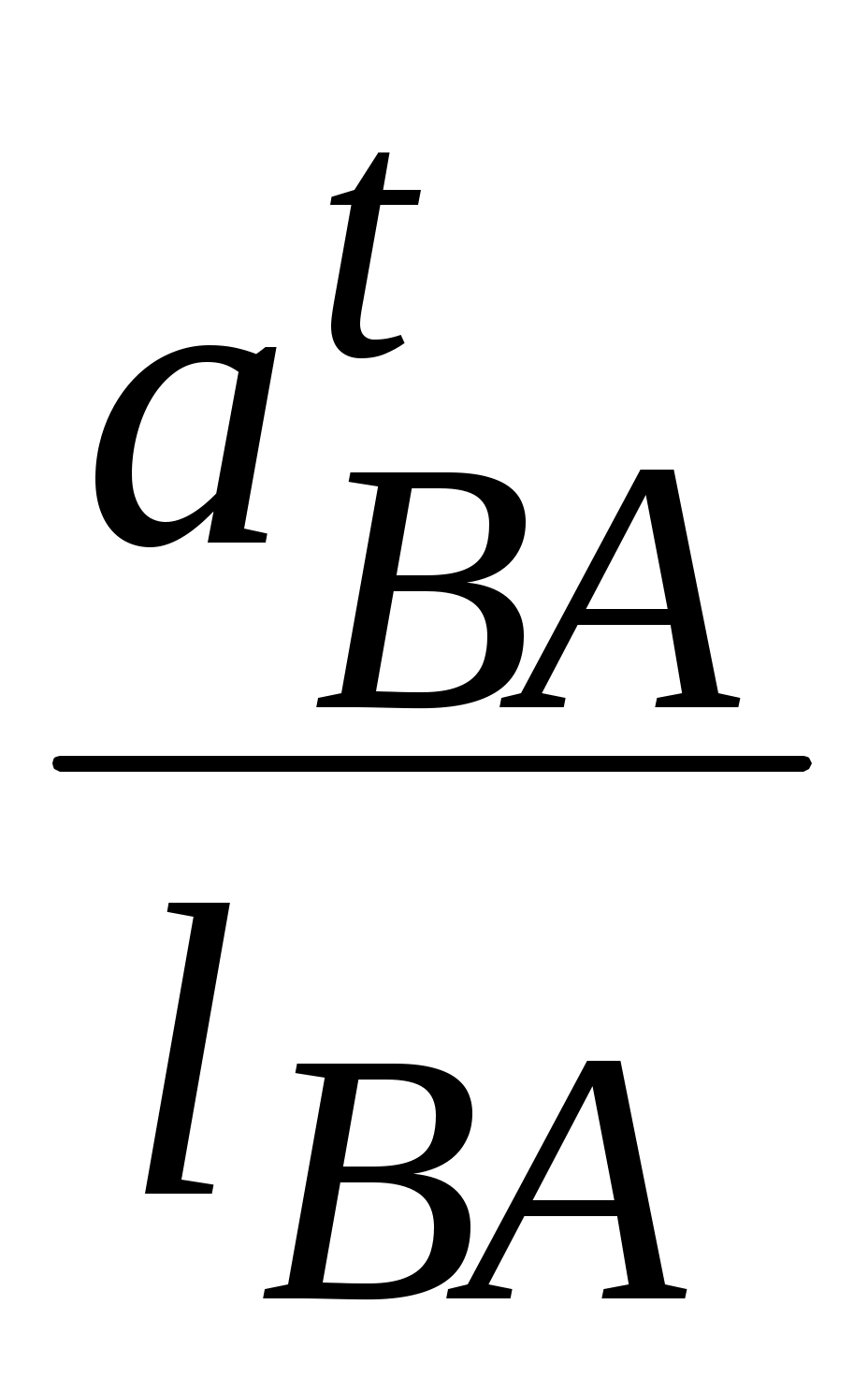 ;
;
ε3 =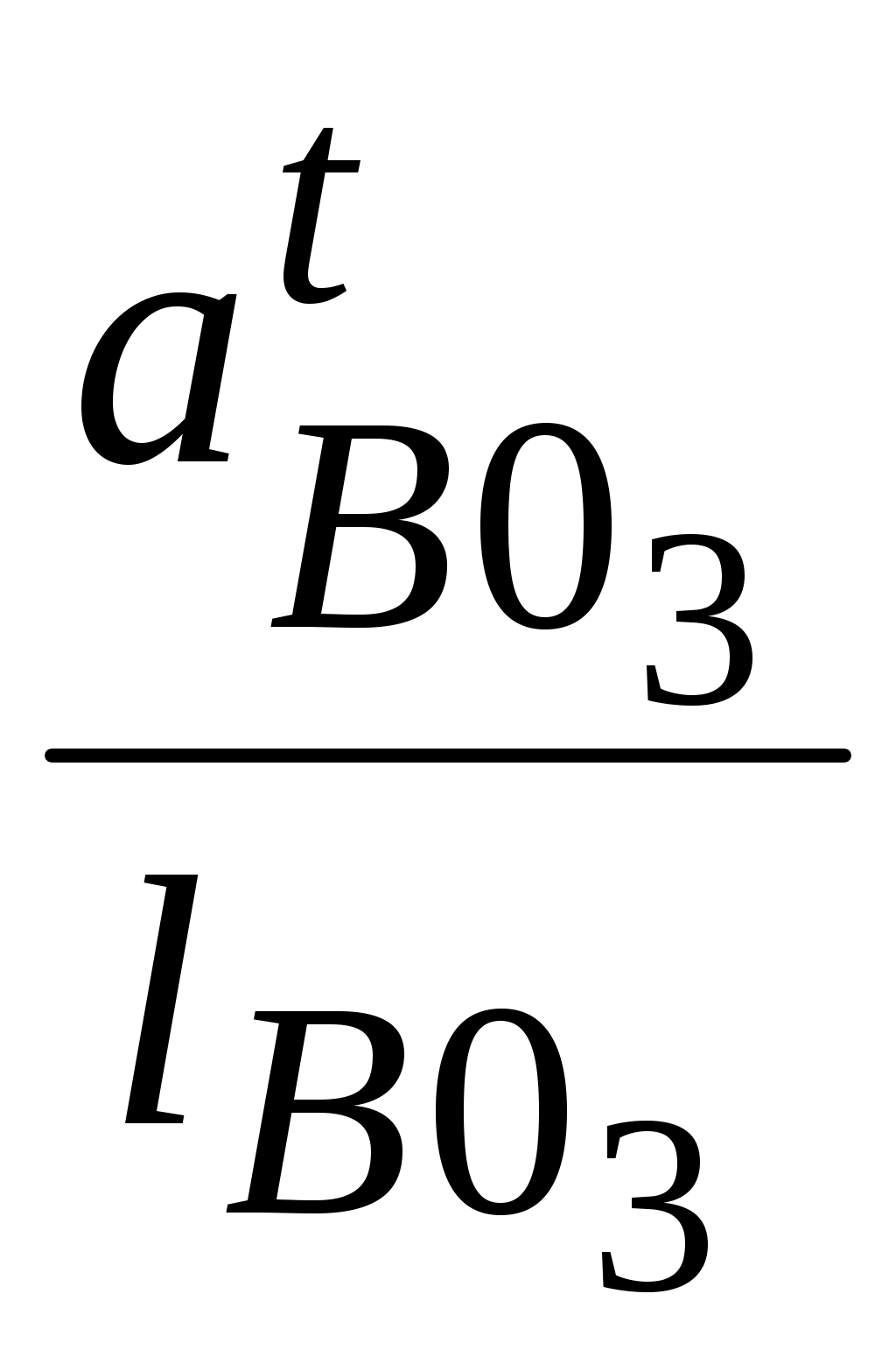 ;
;
ε4 =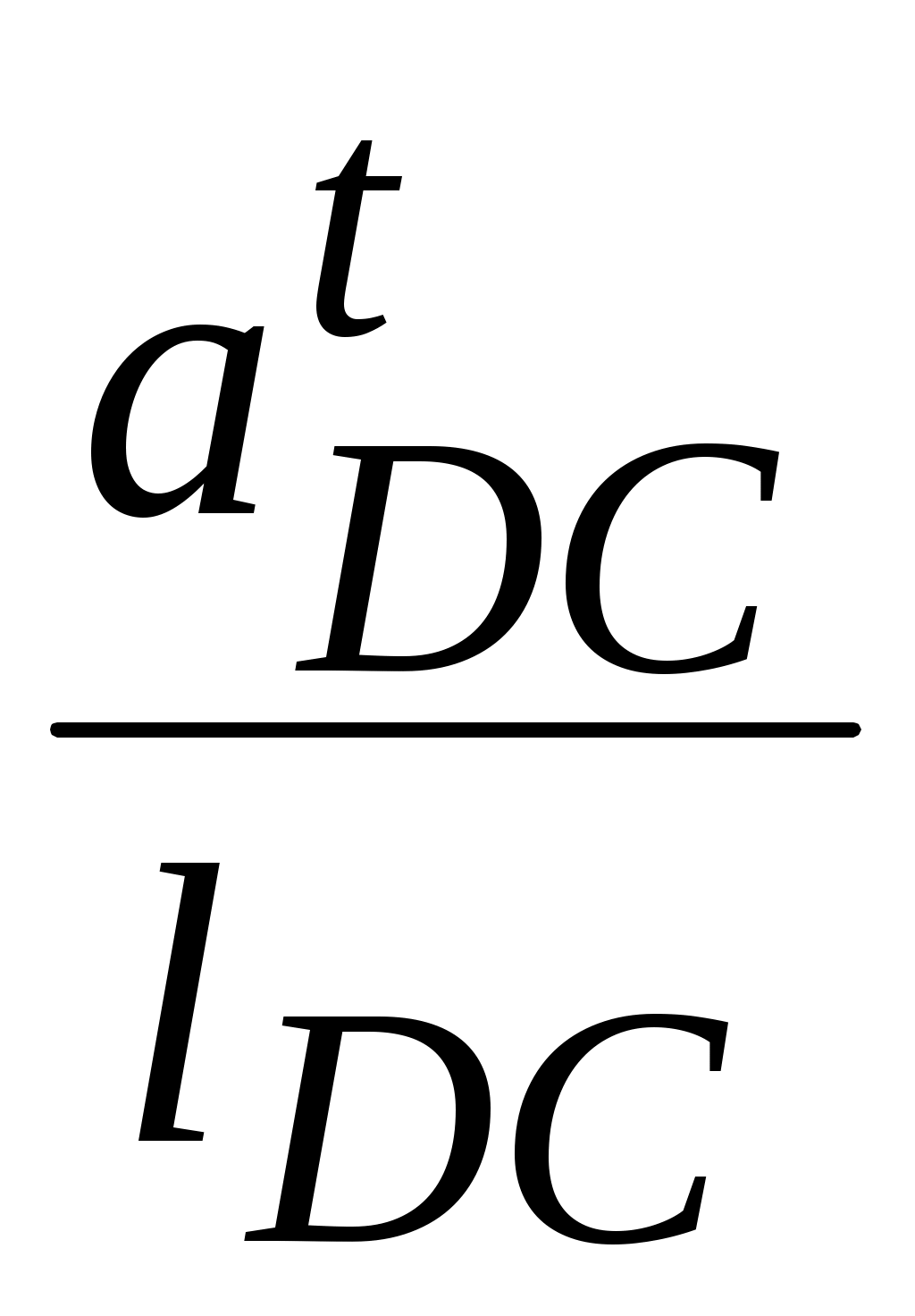 ;
;
Направление угловых ускорений определяется направлением тангенциальных ускорений. Ускорения ε2, ε3 направлены против часовой стрелки, ε4 – по часовой стрелки.
3. ПРИКЛАДНАЯ ДИНАМИКА МАШИН
3.1. Силовой расчет механизма
Основной целью прикладной динамики машин является установление взаимосвязями между силами, действующими в машине, массами движущихся её частей и кинематическими параметрами.
Все действующие нагрузки на звенья машины (рис.3.1) удобно разделить на следующие группы:
– движущая сила Fдв или момент Мдв, приложенные к ведущему звену машины со стороны двигателя. Работа этих нагрузок всегда положительна
Адв =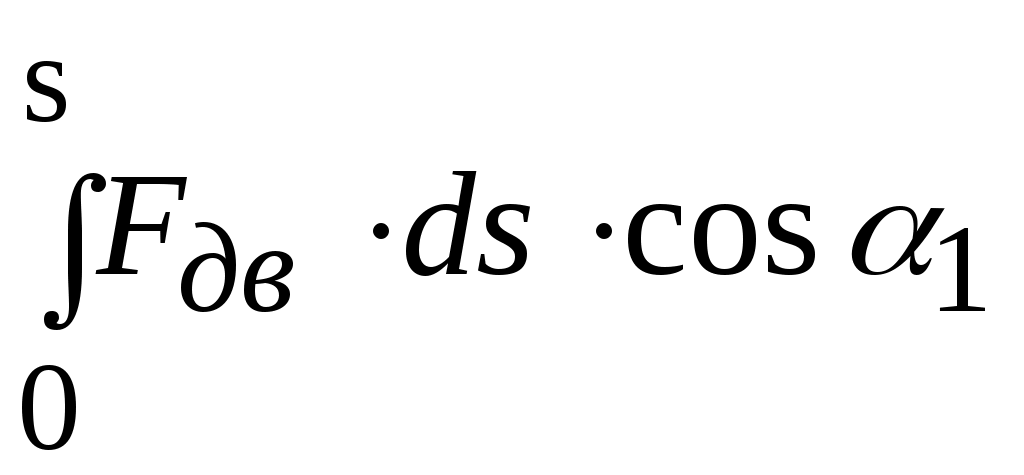 > 0;
> 0;
– сила Fс или момент М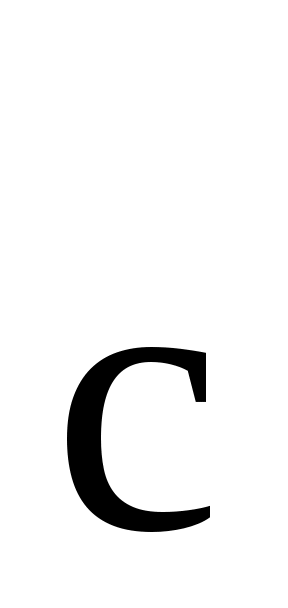 силы полезного сопротивления, приложенные к ведомому звену. Работа этой силы всегда отрицательна
силы полезного сопротивления, приложенные к ведомому звену. Работа этой силы всегда отрицательна
А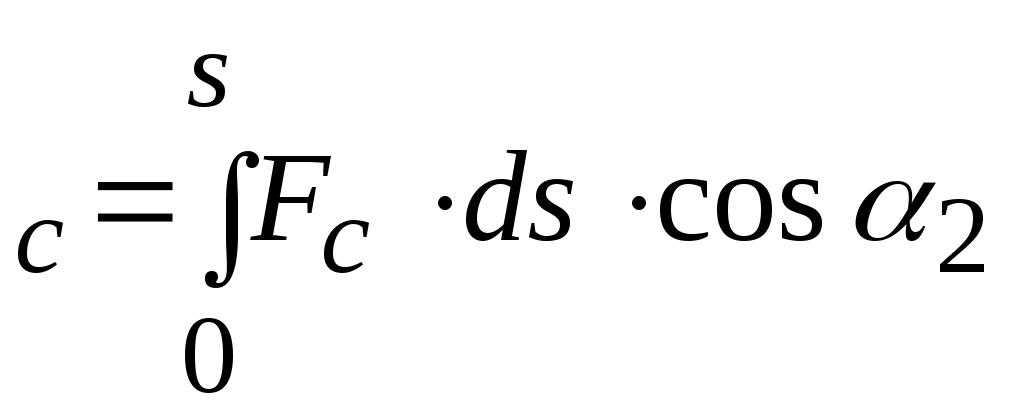 < 0;
< 0;
– силы тяжести звеньев Gί . Работа сил тяжести за один цикл движения машины равна нулю. Внутри цикла работа принимает попеременно положительное и отрицательное значение, а поэтому силы тяжести могут проявлять себя как движущие силы, так и силы сопротивления;
– силы трения Fтр и моменты сил трения Мтр в подвижных соединениях механизма. Работа сил трения всегда отрицательна. Поэтому они, главным образом, являются силами вредного сопротивления;
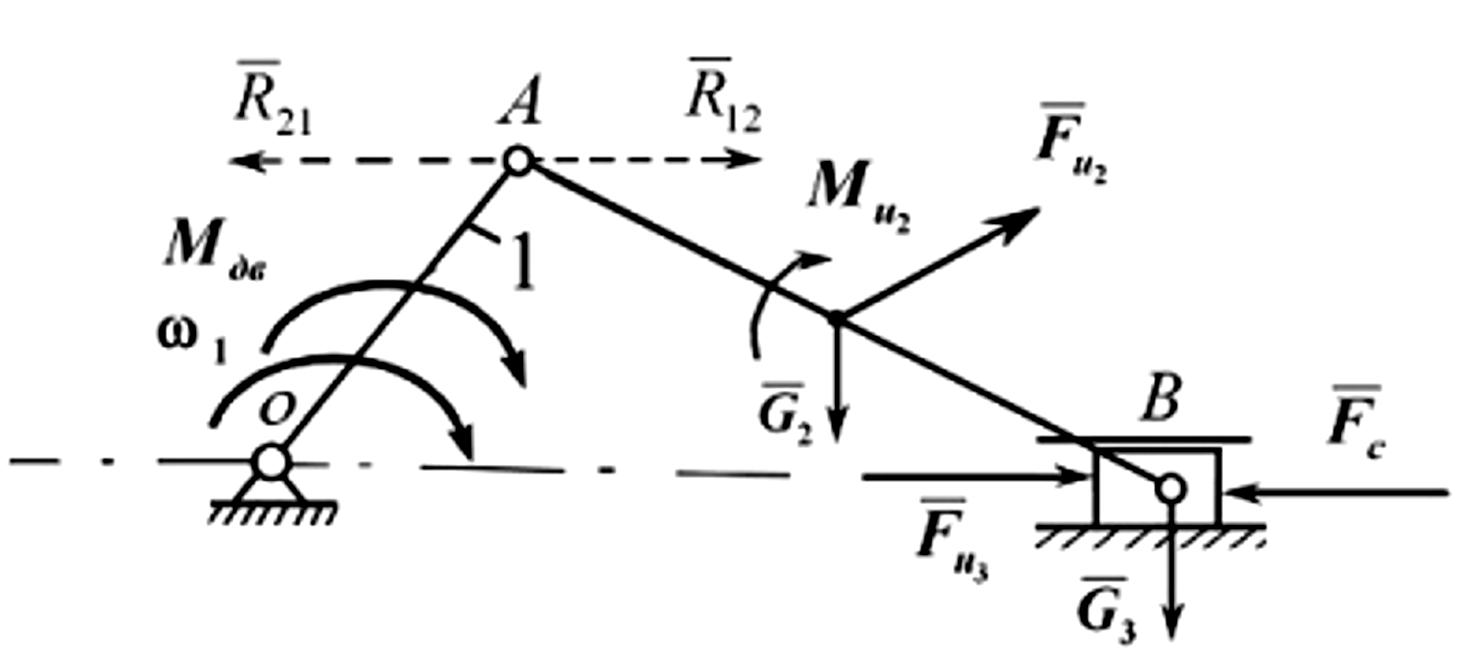
Рис.3.1. Нагрузки на звенья машины
– силы F и моменты сил инерции М
и моменты сил инерции М . Они возникают при
. Они возникают при
переменном движении звеньев;
– силы реакции Rij , с которыми звенья в подвижных соединениях воздействуют друг на друга. Эти силы действуют попарно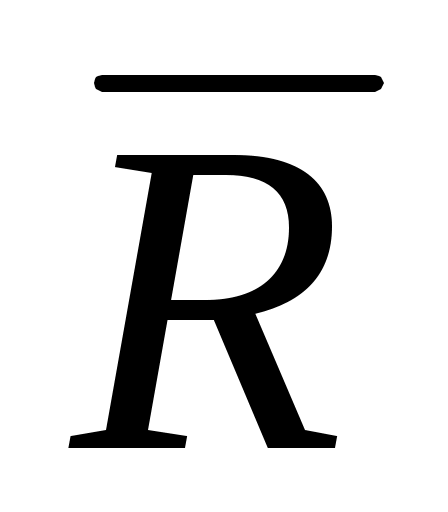 іј = –
іј = – 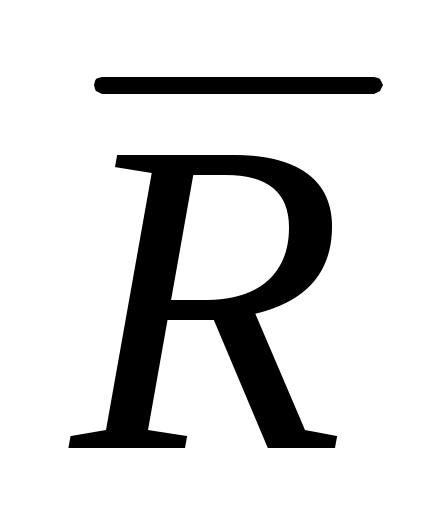 јі , суммарная их работа всегда будет равна нулю. Реакции являются быстро меняющимися силами. От их величины зависит конструкция звеньев и геометрические элементы подвижных соединений.
јі , суммарная их работа всегда будет равна нулю. Реакции являются быстро меняющимися силами. От их величины зависит конструкция звеньев и геометрические элементы подвижных соединений.
Если машина находится в состоянии покоя, то все приложенные к ней силы находятся в равновесии. При движении равновесие нарушается. Однако условие равновесия сил при движении легко формализуется, если применить метод кинетостатики. В его основе лежит принцип Даламбера – Лагранжа, который можно сформулировать следующим образом: «Если ко всем внешними силами, действующим на машину как на связанную механическую систему звеньев, добавить главные векторы и моменты сил инерции подвижных звеньев, то получим уравновешенную систему сил, позволяющую определять неизвестные реакции связей».
Из произвольно выбранной точки на чертеже (π – полюс плана) откладываем нормальную составляющую
Для определения ускорения точки В запишем векторные уравнения движения этой точки относительно 03 и относительно точки А. Имеем
Используя план скоростей (рис.2.10), вычисляем составляющие:
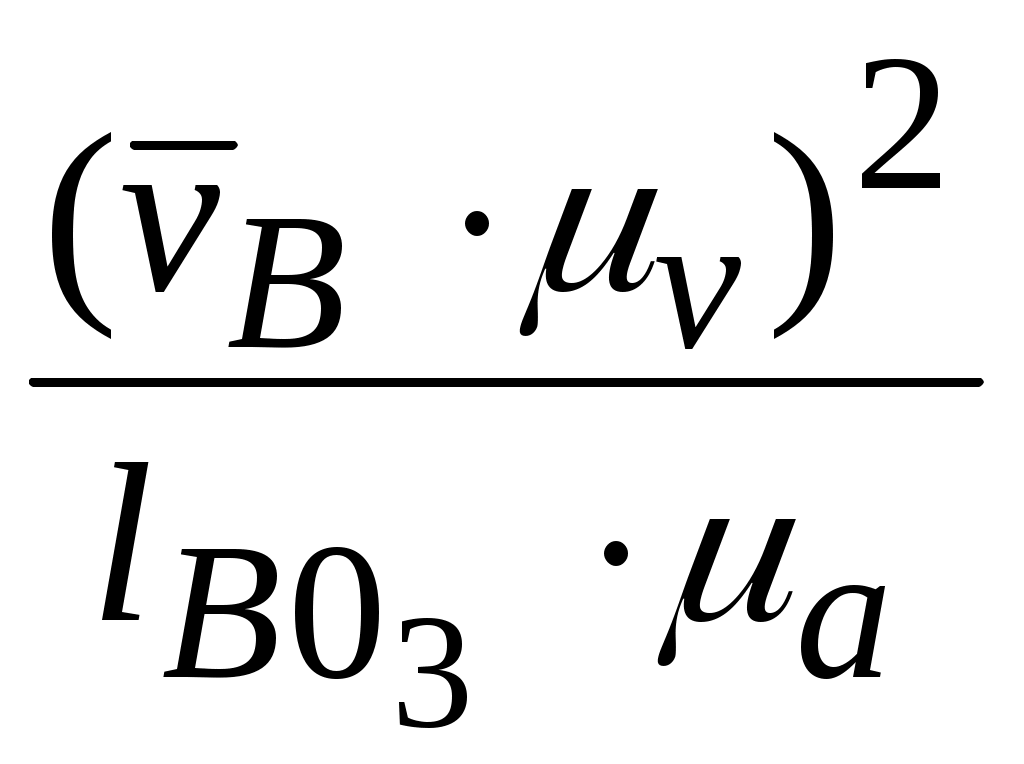 мм, или
мм, или строим вектор
Запишем векторные ускорения для определения ускорения точки D, имеем
Проводим через полюс
Определяем величины и направления линейных и угловых ускорений звеньев механизма.

Рис.2.13. План ускорений механизма компрессора
Измеряем величины векторов в мм на плане ускорений и умножаем на масштабный коэффициент плана, получаем значения в м/с2. Итак имеем
(м/с2);
ε2 =
ε3 =
ε4 =
Направление угловых ускорений определяется направлением тангенциальных ускорений. Ускорения ε2, ε3 направлены против часовой стрелки, ε4 – по часовой стрелки.
3. ПРИКЛАДНАЯ ДИНАМИКА МАШИН
3.1. Силовой расчет механизма
Основной целью прикладной динамики машин является установление взаимосвязями между силами, действующими в машине, массами движущихся её частей и кинематическими параметрами.
Все действующие нагрузки на звенья машины (рис.3.1) удобно разделить на следующие группы:
– движущая сила Fдв или момент Мдв, приложенные к ведущему звену машины со стороны двигателя. Работа этих нагрузок всегда положительна
Адв =
– сила Fс или момент М
А
– силы тяжести звеньев Gί . Работа сил тяжести за один цикл движения машины равна нулю. Внутри цикла работа принимает попеременно положительное и отрицательное значение, а поэтому силы тяжести могут проявлять себя как движущие силы, так и силы сопротивления;
– силы трения Fтр и моменты сил трения Мтр в подвижных соединениях механизма. Работа сил трения всегда отрицательна. Поэтому они, главным образом, являются силами вредного сопротивления;

Рис.3.1. Нагрузки на звенья машины
– силы F
переменном движении звеньев;
– силы реакции Rij , с которыми звенья в подвижных соединениях воздействуют друг на друга. Эти силы действуют попарно
Если машина находится в состоянии покоя, то все приложенные к ней силы находятся в равновесии. При движении равновесие нарушается. Однако условие равновесия сил при движении легко формализуется, если применить метод кинетостатики. В его основе лежит принцип Даламбера – Лагранжа, который можно сформулировать следующим образом: «Если ко всем внешними силами, действующим на машину как на связанную механическую систему звеньев, добавить главные векторы и моменты сил инерции подвижных звеньев, то получим уравновешенную систему сил, позволяющую определять неизвестные реакции связей».