Файл: Методическое пособие по дисциплине методы оптимальных решений 1 семестр Направление подготовки 080100 Экономика.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 172
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Проверяем, является ли данный опорный план оптимальным или нет. Для этого рассмотрим 4-ю строку, таблицы 8. В этой строке среди чисел
нет отрицательных. Это означает, что найденный опорный план является оптимальным и 
Следовательно, план выпуска продукции, включающий изготовление 8 изделий В и 20 изделий С, является оптимальным. При данном плане выпуска изделий полностью используется сырье I и II видов и остается неиспользованным 96 кг сырья III вида, а стоимость производимой продукции равна 400 руб.
Оптимальным планом производства продукции не предусматривается изготовление изделий А. Введение в план выпуска продукции изделий вида А привело бы к уменьшению указанной общей стоимости. Это видно из 4-й строки столбца вектора P1,где число 5 показывает, что при данном плане включение в него выпуска единицы изделия А приводит лишь к уменьшению общей величины стоимости на 5 руб.
Решение данного примера симплексным методом можно было бы проводить, используя лишь одну таблицу (таблица 9). В этой таблице последовательно записаны одна за другой все три итерации вычислительного процесса.
Таблица 9
| i | Базис | Сб | Р0 | 9 | 10 | 16 | 0 | 0 | 0 |
| | | | | P1 | P2 | P3 | p4 | p5 | Р6 |
| 1 2 3 4 1 2 3 4 1 2 3 4 | P4 р5 p6 P4 p3 p6 P2 p3 p6 | 0 0 0 0 16 0 0 16 0 | 360 192 180 0 72 24 108 384 8 20 96 400 | 18 6 5 -9 9 3/4 11/4 3 1 1/4 5/4 5 | 15 4 3 -10 9 1/2 3/2 -2 1 0 0 0 | 12 8 3 -16 0 1 0 0 0 1 0 0 | 1 0 0 0 1 0 0 0 1/9 -1/18 -1/6 2/9 | 0 1 0 0 -3/2 1/8 -3/8 2 -1/6 5/24 -1/8 5/3 | 0 0 1 0 0 0 1 0 0 0 1 0 |
1.9. Найти максимум функции
при условиях 
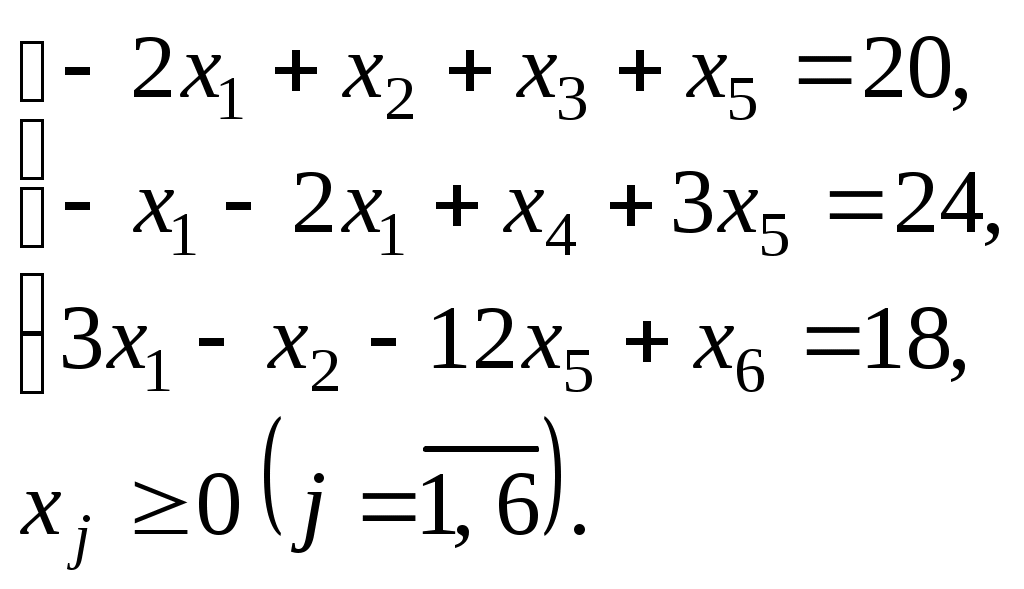
Решение. Систему уравнений задачи запишем в векторной форме:
где
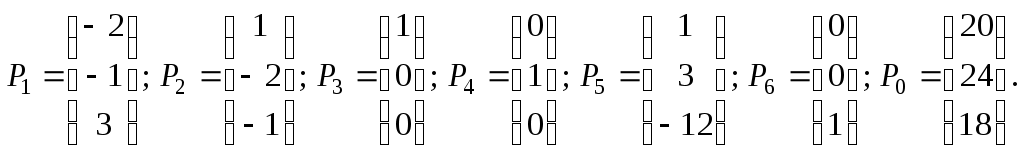
Так как среди векторов
имеется три единичных вектора, то для данной задачи можно непосредственно найти опорный план. Таковым является план Х=(0, 0, 20, 24; 0; 18). Составляем симплексную таблицу (таблица 10) и проверяем, является ли данный опорный план оптимальным.Таблица 10
i | Базис | Сб | Р0 | 2 | -6 | 0 | 0 | 5 | 0 |
| | | | | P1 | P2 | P3 | p4 | p5 | Р6 |
| 1 2 3 4 | p3 P4 p6 | 0 0 0 | 20 24 18 0 | -2 -1 3 -2 | 1 -2 -1 6 | 1 0 0 0 | 0 1 0 0 | 1 3 -12 -5 | 0 0 1 0 |
Как видно из таблицы 10, исходный опорный план не является оптимальным. Поэтому переходим к новому опорному плану. Это можно сделать, так как в столбцах векторов P1 и p5, 4-я строка которых содержит отрицательные числа, имеются положительные элементы. Для перехода к новому опорному плану введем в базис вектор p5 и исключим из базиса вектор p4. Составляем таблицу II итерации.
Таблица 11
i | Базис | Сб | Р0 | 2 | -6 | 0 | 0 | 5 | 0 |
| | | | | P1 | P2 | P3 | p4 | p5 | Р6 |
| 1 2 3 | p3 P5 p6 | 0 5 0 | 12 8 114 40 | -5/3 -1/3 -1 -11/3 | 5/3 -2/3 -9 8/3 | 1 0 0 0 | -1/3 1/3 4 5/3 | 0 1 0 0 | 0 0 1 0 |
Как видно из таблицы 11, новый опорный план задачи не является оптимальным, так как в 4-й строке столбца вектора P1стоит отрицательное число -11/3. Поскольку в столбце этого вектора нет положительных элементов, данная задача не имеет оптимального плана.
1.6. Прямая и двойственная задача линейного программирования. Геометрическая интерпретация двойственной задачи.
Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной или прямой. Дадим определение двойственной задачи по отношению к общей задаче линейного программирования, состоящей в нахождении максимального значения функции
(32)при условиях
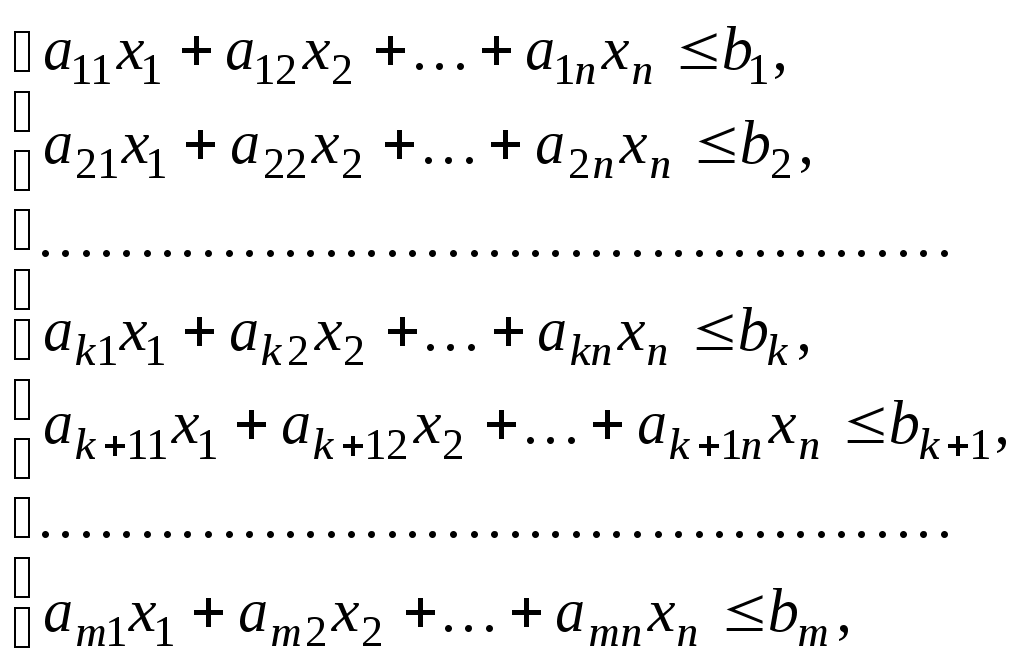(33)
(34)Определение 1.12. Задача, состоящая в нахождении минимального значения функции
(35)при условиях
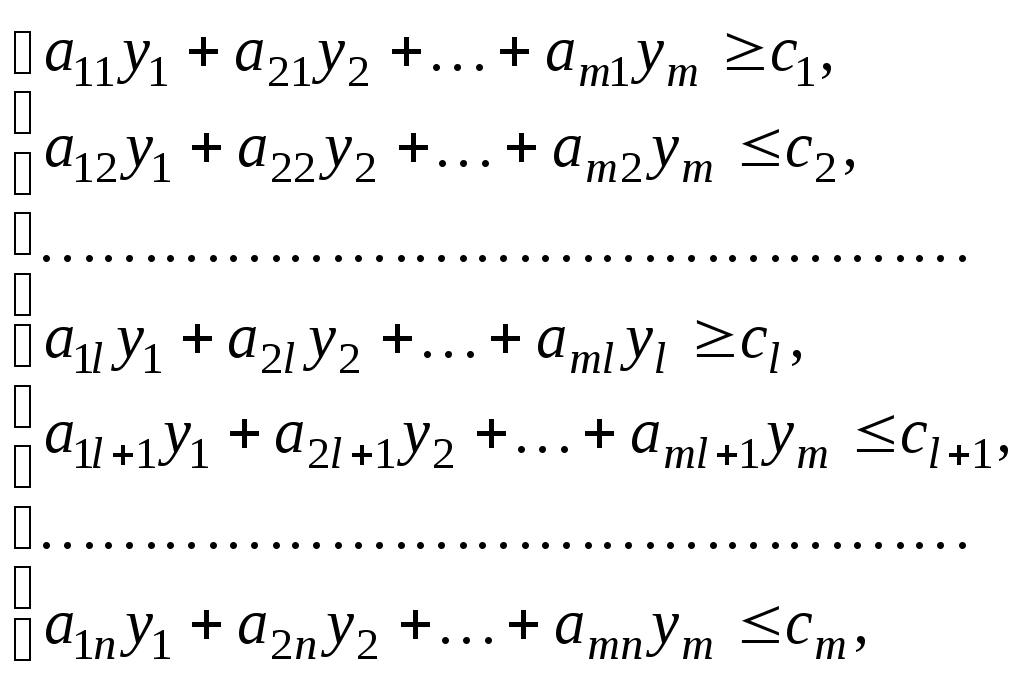(36)
(37)называется двойственной по отношению к задаче (32) - (34). Задачи (32) - (34) и (35) - (37) образуют пару задач, называемую в линейном программировании двойственной парой. Сравнивая две сформулированные задачи, видим, что двойственная задача по отношению к исходной составляется согласно следующим правилам:
1. Целевая функция исходной задачи (32) - (34) задается на максимум, а целевая функция двойственной (35) - (37) — на минимум.
2. Матрица
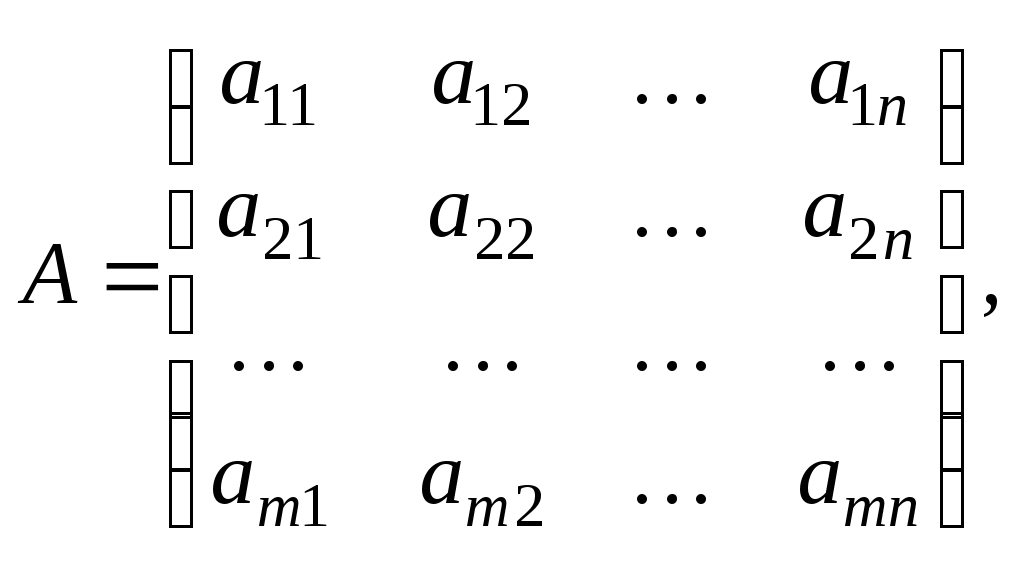(38)составленная из коэффициентов при неизвестных в системе ограничений (33) исходной задачи (32) - (34), и аналогичная матрица
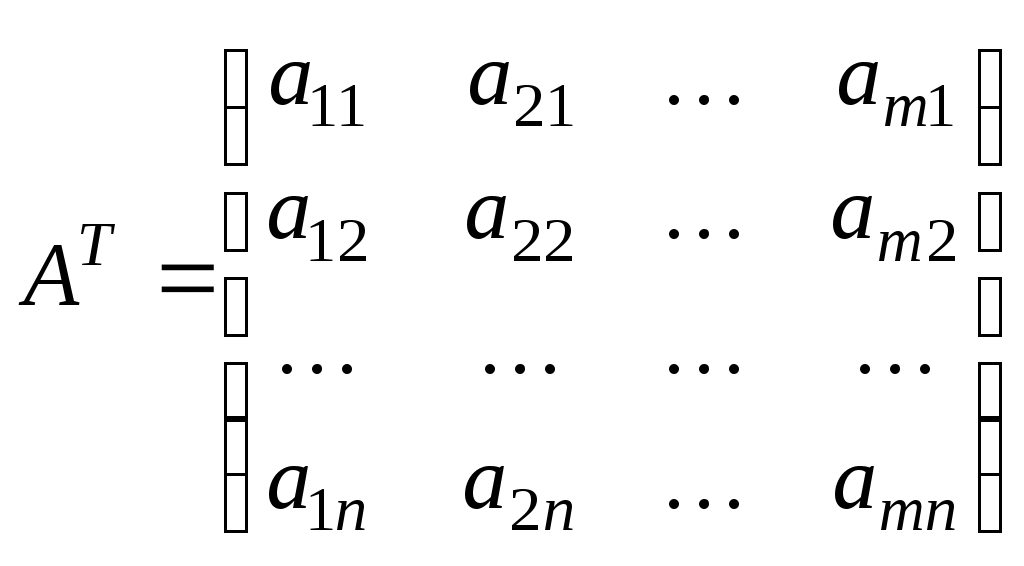(39)в двойственной задаче (35) - (37) получаются друг из друга транспонированием (т. е. заменой строк столбцами, а столбцов — строками).
3. Число переменных в двойственной задаче (35) - (37) равно числу соотношений в системе (33) исходной задачи (32) - (34), а число ограничений в системе (36) двойственной задачи — числу переменных в исходной задаче.
4. Коэффициентами при неизвестных в целевой функции (35) двойственной задачи (35) - (37) являются свободные члены в системе (33) исходной задачи (32) - (34), а правыми частями в соотношениях системы (36) двойственной задачи — коэффициенты при неизвестных в целевой функции (32) исходной задачи.
5. Если переменная xj исходной задачи (32) - (34) может принимать только лишь положительные значения, то j-е условие в системе (36) двойственной задачи (35) - (37) является неравенством вида «». Если же переменная xj может принимать как положительные, так и отрицательные значения, то 1-е соотношение в системе (54) представляет собой уравнение. Аналогичные связи имеют место между ограничениями (33) исходной задачи (32) - (34) и переменными двойственной задачи (35) - (37). Если i-е соотношение в системе (33) исходной задачи является неравенством, то i-я переменная двойственной задачи
. В противном случае переменная уj может принимать как положительные, так и отрицательные значения.Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения (33) прямой задачи и соотношения (36) двойственной задачи являются неравенствами вида «». Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.
1.10. Составить двойственную задачу по отношению к задаче, состоящей в максимизации функции
(40)при условиях
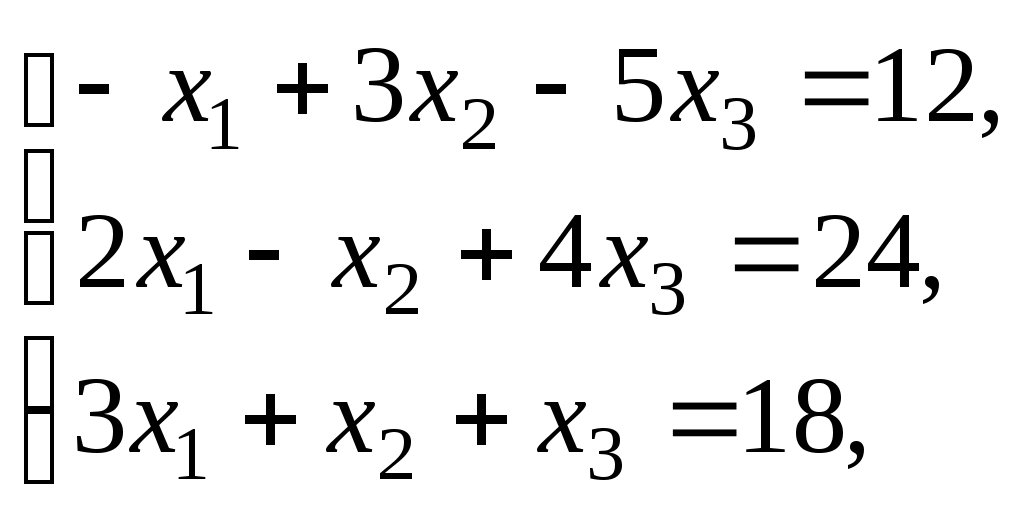(41)
(42)Решение. Для данной задач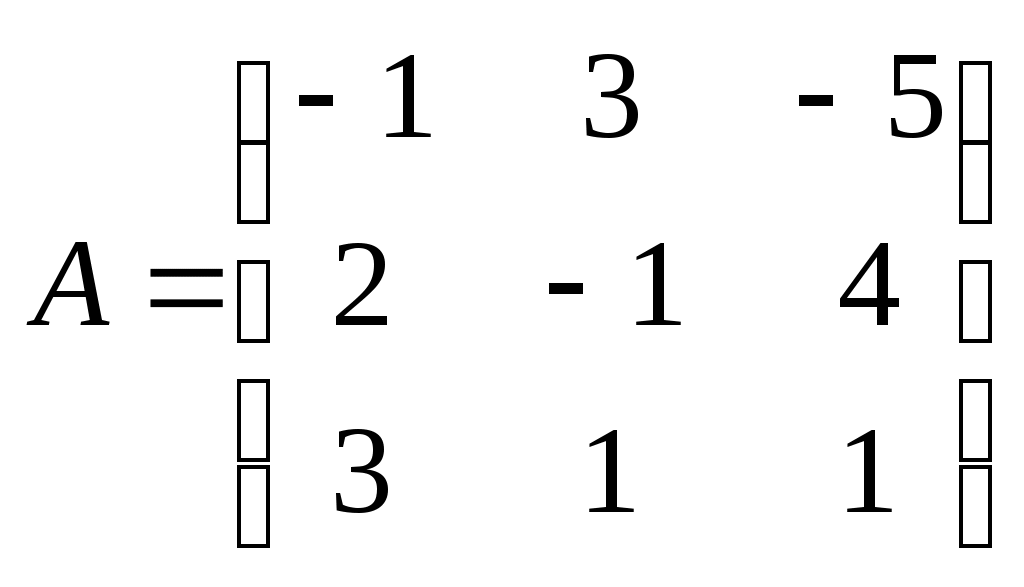и
и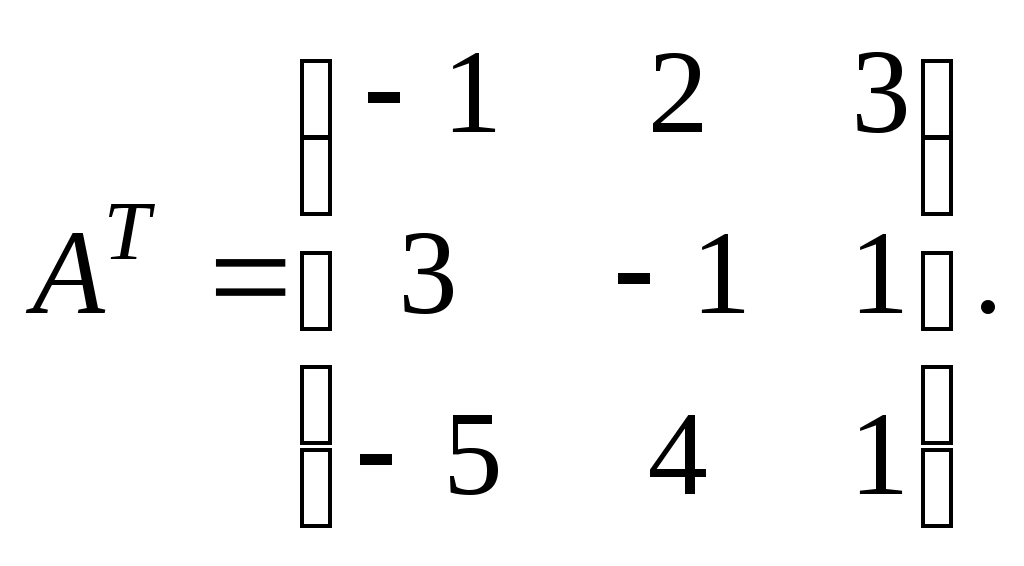 
Число переменных в двойственной задаче равно числу уравнений в системе (41), т. е. равно трем. Коэффициентами в целевой функции двойственной задачи являются свободные члены системы уравнений (41), т.е. числа 12, 24, 18.
Целевая функция исходной задачи (40) - (42) исследуется на максимум, а система условий (41) содержит только уравнения. Поэтому в двойственной задаче целевая функция исследуется на минимум, а ее переменные могут принимать любые значения (в том числе и отрицательные). Так как все три переменные исходной задачи (40) - (42) принимают только лишь неотрицательные значения, то в системе условий двойственной задачи должны быть три неравенства вида «». Следовательно, для задачи (40) - (42) двойственная задача такова: найти минимум функции