Файл: Методическое пособие по дисциплине методы оптимальных решений 1 семестр Направление подготовки 080100 Экономика.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 168
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
О(0; 0). Координаты этой точки удовлетворяют неравенству 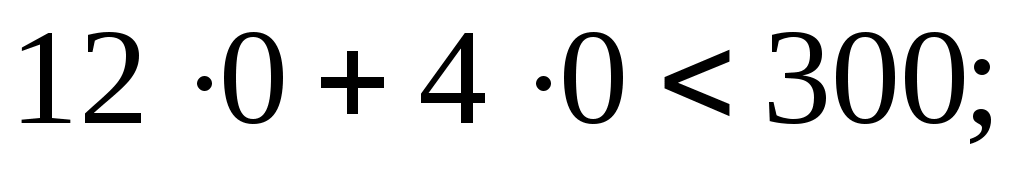 значит, полуплоскость, которой принадлежит точка О(0; 0), определяется неравенством
значит, полуплоскость, которой принадлежит точка О(0; 0), определяется неравенством 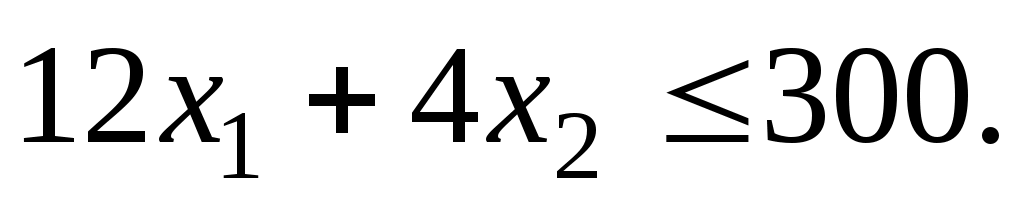 Это и показано стрелками на рис. 5.
Это и показано стрелками на рис. 5.
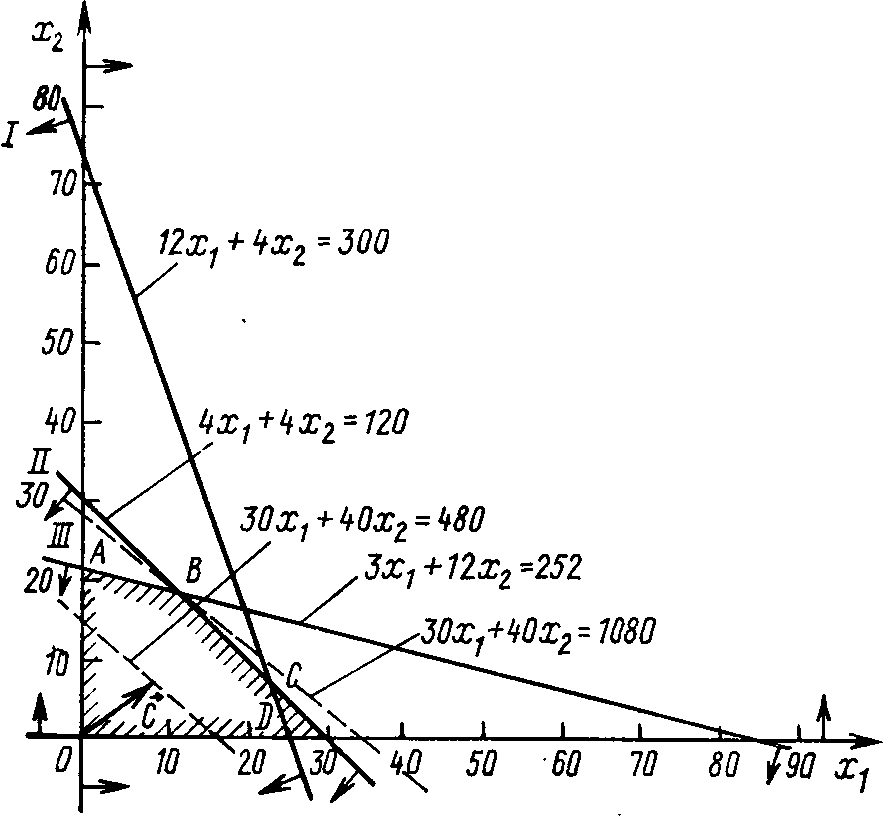
Рис. 5
Пересечение полученных полуплоскостей и определяет многоугольник решений данной задачи.
Как видно из рис. 5, многоугольником решений является пятиугольник OABCD. Координаты любой точки, принадлежащей этому пятиугольнику, удовлетворяют данной системе неравенств и условию неотрицательности переменных. Поэтому сформулированная задача будет решена, если мы сможем найти точку, принадлежащую пятиугольнику OABCD, в которой функция Fпринимает максимальное значение. Чтобы найти указанную точку, построим вектор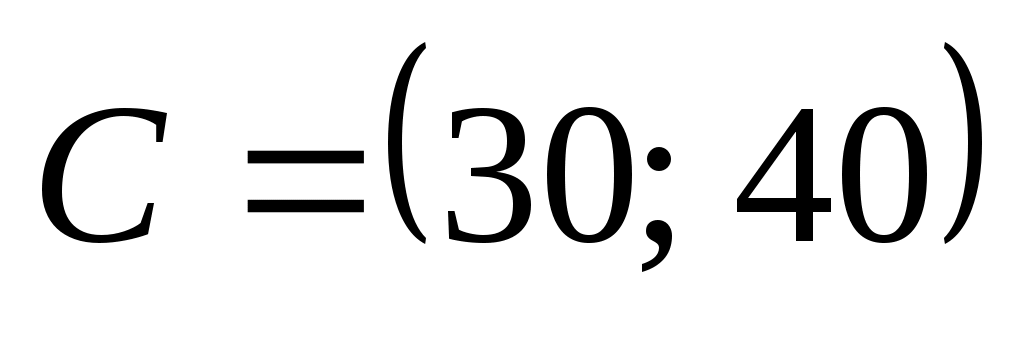 и прямую
и прямую 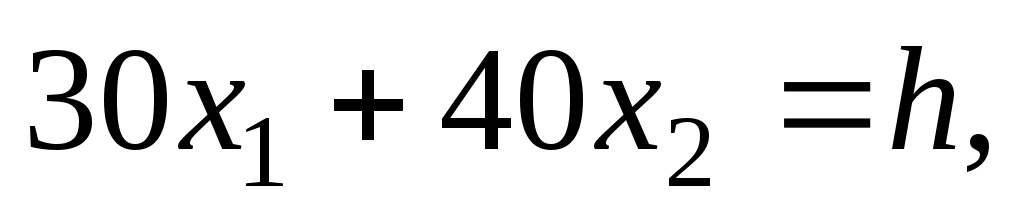 где h — некоторая постоянная такая, что прямая
где h — некоторая постоянная такая, что прямая 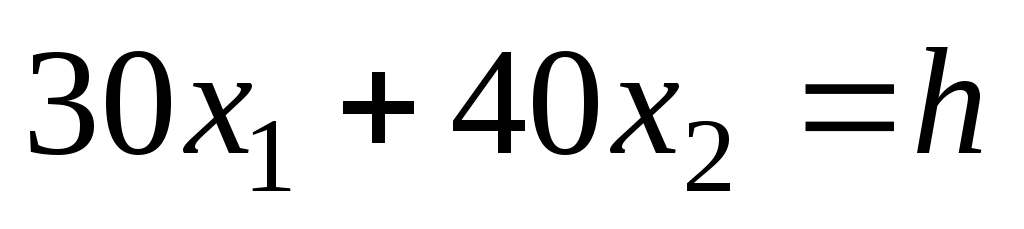 имеет общие точки с многоугольником решений. Положим, например, h = 480 и построим прямую
имеет общие точки с многоугольником решений. Положим, например, h = 480 и построим прямую 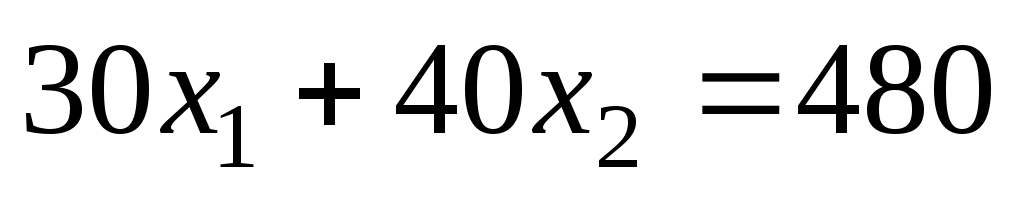 (рис. 5).
(рис. 5).
Если теперь взять какую-нибудь точку, принадлежащую построенной прямой и многоугольнику решений, то ее координаты определяют такой план производства изделий А и В, при котором прибыль от их реализации равна 480 руб. Далее, полагая h равным некоторому числу, большему чем 480, мы будем получать различные параллельные прямые. Если они имеют общие точки с многоугольником решений, то эти точки определяют планы производства изделий А и В, при которых прибыль от их реализации превзойдет 480 руб.
Перемещая построенную прямую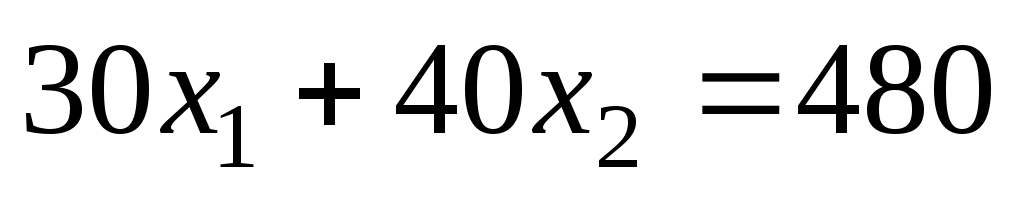 в направлении вектора
в направлении вектора 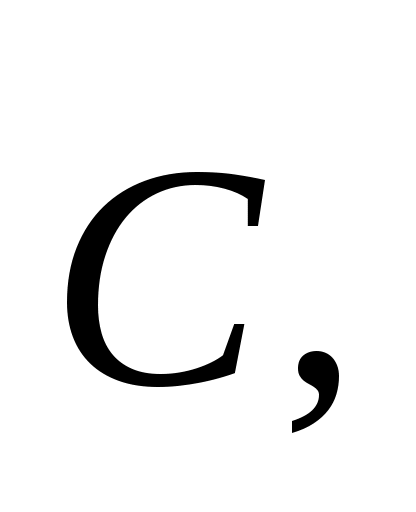 видим, что последней общей точкой ее с многоугольником решений задачи служит точка
видим, что последней общей точкой ее с многоугольником решений задачи служит точка
В. Координаты этой точки и определяют план выпуска изделий А и В, при котором прибыль от их реализации является максимальной.
Найдем координаты точки В как точки пересечения прямых II и III. Следовательно, ее координаты удовлетворяют уравнениям этих прямых
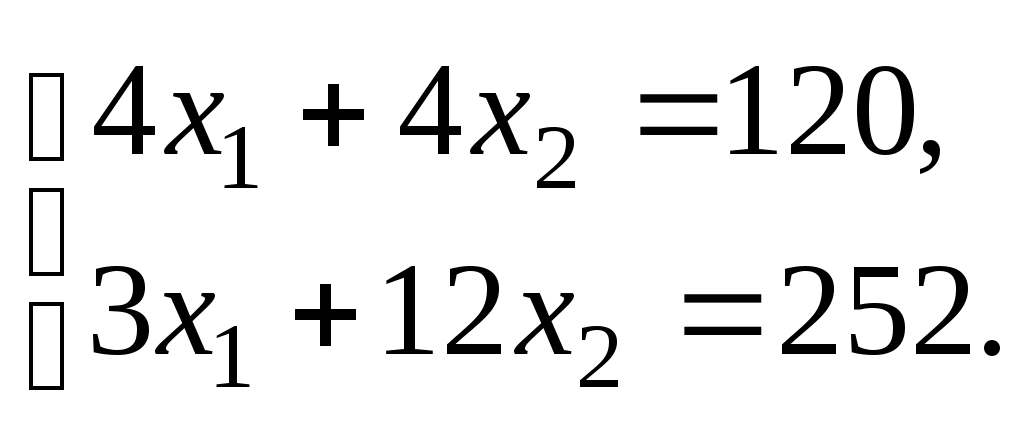
Решив эту систему уравнений, получим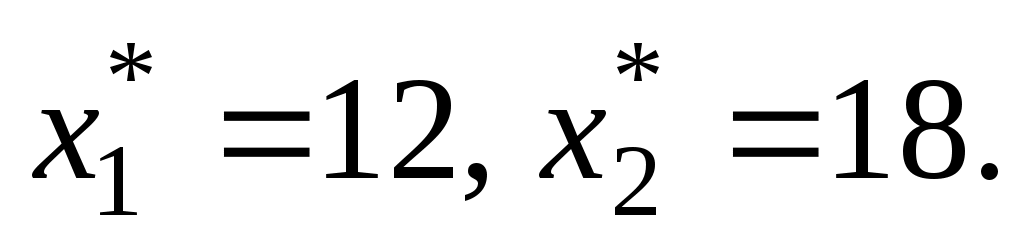 Следовательно, если предприятие изготовит 12 изделий вида А и 18 изделий вида В, то оно получит максимальную прибыль, равную
Следовательно, если предприятие изготовит 12 изделий вида А и 18 изделий вида В, то оно получит максимальную прибыль, равную 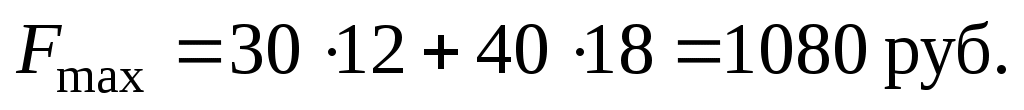
1.7. Найти максимум и минимум функции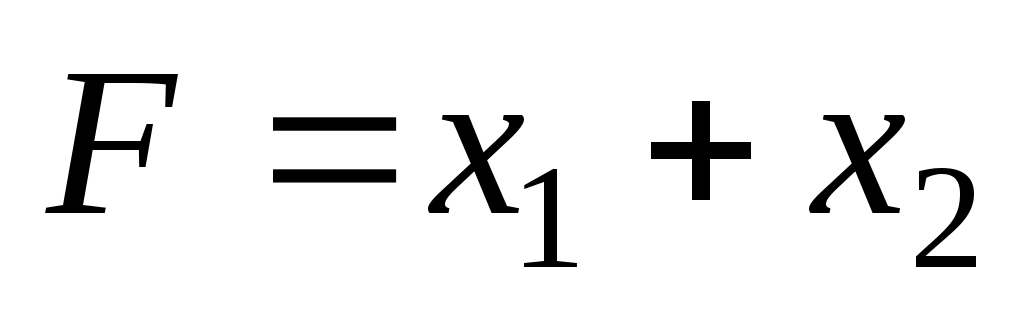 при условиях
при условиях
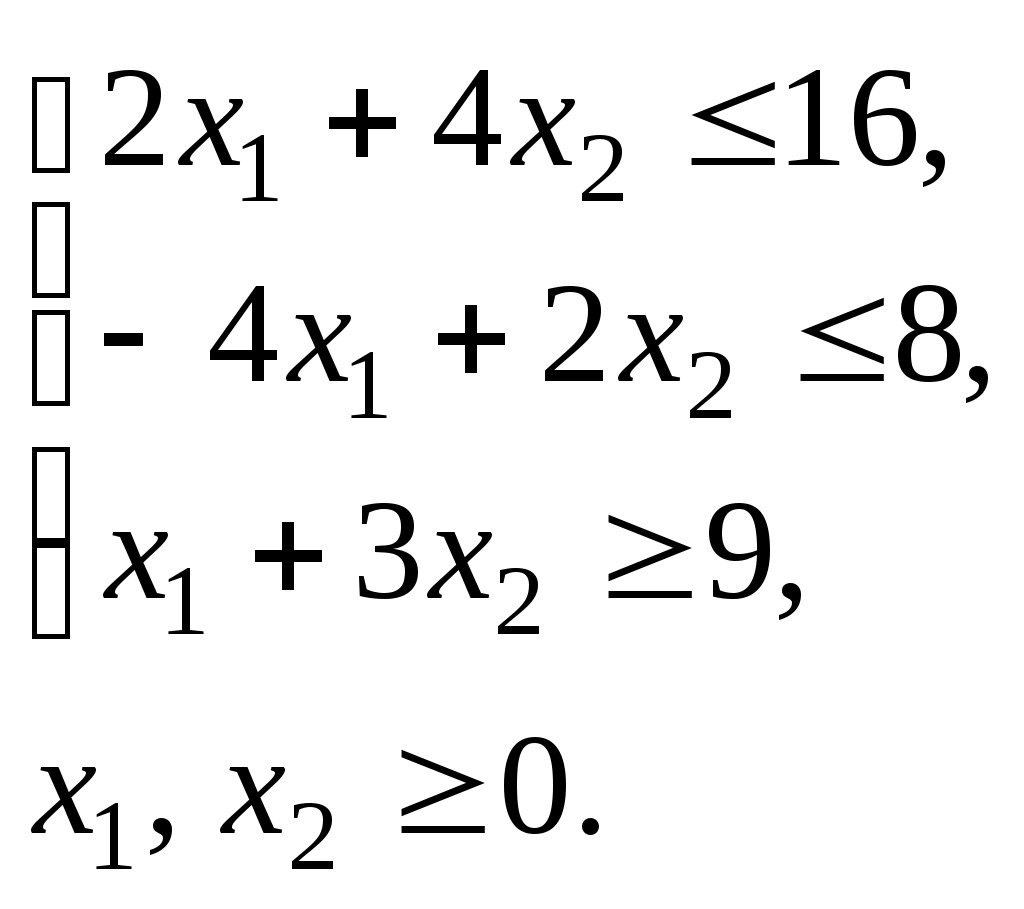
Решение. Построим многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств:

Построив полученные прямые, найдем соответствующие полуплоскости и их пересечение (рис. 6).
Как видно из рис. 6, многоугольником решений задачи является треугольник АВС. Координаты точек этого треугольника удовлетворяют условию неотрицательности и неравенствам системы ограничений задачи. Следовательно, задача будет решена, если среди точек треугольника АВС найти такие, в которых функция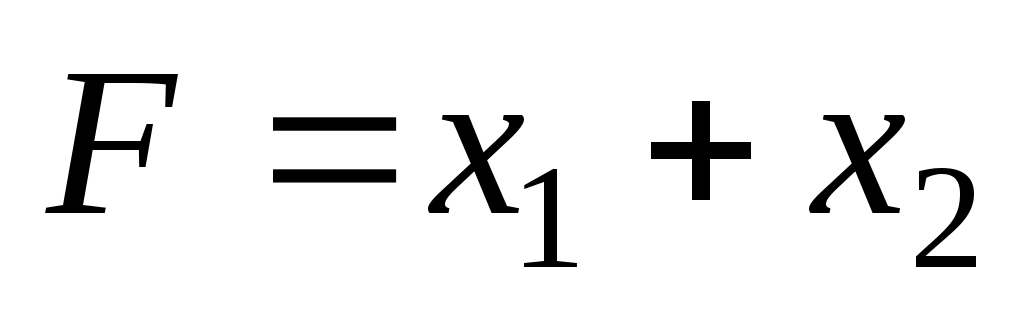 принимает максимальное и минимальное значения. Для нахождения этих точек построим прямую
принимает максимальное и минимальное значения. Для нахождения этих точек построим прямую 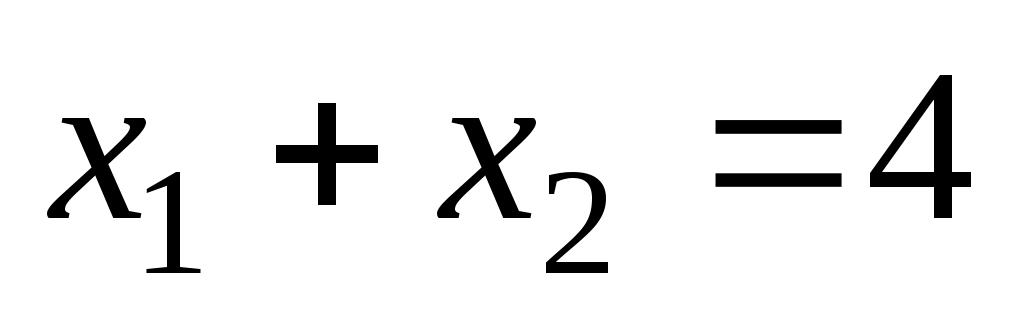 (число 4 взято произвольно) и вектор
(число 4 взято произвольно) и вектор 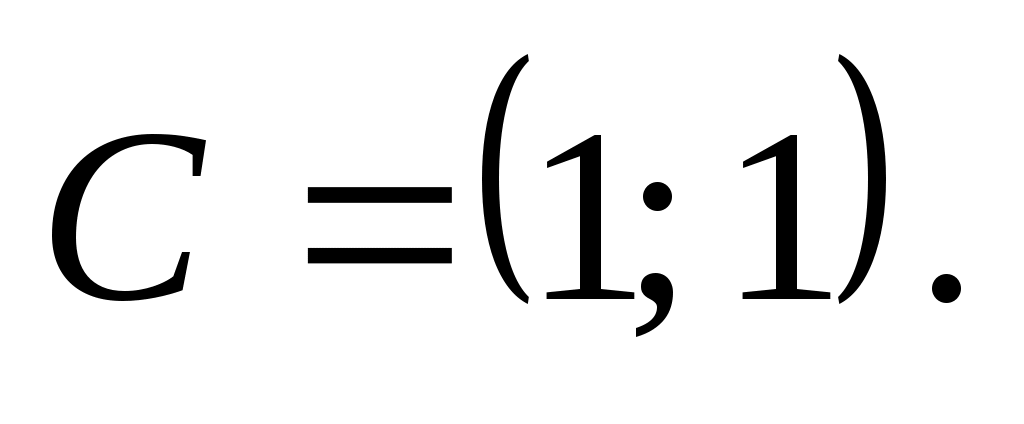
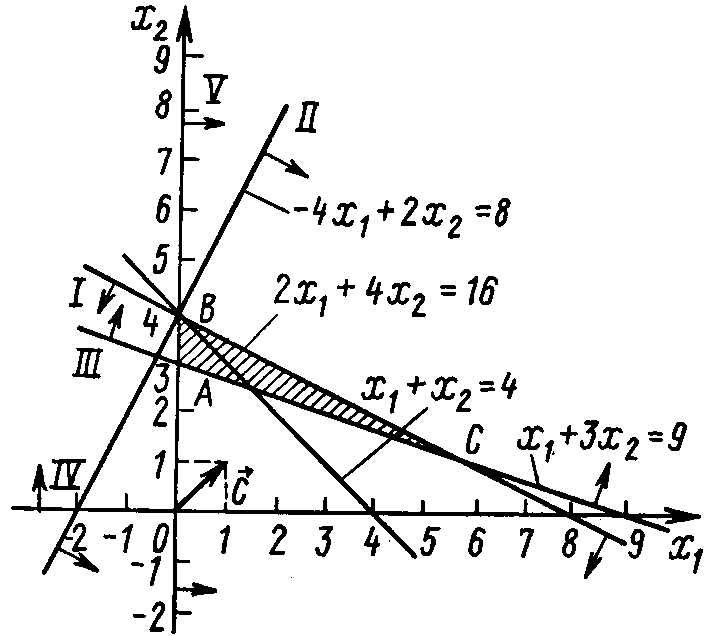
Рис. 6
Передвигая данную прямую параллельно самой себе в направлении вектора видим, что ее последней общей точкой с многоугольником решений задачи является точка С.
видим, что ее последней общей точкой с многоугольником решений задачи является точка С.
Следовательно, в этой точке функция F принимает максимальное значение. Так как С — точка пересечения прямых I и II, то ее координаты удовлетворяют уравнениям этих прямых:
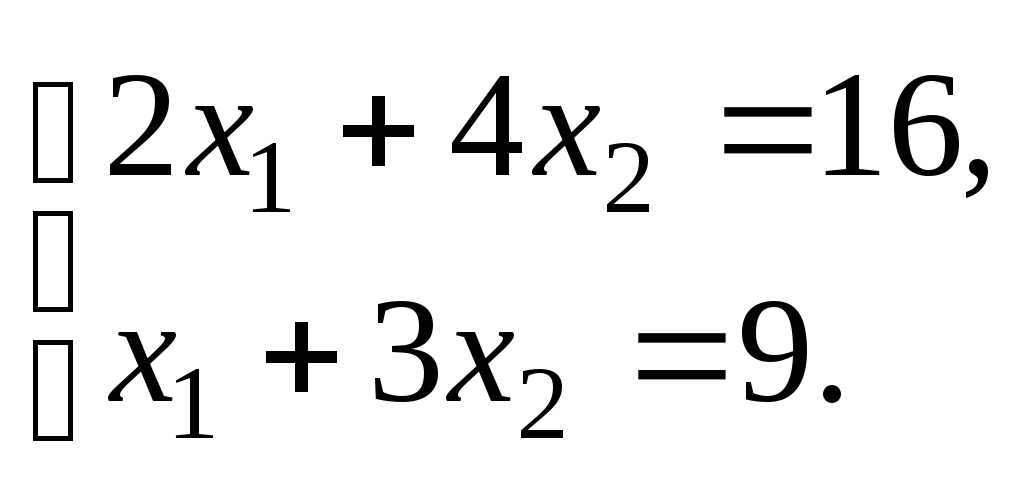
Решив эту систему уравнений, получим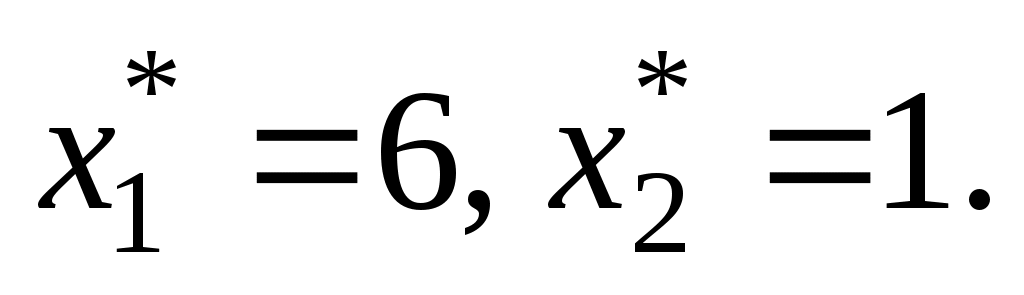 Таким образом, максимальное значение функции
Таким образом, максимальное значение функции 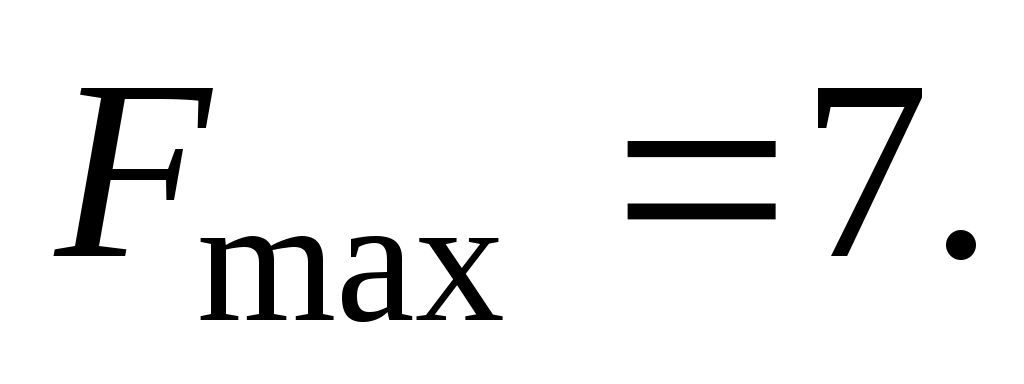
Для нахождения минимального значения целевой функции задачи передвигаем прямую в направлении, противоположном направлению вектора
в направлении, противоположном направлению вектора  В этом случае, как видно из рис. 6, последней общей точкой прямой с многоугольником решений задачи является точка А. Следовательно, в этой точке функция F принимает минимальное значение. Для определения координат точки А решаем систему уравнений
В этом случае, как видно из рис. 6, последней общей точкой прямой с многоугольником решений задачи является точка А. Следовательно, в этой точке функция F принимает минимальное значение. Для определения координат точки А решаем систему уравнений

откуда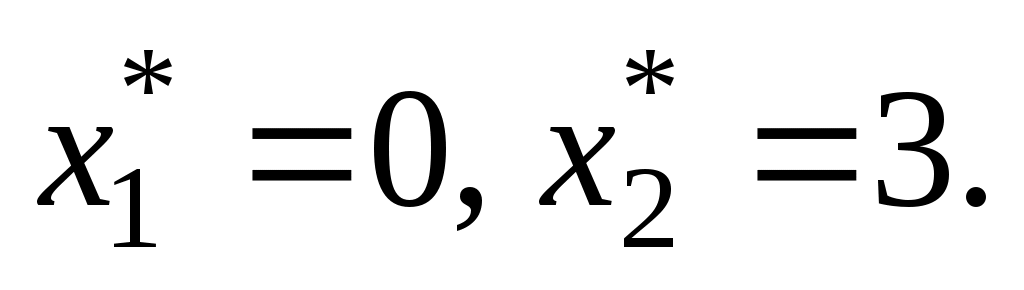 Подставляя найденные значения переменных в целевую функцию, получим
Подставляя найденные значения переменных в целевую функцию, получим 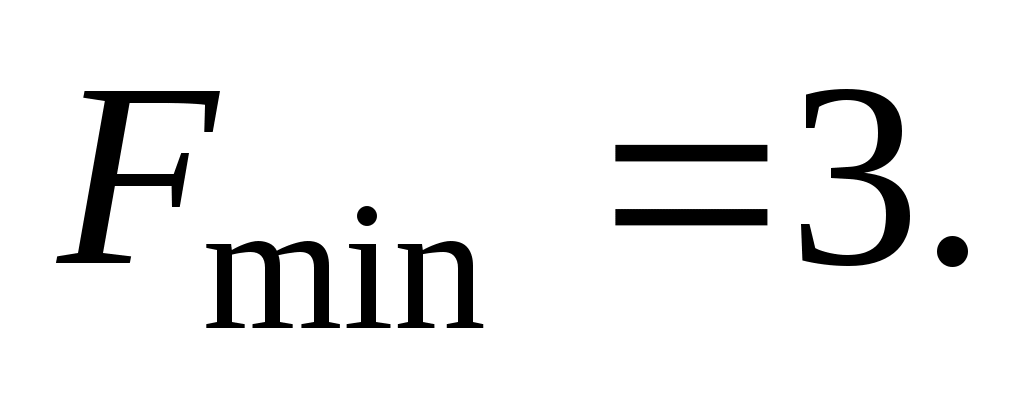
Решение любой задачи линейного программирования можно найти симплексным методом. Прежде чем применять указанный метод, следует записать исходную задачу в форме основной задачи линейного программирования, если она не имеет такой формы записи.
Симплексный метод решения задачи линейного программирования основан на пеереходе от одного опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план и каждый ее опорный план является невырожденным). Указанный переход возможен, если известен какой-нибудь исходный опорный план. Рассмотрим задачу, для которой этот план можно непосредственно записать.
Пусть требуется найти максимальное значение функции

при условиях
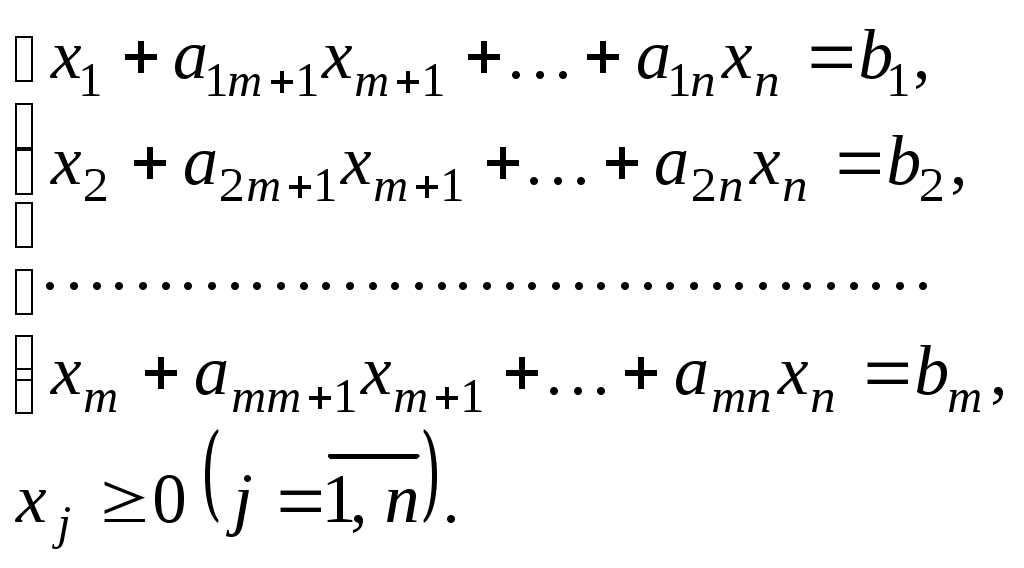
Здесь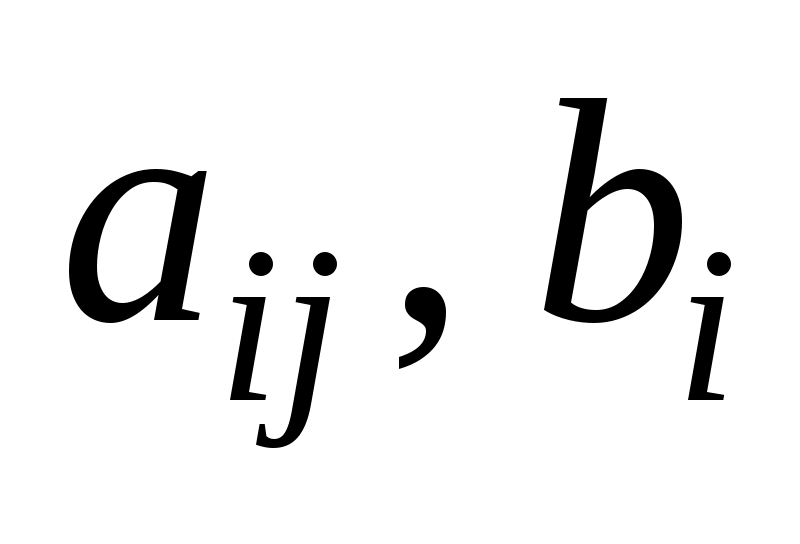 и
и 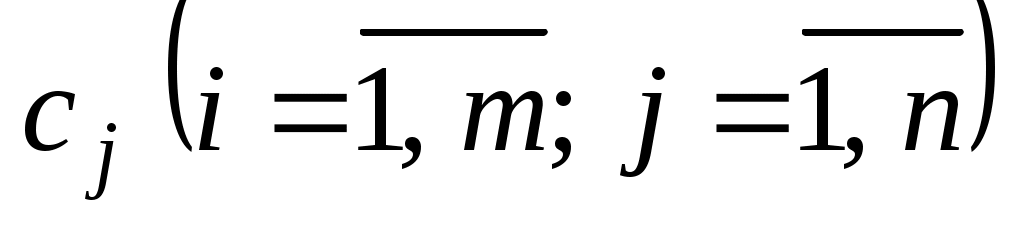 — заданные постоянные числа
— заданные постоянные числа 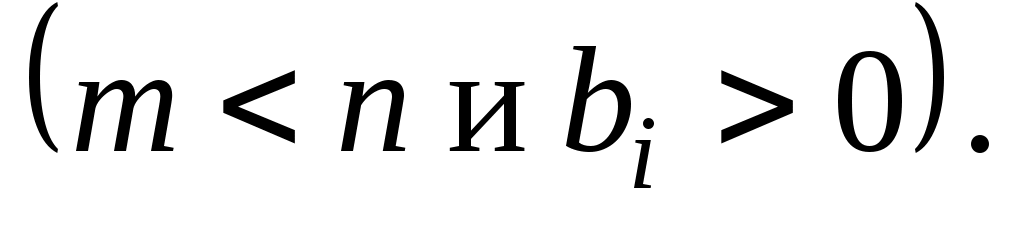
Векторная форма данной задачи имеет следующий вид: найти максимум функции
 (22)
(22)
при условиях
 (23)
(23)
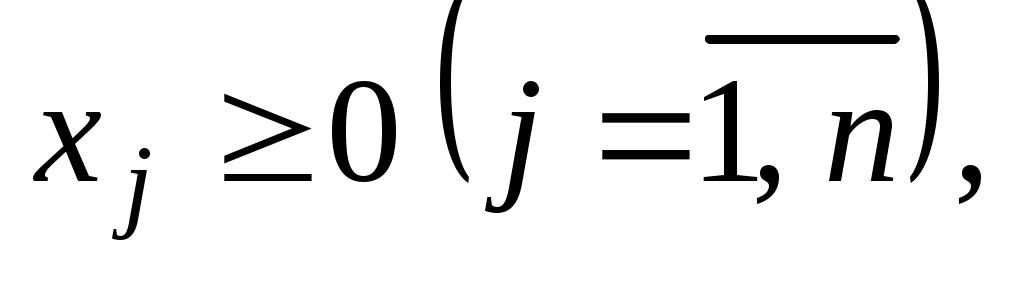 (24)
(24)
где
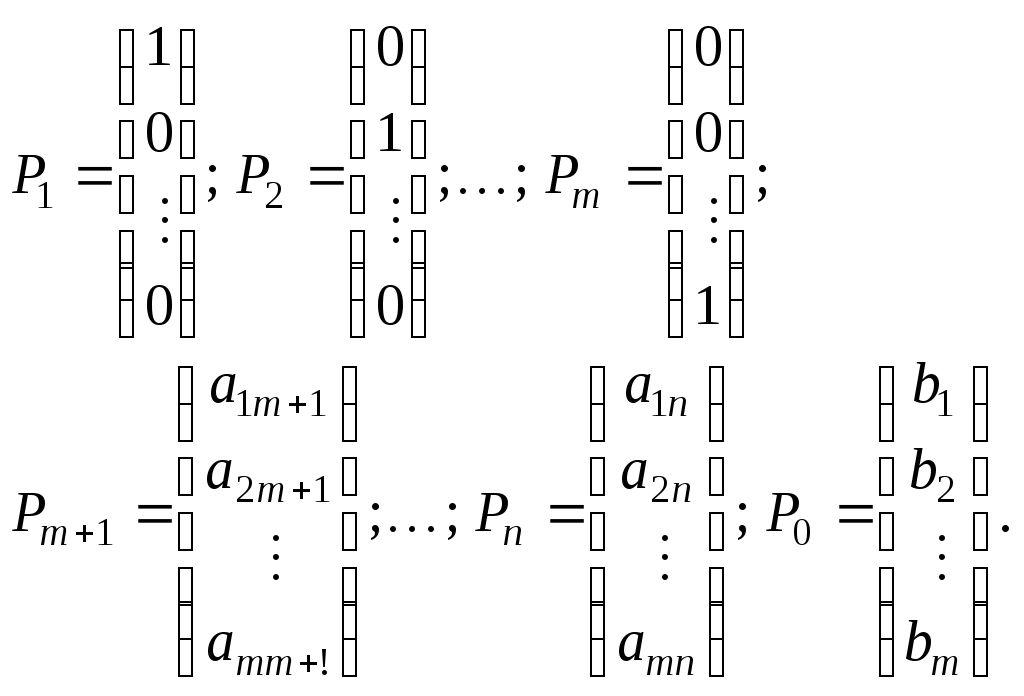
Так как
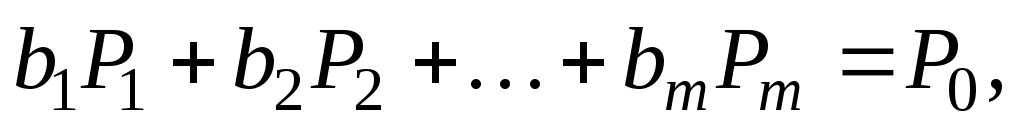
то по определению опорного плана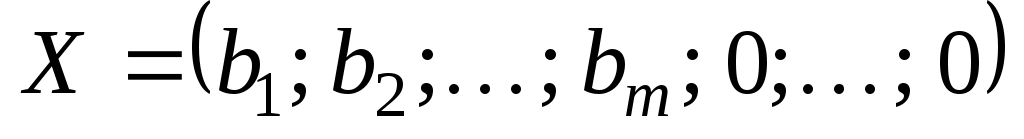 является опорным планом данной задачи (последние
является опорным планом данной задачи (последние 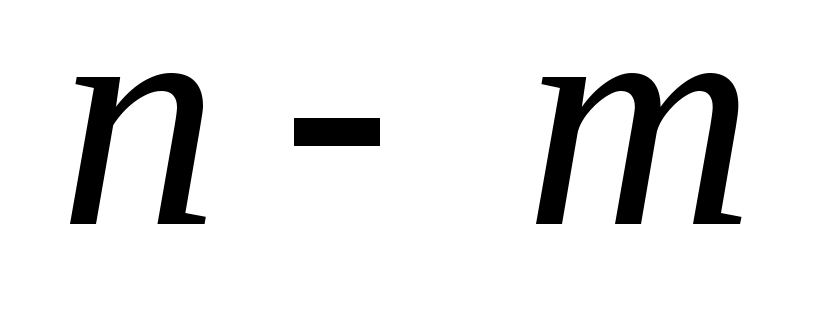 компонент вектора Х равны нулю). Этот план определяется системой единичных векторов
компонент вектора Х равны нулю). Этот план определяется системой единичных векторов 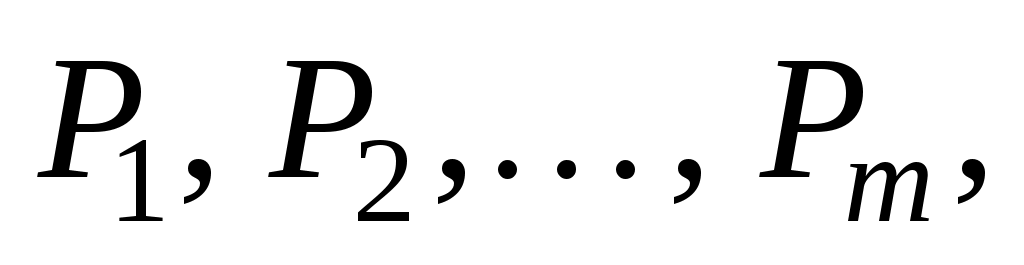 которые образуют базис
которые образуют базис
m-мерного пространства. Поэтому каждый из векторов а также вектор
а также вектор  могут быть представлены в виде линейной комбинации векторов данного базиса. Пусть
могут быть представлены в виде линейной комбинации векторов данного базиса. Пусть
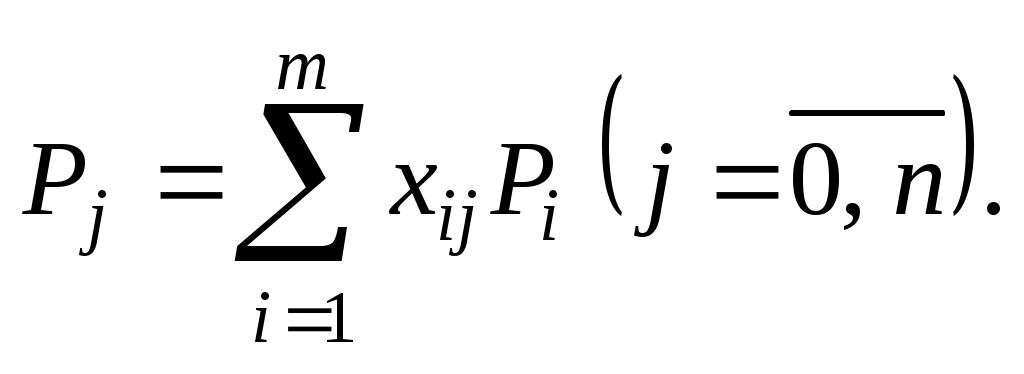
Положим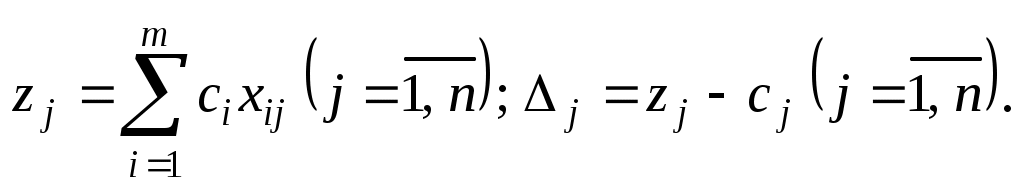 Так как векторы
Так как векторы 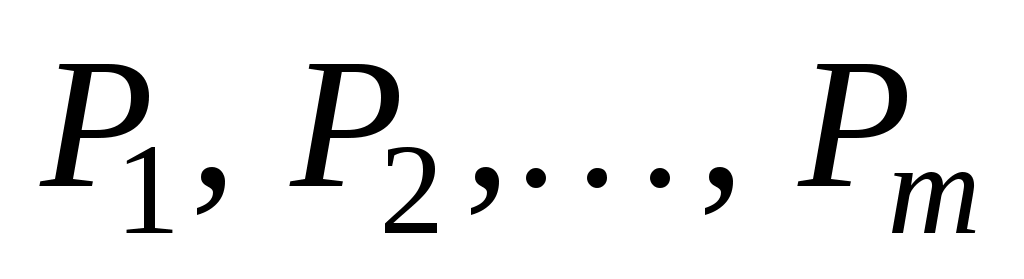 — единичные, то
— единичные, то 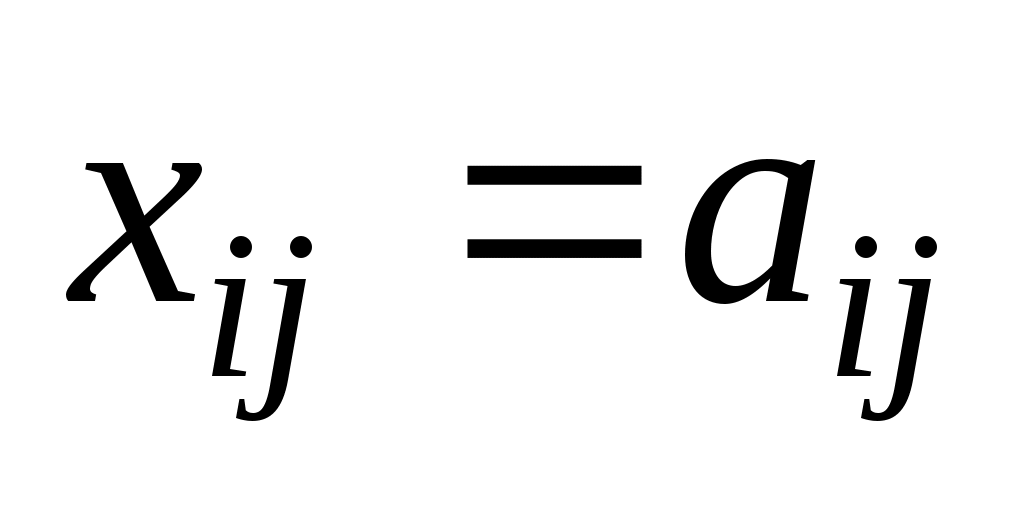 и
и 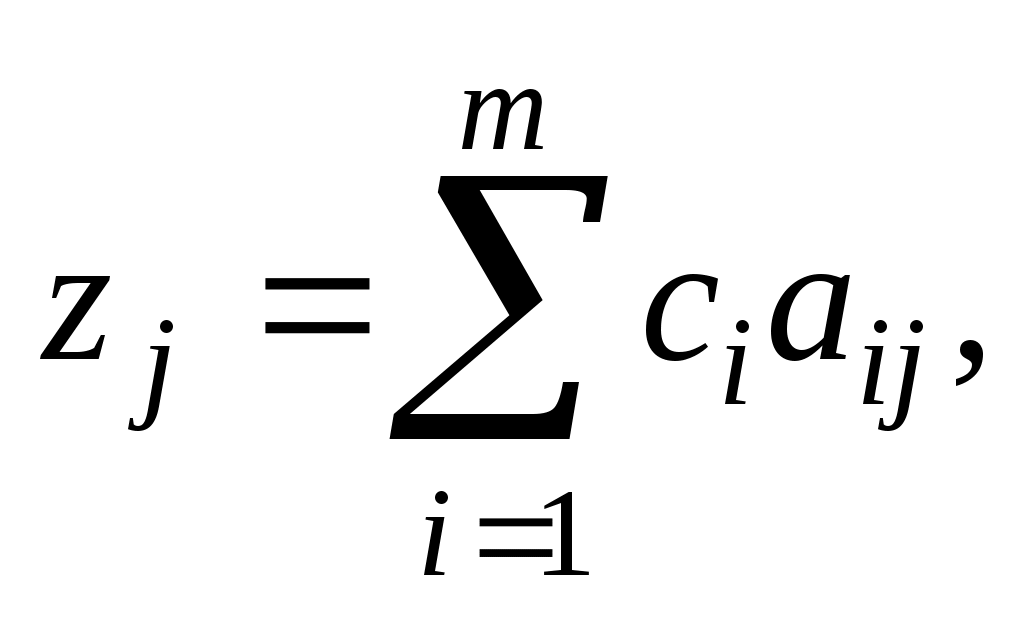 а
а
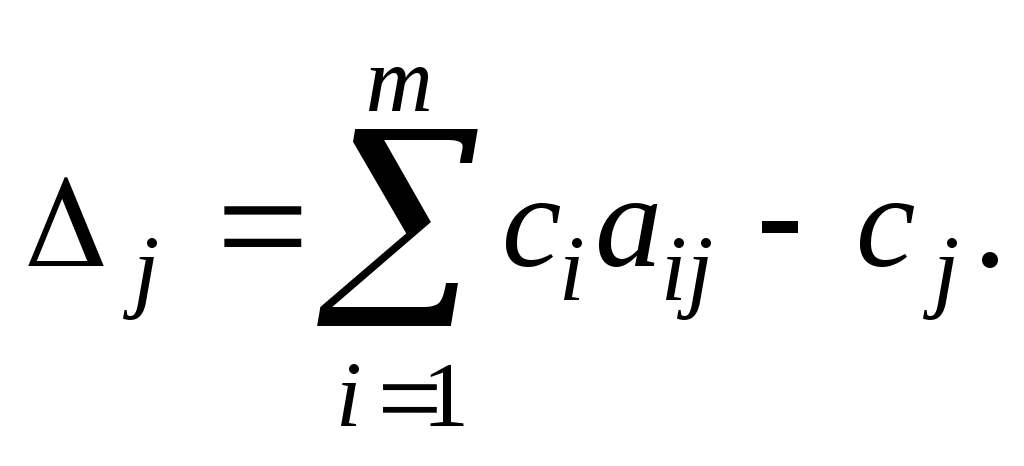
Теорема__1.6.'>Теорема__1.5'>Теорема 1.5 (признак оптимальности опорного плана). Опорный план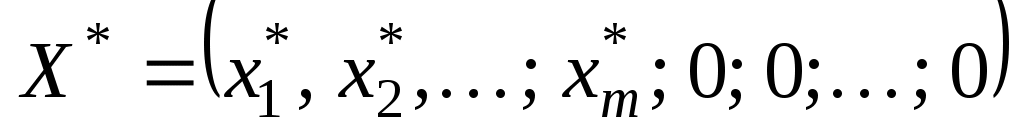 задачи (22)-(24) является оптимальным, если
задачи (22)-(24) является оптимальным, если 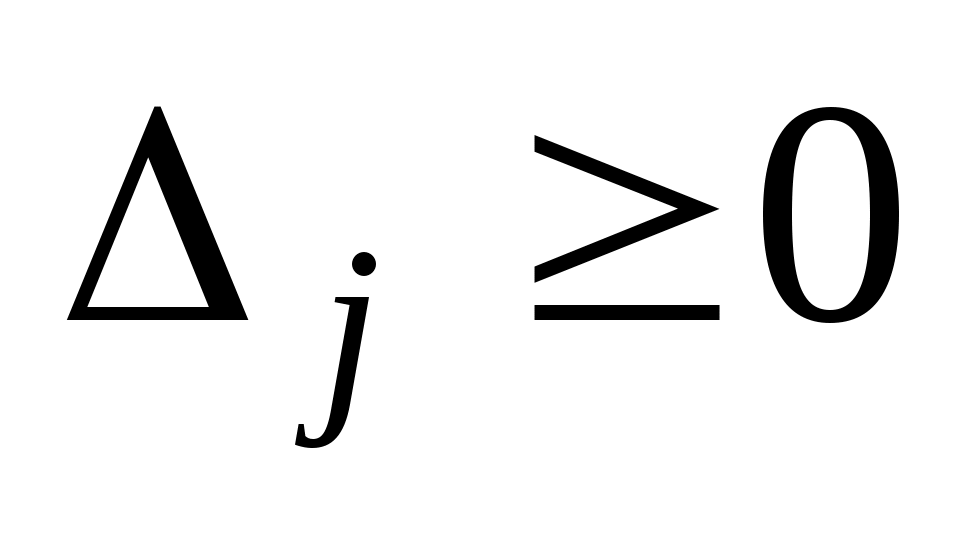 для любого j
для любого j 
Теорема 1.6. Если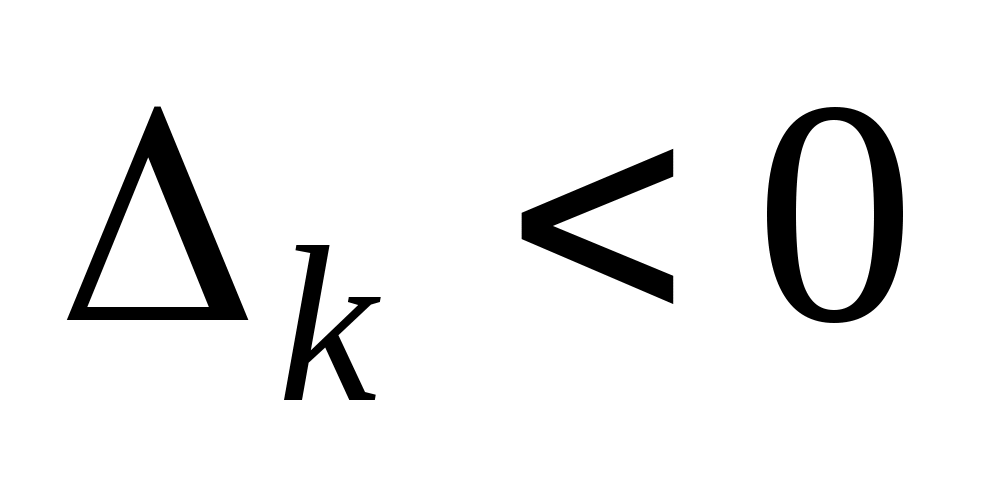 для некоторого j=k и среди чисел
для некоторого j=k и среди чисел 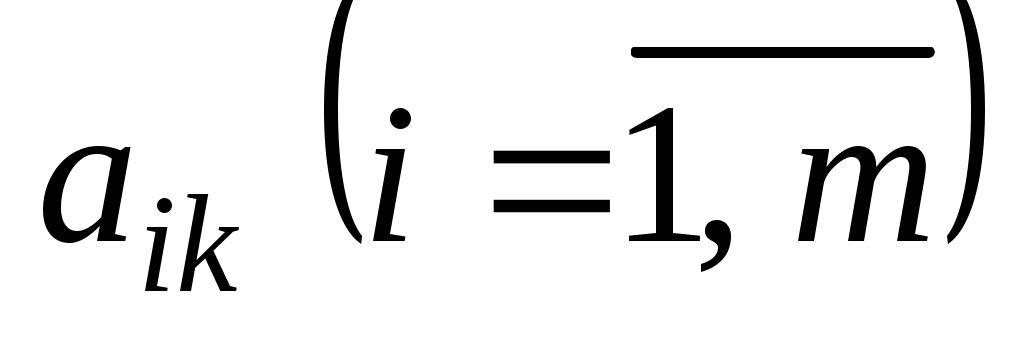 нет положительных
нет положительных 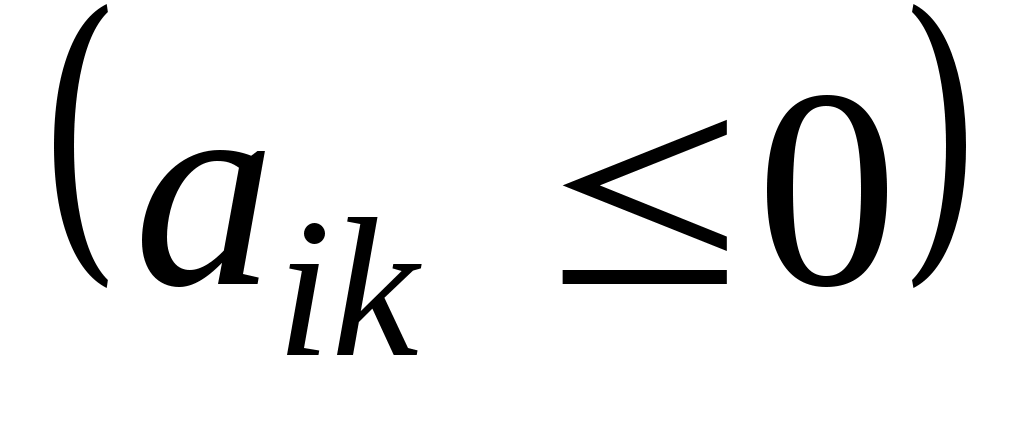 , то целевая функция (22) задачи (22)-(24) не ограничена на множестве ее планов.
, то целевая функция (22) задачи (22)-(24) не ограничена на множестве ее планов.
Теорема 1.7. Если опорный план Х задачи (22)-(24) не вырожден и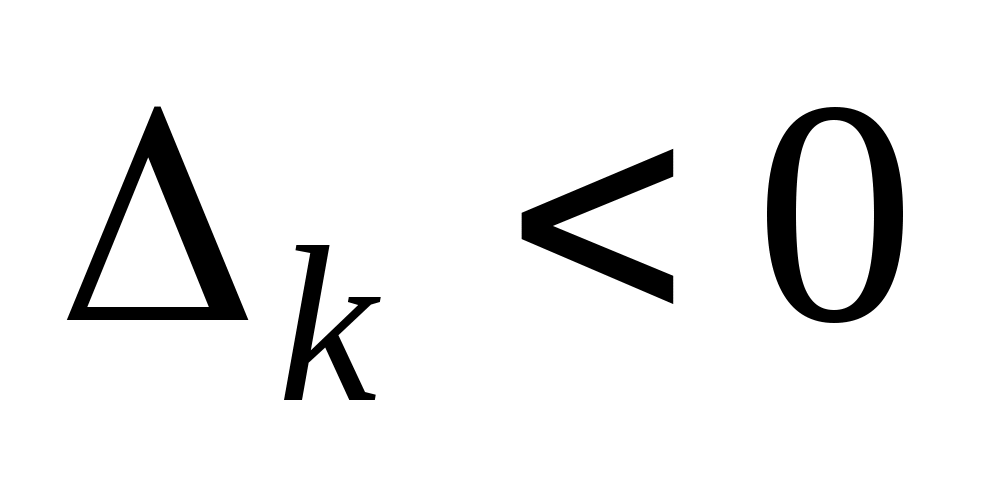 , но среди чисел аik есть положительные (не все
, но среди чисел аik есть положительные (не все 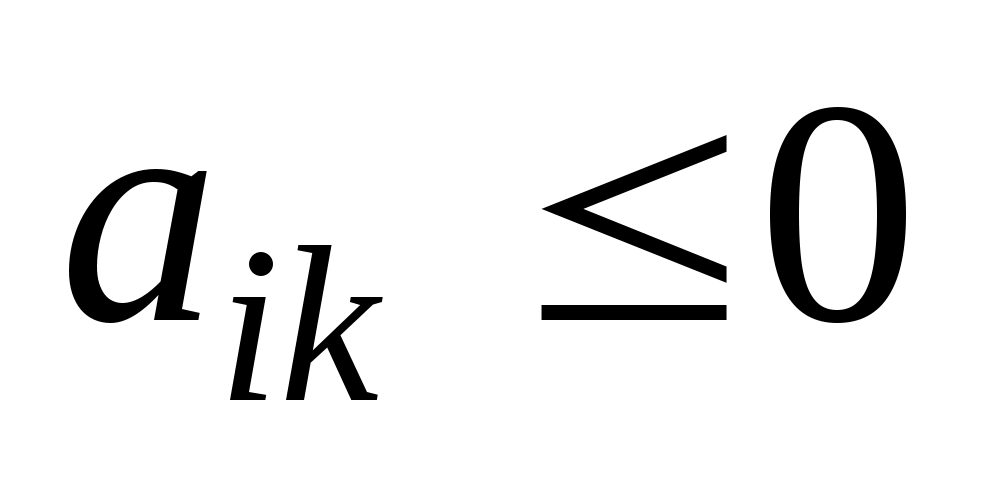 ), то существует опорный план X' такой, что
), то существует опорный план X' такой, что 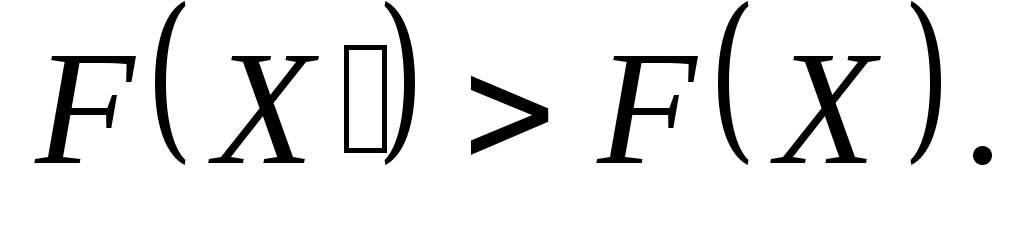
Сформулированные теоремы позволяют проверить

Рис. 5
Пересечение полученных полуплоскостей и определяет многоугольник решений данной задачи.
Как видно из рис. 5, многоугольником решений является пятиугольник OABCD. Координаты любой точки, принадлежащей этому пятиугольнику, удовлетворяют данной системе неравенств и условию неотрицательности переменных. Поэтому сформулированная задача будет решена, если мы сможем найти точку, принадлежащую пятиугольнику OABCD, в которой функция Fпринимает максимальное значение. Чтобы найти указанную точку, построим вектор
Если теперь взять какую-нибудь точку, принадлежащую построенной прямой и многоугольнику решений, то ее координаты определяют такой план производства изделий А и В, при котором прибыль от их реализации равна 480 руб. Далее, полагая h равным некоторому числу, большему чем 480, мы будем получать различные параллельные прямые. Если они имеют общие точки с многоугольником решений, то эти точки определяют планы производства изделий А и В, при которых прибыль от их реализации превзойдет 480 руб.
Перемещая построенную прямую
В. Координаты этой точки и определяют план выпуска изделий А и В, при котором прибыль от их реализации является максимальной.
Найдем координаты точки В как точки пересечения прямых II и III. Следовательно, ее координаты удовлетворяют уравнениям этих прямых
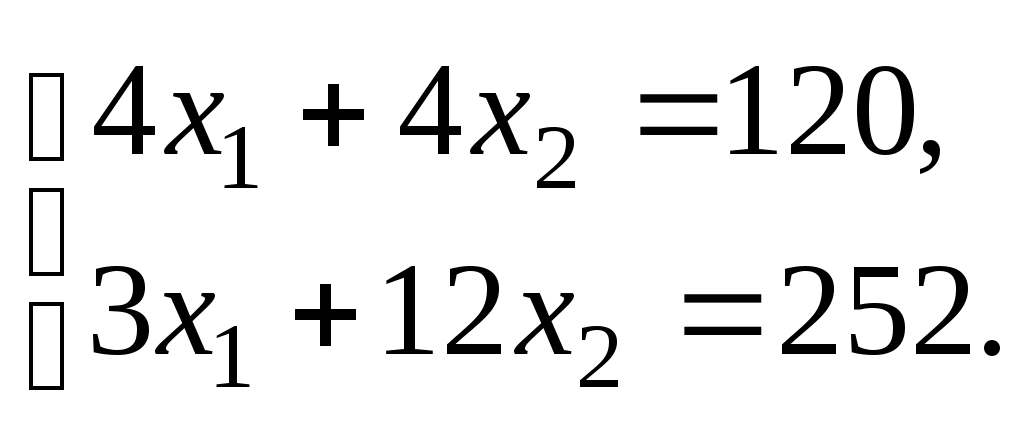
Решив эту систему уравнений, получим
1.7. Найти максимум и минимум функции
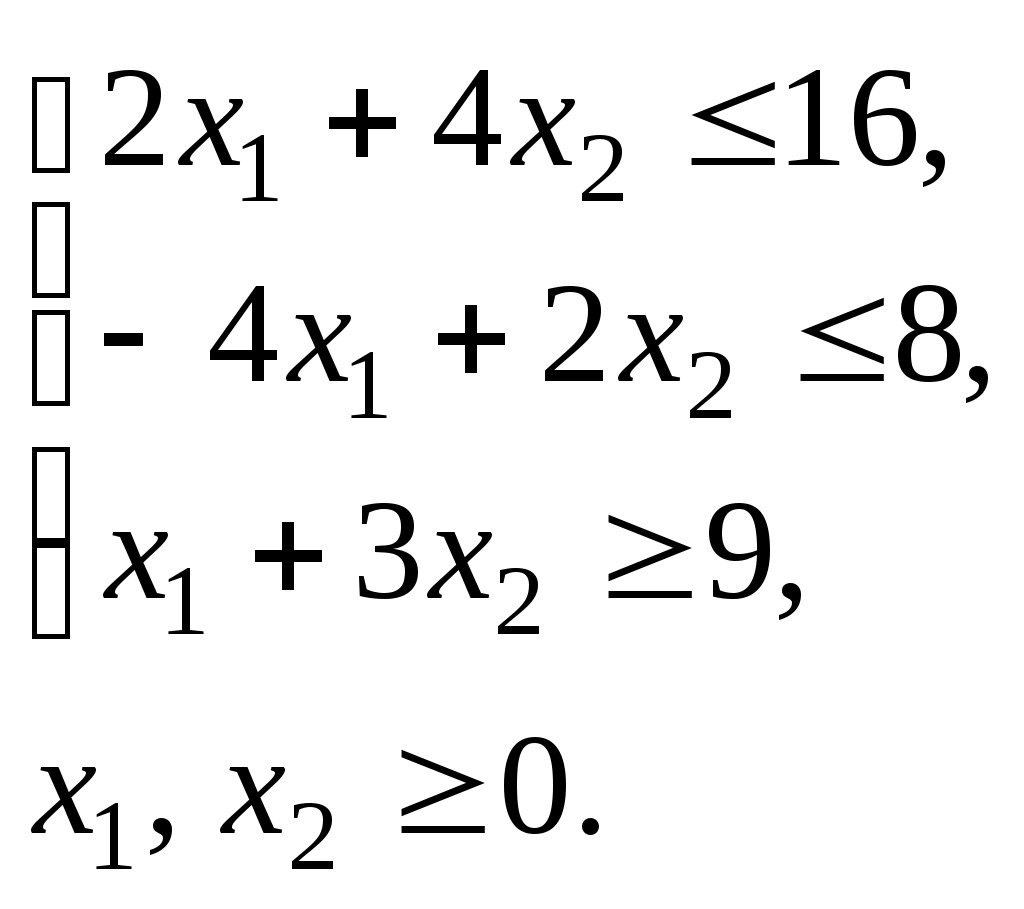
Решение. Построим многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств:

Построив полученные прямые, найдем соответствующие полуплоскости и их пересечение (рис. 6).
Как видно из рис. 6, многоугольником решений задачи является треугольник АВС. Координаты точек этого треугольника удовлетворяют условию неотрицательности и неравенствам системы ограничений задачи. Следовательно, задача будет решена, если среди точек треугольника АВС найти такие, в которых функция
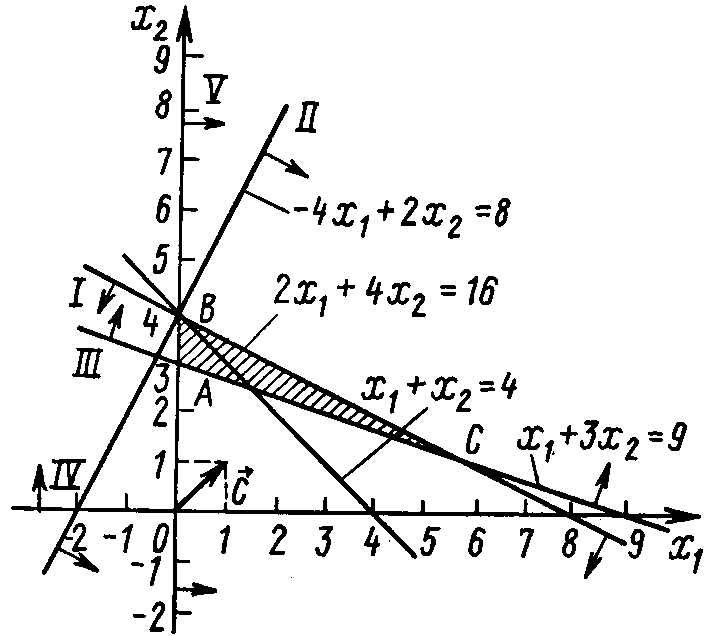
Рис. 6
Передвигая данную прямую параллельно самой себе в направлении вектора
Следовательно, в этой точке функция F принимает максимальное значение. Так как С — точка пересечения прямых I и II, то ее координаты удовлетворяют уравнениям этих прямых:
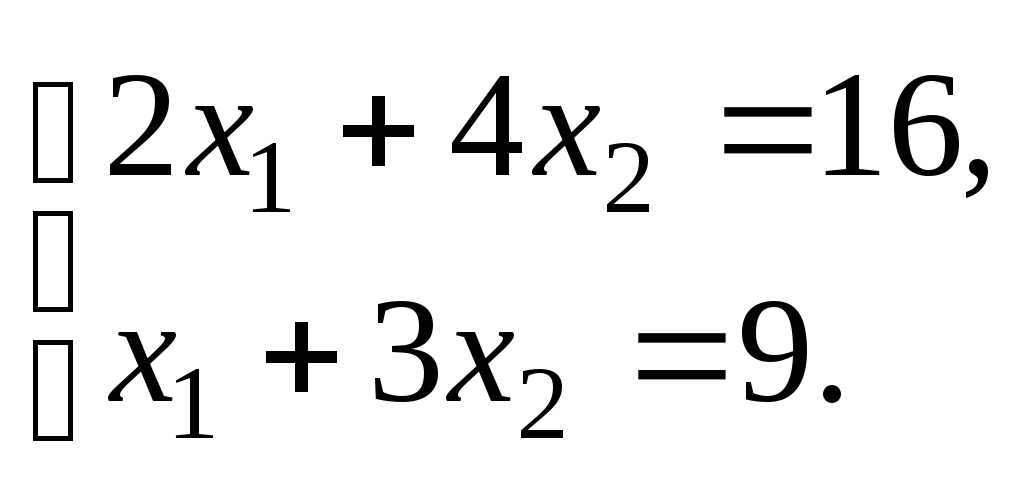
Решив эту систему уравнений, получим
Для нахождения минимального значения целевой функции задачи передвигаем прямую

откуда
1.5. Симплекс метод
Решение любой задачи линейного программирования можно найти симплексным методом. Прежде чем применять указанный метод, следует записать исходную задачу в форме основной задачи линейного программирования, если она не имеет такой формы записи.
Симплексный метод решения задачи линейного программирования основан на пеереходе от одного опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план и каждый ее опорный план является невырожденным). Указанный переход возможен, если известен какой-нибудь исходный опорный план. Рассмотрим задачу, для которой этот план можно непосредственно записать.
Пусть требуется найти максимальное значение функции
при условиях
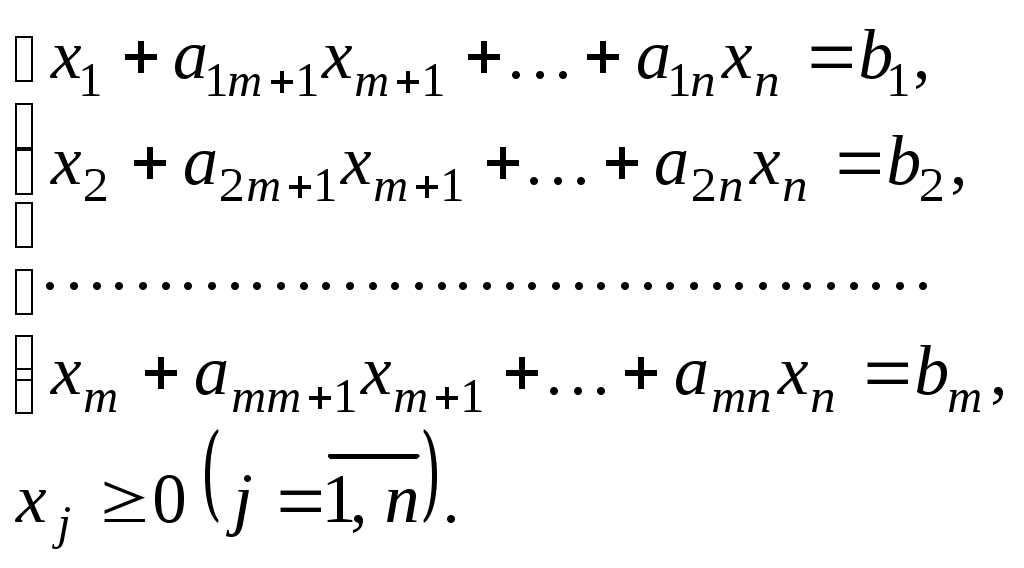
Здесь
Векторная форма данной задачи имеет следующий вид: найти максимум функции
при условиях
где
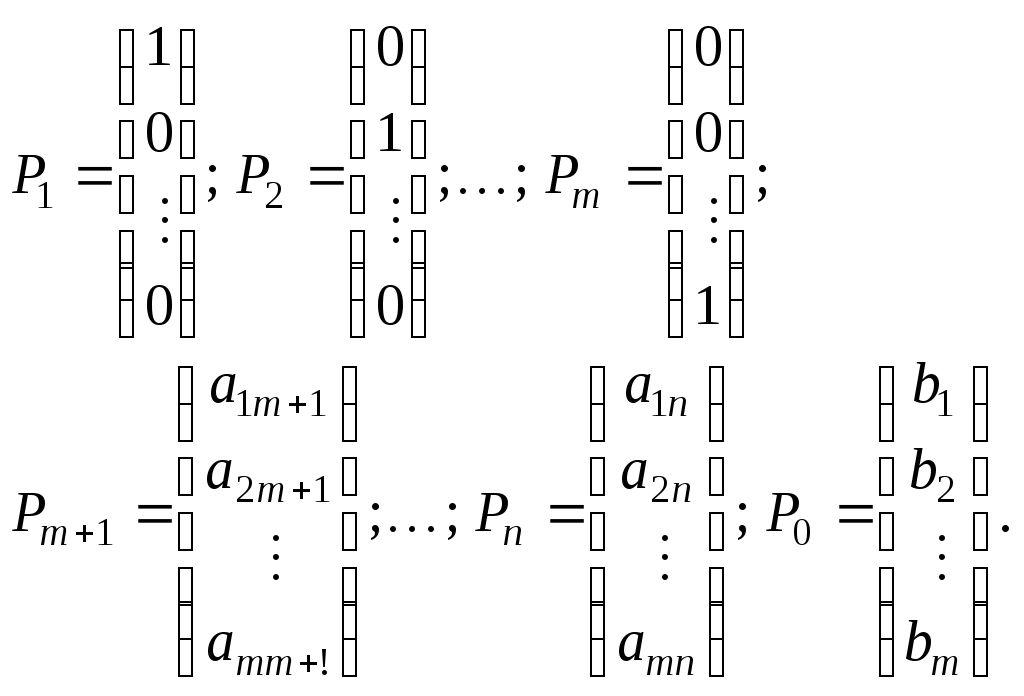
Так как
то по определению опорного плана
m-мерного пространства. Поэтому каждый из векторов
Положим
Теорема__1.6.'>Теорема__1.5'>Теорема 1.5 (признак оптимальности опорного плана). Опорный план
Теорема 1.6. Если
Теорема 1.7. Если опорный план Х задачи (22)-(24) не вырожден и
Сформулированные теоремы позволяют проверить