Файл: Методическое пособие по дисциплине методы оптимальных решений 1 семестр Направление подготовки 080100 Экономика.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 173
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, является ли найденный опорный план оптимальным, и выявить целесообразность перехода к новому опорному плану.
Исследование опорного плана на оптимальность, а также дальнейший вычислительный процесс удобнее вести, если условия задачи и первоначальные данные, полученные после определения исходного опорного плана, записать так, как показано в таблице 3.
В столбце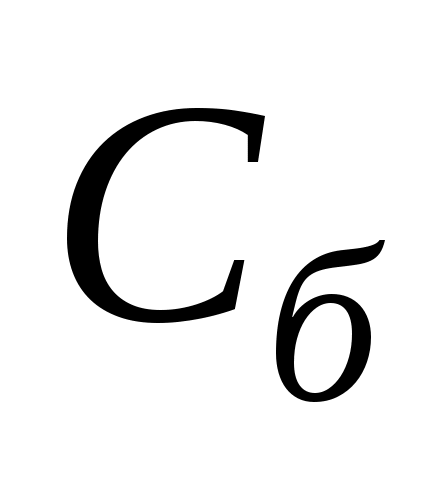 этой таблицы записывают коэффициенты при неизвестных целевой функции, имеющие те же индексы, что и векторы данного базиса.
этой таблицы записывают коэффициенты при неизвестных целевой функции, имеющие те же индексы, что и векторы данного базиса.
В столбце записывают положительные компоненты исходного опорного плана, в нем же в результате вычислений получают положительные компоненты оптимального плана. Столбцы векторов
записывают положительные компоненты исходного опорного плана, в нем же в результате вычислений получают положительные компоненты оптимального плана. Столбцы векторов  представляют собой коэффициенты разложения этих векторов по векторам данного базиса.
представляют собой коэффициенты разложения этих векторов по векторам данного базиса.
В таблице 3 первые m строк определяются исходными данными задачи, а показатели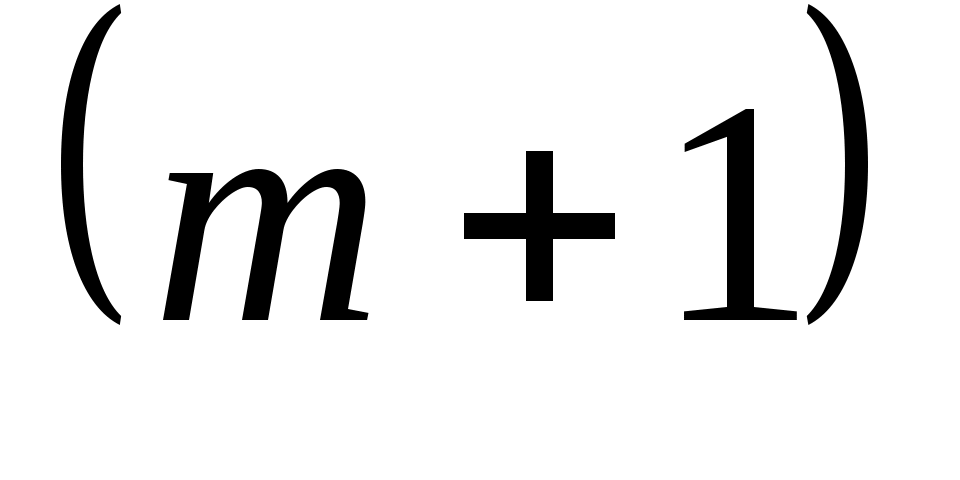 -й строки вычисляют. В этой строке в столбце вектора
-й строки вычисляют. В этой строке в столбце вектора  записывают значение целевой функции, которое она принимает при данном опорном плане, а в столбце вектора
записывают значение целевой функции, которое она принимает при данном опорном плане, а в столбце вектора  — значение
— значение 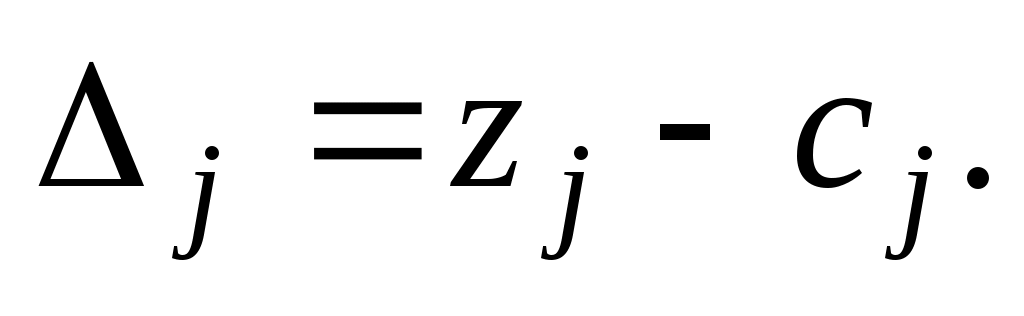
Значение находится как скалярное произведение вектора
находится как скалярное произведение вектора 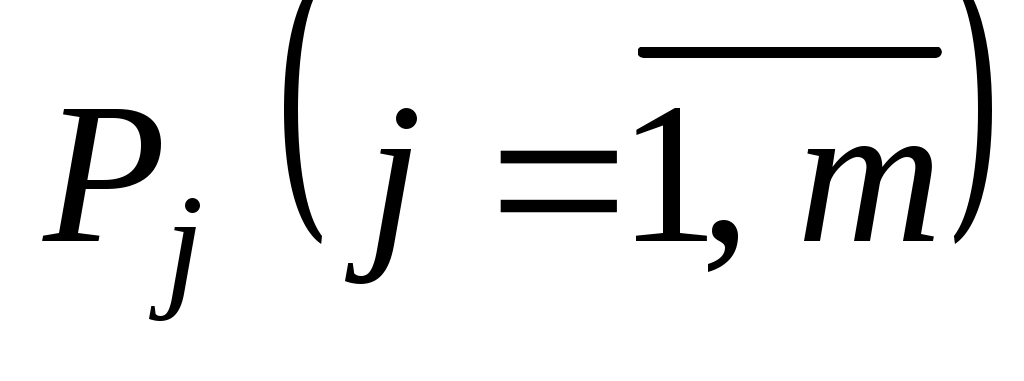 на вектор
на вектор 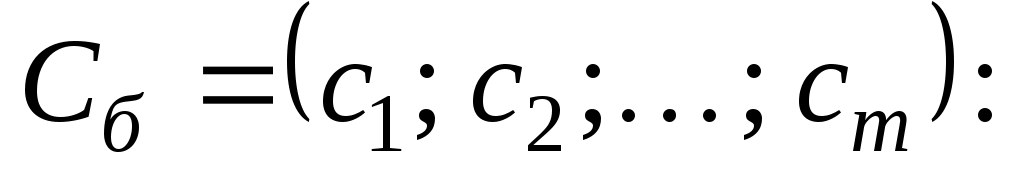
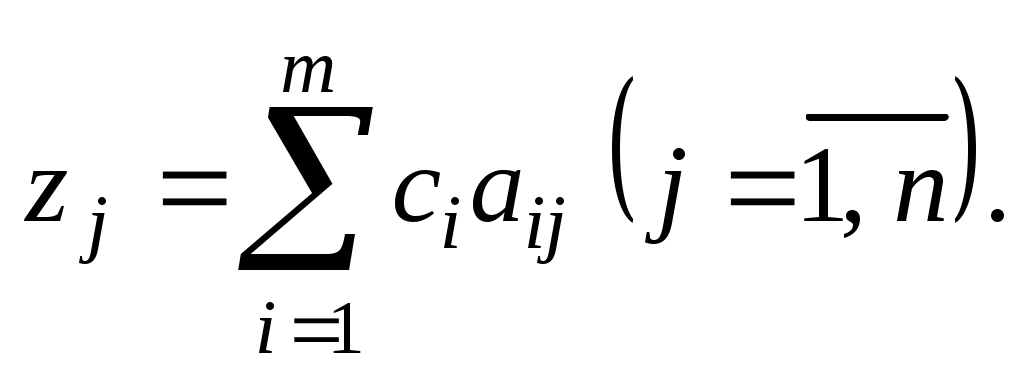
Значение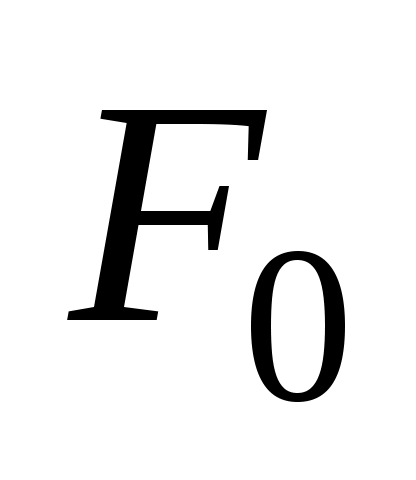 равно скалярному произведению вектора
равно скалярному произведению вектора  на вектор
на вектор 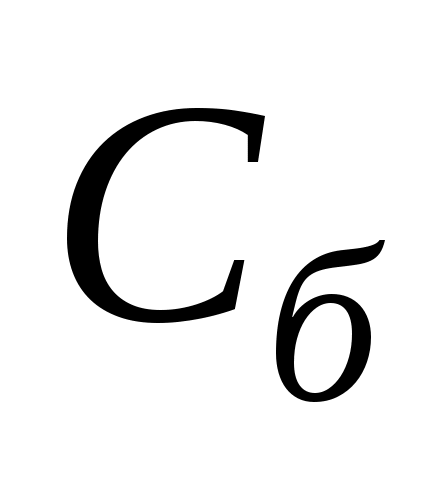 :
:
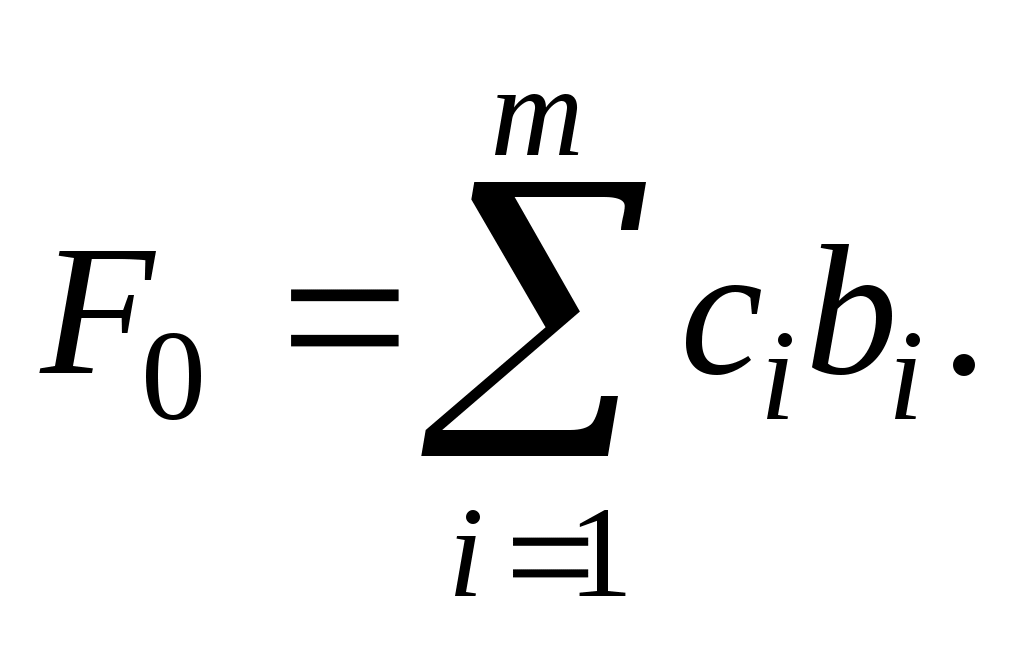
После заполнения таблицы 3 исходный опорный план проверяют на оптимальность. Для этого просматривают элементы -й строки таблицы. В результате может иметь место один из следующих трех случаев:
-й строки таблицы. В результате может иметь место один из следующих трех случаев:
1) для
для 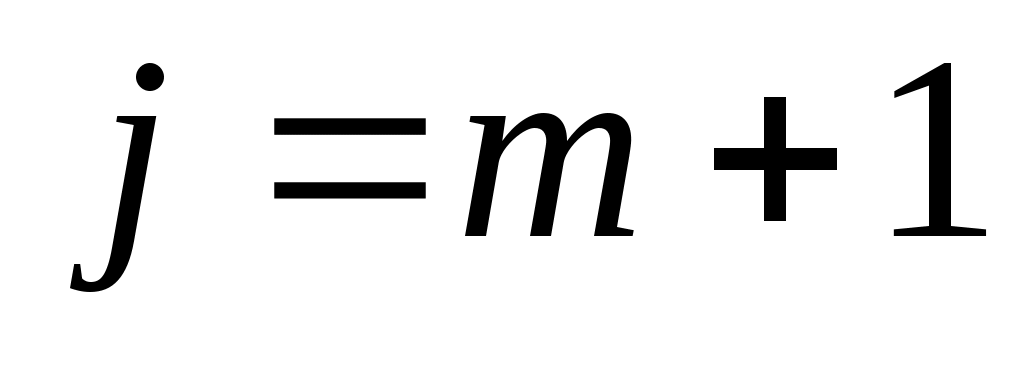 ,
, 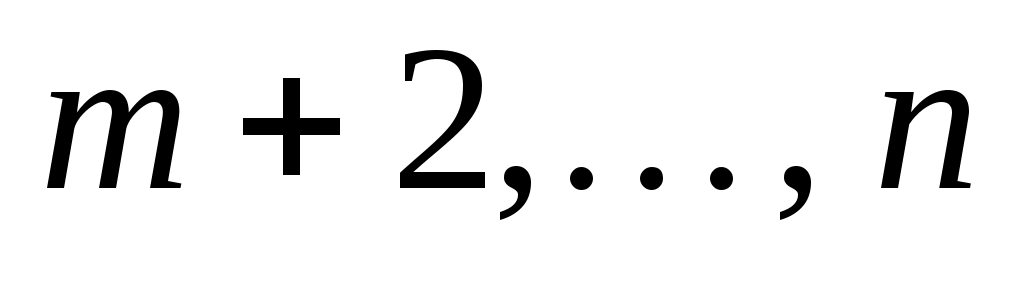 (при
(при 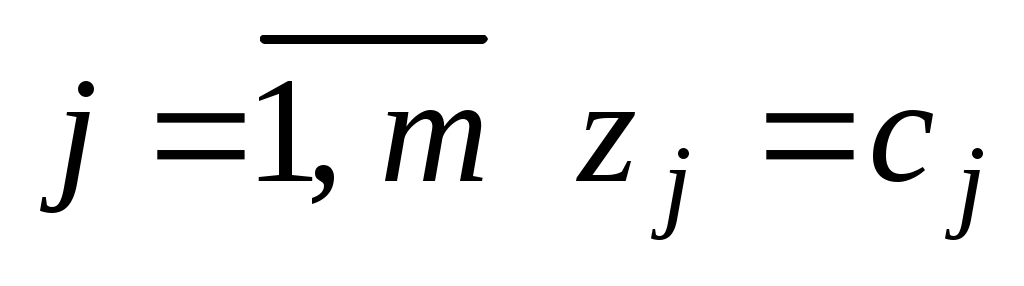 ). Поэтому в данном случае числа
). Поэтому в данном случае числа  для всех j от 1 до n;
для всех j от 1 до n;
2)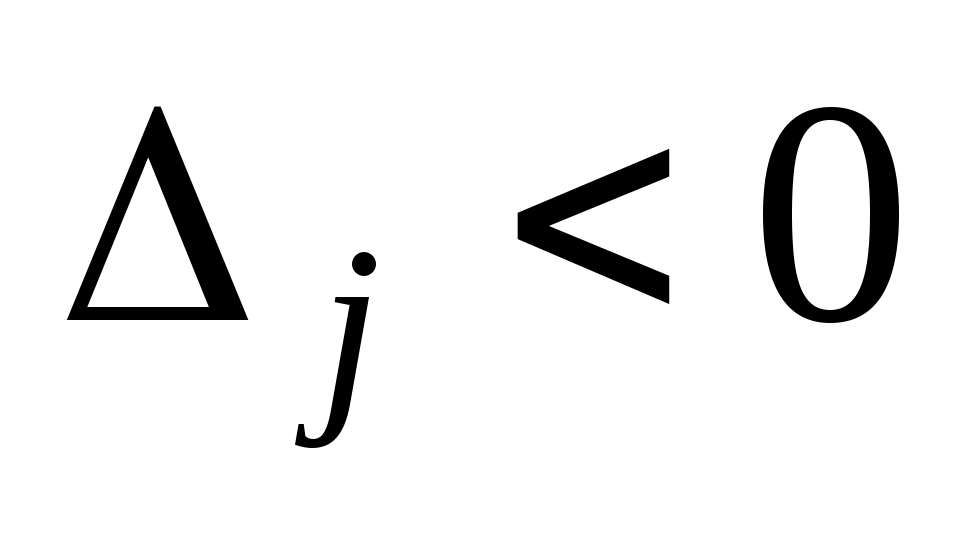 для некоторого j, и все соответствующие этому индексу величины
для некоторого j, и все соответствующие этому индексу величины 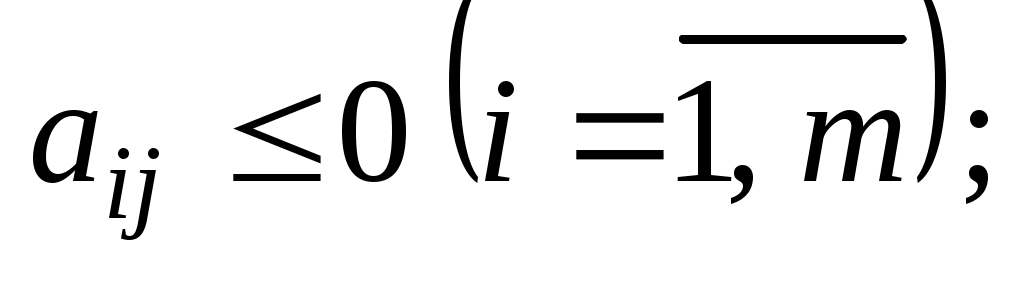
3)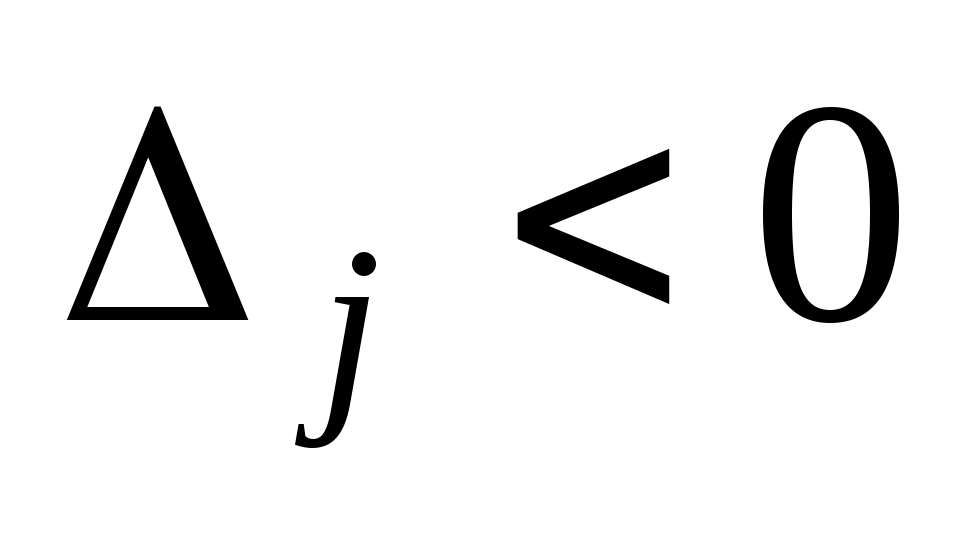 для некоторых индексов j, и для каждого такого j, по крайней мере, одно из чисел
для некоторых индексов j, и для каждого такого j, по крайней мере, одно из чисел  положительно.
положительно.
Таблица 3
В первом случае на основании признака оптимальности исходный опорный план является оптимальным. Во втором случае целевая функция не ограничена сверху на множестве планов, а в третьем случае можно перейти от исходного плана к новому опорному плану, при котором значение целевой функции увеличится. Этот переход от одного опорного плана к другому осуществляется исключением из исходного базиса какого-нибудь из векторов и введением в него нового вектора. В качестве вектора, вводимого в базис, можно взять любой из векторов имеющий индекс j, для которого
имеющий индекс j, для которого  . Пусть, например,
. Пусть, например, 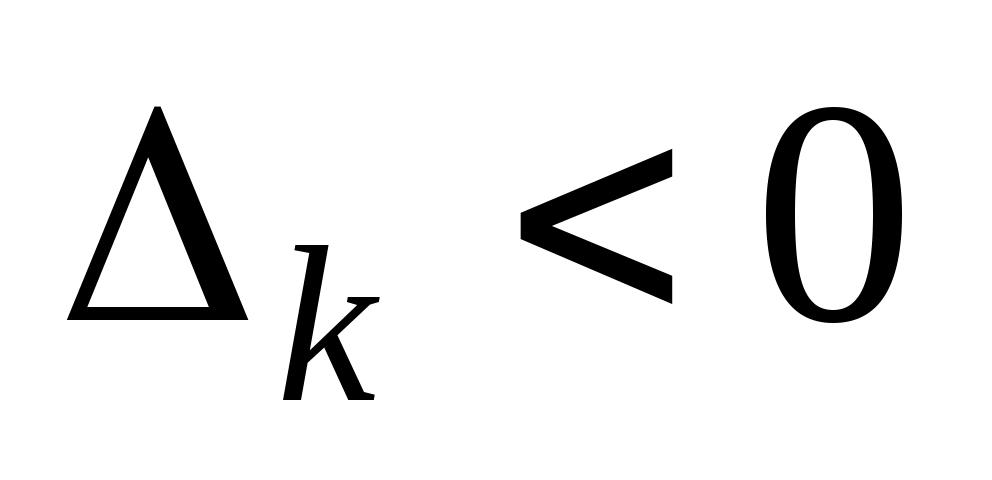 и решено ввести в базис вектор
и решено ввести в базис вектор 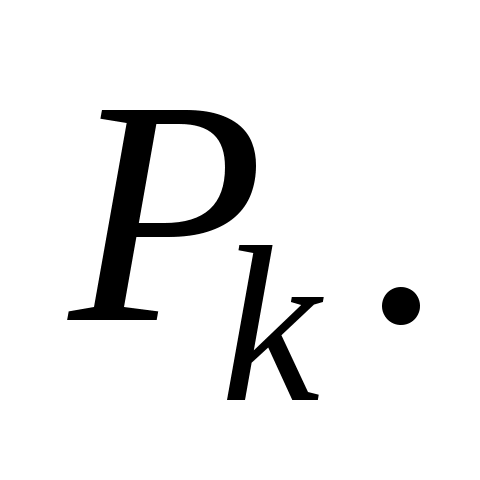
Для определения вектора, подлежащего исключению из базиса, находят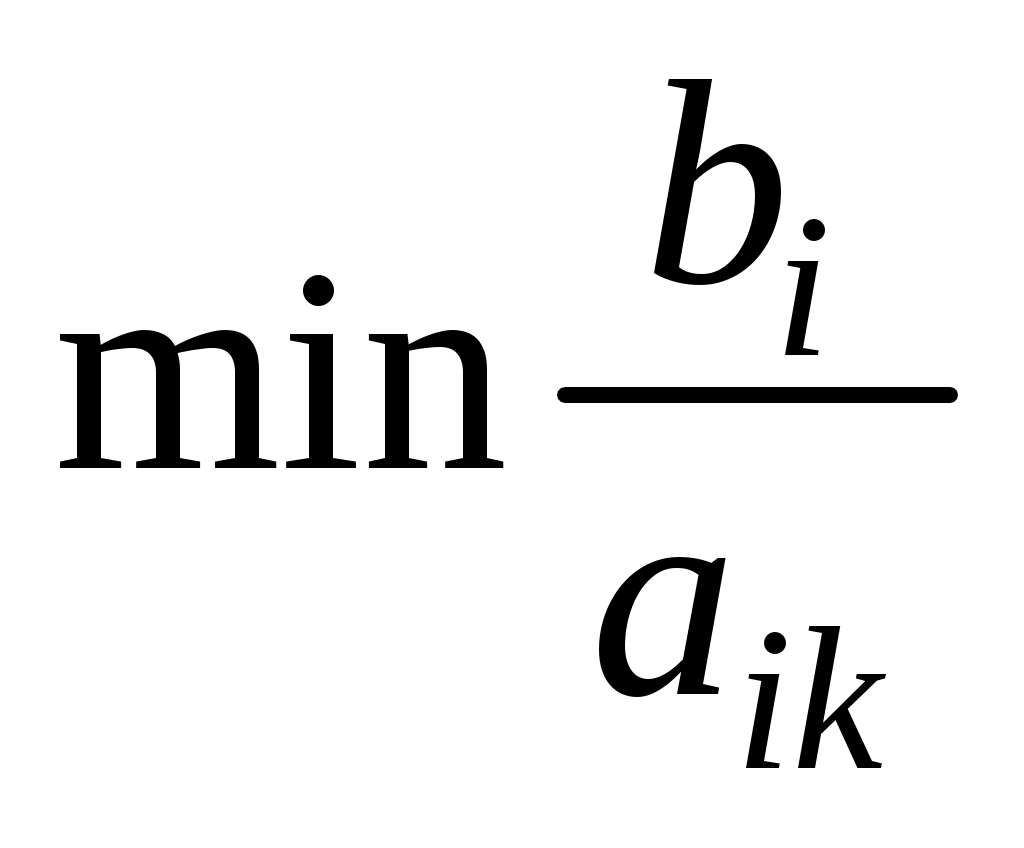 для всех
для всех 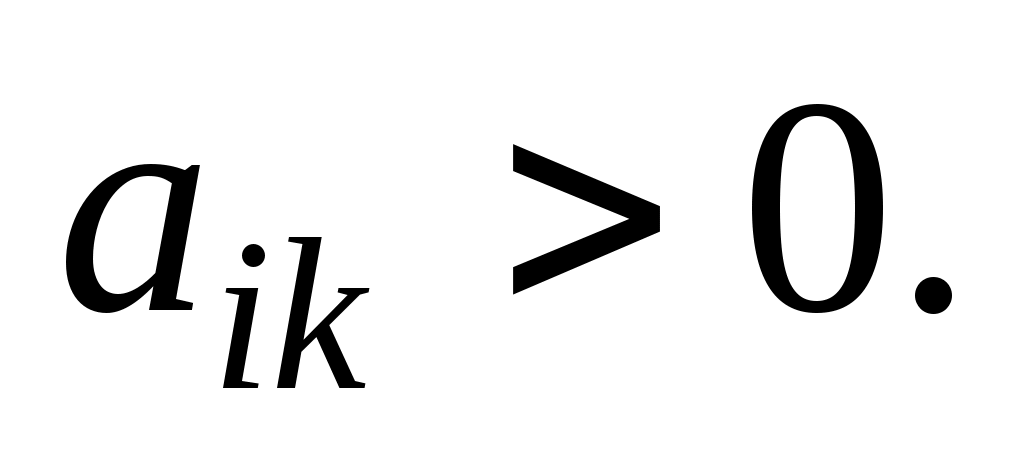 Пусть этот минимум достигается при i=r. Тогда из базиса исключают вектор
Пусть этот минимум достигается при i=r. Тогда из базиса исключают вектор 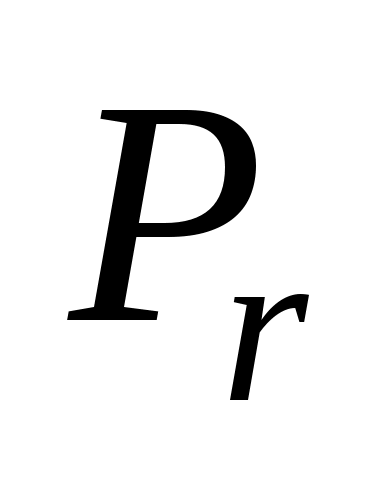 ,а число
,а число 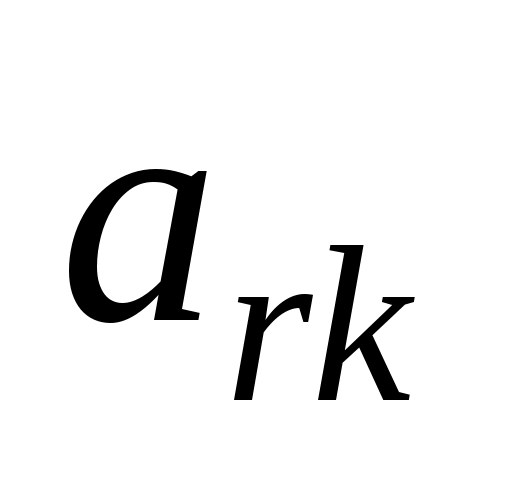 называют разрешающим элементом.
называют разрешающим элементом.
Столбец и строку, на пересечении которых находится разрешающий элемент, называют направляющими.
После выделения направляющей строки и направляющего столбца находят новый опорный план и коэффициенты разложения векторов через векторы нового базиса, соответствующего новому опорному плану. Это легко реализовать, если воспользоваться методом Жордана—Гаусса. При этом можно показать, что положительные компоненты нового опорного плана вычисляются по формулам
через векторы нового базиса, соответствующего новому опорному плану. Это легко реализовать, если воспользоваться методом Жордана—Гаусса. При этом можно показать, что положительные компоненты нового опорного плана вычисляются по формулам
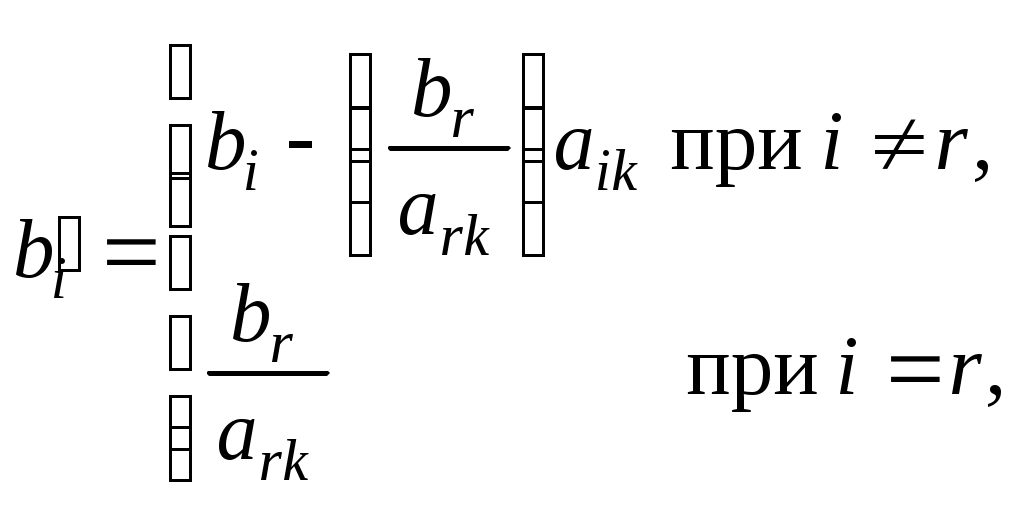 (25)
(25)
а коэффициенты разложения векторов через векторы нового базиса, соответствующего новому опорному плану, — по формулам
через векторы нового базиса, соответствующего новому опорному плану, — по формулам
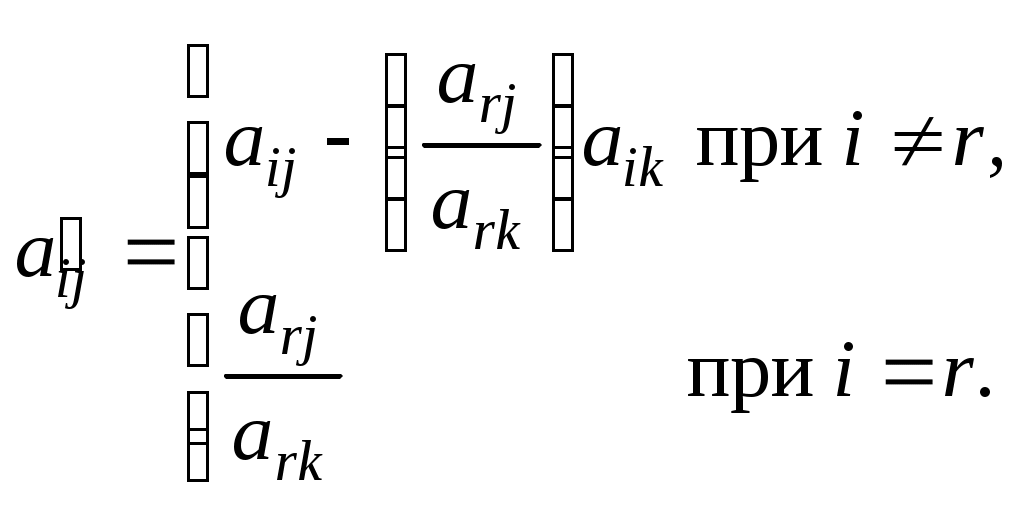
(26)
После вычисления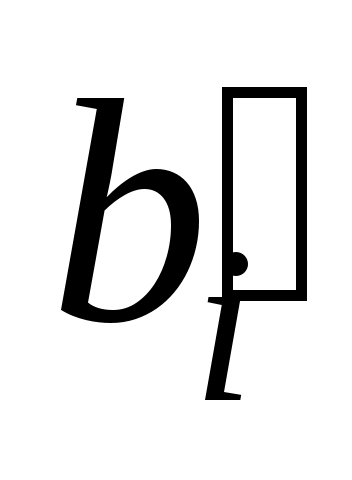 и
и  согласно формулам (25) и (26) их значения заносят в табл. 4.
согласно формулам (25) и (26) их значения заносят в табл. 4.
Таблица 4
Элементы -й строки этой таблицы могут быть вычислены либо по формулам
-й строки этой таблицы могут быть вычислены либо по формулам
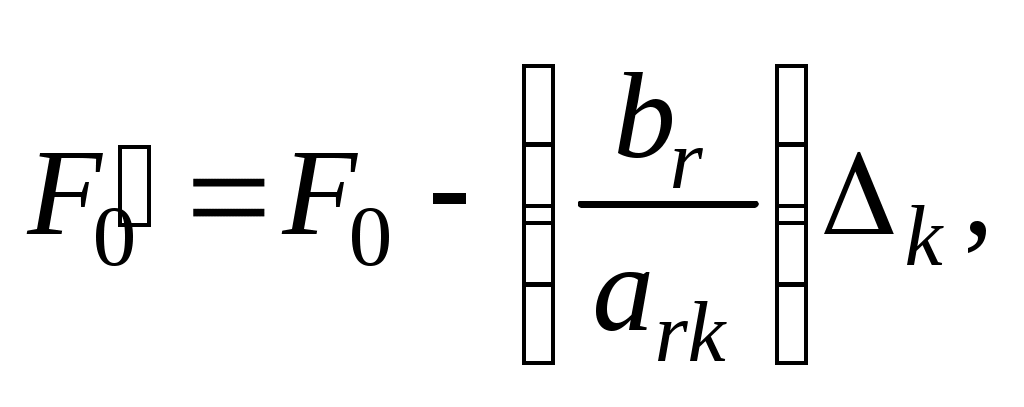 (27)
(27)
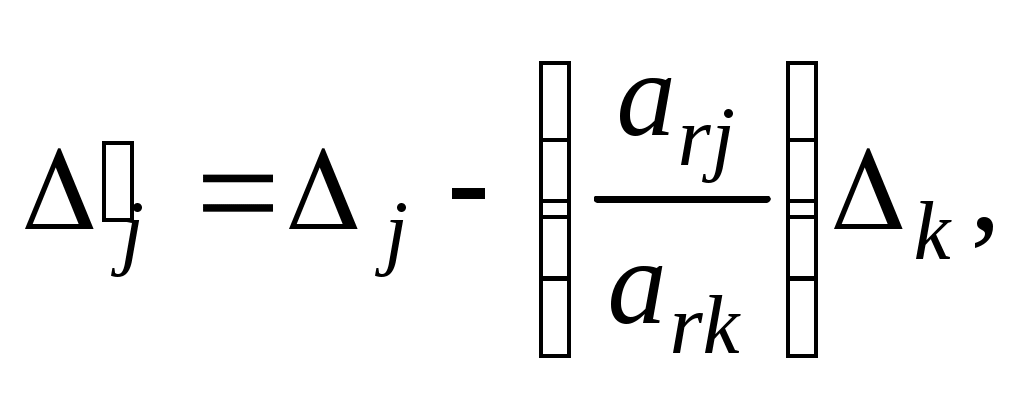 (28)
(28)
либо на основании их определения.
Наличие двух способов нахождения элементов -й строки позволяет осуществлять контроль правильности проводимых вычислений.
-й строки позволяет осуществлять контроль правильности проводимых вычислений.
Из формулы (27) следует, что при переходе от одного опорного плана к другому наиболее целесообразно ввести в базис вектор , имеющий индекс j, при котором максимальным по абсолютной величине является число
, имеющий индекс j, при котором максимальным по абсолютной величине является число 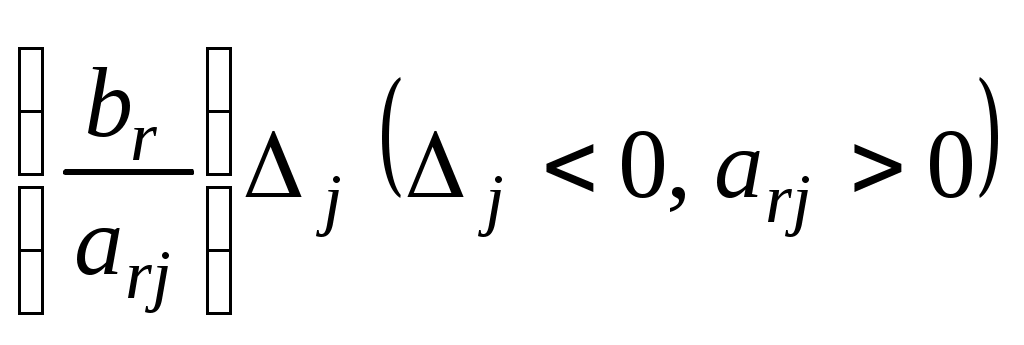 . Однако с целью упрощения вычислительного процесса в дальнейшем будем вектор, вводимый в базис, определять, исходя из максимальной абсолютной величины отрицательных чисел
. Однако с целью упрощения вычислительного процесса в дальнейшем будем вектор, вводимый в базис, определять, исходя из максимальной абсолютной величины отрицательных чисел  . Если же таких чисел несколько, то в базис будем вводить вектор, имеющий такой же индекс, как и максимальное из чисел
. Если же таких чисел несколько, то в базис будем вводить вектор, имеющий такой же индекс, как и максимальное из чисел  , определяемых данными числами
, определяемых данными числами 
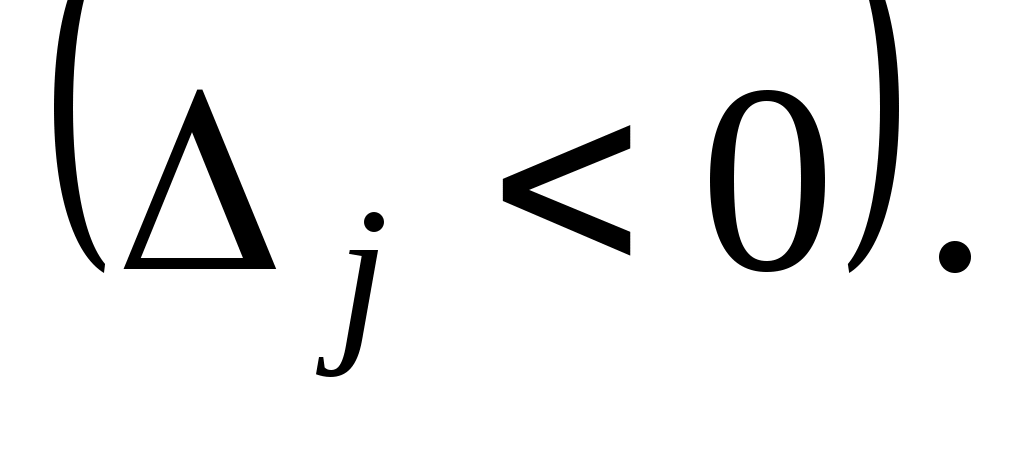
Итак, переход от одного опорного плана к другому сводится к переходу от одной симплекс-таблицы к другой. Элементы новой симплекс-таблицы можно вычислить как с помощью рекуррентных формул (25)-(28), так и по правилам, непосредственно вытекающим из них. Эти правила состоят в следующем.
В столбцах векторов, входящих в базис, на пересечении строк и столбцов одноименных векторов проставляются единицы, а все остальные элементы данных столбцов полагают равными нулю.
Элементы векторов и
и  в строке новой симплекс-таблицы, в которой записан вектор, вводимый в базис, получают из элементов этой же строки исходной таблицы делением их на величину разрешающего элемента. В столбце
в строке новой симплекс-таблицы, в которой записан вектор, вводимый в базис, получают из элементов этой же строки исходной таблицы делением их на величину разрешающего элемента. В столбце
Исследование опорного плана на оптимальность, а также дальнейший вычислительный процесс удобнее вести, если условия задачи и первоначальные данные, полученные после определения исходного опорного плана, записать так, как показано в таблице 3.
В столбце
В столбце
В таблице 3 первые m строк определяются исходными данными задачи, а показатели
Значение
Значение
После заполнения таблицы 3 исходный опорный план проверяют на оптимальность. Для этого просматривают элементы
1)
2)
3)
Таблица 3
| i | Базис | | P0 | | | ... | | ... | | | ... | | ... | |
| | | ... | | ... | | | ... | | ... | | ||||
| | | | | | | | | | | | | | | |
| | | | | 0 | 0 | ... | 0 | ... | 0 | | ... | | ... | |
В первом случае на основании признака оптимальности исходный опорный план является оптимальным. Во втором случае целевая функция не ограничена сверху на множестве планов, а в третьем случае можно перейти от исходного плана к новому опорному плану, при котором значение целевой функции увеличится. Этот переход от одного опорного плана к другому осуществляется исключением из исходного базиса какого-нибудь из векторов и введением в него нового вектора. В качестве вектора, вводимого в базис, можно взять любой из векторов
Для определения вектора, подлежащего исключению из базиса, находят
Столбец и строку, на пересечении которых находится разрешающий элемент, называют направляющими.
После выделения направляющей строки и направляющего столбца находят новый опорный план и коэффициенты разложения векторов
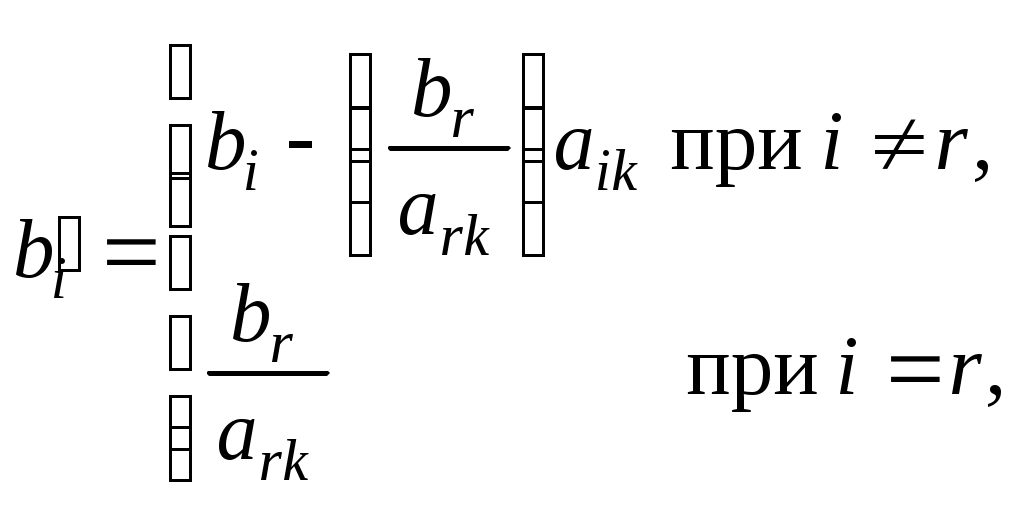 (25)
(25)а коэффициенты разложения векторов
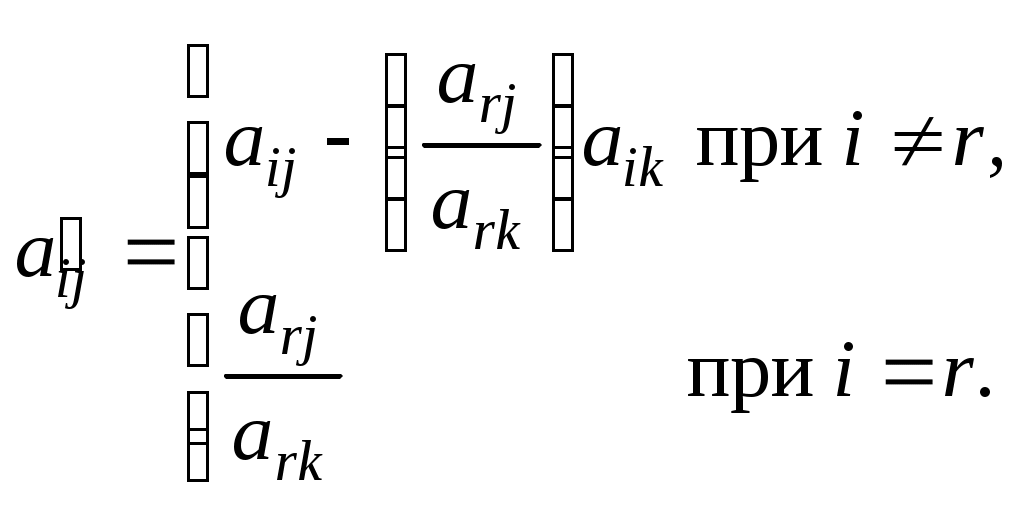
(26)
После вычисления
Таблица 4
| i | Базис | | P0 | | | ... | | ... | | | ... | | ... | |
| | | ... | | ... | | | ... | | ... | | ||||
| | | | | | | | | | | | | | | |
| | | | | 0 | 0 | ... | | ... | 0 | | ... | 0 | ... | |
Элементы
либо на основании их определения.
Наличие двух способов нахождения элементов
Из формулы (27) следует, что при переходе от одного опорного плана к другому наиболее целесообразно ввести в базис вектор
Итак, переход от одного опорного плана к другому сводится к переходу от одной симплекс-таблицы к другой. Элементы новой симплекс-таблицы можно вычислить как с помощью рекуррентных формул (25)-(28), так и по правилам, непосредственно вытекающим из них. Эти правила состоят в следующем.
В столбцах векторов, входящих в базис, на пересечении строк и столбцов одноименных векторов проставляются единицы, а все остальные элементы данных столбцов полагают равными нулю.
Элементы векторов