Файл: Динамическая линейная сочимодель распределения ресурсов в маркетинговых сетях безразличный Центр.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 34
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
,при условии 
, получаем
.
Таким образом, в те моменты времени
, когда
,
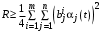оптимальным управлением Центра является
, 
.
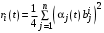В те же моменты времени , когда
,
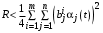оптимальным управлением Центра является
, .
Записывая оба выражения для
единой формулой, получаем оптимальное управление Центра:
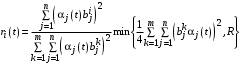, (36)
, ,
где
.
Зная вид управления (36), мы можем упростить (34), поскольку
,
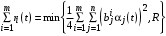а последнее слагаемое в (34)
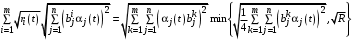
Приравнивая свободные члены в левой и правой частях уравнения (34), получаем дифференциальное уравнение для
:
,
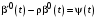где
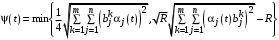, (37)т.е.
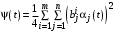, есл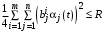и 
, и
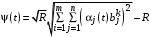, если 
.
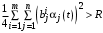Таким образом, уравнение (37) совпадает с уравнением (17) при тех же самых граничных условиях, следовательно
.
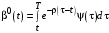При
имеем
,
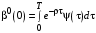где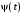
определяется выражением (37).
Таким образом, знаменатель выражения (20)
, т.е. глобальный максимум выигрыша Центра при кооперативном поведении, равен той же самой величине, что и правая часть выражения (19):
,
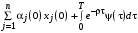где
, 
определяются формулой (6), а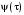 
, – выражением (18) или (37).
Индекс системной согласованности в нашей задаче оказался равным
,
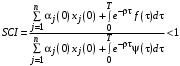хотя вычисления несколько различались, но ответ получался один и тот же.
Заметим, что системная согласованность возможна только в случае, когда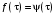
, а это возможно только в случае, когда для всех агентов влияния выполняется
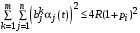
и им просто не хватает ресурсов на общие цели.
6. Случай благожелательного к агенту влияния Центра..
Перейдем теперь к задаче благожелательного к интересам агента влияния Центра:
,
, , , ,
, 
, 
,
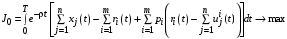Выпишем уравнение Гамильтона-Якоби-Беллмана:
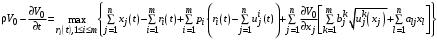
(11)
при условиях
, , , где
.
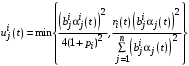Уравнение(11) принимает вид:
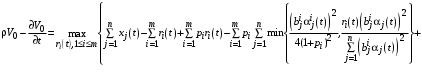
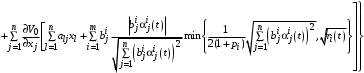. (12)
Функцию Беллмана в нашей ситуации мы считаем линейной:
.
Покажем, что
, , . Приравнивая в (12) коэффициенты при первых степенях 
в левой и правой частях, получаем дифференциальные уравнения для 
:
,
совпадающее с дифференциальными уравнениями (4) с теми же граничными условиями
,
поэтому
, , . (13)
С учетом (13) мы можем переписать (12) в виде:
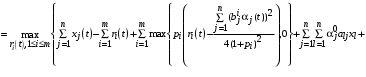
. (14)
Заметим, что безусловная максимизация выражения (14) дает величину ресурсов для агентов влияния, которые все полученные ресурсы тратят на общие цели, равную
.
Но таких агентов нет, так как в этом случае
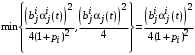
В таком случае Центру невыгодно выделять агенту ресурсы в количестве , так как Центр знает, что агент влияния не все из них
потратит на общие цели.
Так как агент влияния не все ресурсы тратит на общие цели, Центр решает задачу максимизации
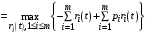. (14)
В таком случае если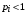
, то Центр выделяет агенту влияния столько ресурсов, сколько тот готов потратить на общие цели, т.е.
(15)
А для остальных агентов (у которых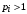
) решается задача линейного программирования
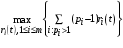
при ограничениях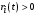
, 
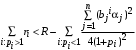
Поэтому, если ,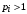 
, то
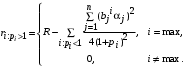
Что говорит о том, что на частные цели есть возможность потратить ресурсы только у агента влияния с максимальным коэффициентом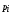
, большим 1.
Остальные агенты, у которых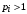 , переходят в разряд тех, которые тратят на ресурсы не все средства, поэтому окончательное решение задачи центра в этом случае
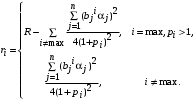
На частные цели агент с номером max тратит количество ресурсов, равное
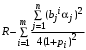
Если же нет агентов, у которых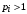
, то у часть ресурсов у центра остаются, причем ни один агент не тратит ресурсы на свои частные цели.
Но безусловная оптимизация возможна при
,
то Центр предоставляет каждому агенту влияния ресурсы в объеме (15). Остается только вопрос, как Центру распределить ресурсы между объектами влияния в случае, если
? Ответ на этот вопрос дает условная максимизация выражения (14).
Пусть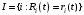
- те агенты, которые все ресурсы тратят только на общие цели. Максимизируя правую часть выражения (14) по
, ,при условии , получаем:
Для агентов, которые все ресурсы тратят на общие цели
.
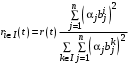где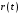
.=
.
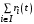Заметив, что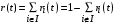
. Тогда
.
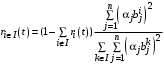Для агентов же, которые не все ресурсы тратят на общие цели, нужно решить следующую задачу:
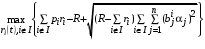
Заметим, что все ресурсы в количестве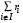
выделяются только одному агенту влияния с максимальным коэффициентом частной деятельности, пусть номер такого агента влияния равен max.
Тогда оптимальное значение величины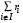 равно
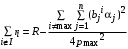, остальные агенты влияния переходят в множество I и вне множества I остается лишь агент с номером max. Всем остальным агентам достаются ресурсы в количестве
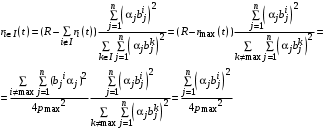
Но тогда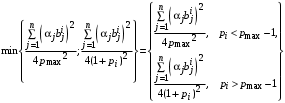
То есть агенты, коэффициент частной деятельности которых незначительно отличается от максимального, получают больше, чем остальные агенты. Но все равно на частные цели они не могут тратить ресурсы.
, получаем .Таким образом, в те моменты времени
, когда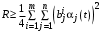 ,оптимальным управлением Центра является
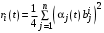, .В те же моменты времени
, когда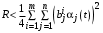 ,оптимальным управлением Центра является
, .Записывая оба выражения для
единой формулой, получаем оптимальное управление Центра: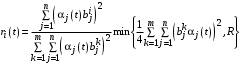 , (36) , ,где
.Зная вид управления (36), мы можем упростить (34), поскольку
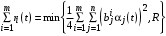,а последнее слагаемое в (34)
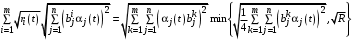
Приравнивая свободные члены в левой и правой частях уравнения (34), получаем дифференциальное уравнение для
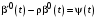: ,где
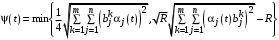, (37)т.е. 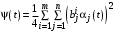, есл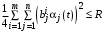и , и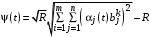 , если 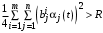.Таким образом, уравнение (37) совпадает с уравнением (17) при тех же самых граничных условиях, следовательно
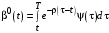.При
имеем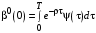 ,где
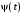
определяется выражением (37).
Таким образом, знаменатель выражения (20)
, т.е. глобальный максимум выигрыша Центра при кооперативном поведении, равен той же самой величине, что и правая часть выражения (19):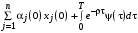 ,где
, определяются формулой (6), а 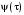, – выражением (18) или (37).Индекс системной согласованности в нашей задаче оказался равным
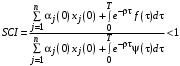,хотя вычисления несколько различались, но ответ получался один и тот же.
Заметим, что системная согласованность возможна только в случае, когда
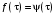, а это возможно только в случае, когда для всех агентов влияния выполняется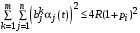 и им просто не хватает ресурсов на общие цели.
6. Случай благожелательного к агенту влияния Центра..
Перейдем теперь к задаче благожелательного к интересам агента влияния Центра:
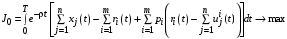, , , , , , , , Выпишем уравнение Гамильтона-Якоби-Беллмана:
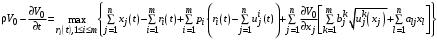
(11)
при условиях
, , , где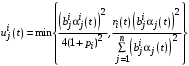 .Уравнение(11) принимает вид:
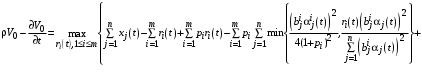
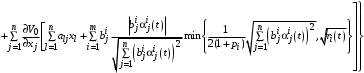. (12)Функцию Беллмана в нашей ситуации мы считаем линейной:
.Покажем, что
, , . Приравнивая в (12) коэффициенты при первых степенях в левой и правой частях, получаем дифференциальные уравнения для : ,совпадающее с дифференциальными уравнениями (4) с теми же граничными условиями
,поэтому
, , . (13)С учетом (13) мы можем переписать (12) в виде:
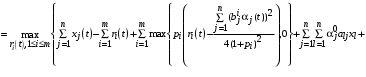
. (14)Заметим, что безусловная максимизация выражения (14) дает величину ресурсов для агентов влияния, которые все полученные ресурсы тратят на общие цели, равную
.Но таких агентов нет, так как в этом случае
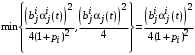
В таком случае Центру невыгодно выделять агенту ресурсы в количестве
, так как Центр знает, что агент влияния не все из них потратит на общие цели.
Так как агент влияния не все ресурсы тратит на общие цели, Центр решает задачу максимизации
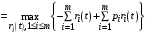. (14)В таком случае если
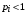, то Центр выделяет агенту влияния столько ресурсов, сколько тот готов потратить на общие цели, т.е. (15)А для остальных агентов (у которых
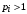) решается задача линейного программирования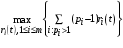 при ограничениях
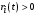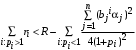
, Поэтому, если
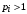, , то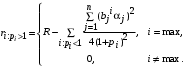 Что говорит о том, что на частные цели есть возможность потратить ресурсы только у агента влияния с максимальным коэффициентом
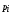, большим 1. Остальные агенты, у которых
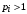, переходят в разряд тех, которые тратят на ресурсы не все средства, поэтому окончательное решение задачи центра в этом случае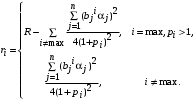 На частные цели агент с номером max тратит количество ресурсов, равное
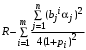
Если же нет агентов, у которых
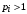
, то у часть ресурсов у центра остаются, причем ни один агент не тратит ресурсы на свои частные цели.
Но безусловная оптимизация возможна при
,то Центр предоставляет каждому агенту влияния ресурсы в объеме (15). Остается только вопрос, как Центру распределить ресурсы между объектами влияния в случае, если
? Ответ на этот вопрос дает условная максимизация выражения (14).Пусть
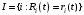- те агенты, которые все ресурсы тратят только на общие цели. Максимизируя правую часть выражения (14) по , ,при условии , получаем:Для агентов, которые все ресурсы тратят на общие цели
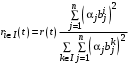.где
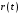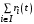.= .Заметив, что
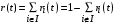. Тогда 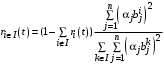.Для агентов же, которые не все ресурсы тратят на общие цели, нужно решить следующую задачу:
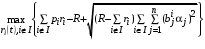
Заметим, что все ресурсы в количестве
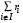выделяются только одному агенту влияния с максимальным коэффициентом частной деятельности, пусть номер такого агента влияния равен max.Тогда оптимальное значение величины
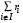равно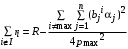 , остальные агенты влияния переходят в множество I и вне множества I остается лишь агент с номером max. Всем остальным агентам достаются ресурсы в количестве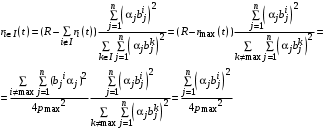 Но тогда
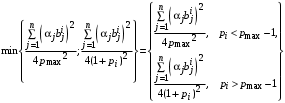
То есть агенты, коэффициент частной деятельности которых незначительно отличается от максимального, получают больше, чем остальные агенты. Но все равно на частные цели они не могут тратить ресурсы.