Файл: Динамическая линейная сочимодель распределения ресурсов в маркетинговых сетях безразличный Центр.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 36
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(9)
Таким образом,
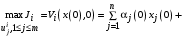
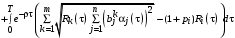 , (10)
, (10)
где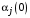 ,
, 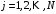 , – компоненты вектора
, – компоненты вектора 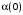 , определяются выражением (6), а
, определяются выражением (6), а 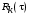 ,
, 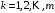 , – выражением (9).
, – выражением (9).
При этом управления определяются выражением (2):
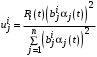 ,
,
где
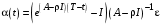 ,
,
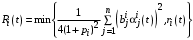 .
.
5. Случай безразличного Центра.
Перейдем теперь к задаче Центра (1)-(2).(5)-(6).
Выпишем уравнение Гамильтона-Якоби-Беллмана:
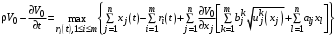
(11)
при условиях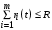 ,
,  ,
,  , где
, где
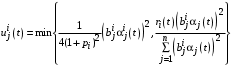 .
.
Уравнение(11) принимает вид:
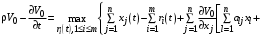
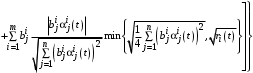 . (12)
. (12)
Функцию Беллмана в нашей ситуации мы считаем линейной:
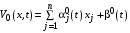 .
.
Покажем, что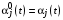 ,
,  ,
,  . Приравнивая в (12) коэффициенты при первых степенях
. Приравнивая в (12) коэффициенты при первых степенях 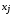 в левой и правой частях, получаем дифференциальные уравнения для
в левой и правой частях, получаем дифференциальные уравнения для 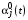 :
:
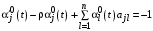 ,
,
совпадающее с дифференциальными уравнениями (4) с теми же граничными условиями
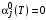 ,
,
поэтому
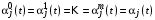 ,
, ,
, 
. (13)
С учетом (13) мы можем переписать (12) в виде:
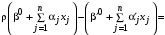
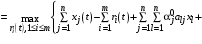
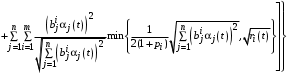 . (14)
. (14)
Заметим, что безусловная максимизация выражения (14) дает величину ресурсов
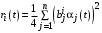 .
.
Но в таком случае
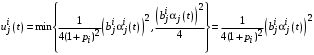
В таком случае Центру невыгодно выделять агенту ресурсы в количестве
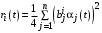 . (15)
. (15)
В таком случае Центр выделяет агенту влияния столько ресурсов, сколько тот готов потратить на общие цели, т.е.
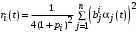
Поэтому, если
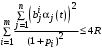 ,
,
то Центр предоставляет каждому агенту влияния ресурсы в объеме (15). Остается только вопрос, как Центру распределить ресурсы между объектами влияния в случае, если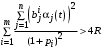 ? Ответ на этот вопрос дает условная максимизация выражения (14).
? Ответ на этот вопрос дает условная максимизация выражения (14).
Максимизируя правую часть выражения (14) по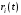 ,
,  ,при условии
,при условии  , получаем
, получаем
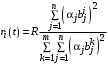 .
.
Таким образом, в те моменты времени , когда
, когда
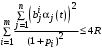 ,
,
оптимальным управлением Центра является
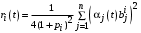 ,
,  .
.
В те же моменты времени , когда
, когда
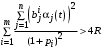 ,
,
оптимальным управлением Центра является
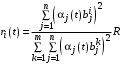 ,
,  .
.
Записывая оба выражения для единой формулой, получаем оптимальное управление Центра:
единой формулой, получаем оптимальное управление Центра:
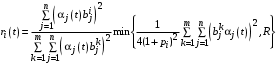 , (16)
, (16)
 ,
,  ,
,
где
 .
.
Зная вид управления (16), мы можем упростить (14), поскольку
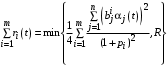 ,
,
а последнее слагаемое в (14)
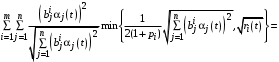
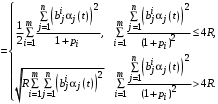 ,
,
Приравнивая свободные члены в левой и правой частях уравнения (14), получаем дифференциальное уравнение для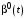 :
:
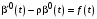 , (17)
, (17)
Решаем уравнение (17) методом вариации произвольной постоянной:
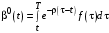 .
.
При имеем
имеем
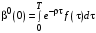 ,
,
Таким образом, максимальный гарантированный выигрыш Центра
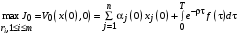 (19)
(19)
где ,
, 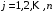 , – компоненты вектора
, – компоненты вектора  , определяются выражением (6), а
, определяются выражением (6), а 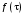 , – выражением (18).
, – выражением (18).
Вычислим индекс системной согласованности
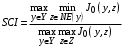 . (20)
. (20)
В нашем случае множество равновесных стратегий каждого агента влияния при заданной стратегии Центра одноточечно, поэтому числитель выражения (20) равен правой части формулы (19).
Чтобы вычислить знаменатель в выражении (20), предположим, что каждый агент влияния максимизирует не свою полезность, а полезность Центра при заданной стратегии Центра, т.е. решает задачу:
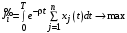 ,
,
(4)-(6).
Выпишем уравнение Гамильтона-Якоби-Беллмана
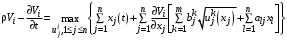 (21)
(21)
при условии .
.
Максимизируя по ,
,  ,
, 
, получаем
 ,
,
и, естественно,
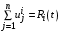 .
.
Поскольку функции Беллмана в нашей ситуации мы считаем линейными,
 , (22)
, (22)
можем записать уравнение (21) с учетом (22) в виде

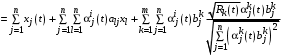 .. (23)
.. (23)
Приравнивая коэффициенты при первых степенях xв левой и правой частях (23), получаем дифференциальные уравнения для коэффициентов :
:
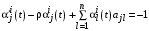 , (24)
, (24)
здесь , совпадающее с уравнением (4), решение которой
, совпадающее с уравнением (4), решение которой
 , (26)
, (26)
в частности, при :
:
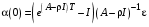 . (27)
. (27)
Выбирая теперь максимальное значение правой части (23) в зависимости от суммы , имеем
, имеем
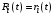 ,
,
что и было изначально понятно, коль скоро агенты влияния заботятся не о своей выгоде, а о выгоде Центра.
Итак, стратегии агентов влияния в данном случае:
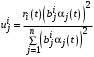 , (28)
, (28)
и, следовательно,
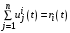 ,
,
где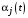 ,
,  – компоненты вектора
– компоненты вектора 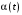 , который определяется выражением (26).
, который определяется выражением (26).
Перейдем к задаче Центра (1)-(2),(5), причем условие (29) с учетом (28) мы можем сразу записать в виде
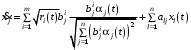 . (30)
. (30)
Выпишем уравнение Гамильтона-Якоби-Беллмана:
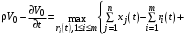
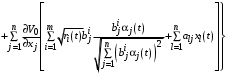 (31)
(31)
при условии ,
,  ,
,  .
.
Функцию Беллмана в нашей ситуации мы считаем линейной:
 ,
,
поэтому уравнение (31) принимает вид:
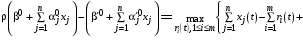
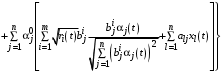 (32)
(32)
при условии ,
,  ,
,  .
.
Покажем, что ,
,  ,
,  . Приравнивая в (32) коэффициенты при первых степенях
. Приравнивая в (32) коэффициенты при первых степенях  в левой и правой частях, получаем дифференциальные уравнения для
в левой и правой частях, получаем дифференциальные уравнения для  :
:
 ,
,
совпадающее с дифференциальными уравнениями (4) с теми же граничными условиями
 ,
,
поэтому
 ,
,  ,
,  . (33)
. (33)
С учетом (33) мы можем переписать (32) в виде:

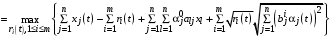 (34)
(34)
при условии ,
,  ,
,  .Заметим, что безусловная максимизация выражения (34) дает величину ресурсов
.Заметим, что безусловная максимизация выражения (34) дает величину ресурсов
 . (35)
. (35)
Таким образом, Центр заинтересован в том, чтобы предоставить каждому агенту влияния i ресурсы в объеме (35). Поэтому, если
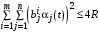 ,
,
то Центр предоставляет каждому агенту влияния ресурсы в объеме (35). Остается только вопрос, как Центру распределить ресурсы между объектами влияния в случае, если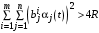 ? Ответ на этот вопрос дает условная максимизация выражения (34).
? Ответ на этот вопрос дает условная максимизация выражения (34).
Максимизируя правую часть выражения (34) по ,
, 
Таким образом,
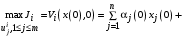
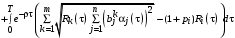 , (10)
, (10)где
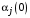 ,
, 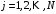 , – компоненты вектора
, – компоненты вектора 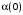 , определяются выражением (6), а
, определяются выражением (6), а 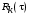 ,
, 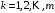 , – выражением (9).
, – выражением (9).При этом управления определяются выражением (2):
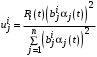 ,
,где
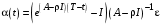 ,
,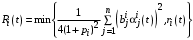 .
.5. Случай безразличного Центра.
Перейдем теперь к задаче Центра (1)-(2).(5)-(6).
Выпишем уравнение Гамильтона-Якоби-Беллмана:
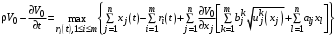
(11)
при условиях
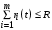 ,
,  ,
,  , где
, где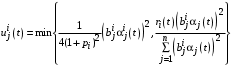 .
.Уравнение(11) принимает вид:
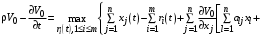
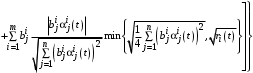 . (12)
. (12)Функцию Беллмана в нашей ситуации мы считаем линейной:
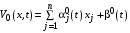 .
.Покажем, что
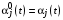 ,
,  ,
,  . Приравнивая в (12) коэффициенты при первых степенях
. Приравнивая в (12) коэффициенты при первых степенях 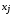 в левой и правой частях, получаем дифференциальные уравнения для
в левой и правой частях, получаем дифференциальные уравнения для 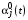 :
: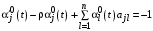 ,
,совпадающее с дифференциальными уравнениями (4) с теми же граничными условиями
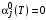 ,
,поэтому
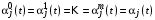 ,
, ,
, 
. (13)
С учетом (13) мы можем переписать (12) в виде:
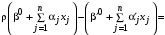
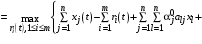
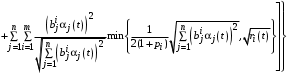 . (14)
. (14)Заметим, что безусловная максимизация выражения (14) дает величину ресурсов
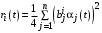 .
.Но в таком случае
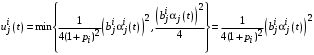
В таком случае Центру невыгодно выделять агенту ресурсы в количестве
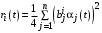 . (15)
. (15)В таком случае Центр выделяет агенту влияния столько ресурсов, сколько тот готов потратить на общие цели, т.е.
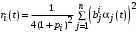
Поэтому, если
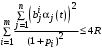 ,
,то Центр предоставляет каждому агенту влияния ресурсы в объеме (15). Остается только вопрос, как Центру распределить ресурсы между объектами влияния в случае, если
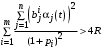 ? Ответ на этот вопрос дает условная максимизация выражения (14).
? Ответ на этот вопрос дает условная максимизация выражения (14).Максимизируя правую часть выражения (14) по
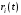 ,
,  ,при условии
,при условии  , получаем
, получаем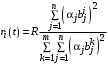 .
.Таким образом, в те моменты времени
 , когда
, когда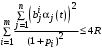 ,
,оптимальным управлением Центра является
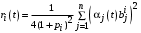 ,
,  .
.В те же моменты времени
 , когда
, когда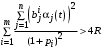 ,
,оптимальным управлением Центра является
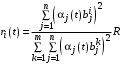 ,
,  .
.Записывая оба выражения для
 единой формулой, получаем оптимальное управление Центра:
единой формулой, получаем оптимальное управление Центра:
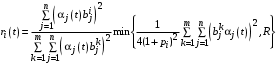 , (16)
, (16) ,
,  ,
,где
 .
.Зная вид управления (16), мы можем упростить (14), поскольку
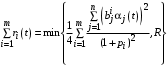 ,
,а последнее слагаемое в (14)
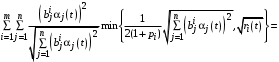
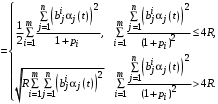 ,
,Приравнивая свободные члены в левой и правой частях уравнения (14), получаем дифференциальное уравнение для
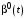 :
: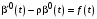 , (17)
, (17)Решаем уравнение (17) методом вариации произвольной постоянной:
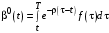 .
.При
 имеем
имеем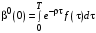 ,
,Таким образом, максимальный гарантированный выигрыш Центра
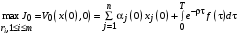 (19)
(19)где
 ,
, 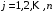 , – компоненты вектора
, – компоненты вектора  , определяются выражением (6), а
, определяются выражением (6), а 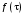 , – выражением (18).
, – выражением (18).Вычислим индекс системной согласованности
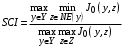 . (20)
. (20)В нашем случае множество равновесных стратегий каждого агента влияния при заданной стратегии Центра одноточечно, поэтому числитель выражения (20) равен правой части формулы (19).
Чтобы вычислить знаменатель в выражении (20), предположим, что каждый агент влияния максимизирует не свою полезность, а полезность Центра при заданной стратегии Центра, т.е. решает задачу:
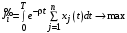 ,
,(4)-(6).
Выпишем уравнение Гамильтона-Якоби-Беллмана
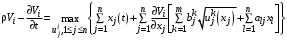 (21)
(21)при условии
 .
. Максимизируя по
 ,
,  ,
, 
, получаем
 ,
, и, естественно,
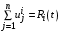 .
. Поскольку функции Беллмана в нашей ситуации мы считаем линейными,
 , (22)
, (22)можем записать уравнение (21) с учетом (22) в виде

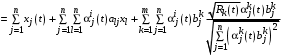 .. (23)
.. (23)Приравнивая коэффициенты при первых степенях xв левой и правой частях (23), получаем дифференциальные уравнения для коэффициентов
 :
: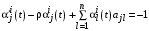 , (24)
, (24)здесь
 , совпадающее с уравнением (4), решение которой
, совпадающее с уравнением (4), решение которой , (26)
, (26)в частности, при
 :
: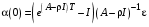 . (27)
. (27)Выбирая теперь максимальное значение правой части (23) в зависимости от суммы
 , имеем
, имеем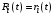 ,
,что и было изначально понятно, коль скоро агенты влияния заботятся не о своей выгоде, а о выгоде Центра.
Итак, стратегии агентов влияния в данном случае:
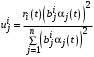 , (28)
, (28)и, следовательно,
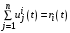 ,
,где
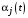 ,
,  – компоненты вектора
– компоненты вектора 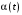 , который определяется выражением (26).
, который определяется выражением (26).Перейдем к задаче Центра (1)-(2),(5), причем условие (29) с учетом (28) мы можем сразу записать в виде
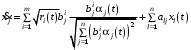 . (30)
. (30) Выпишем уравнение Гамильтона-Якоби-Беллмана:
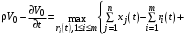
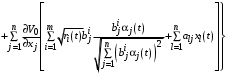 (31)
(31)при условии
 ,
,  ,
,  .
.Функцию Беллмана в нашей ситуации мы считаем линейной:
 ,
,поэтому уравнение (31) принимает вид:
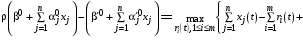
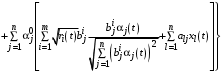 (32)
(32)при условии
 ,
,  ,
,  .
.Покажем, что
 ,
,  ,
,  . Приравнивая в (32) коэффициенты при первых степенях
. Приравнивая в (32) коэффициенты при первых степенях  в левой и правой частях, получаем дифференциальные уравнения для
в левой и правой частях, получаем дифференциальные уравнения для  :
: ,
,совпадающее с дифференциальными уравнениями (4) с теми же граничными условиями
 ,
,поэтому
 ,
,  ,
,  . (33)
. (33)С учетом (33) мы можем переписать (32) в виде:

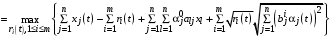 (34)
(34)при условии
 ,
,  ,
,  .Заметим, что безусловная максимизация выражения (34) дает величину ресурсов
.Заметим, что безусловная максимизация выражения (34) дает величину ресурсов . (35)
. (35)Таким образом, Центр заинтересован в том, чтобы предоставить каждому агенту влияния i ресурсы в объеме (35). Поэтому, если
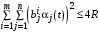 ,
,то Центр предоставляет каждому агенту влияния ресурсы в объеме (35). Остается только вопрос, как Центру распределить ресурсы между объектами влияния в случае, если
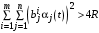 ? Ответ на этот вопрос дает условная максимизация выражения (34).
? Ответ на этот вопрос дает условная максимизация выражения (34).Максимизируя правую часть выражения (34) по
 ,
, 