С учетом этого



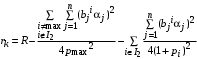
где

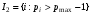
На частные цели может потратить средства лишь агент влияния с номером max в количестве 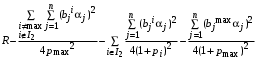. Но это возможно только в случае, если 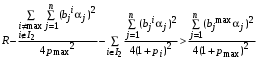. В противном случае агент с максимальной мощностью частной деятельности получает от центра меньше ресурсов, чем он бы получил в случае, если бы он входил во множество I, и, следовательно, на частные цели ему в таком случае ресурсов не остается, а, следовательно, множество I пусто.

В случае, если даже агент с максимальной мощностью частной деятельности не может потратит на общие цели ресурсы, то 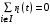и все агенты тратят ресурсы только на общие цели и


Таким образом, в те моменты времени , когда

,

оптимальным управлением Центра является



, .

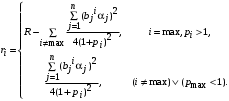
В те же моменты времени , когда

,

оптимальным управлением Центра является

, .

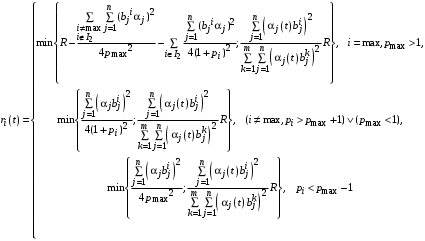Записывая оба выражения для единой формулой не будем в силу громоздкости

Рассуждая как в предыдущем пункте, получим:

1)В случае



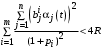
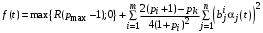
2)В случае

2a) если

---

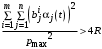
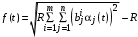
2b) если

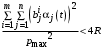
Снова 2 случая:

Случай 1.



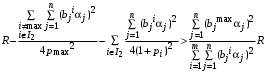
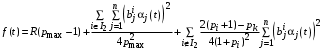
Случай 2.



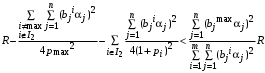
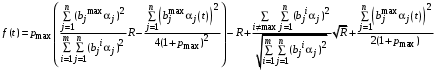
Приравнивая свободные члены в левой и правой частях уравнения (14), получаем дифференциальное уравнение для :

. (17)

Решаем уравнение (17) методом вариации произвольной постоянной:

.

При имеем

,

Таким образом, максимальный гарантированный выигрыш Центра

(19)

где , , – компоненты вектора , определяются выражением (6), а , – выражением (18).

Вычислим индекс системной согласованности

. (20)

Чтобы вычислить знаменатель в выражении (20), предположим, что каждый агент влияния максимизирует не свою полезность, а полезность Центра при заданной стратегии Центра, т.е. решает задачу:

,



, , ,

, .

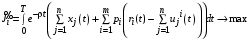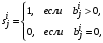
Выпишем уравнение Гамильтона-Якоби-Беллмана:

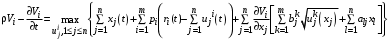(21)

при условии .

Максимизируя по , ,

---

, получаем

,

и, естественно,

.

Поскольку функции Беллмана в нашей ситуации мы считаем линейными,

, (22)

можем записать уравнение (21) с учетом (22) в виде



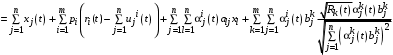. (23)

Приравнивая коэффициенты при первых степенях xв левой и правой частях (23), получаем дифференциальные уравнения для коэффициентов :

, (24)

здесь , совпадающее с уравнением (4). Тогда

, (26)

в частности, при :

. (27)

Выбирая теперь максимальное значение правой части (23) в зависимости от суммы , имеем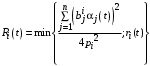

.

Итак, стратегии агентов влияния в данном случае:

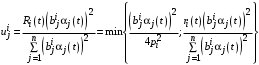, (28)

где , – компоненты вектора , который определяется выражением (26).

Перейдем к задаче Центра.

,

, , , ,

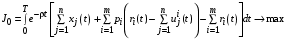, , , (29)

причем условие (29) с учетом (28) мы можем сразу записать в виде

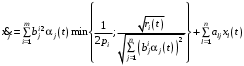. (30)

Выпишем уравнение Гамильтона-Якоби-Беллмана. Пусть

---

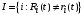
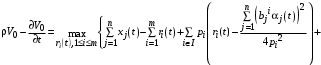
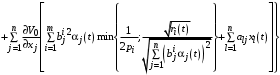(31)

при условии , , .

Функцию Беллмана в нашей ситуации мы считаем линейной:

,

поэтому уравнение (31) принимает вид:



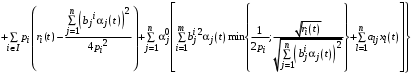(32)

при условии , , .

Покажем, что , , . Приравнивая в (32) коэффициенты при первых степенях в левой и правой частях, получаем дифференциальные уравнения для :

,

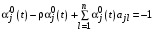совпадающее с дифференциальными уравнениями (4) с теми же граничными условиями

,

поэтому

, , . (33)

С учетом (33) мы можем переписать (32) в виде:



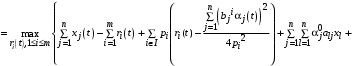
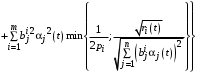(34)

при условии , , .

Заметим, что безусловная максимизация выражения (34) дает величину ресурсов

. (35)

для агентов, которые тратят все ресурсы на общие цели. Среди таковых не может быть агентов с

---

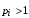чего быть не может, так как оптимальная величина ресурсов, которые агент влияния тратит на общие цели 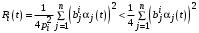и, следовательно, такие агенты не потратят все ресурсы на общие цели.

Для остальных же агентов (у которых 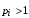), по аналогии с решением предыдущей задачи, решая задачу линейного программирования, получим, что всем оставшимся агентам нужно выделить ровно то количество ресурсов, которое они готовы потратить на общие цели за исключением агента,у которого максимальная мощность частной деятельности (пусть номер этого агента - max).

Т.е.

.

.

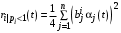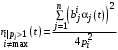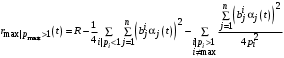. (35)
Таким образом, Центр заинтересован в том, чтобы предоставить каждому агенту влияния i ресурсы в объеме (35). Поэтому, если

,

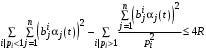то Центр предоставляет каждому агенту влияния ресурсы в объеме (35). Остается только вопрос, как Центру распределить ресурсы между объектами влияния в случае, если 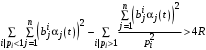? Ответ на этот вопрос дает условная максимизация выражения (34).

Максимизируя правую часть выражения (34) по , ,при условии , получаем для агентов, которые тратят все ресурсы на общие цели

.

обозначив сумму через .
Заметив, что . Тогда

.

Для агентов же, которые не все ресурсы тратят на общие цели, нужно решить следующую задачу:



Заметим, что все ресурсы в количестве выделяются только одному агенту влияния с максимальным коэффициентом частной деятельности, пусть номер такого агента влияния равен max.

---

Смотрите также файлы

• Автореферат бакалаврской работы.docx

• Экономика организации.3.docx

• Проверяемое задание 4 Глава Методы коррекционной работы. Составление программы психокоррекционной работы.docx

• Практические задания 1 3.docx

• Занятие здорово здоровым быть.docx