Тогда оптимальное значение величины равно

, остальные агенты влияния переходят в множество I и вне множества I остается лишь агент с номером max. Всем остальным агентам достаются ресурсы в количестве



Но тогда

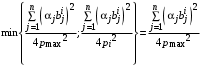
С учетом этого



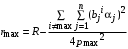
На частные цели может потратить средства лишь агент влияния с номером max в количестве 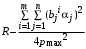. Но это возможно только в случае, если 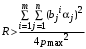. В противном случае агент с максимальной мощностью частной деятельности получает от центра меньше ресурсов, чем он бы получил в случае, если бы он входил во множество I, и, следовательно, на частные цели ему в таком случае ресурсов не остается, а, следовательно, множество I пусто.

В случае, если даже агент с максимальной мощностью частной деятельности не может потратит на общие цели ресурсы, то и все агенты тратят ресурсы только на общие цели и


Таким образом, в те моменты времени , когда

,

оптимальным управлением Центра является



, .

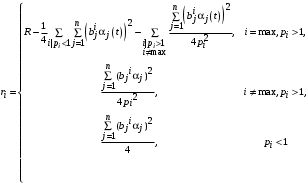
В те же моменты времени , когда

,

оптимальным управлением Центра является

, .

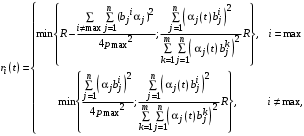Записывая оба выражения для единой формулой не будем в силу громоздкости

Рассуждая как в предыдущем пункте, получим:

1)В случае



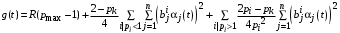
2)В случае

---

2a) если и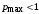



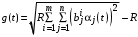
2b) если и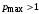



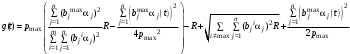
2c) если


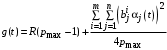
Таким образом, уравнение (37) совпадает с уравнением (17) при тех же самых граничных условиях, следовательно

.

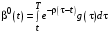При имеем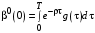

,

где 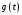определяется выражением (37).

Таким образом, знаменатель выражения (20) , т.е. глобальный максимум выигрыша Центра при кооперативном поведении, равен той же самой величине, что и правая часть выражения (19):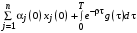

,

где , определяются формулой (6), а , – выражением (18) или (37).

Индекс системной согласованности в нашей задаче оказался равным

,
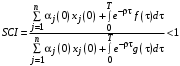Заключение.

В случае линейных функций частного дохода базовых агентов найдены единственные равновесия по Нэшу и Парето-оптимальное решение. Доказано, что ценность агента влияния для всех базовых агентов одинакова и зависит только от его связей. Доказано, что базовый агент тратит на повышение заинтересованности агента влияния меньше средств, чем считает нужным Центр. Также благожелательный Центр считает, что агент влияния должен потратить на общие интересы меньше ресурсов, чем Центр, безразличный к частным интересам агента.

Полученные результаты планируется распространить на случай степенной вогнутой функции частного дохода, а также на случай произвольной производственной функции.

---

---

Смотрите также файлы

• Автореферат бакалаврской работы.docx

• Экономика организации.3.docx

• Проверяемое задание 4 Глава Методы коррекционной работы. Составление программы психокоррекционной работы.docx

• Практические задания 1 3.docx

• Занятие здорово здоровым быть.docx