Файл: Методические указания к выполнению контрольной работы 3 для студентов зф и идо.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 06.11.2023

Просмотров: 197

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Список литературы

Содержание контрольной работы № 3

Длина волны де Бройля, следовательно, равна

ЭЛЕКТРОПРОВОДНОСТЬ ТВЕРДЫХ ТЕЛ1. В изолированных атомах электроны находятся в дискретных энергетических состояниях. У одиночных атомов одного элемента, расположенных на таких больших расстояниях , что взаимодействием между ними можно пренебречь ( , где – постоянная кристаллической решетки), энергия соответствующих энергетических уровней абсолютно одинакова. Так как потенциальная энергия взаимодействия электрона с ядром атома обратно пропорциональна расстоянию между ними ,то атом является для электрона потенциальной ямой, внутри которой электроны находятся на определенных энергетических уровнях. При этом между соседними атомами имеется высокий и широкий потенциальный барьер.При сближении атомов взаимодействие между ними растет. При этом для всех электронов в атомах уменьшается как ширина ( ), так и высота потенциального барьера, причем для валентных электронов высота потенциального барьера может стать ниже их энергетического уровня в изолированном атоме. В этом случае валентные электроны получают возможность легко переходить от одного атома к другому. Такие обобществленные кристаллом электроны называют свободными, а их совокупность – электронным газом.Взаимодействие атомов в кристалле существенно меняет структуру энергетических уровней электронов. При сближении атомов каждый энергетический уровень изолированного атома расщепляется на очень близко расположенных уровней, образующих зону разрешенных энергий. Разрешенные зоны отделены друг от друга запрещенными зонами.Расщепление разных уровней не одинаково. Наибольшее расщепление испытывают высоко расположенные уровни как занятые, так и не занятые электронами. Поэтому зона, соответствующая валентным электронам, оказывается широкой. Для электронов, расположенных на нижних энергетических уровнях атома, потенциальный барьер, после сближения, остается очень трудно проходимым, поэтому соответствующие энергетические уровни практически не расщепляются (рис. 5.1). Следует отметить, что ширина зон не зависит от размеров кристалла. Поэтому, чем больше атомов содержит кристалл, тем теснее располагаются уровни внутри разрешенной зоны. Для кристалла, состоящего, например, из 1023 атомов, расстояние между соседними уровнями зоны составляет примерно 10-23 эВ. Рис. 5.1. Схема образования энергетических зон при сближении атомов(а – постоянная решетки кристалла)2. Существование энергетических зон позволяет объяснить с единой точки зрения различие электрофизических характеристик металлов, полупроводников и диэлектриков.Электрические свойства твердых тел зависят от характера заполнения электронами разрешенных и от ширины запрещенных энергетических зон. Заполнение электронами энергетических уровней в разрешенной зоне осуществляется в соответствии с принципом Паули, согласно которому в системе не может быть даже двух электронов с одинаковым набором всех квантовых чисел. В атоме этими числами являются: – главное квантовое число, – орбитальное, – магнитное, – магнитное спиновое квантовое число.Возможны три случая (рис 5.2). В случае (а) электроны заполняют валентную зону не полностью. Поэтому достаточно сообщить электронам, находящимся на верхних уровнях, совсем небольшую энергию (


Министерство образования и науки Российской Федерации
Новосибирский государственный технический университет

___________________________________________________________

ФИЗИКА
Методические указания

к выполнению контрольной работы № 3

для студентов ЗФ и ИДО

направлений "Эксплуатация транспортно-технологических машин и комплексов" и "Конструкторско-технологическое обеспечение машиностроительных производств" (специальный курс)


Новосибирск

2014


Составители: Л.М. Родникова, Н.Я. Усольцева, В.В. Христофоров

Рецензенты: А.В. Баранов, Н.Ю. Березин

Работа подготовлена на кафедре общей физики

 Новосибирский государственный

технический университет, 2014 г.
Вопросы, которые выносятся на экзамен


  1. Опытное обоснование корпускулярно-волнового дуализма вещества. Гипотеза де Бройля, волны де Бройля.

  2. Соотношение неопределенностей Гейзенберга как проявление корпускулярно-волнового дуализма вещества.

  3. Волновая функция, ее физический смысл. Уравнение Шредингера для стационарных состояний.

  4. Решение уравнения Шредингера для частицы в одномерной бесконечно глубокой прямоугольной потенциальной яме.

  5. Туннельный эффект.

  6. Квантовый гармонический осциллятор.

  7. Применение уравнения Шредингера для описания атома водорода.

  8. Главное, орбитальное и магнитное квантовые числа, их физический смысл. Спин электрона. Принцип Паули. Распределение электронов в атоме по состояниям.

  9. Расщепление энергетических уровней атомов при образовании молекул.

  10. Тепловые колебания кристаллической решетки. Теплоемкость кристаллической решетки. Фононы.

  11. Функция распределения Ферми-Дирака. Ее физический смысл. Вырождение электронного газа.

  12. Понятие о квантовой статистике Бозе-Эйнштейна.

  13. Влияние температуры на распределение электронов проводимости в металле по энергиям. Теплоемкость электронного газа.

  14. Электропроводность металлов. Зависимость от температуры.

  15. Элементы зонной теории. Расщепление энергетических уровней атомов и образование энергетических зон в кристаллах.

  16. Металлы, диэлектрики и полупроводники с точки зрения зонной теории твердого тела.

  17. Собственные полупроводники. Электропроводность и ее зависимость от температуры.

  18. Примесные полупроводники. Электропроводность и ее зависимость от температуры.

  19. Фотопроводимость полупроводников.

  20. Контакт электронного и дырочного полупроводника (p-n переход), его вольт-амперная характеристика. Физические процессы в p-n переходе.

  21. Принцип работы транзистора.

  22. Состав ядра. Дефект массы и энергия связи ядра. Взаимодействие нуклонов, ядерные силы. Устойчивость ядер.

  23. Естественная радиоактивность. Закон радиоактивного распада.

  24. Ядерные реакции и законы сохранения. Применение ядерной энергии в народном хозяйстве.

  25. Реакции деления и синтеза атомных ядер.

  26. Элементарные частицы, их классификация и взаимная превращаемость.


Примечание. Выделены основные вопросы.

Список литературы





  1. Савельев И.В. Курс общей физики. – М.: Наука, 1989 – Т.3; 1998. – Кн. 5, и последующие издания этого курса.

  2. Трофимова Т.И. Курс физики. – М.: Высшая школа, 1985, 1990, 1994, 1997 – 1999, и последующие издания этого курса.

  3. Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, 1989, 1999, и последующие издания этого курса.

  4. Епифанов Г.И. Физика твердого тела. – М.: Высшая школа, 1977, и последующие издания этого курса

  5. Бушманов Б.Н., Хромов Ю.А. Физика твердого тела. – М.: Высшая школа, 1971, и последующие издания этого курса.

  6. Чертов А.Г., Воробьев А.А. Задачник по физике. – М.: Высшая школа, 1981, 1988, и последующие издания этого курса.



Контрольная работа № 3

Содержание контрольной работы № 3





Темы
Номера задач

1. Длина волны де Бройля
301 – 310

2. Соотношение неопределенностей Гейзенберга
311 – 320

3. Уравнение Шредингера
321 – 330

4. Теплоемкость твердых тел
331 – 340

5. Квантовая статистика Ферми-Дирака
341 – 350

6. Электропроводность твердых тел
351 – 360

7. Ядерные реакции. Радиоактивность
361 – 370


Рассмотрим элементы теории по каждой из указанных тем и примеры решения задач.


Тема 1. ДЛИНА ВОЛНЫ ДЕ БРОЙЛЯ
Изучение природы света показало, что наряду с волновыми он обладает корпускулярными свойствами. Таким образом, в оптических явлениях проявляется корпускулярно-волновой дуализм (двойственность) света. В 1924 г. Луи де Бройль выдвинул гипотезу, что дуализм не является особенностью только оптических явлений, а имеет универсальное проявление. Движение любой частицы согласно де Бройлю должно описываться волновым процессом, длина волны которого

, (1.1)

где – импульс частицы, – постоянная Планка.

Гипотеза де Бройля была вскоре подтверждена экспериментально (опыты Дэвиссона и Джермера (1927)). Волновыми свойствами обладают все тела, но проявляются они только для частиц с малой массой (микрочастиц), так как для них длина волны де Бройля достаточно велика. Причем, микрочастица должна находиться в условиях, когда её длина волны де Бройля будет соизмерима с размерами той области пространства, в которой частица движется. Например, при движении электрона внутри телевизионной трубки, линейные размеры которой намного больше длины волны де Бройля электрона, учитывать волновые свойства электрона не имеет смысла. При движении же электрона внутри кристалла, расстояние между атомами которого по порядку величины равно его длине волны де Бройля, учитывать волновые свойства электрона необходимо.

Задача. Найти длину волны де Бройля для электрона, имеющего кинетическую энергию: а) W1 = 10 кэВ; б) W2 = 1 МэВ.
Дано: W1 = 10 кэВ =104 эВ = 104 Дж

W2 = 1 МэВ =106 эВ = 106 Дж



1  ?, 2  ?
Решение. Длина волны де Бройля определяется по формуле (1.1). Импульс частицы р для скоростей, малых по сравнению со скоростью света в вакууме (v  c),

p = mv .

Учитывая, что импульс можно выразить через кинетическую энергию , для длины волны де Бройля получаем

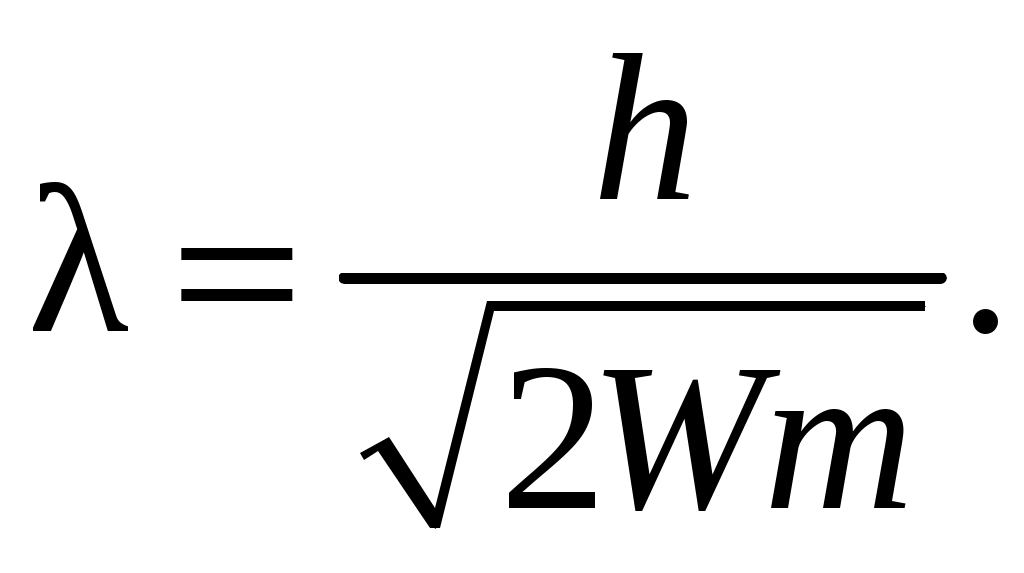(1.2)

Если же скорость частицы нельзя считать малой по сравнению со скоростью света в вакууме, то импульс частицы согласно релятивистской теории,

,

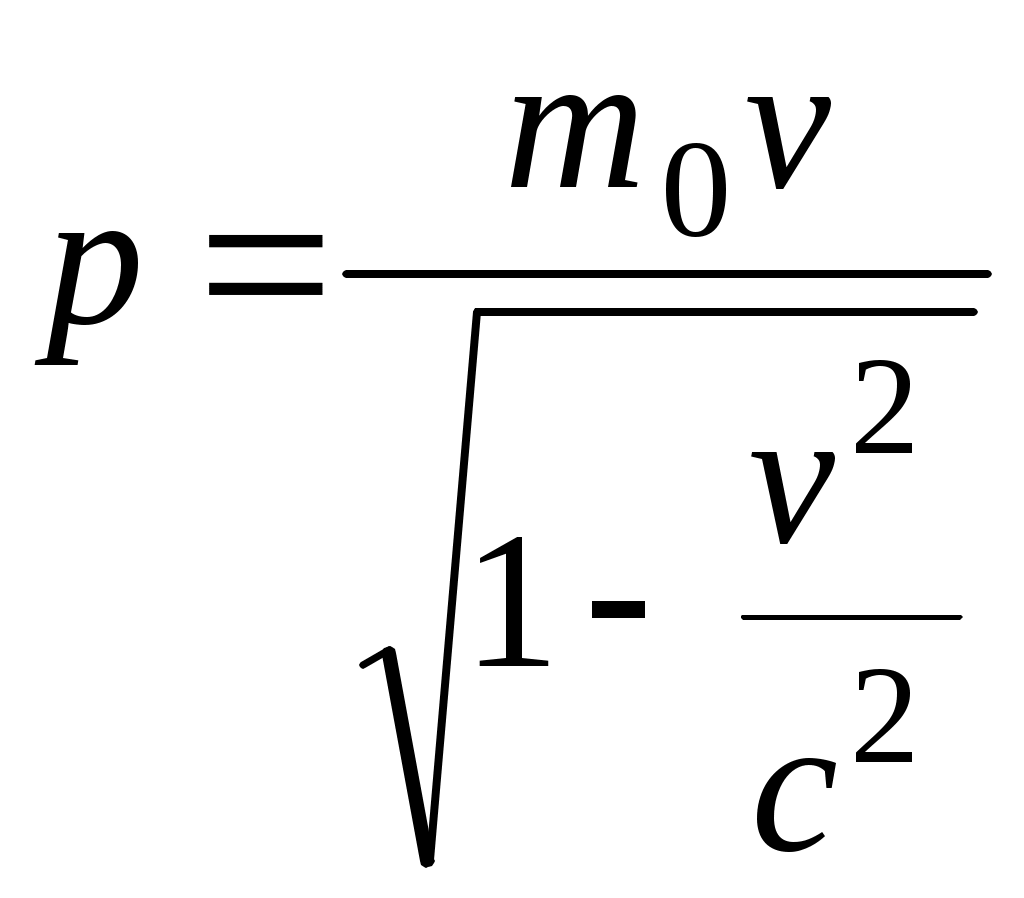
где – масса покоя частицы.

Выражение импульса через кинетическую энергию в этом случае имеет вид

.

Длина волны де Бройля, следовательно, равна


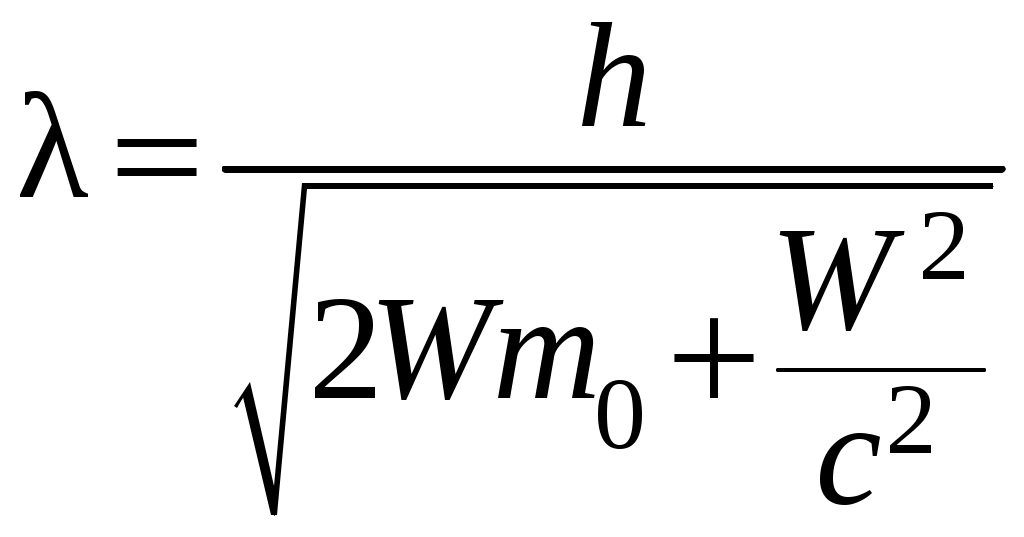. (1.3)

Видно, что формула (1.3) переходит в формулу (1.2), если членом по сравнению с членом можно пренебречь.

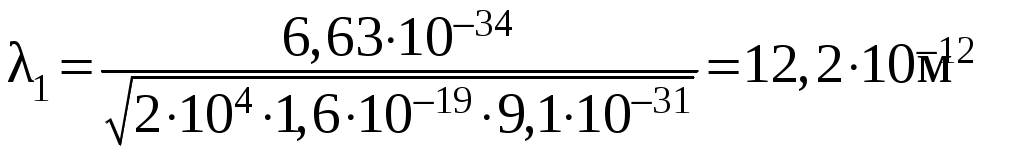Оценка показывает, что в случае а) член составляет менее 1 от члена . Следовательно, пользуемся формулой (1.2), из которой получаем

.

Для случая б) пользуемся формулой (1.3),из которой получаем
.

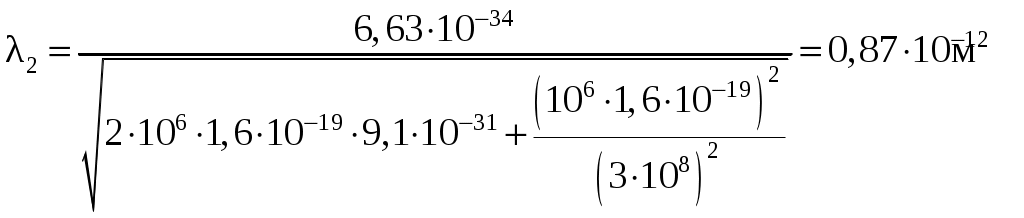Ответ: а) ; б) .

Тема 2. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ГЕЙЗЕНБЕРГА
В
Рис. 2.1.

Монохроматическая волна и

волновой пакет
классической механике точность определения координаты и импульса материальной точки в один и тот же момент времени в принципе не ограничена. Волновые же свойства микрочастиц ограничивают эту точность. Дадим качественное объяснение этого утверждения. Определенная длина волны есть характеристика идеализированной бесконечной по протяженности монохроматической волны, описываемой синусоидой (рис. 2.1,а). Любая же реальная волна, в том числе волна де Бройля, занимает конечную область пространства, как говорят, является волновым пакетом (рис 2.1,б). Математически волновой пакет может быть представлен как результат суперпозиции синусоид с различны дли-

н


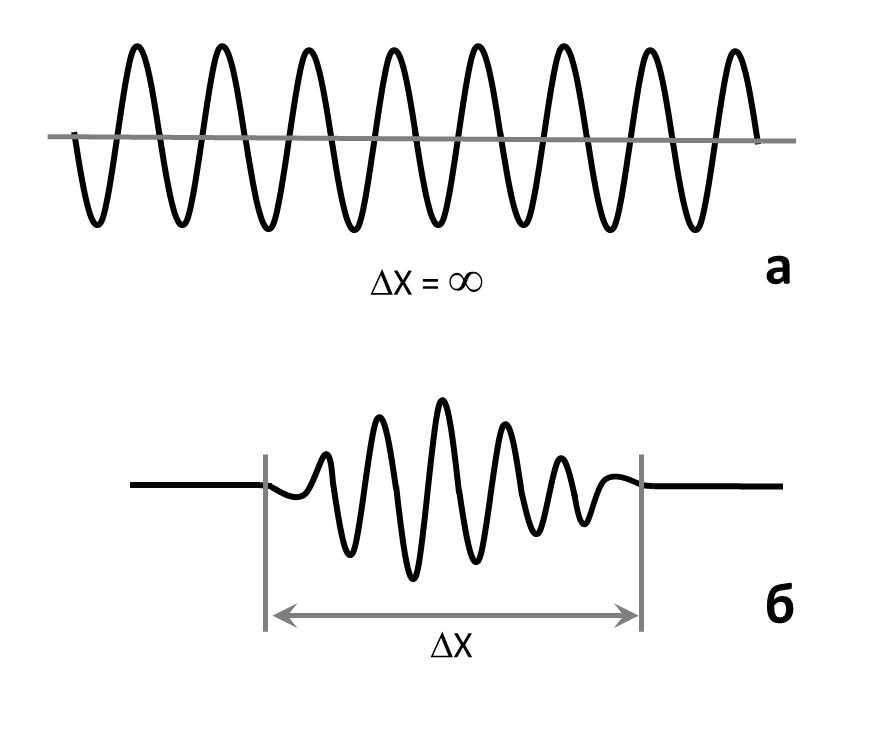
Рис. 2.1. Монохроматическая волна и волновой пакет
ами волн, численные значения которых лежат в определенном диапазоне . Поскольку длина волны де Бройля и импульс частицы связаны соотношением (1.1), то ясно, что если длины волн лежат в некотором диапазоне

Смотрите также файлы