Файл: Методические указания к выполнению контрольной работы 3 для студентов зф и идо.doc

, то в некотором диапазоне p лежат и значения импульса. Величина , а следовательно, p растет при уменьшении размеров волнового пакета . Размер волнового пакета характеризует неопределенность координаты микрочастицы. Из сказанного следует, что уменьшение величины приводит к увеличению неопределенности импульса p. Гейзенберг показал, что сделанное утверждение можно выразить с помощью системы неравенств, которые называются соотношениями неопределенности:

; (2.1)

; (2.2)

, (2.3)

где - неопределенность координат частицы; – неопределенность проекций импульса на указанные оси координат; – постоянная Планка с чертой.

Соотношением неопределенности связаны также время пребывания частицы в некотором энергетическом состоянии с неопределенностью энергии этого состояния :

. (2.4)
Применительно к электрону в атоме это означает следующее. В стационарном состоянии атом может находиться как угодно долго . Именно поэтому энергия данного состояния имеет вполне определенное значение . «Время жизни» возбужденного состояния атома имеет конечную величину порядка t = 10^8c. Следовательно, неопределенность энергии этого состояния конечна:

---

. Если при переходе электрона из возбужденного состояния в стационарное атом испускает квант света (фотон), то энергия указанного фотона будет иметь такую же неопределенность .

Задача. При переходе из возбужденного состояния в стационарное атом за время  = 10^8 секунды испустил фотон, длина волны которого  = 0,55 мкм. Оцените величину неопределенности, с которой можно установить координату фотона в направлении его движения, а также относительную неопределенность его длины волны.

Дано:  = 0,55 мкм =0,5510^6м.

 = t = 10^8с.



x –      

Решение. Неопределенность координаты можно оценить так:

x  ct,

где с  скорость света. Численно это дает x  310⁸10^8 = 3 м.

Для определения относительной неопределенности длины волны воспользуемся соотношением неопределенности Гейзенберга для энергии возбужденного состояния и времени пребывания в этом состоянии

. (2.5)

Знак равенства в формуле (2.5) означает, что ищется минимально возможная неопределенность энергии . Выше отмечалось, что такую же неопределенность будет иметь и испущенный атомом фотон. Поскольку энергия фотона связана с частотой световой волны формулой E_ф = h, то неопределенности энергии фотона соответствует неопределенность частоты, равная
  E  h . (2.6)
Частоту можно выразить через длину волны в вакууме   с  . Используя её можно найти связь между дифференциалами частоты и длины волны:

.

Опуская знак минус, который означает, что увеличению частоты соответствует уменьшение длины волны, и заменив знак дифференциала знаком неопределенности, получим

.

Подставляя последнее выражение в (2.6), а также используя соотношение (2.5), имеем

---

.
Учитывая, что , для относительной неопределенности длины волны фотона из последней формулы получаем
.
Подставляя в это выражение численные значения, получим

.
Ответ:3 м, 310^-8.

Тема 3. УРАВНЕНИЕ ШРЕДИНГЕРА
Второй закон Ньютона, являясь основным уравнением классической динамики, позволяет, зная начальные условия, рассчитывать положение и скорость частицы в любой момент времени. В микромире любая частица описывается волной де Бройля. Следовательно, необходимо иметь уравнение, с помощью которого можно рассчитывать параметры такой частицы-волны для любой точки пространства в любой момент времени. Такое уравнение было предложено Шредингером (1926):
,

где m – масса частицы; U(x,y,z,t) – потенциальная энергия; – мнимая единица; t – время; x,y,z – координаты. Это уравнение является основным законом квантовой нерелятивистской механики.

Искомой величиной при решении данного уравнения является волновая  – функция (пси – функция), которая в общем случае зависит от координат и времени x, y, z, t). У самой  – функции нет физического смысла. Физический смысл имеет квадрат модуля –функции , который равен плотности вероятности обнаружить частицу-волну в данной точке пространства в данный момент времени:

,

где – вероятность обнаружить частицу в пределах бесконечно малого объема . Чтобы квадрат модуля –функции соответствовал своему физическому смыслу, сама –функция должна быть конечна, однозначна и непрерывна, а ее производные – конечны и однозначны. Кроме того, поскольку вероятность события, которое обязательно произойдет, в математике считается равной единице, то этому так называемому условию нормировки должна удовлетворять и  – функция.

---

Если потенциальная энергия частицы не зависит от времени, то  – функцию можно заменить произведением двух функций, одна из которых зависит только от координат, а другая – только от времени:
x, y, z, t) = x, y, z t.
Такая замена позволяет разбить уравнение Шредингера на два. Одно из них зависит только от координат, оно называется стационарным уравнением Шредингера, а второе – от времени. При этом решение второго уравнения, оказывается, не влияет на искомую плотность вероятности:

.

Стационарное уравнение Шредингера для одномерного движения частицы вдоль оси имеет вид

,
где Е – полная энергия частицы-волны.

Рассмотрим с квантово-механической точки зрения задачу о поведении частицы, находящейся в ограниченной области пространства. Будем считать, что частица может перемещаться только вдоль оси координат , причем, для выхода за пределы области необходимо сообщить частице бесконечно большую энергию. Иначе говоря, решим уравнение Шредингера для частицы, находящейся в одномерной, бесконечно глубокой потенциальной яме. Будем считать потенциальную энергию частицы внутри ямы равной нулю (рис. 3.1):

U = 0 при 0  x  l;

U =  при x  0, x  l.

Тогда уравнение Шредингера для области 0  x  l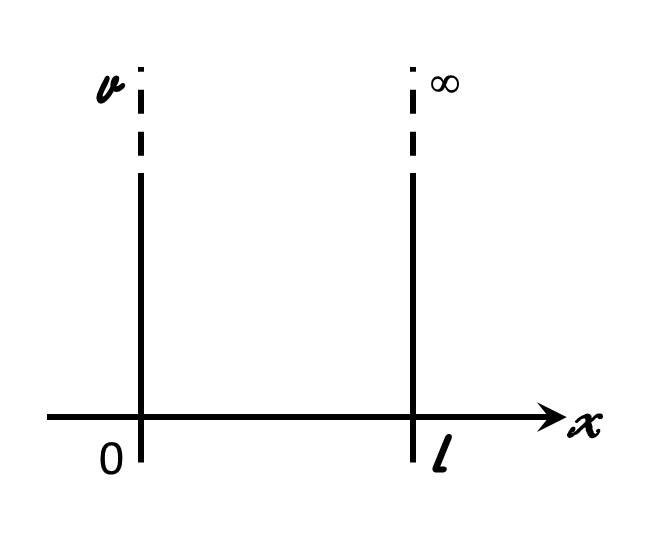


Рис. 3.1 Зависимость потенци-альной энергии от координаты
, или .

Введем обозначение

. (3.1)

Тогда уравнение принимает вид

.

Решением этого уравнения является функция

---

,

где .
Поскольку частица не может выйти за пределы бесконечно глубокой потенциальной ямы, или иначе, стенки ямы абсолютно непроницаемы для частицы, вероятность обнаружить ее вне ямы вплоть до точек с координатами , равна нулю. Так как в одной точке пространства не может быть двух различных значений вероятности обнаружить частицу, то и внутри ямы у её границ вероятность обнаружить частицу также должна быть равна нулю. Это означает, что для –функции, квадрат модуля которой есть плотность вероятности, выполняются следующие граничные условия:

.

Используя первое граничное условие, имеем

,

следовательно,

, и .

Используя второе граничное условие, получаем

,

следовательно,

,

где квантовое число может принимать значения (значение ,допустимое с математической точки зрения, не имеет физического смысла, так как при этом –функция получается равной нулю внутри ямы для любых значений координаты ). Используя связь и (3.1), имеем

---