Файл: Методические указания к выполнению контрольной работы 3 для студентов зф и идо.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 202
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ангстрема.
Дано: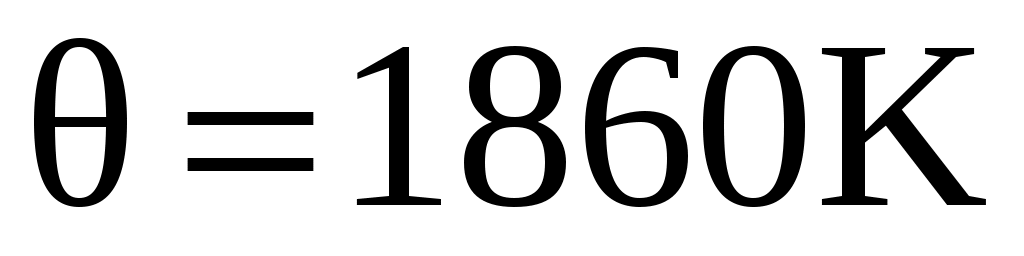 ;
;

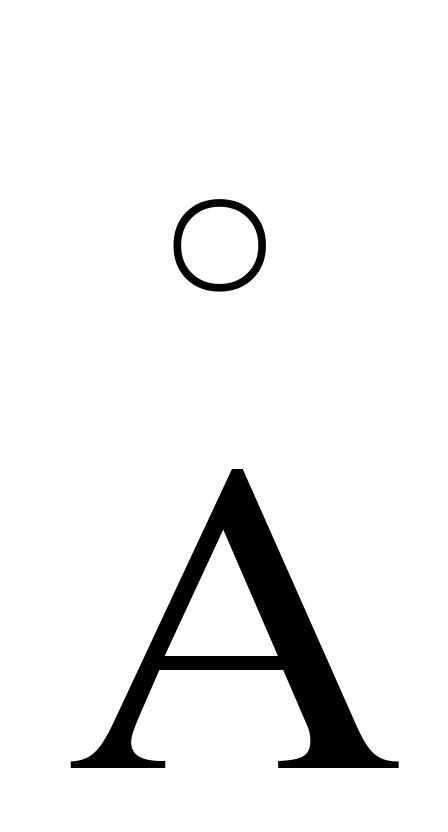
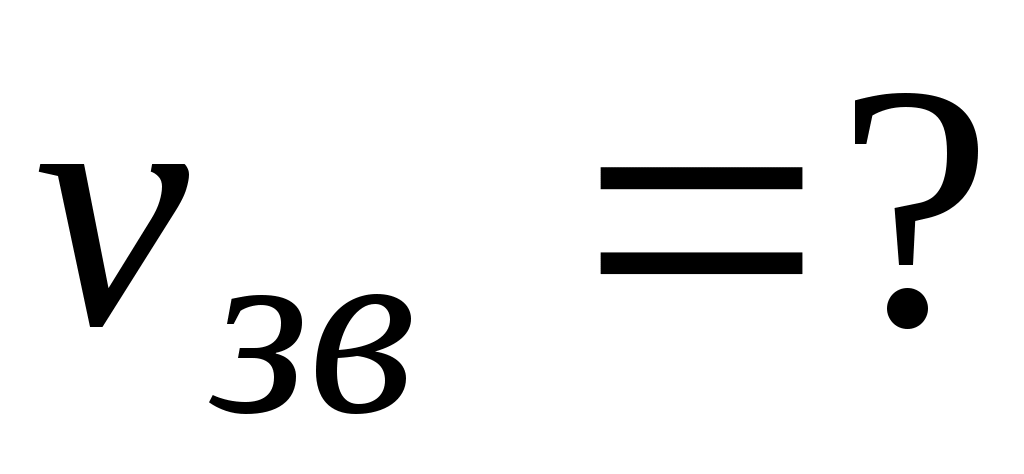
Решение. Определить скорость звука в алмазе можно с помощью выражения (4.3)
 .
.
Используя формулу (4.1) и учитывая, что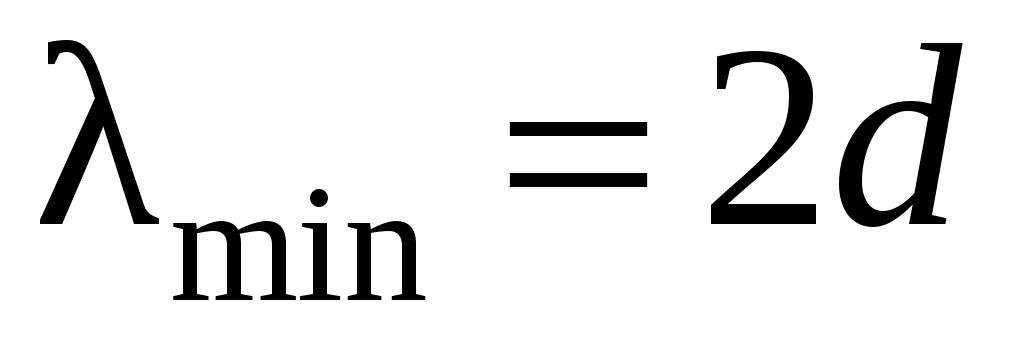 , получим
, получим
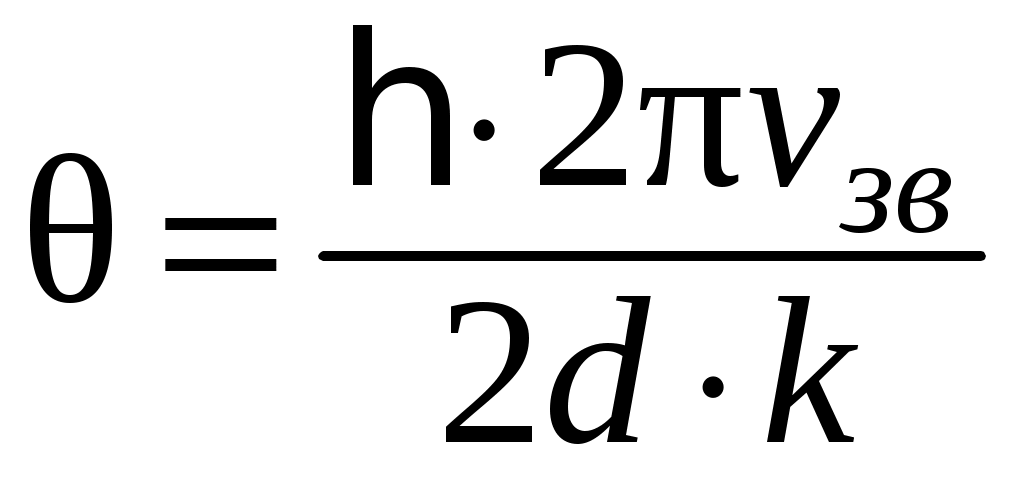 .
.
Выражаем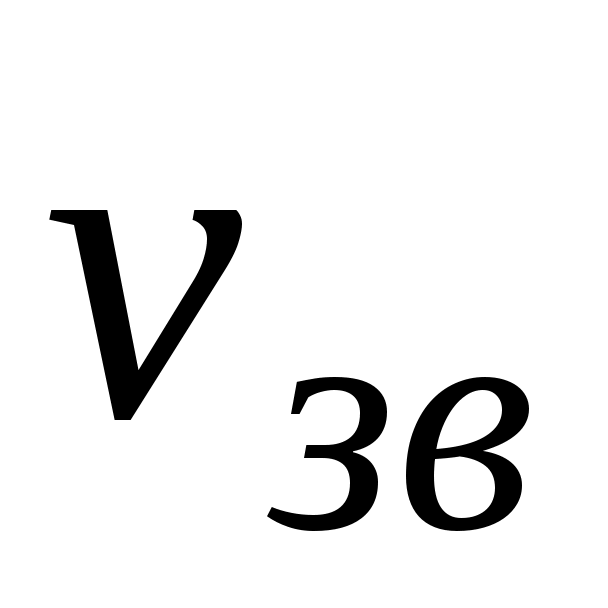 и проводим вычисления:
и проводим вычисления:
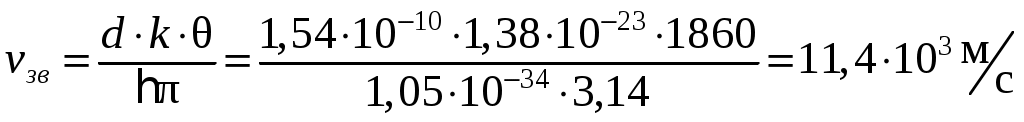 .
.
Проверим единицу измерения:
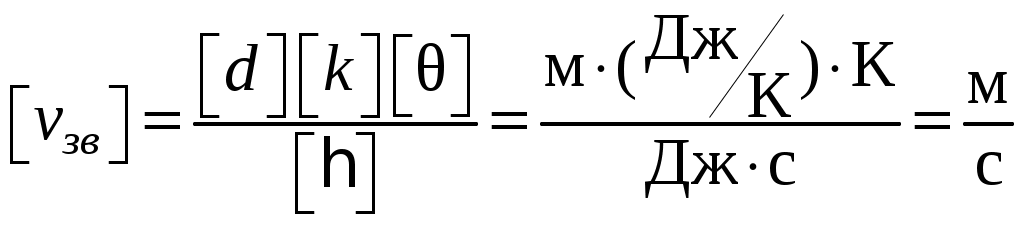
Ответ.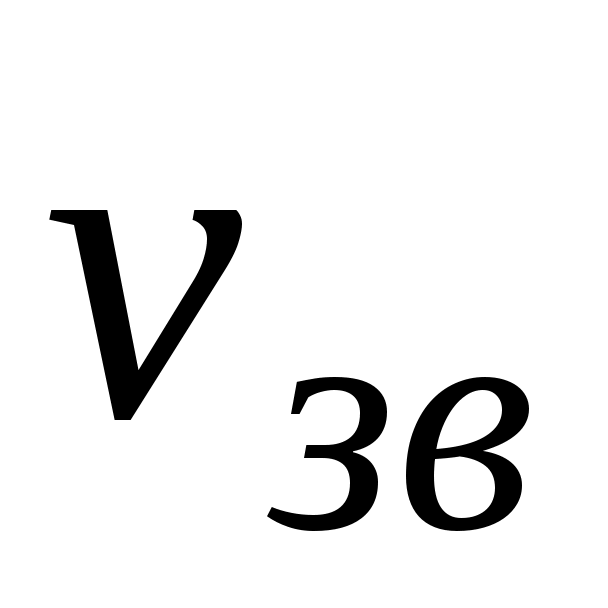 =11,4103 м/с.
=11,4103 м/с.
Темы 5, 6. КВАНТОВАЯ СТАТИСТИКА ФЕРМИ-ДИРАКА,
10
-23 эВ), для того чтобы перевести их на более высокие уровни. Достаточная для этого перехода энергия появляется при нагревании кристалла уже на 1 К. Даже небольшие электрические поля могут сообщать этим электронам дополнительную энергию, переводя их еще на более высокие уровни. Поэтому электроны могут ускоряться полем в таких веществах при любых температурах. В кристалле появляется упорядоченное движение электронов под действием поля, т. е. электрический ток. Кристалл с подобной схемой заполнения энергетических уровней представляет собой металл.
Если при температуре равной абсолютному нулю верхняя зона, на уровнях которой есть электроны (валентная зона), полностью укомплектована ими, а выше лежащая разрешенная зона (зона проводимости) не содержит электронов, то вещество не может проводить электрический ток. Однако если ширина запрещенной зоны невелика и составляет 1 ÷ 2 электрон-вольта (эВ) (случай (б)), энергия теплового движения атомов кристалла или энергия поглощенных им фотонов оказывается достаточной для того, чтобы перевести часть электронов из валентной зоны через запрещенную зону в зону проводимости. Одновременно станет возможным переход электронов валентной зоны на ее освободившиеся верхние уровни. Такое вещество называется собственным полупроводником.
электрон-вольта (эВ) (случай (б)), энергия теплового движения атомов кристалла или энергия поглощенных им фотонов оказывается достаточной для того, чтобы перевести часть электронов из валентной зоны через запрещенную зону в зону проводимости. Одновременно станет возможным переход электронов валентной зоны на ее освободившиеся верхние уровни. Такое вещество называется собственным полупроводником.
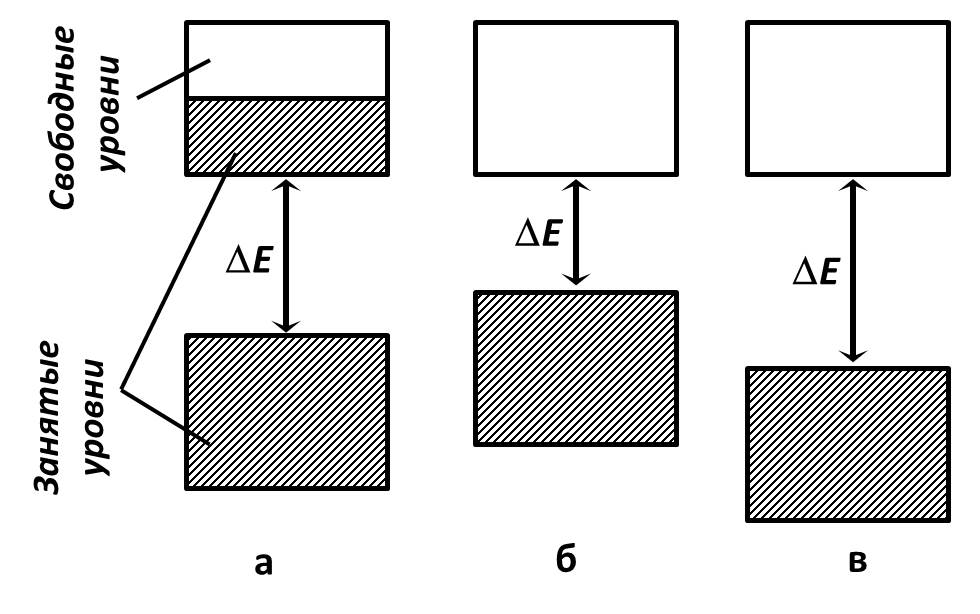
Рис 5.2. Заполнение энергетических зон при температуре Т = 0 К:
а – в металлах; б – в полупроводниках; в – диэлектриках
Если ширина запрещенной зоны велика (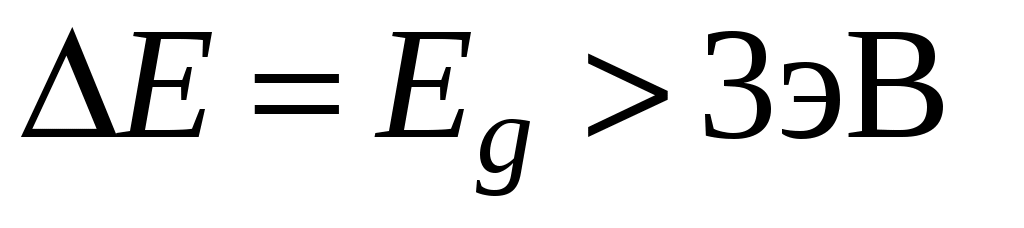 ), тепловое движение не может сообщить заметному числу электронов валентной зоны энергию, необходимую для перехода в свободную зону. В случае (в) кристалл является диэлектриком.
), тепловое движение не может сообщить заметному числу электронов валентной зоны энергию, необходимую для перехода в свободную зону. В случае (в) кристалл является диэлектриком.
3. Электроны проводимости в металле можно рассматривать как газ свободных частиц при условии, что их взаимодействие с кристаллической решеткой учитывается путем введения для электронов вместо реальной массы, так называемой эффективной массы.
Количество различных квантовых состояний, приходящееся на единичный интервал энергий, для кристалла единичного объема равно [1,4]
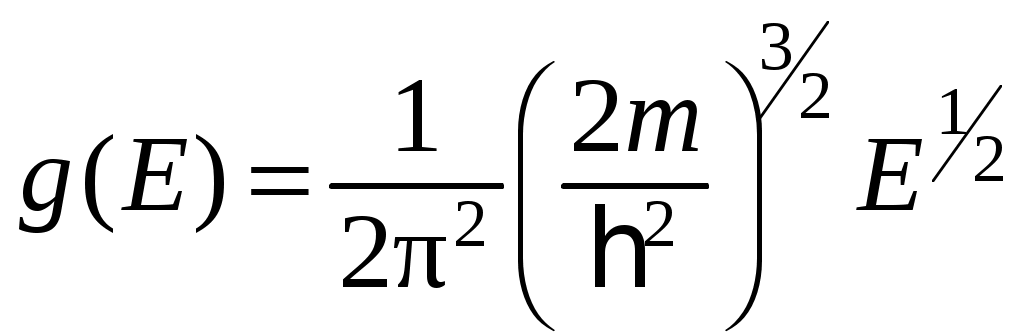
. (5.1)
Величина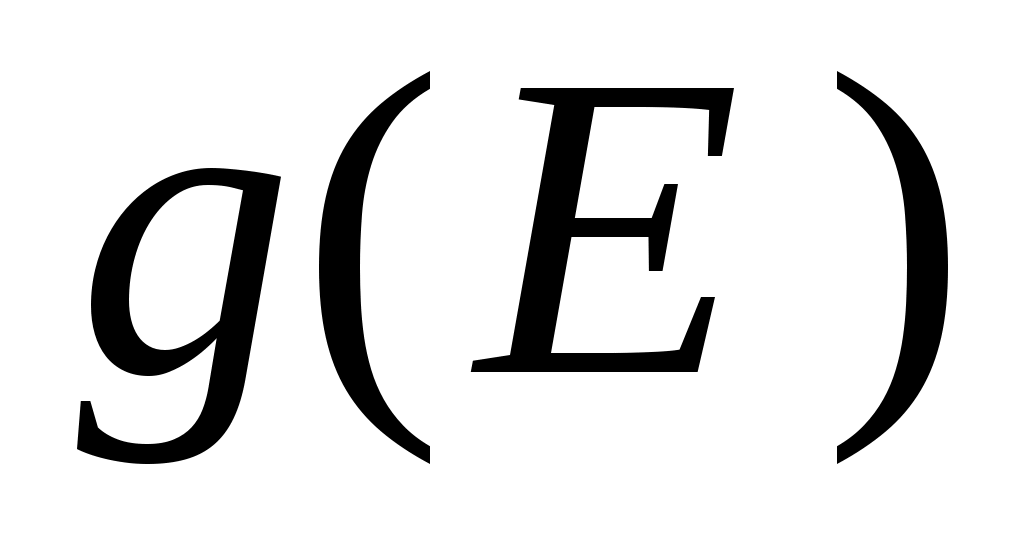 называется плотностью состояний.
называется плотностью состояний.
Распределение свободных электронов по квантовым состояниям описывается функцией Ферми-Дирака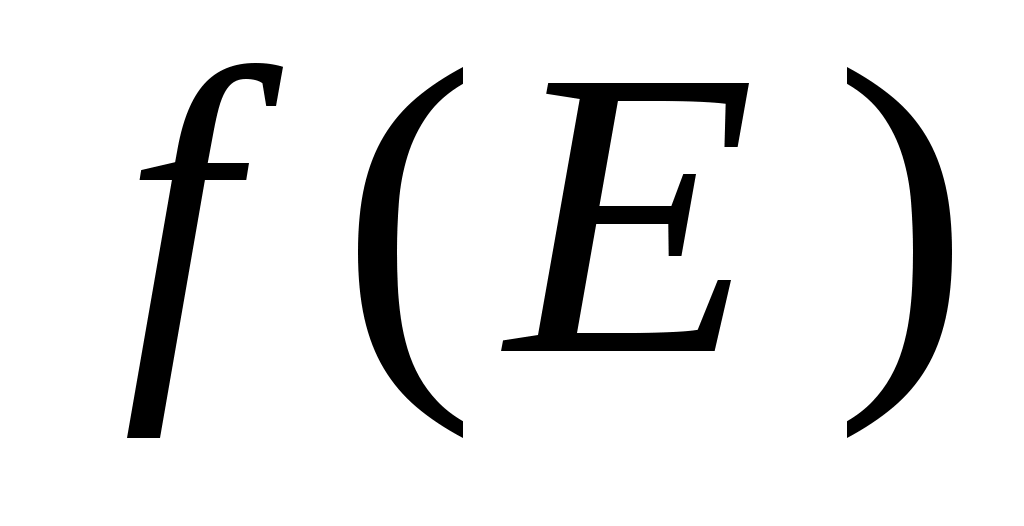 . Эта функция определяет вероятность того, что состояние с данной энергией
. Эта функция определяет вероятность того, что состояние с данной энергией  занято электроном
занято электроном
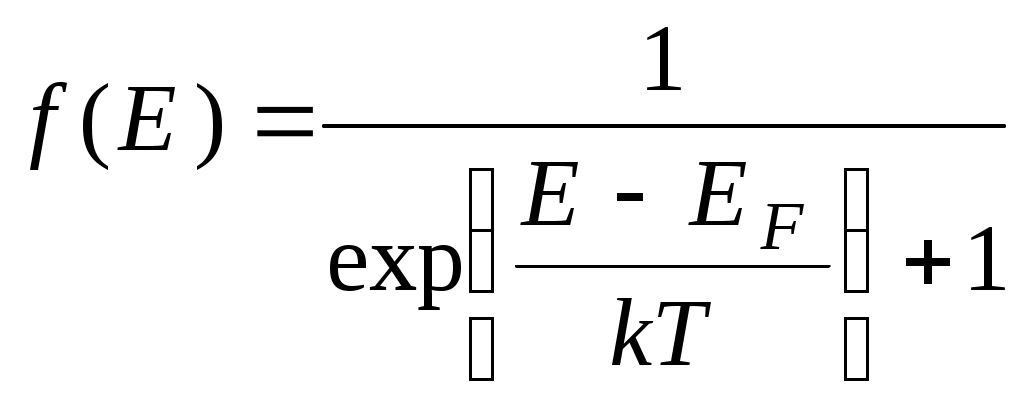 . (5.2)
. (5.2)
В формуле (5.2)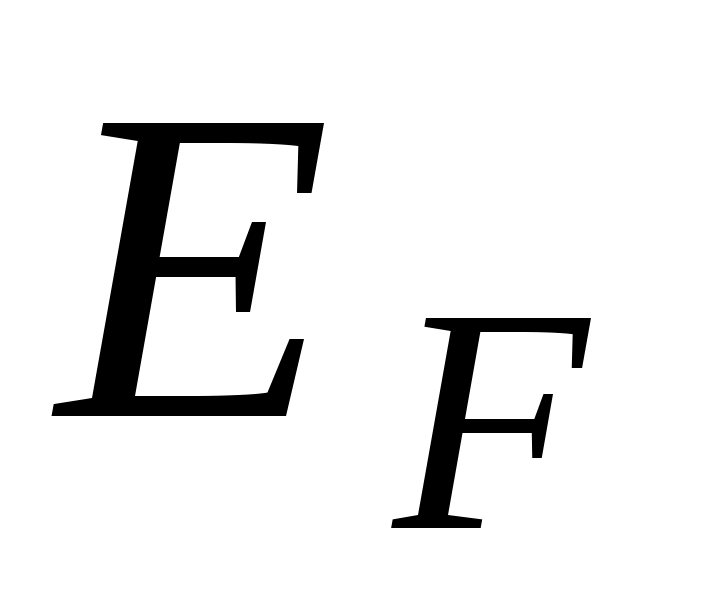 – энергия Ферми. В металле, при
– энергия Ферми. В металле, при 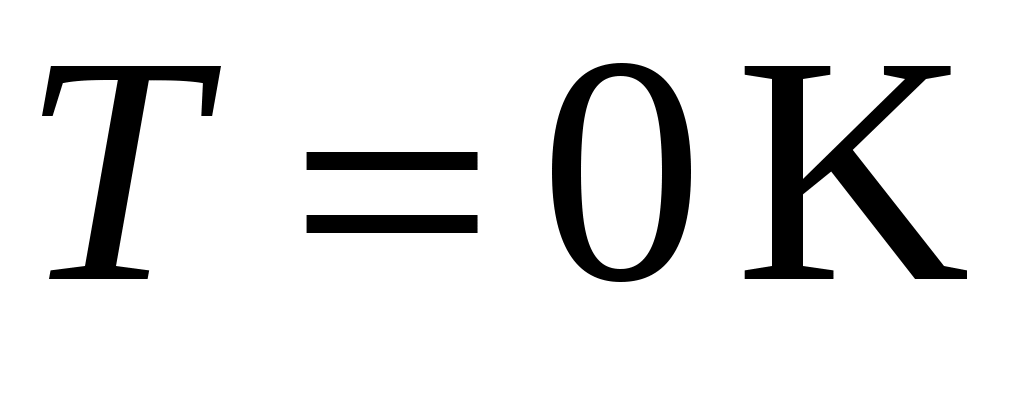 , в валентной зоне все состояния вплоть до
, в валентной зоне все состояния вплоть до 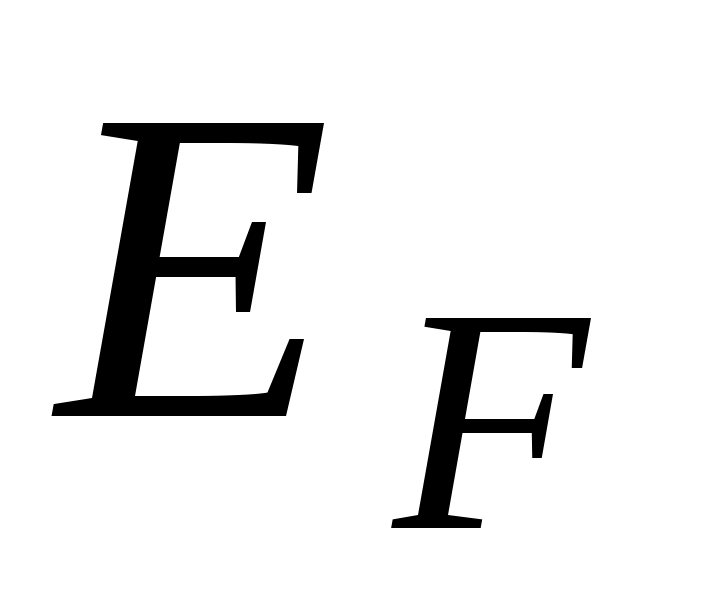 заняты электронами, а выше
заняты электронами, а выше 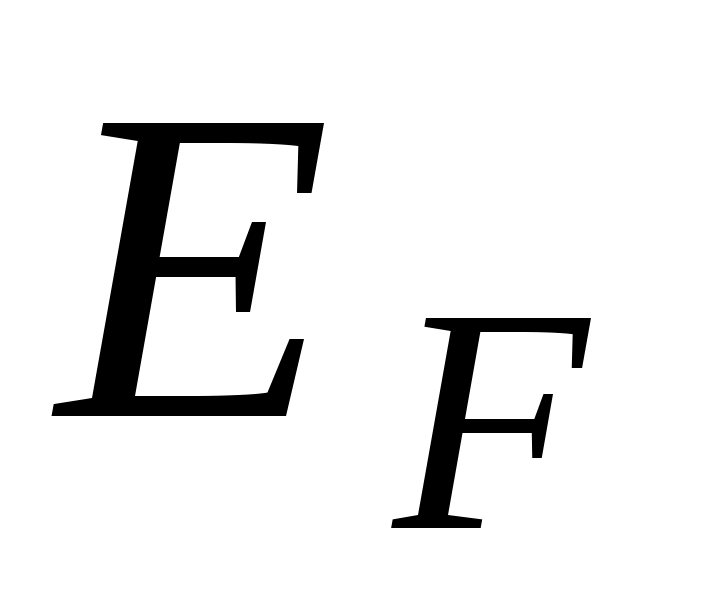 – свободны. Таким образом, при температуре
– свободны. Таким образом, при температуре 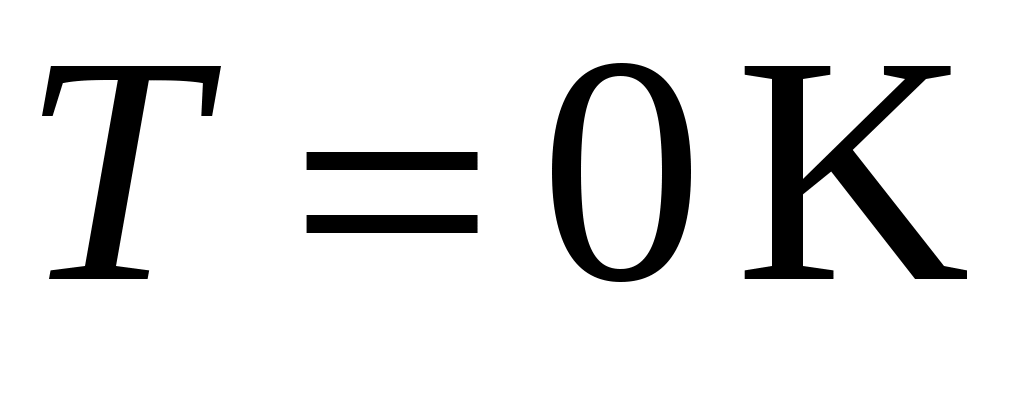 , вероятность заполнения электронами состояний с энергией
, вероятность заполнения электронами состояний с энергией  <
<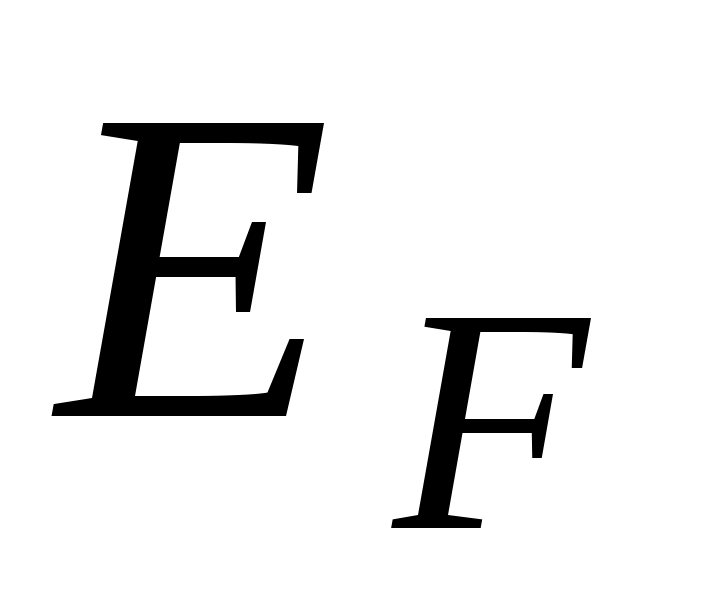 равна единице, а вероятность заполнения состояний с энергией
равна единице, а вероятность заполнения состояний с энергией  >
>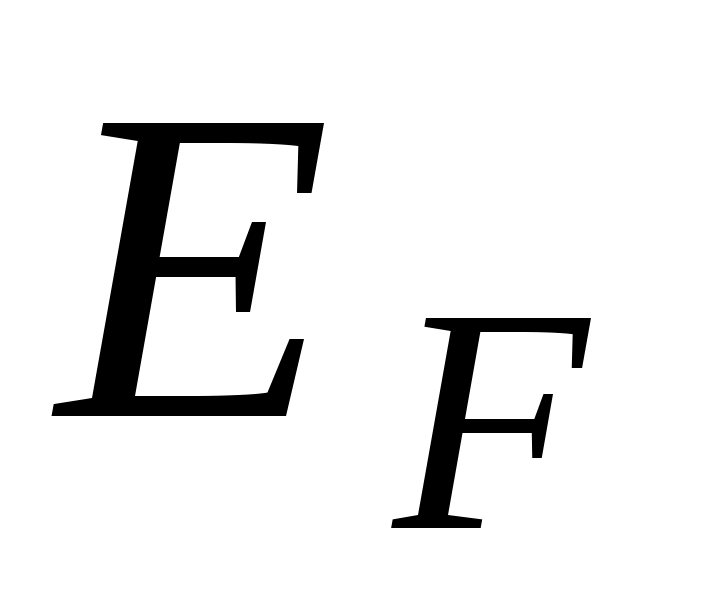 равна нулю (рис.5.3,а).
равна нулю (рис.5.3,а).
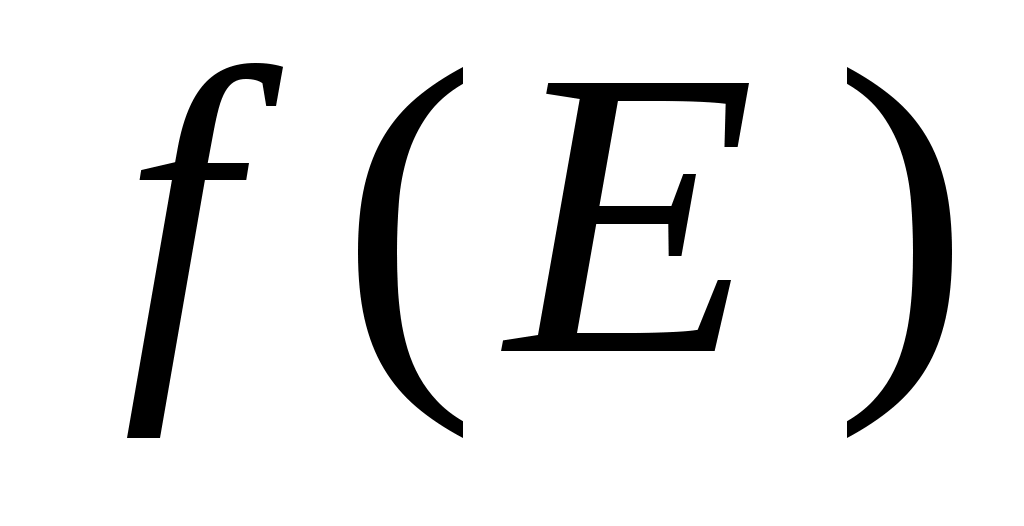 =1, если
=1, если  <
<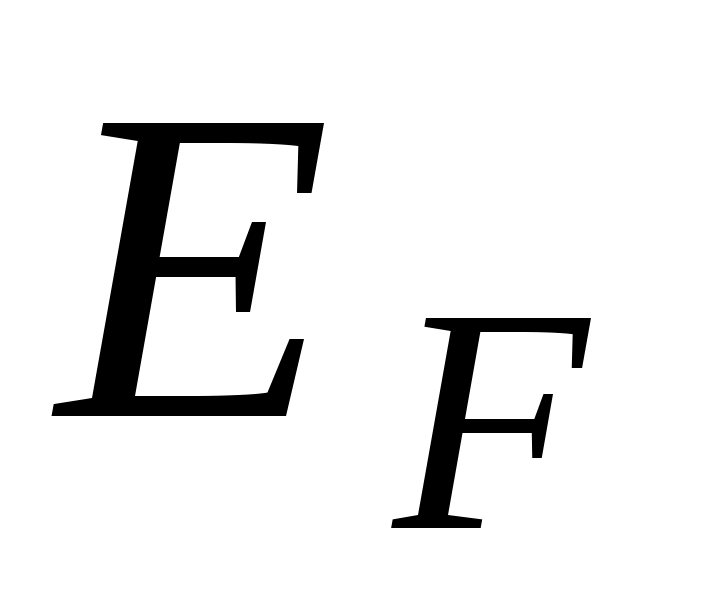 ,
, 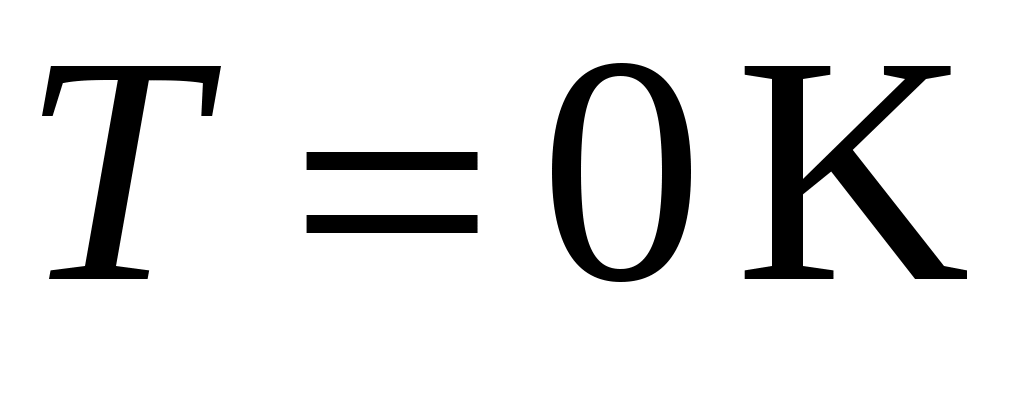 (5.3)
(5.3)
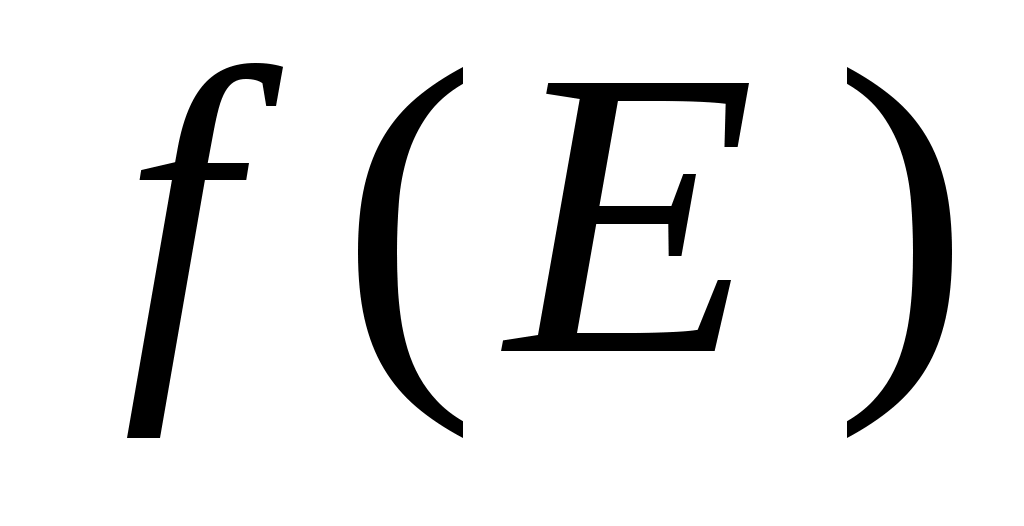 =0, если
=0, если  >
>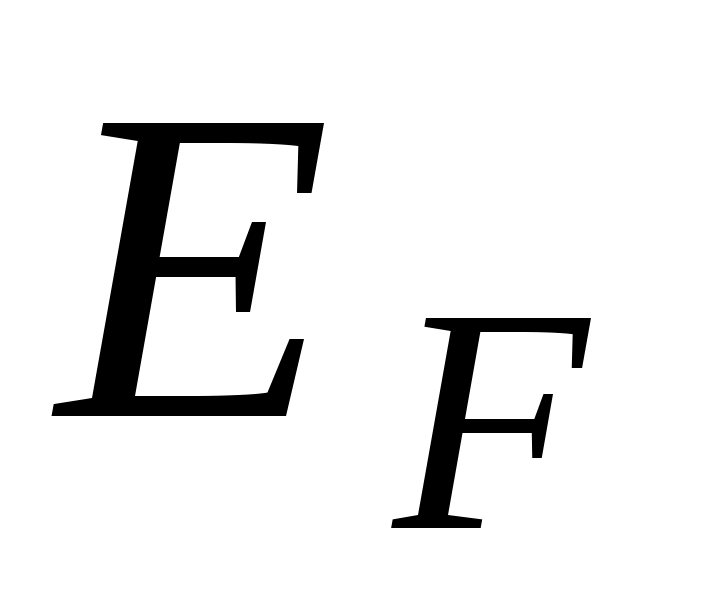 ,
, 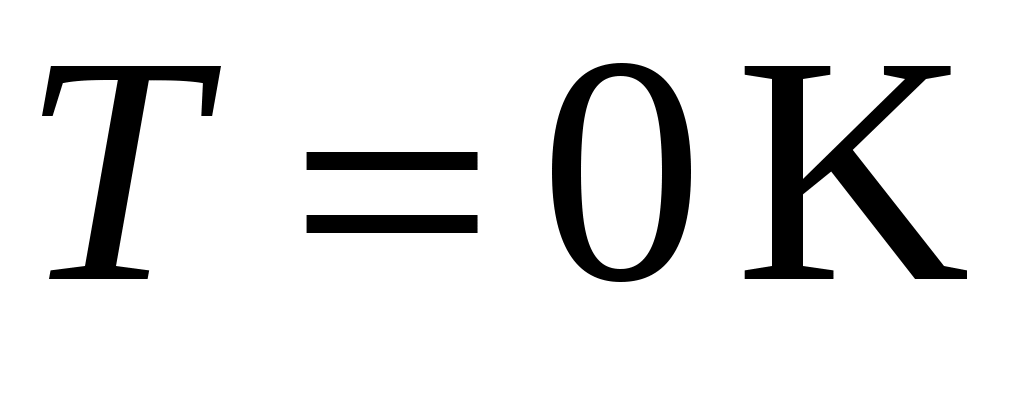 .
.
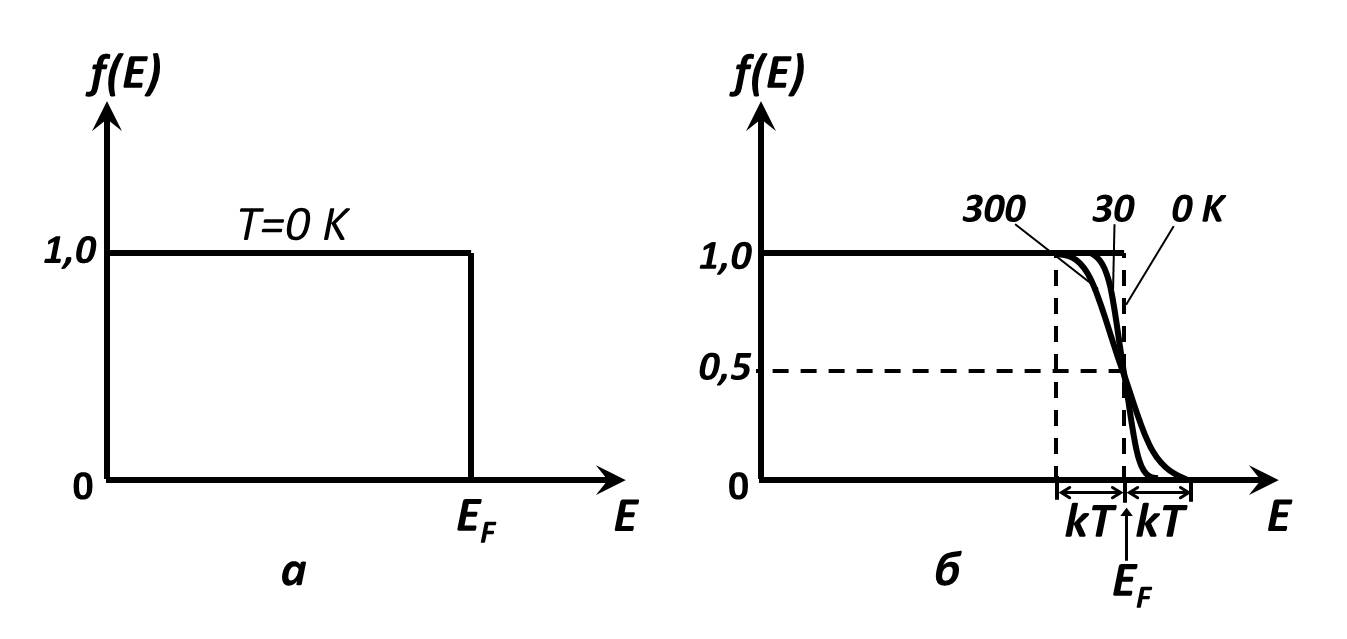
Рис. 5.3. Функция распределения Ферми-Дирака:
а – при температуре Т = 0 К; б – при Т 0К
Величины и
и  для очень узкого диапазона энергий
для очень узкого диапазона энергий 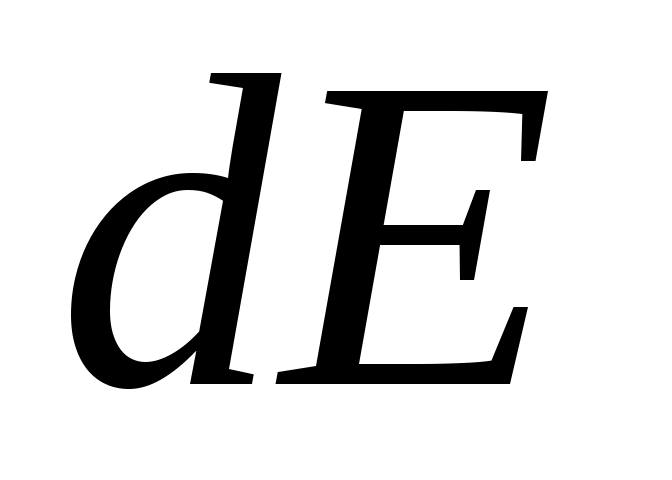 можно считать постоянными. Тогда число электронов, имеющих энергию в интервале от
можно считать постоянными. Тогда число электронов, имеющих энергию в интервале от  до
до  +
+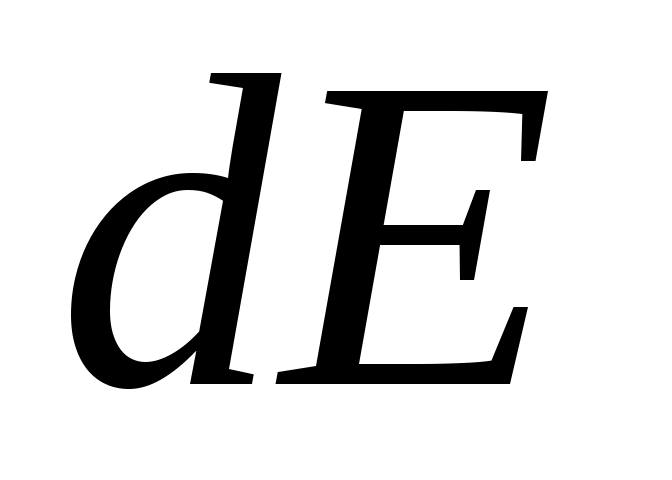 , в единице объема кристалла
, в единице объема кристалла
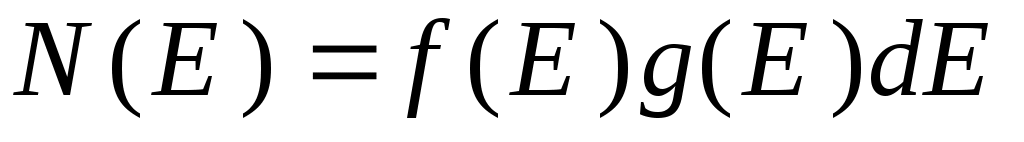 . (5.4)
. (5.4)
Тогда в интервале энергий от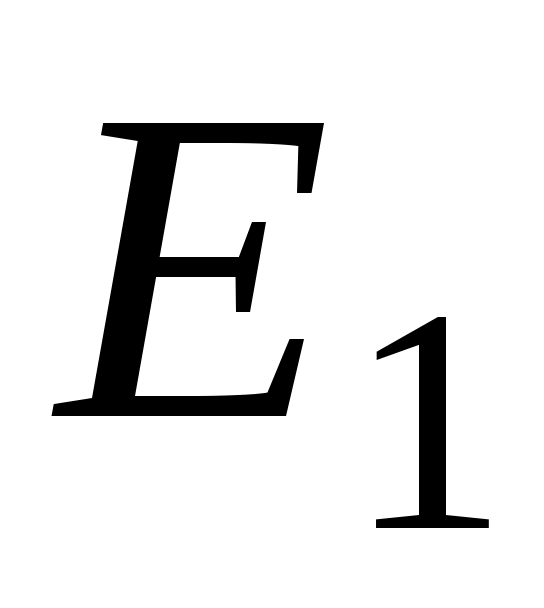 до
до 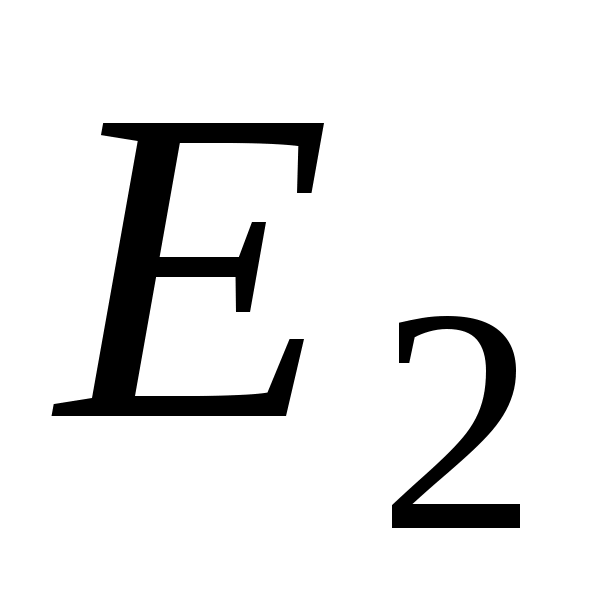
 количество частиц определяется как
количество частиц определяется как
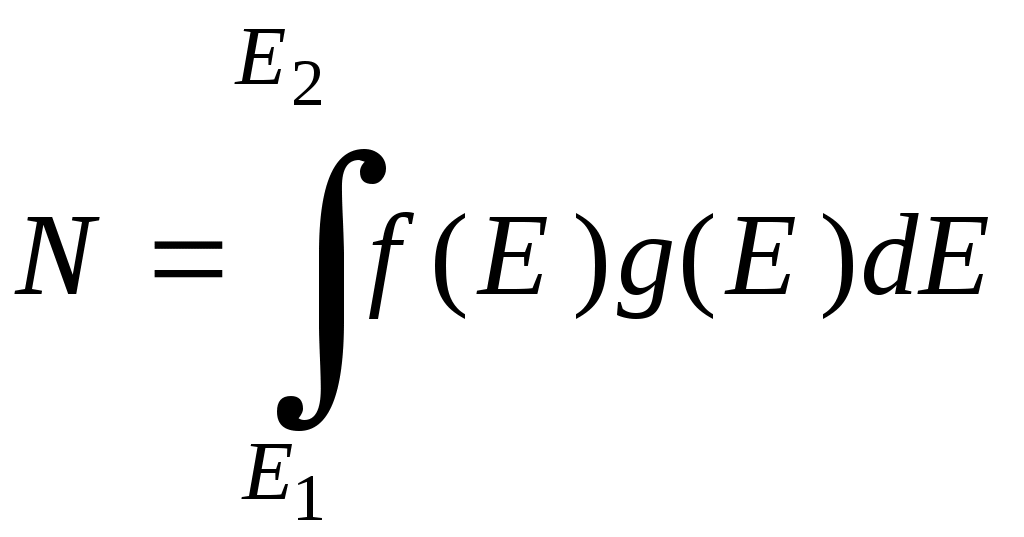 .
.
Используя это выражение, получим формулу для концентрации электронов в металле при температуре
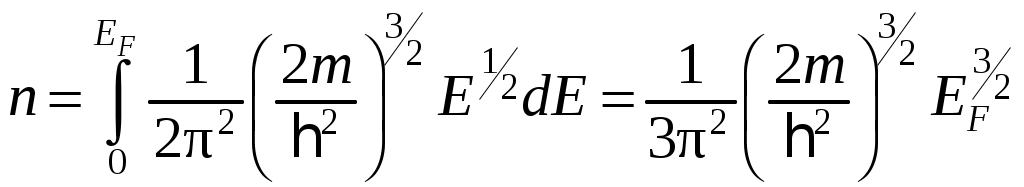 . (5.5)
. (5.5)
Получим зависимость энергии Ферми от концентрации электронов в валентной зоне при температуре
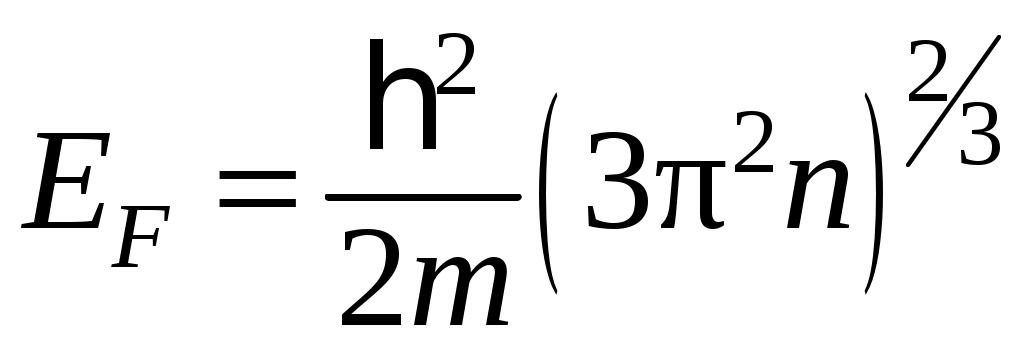 . (5.6)
. (5.6)
При повышении температуры электроны получают возможность переходить на более высокие энергетические уровни. Но повышать свою энергию могут только электроны, находящиеся вблизи уровня Ферми , так как ниже
, так как ниже  все состояния заняты. Тепловая энергия, получаемая электронами при
все состояния заняты. Тепловая энергия, получаемая электронами при 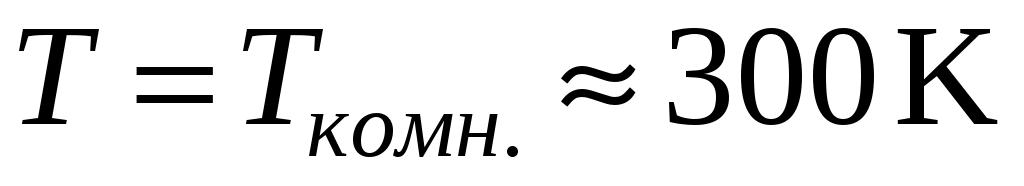 , имеет порядок
, имеет порядок 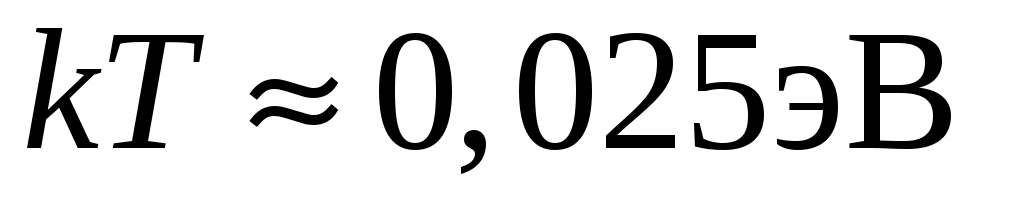
Дано:
Решение. Определить скорость звука в алмазе можно с помощью выражения (4.3)
Используя формулу (4.1) и учитывая, что
Выражаем
Проверим единицу измерения:
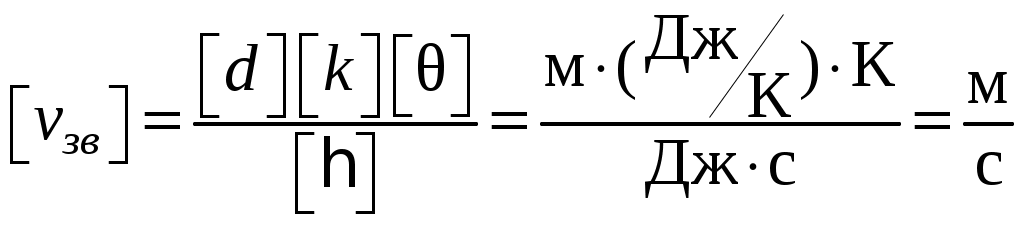
Ответ.
Темы 5, 6. КВАНТОВАЯ СТАТИСТИКА ФЕРМИ-ДИРАКА,
ЭЛЕКТРОПРОВОДНОСТЬ ТВЕРДЫХ ТЕЛ
1. В изолированных атомах электроны находятся в дискретных энергетических состояниях. У одиночных атомов одного элемента, расположенных на таких больших расстояниях 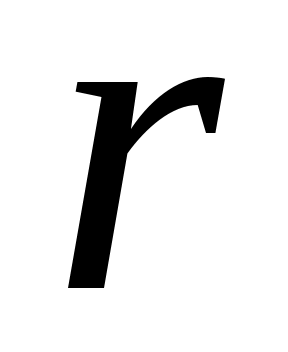 , что взаимодействием между ними можно пренебречь (
, что взаимодействием между ними можно пренебречь ( , где
, где  – постоянная кристаллической решетки), энергия соответствующих энергетических уровней абсолютно одинакова. Так как потенциальная энергия взаимодействия электрона с ядром атома
– постоянная кристаллической решетки), энергия соответствующих энергетических уровней абсолютно одинакова. Так как потенциальная энергия взаимодействия электрона с ядром атома 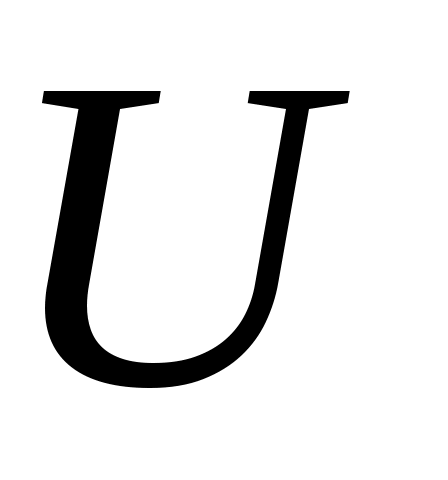 обратно пропорциональна расстоянию между ними
обратно пропорциональна расстоянию между ними 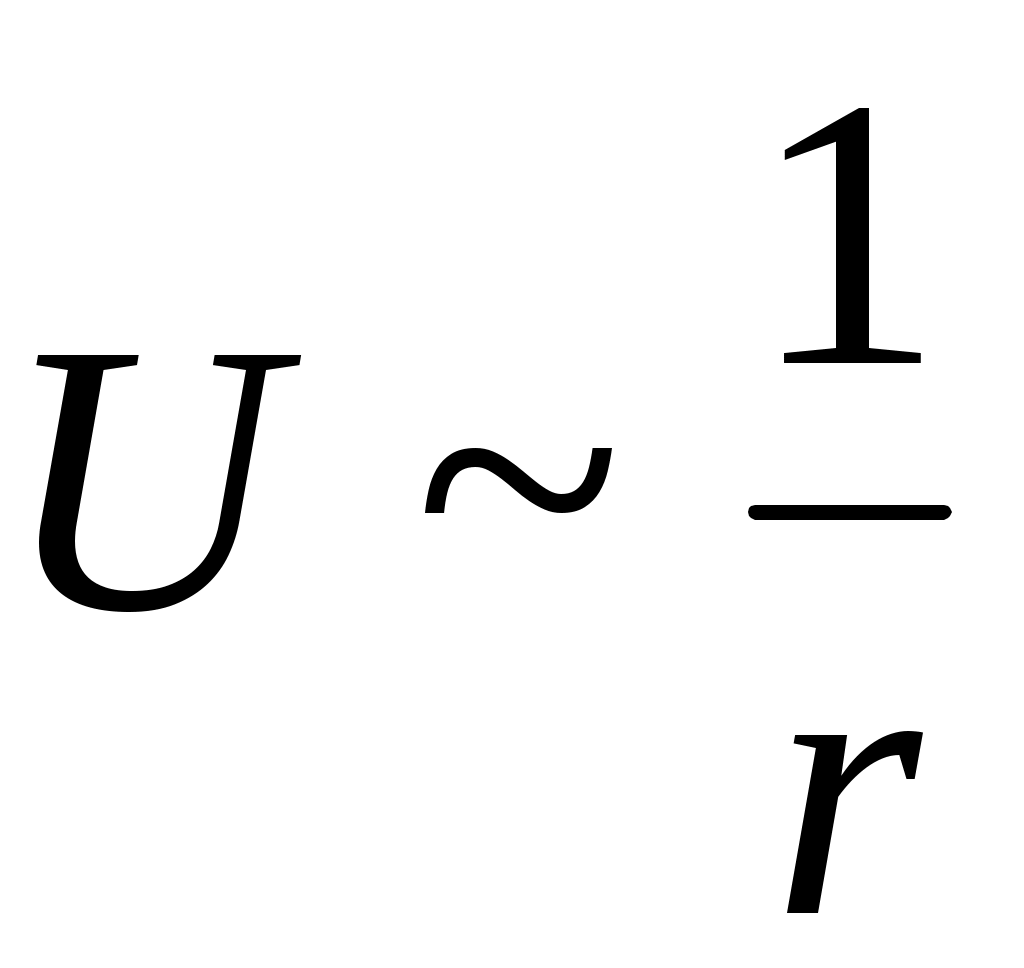 ,то атом является для электрона потенциальной ямой, внутри которой электроны находятся на определенных энергетических уровнях. При этом между соседними атомами имеется высокий и широкий потенциальный барьер.
,то атом является для электрона потенциальной ямой, внутри которой электроны находятся на определенных энергетических уровнях. При этом между соседними атомами имеется высокий и широкий потенциальный барьер.
При сближении атомов взаимодействие между ними растет. При этом для всех электронов в атомах уменьшается как ширина (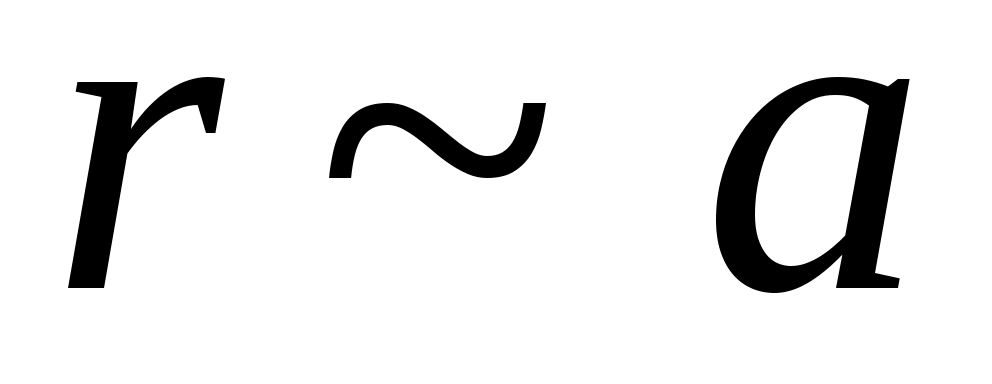 ), так и высота потенциального барьера, причем для валентных электронов высота потенциального барьера может стать ниже их энергетического уровня в изолированном атоме. В этом случае валентные электроны получают возможность легко переходить от одного атома к другому. Такие обобществленные кристаллом электроны называют свободными, а их совокупность – электронным газом.
), так и высота потенциального барьера, причем для валентных электронов высота потенциального барьера может стать ниже их энергетического уровня в изолированном атоме. В этом случае валентные электроны получают возможность легко переходить от одного атома к другому. Такие обобществленные кристаллом электроны называют свободными, а их совокупность – электронным газом.
Взаимодействие атомов в кристалле существенно меняет структуру энергетических уровней электронов. При сближении 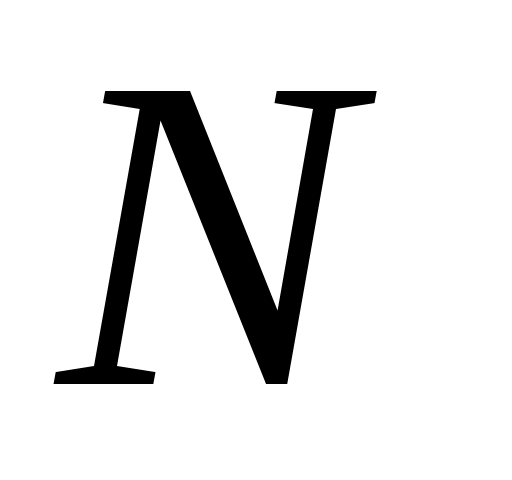 атомов каждый энергетический уровень изолированного атома расщепляется на
атомов каждый энергетический уровень изолированного атома расщепляется на 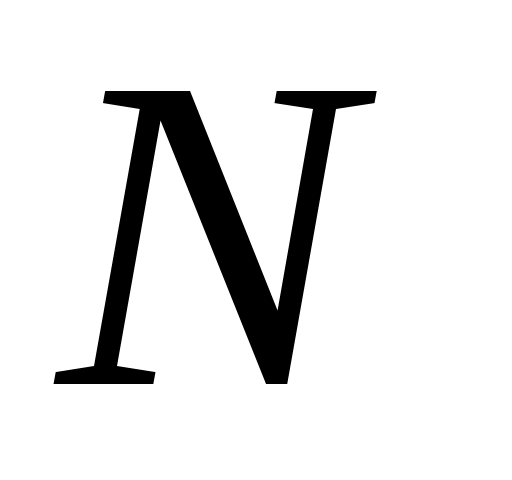 очень близко расположенных уровней, образующих зону разрешенных энергий. Разрешенные зоны отделены друг от друга запрещенными зонами.
очень близко расположенных уровней, образующих зону разрешенных энергий. Разрешенные зоны отделены друг от друга запрещенными зонами.
Расщепление разных уровней не одинаково. Наибольшее расщепление испытывают высоко расположенные уровни как занятые, так и не занятые электронами. Поэтому зона, соответствующая валентным электронам, оказывается широкой. Для электронов, расположенных на нижних энергетических уровнях атома, потенциальный барьер, после сближения, остается очень трудно проходимым, поэтому соответствующие энергетические уровни практически не расщепляются (рис. 5.1). Следует отметить, что ширина зон не зависит от размеров кристалла. Поэтому, чем больше атомов содержит кристалл, тем теснее располагаются уровни внутри разрешенной зоны. Для кристалла, состоящего, например, из 1023 атомов, расстояние между соседними уровнями зоны составляет примерно 10-23 эВ.
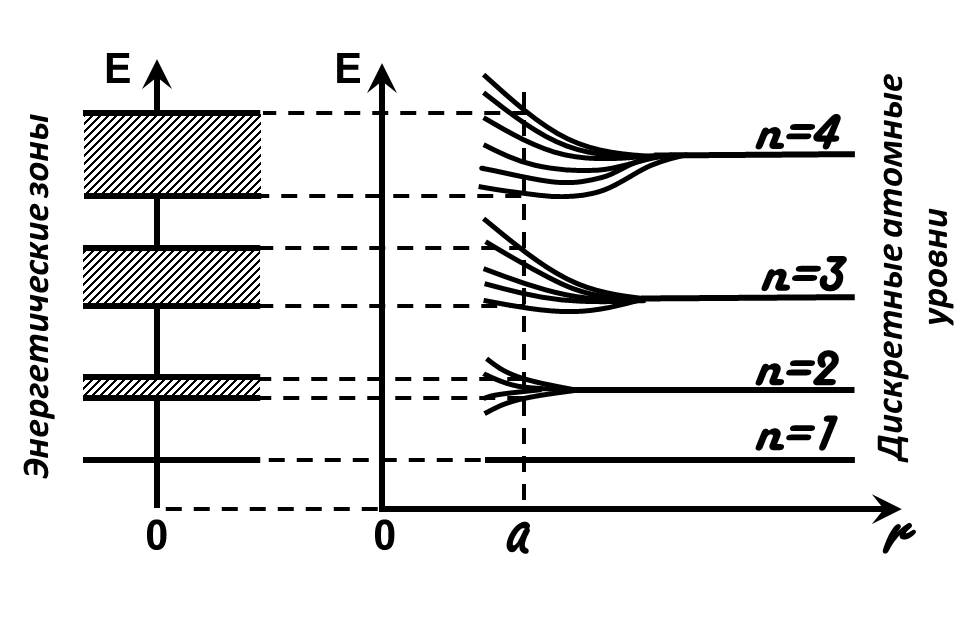
Рис. 5.1. Схема образования энергетических зон при сближении атомов
(а – постоянная решетки кристалла)
2. Существование энергетических зон позволяет объяснить с единой точки зрения различие электрофизических характеристик металлов, полупроводников и диэлектриков.
Электрические свойства твердых тел зависят от характера заполнения электронами разрешенных и от ширины запрещенных энергетических зон. Заполнение электронами энергетических уровней в разрешенной зоне осуществляется в соответствии с принципом Паули, согласно которому в системе не может быть даже двух электронов с одинаковым набором всех квантовых чисел. В атоме этими числами являются:  – главное квантовое число,
– главное квантовое число, 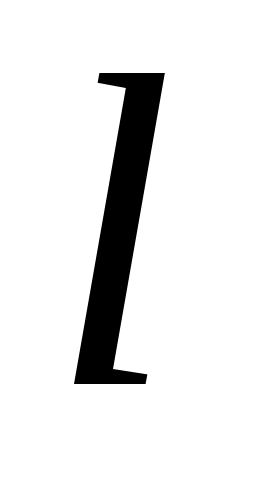 – орбитальное,
– орбитальное, 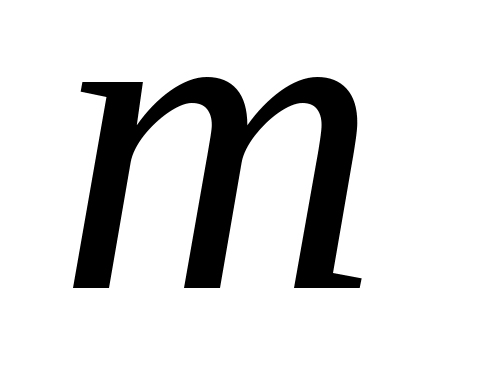 – магнитное,
– магнитное, 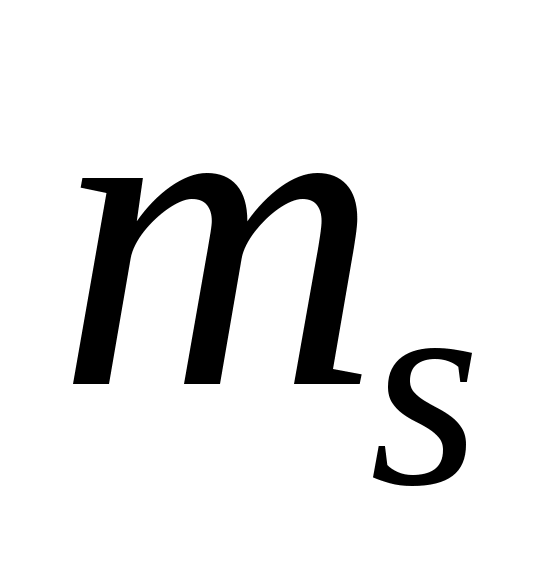 – магнитное спиновое квантовое число.
– магнитное спиновое квантовое число.
Возможны три случая (рис 5.2). В случае (а) электроны заполняют валентную зону не полностью. Поэтому достаточно сообщить электронам, находящимся на верхних уровнях, совсем небольшую энергию (
10
-23 эВ), для того чтобы перевести их на более высокие уровни. Достаточная для этого перехода энергия появляется при нагревании кристалла уже на 1 К. Даже небольшие электрические поля могут сообщать этим электронам дополнительную энергию, переводя их еще на более высокие уровни. Поэтому электроны могут ускоряться полем в таких веществах при любых температурах. В кристалле появляется упорядоченное движение электронов под действием поля, т. е. электрический ток. Кристалл с подобной схемой заполнения энергетических уровней представляет собой металл.
Если при температуре равной абсолютному нулю верхняя зона, на уровнях которой есть электроны (валентная зона), полностью укомплектована ими, а выше лежащая разрешенная зона (зона проводимости) не содержит электронов, то вещество не может проводить электрический ток. Однако если ширина запрещенной зоны невелика и составляет 1 ÷ 2

Рис 5.2. Заполнение энергетических зон при температуре Т = 0 К:
а – в металлах; б – в полупроводниках; в – диэлектриках
Если ширина запрещенной зоны велика (
3. Электроны проводимости в металле можно рассматривать как газ свободных частиц при условии, что их взаимодействие с кристаллической решеткой учитывается путем введения для электронов вместо реальной массы, так называемой эффективной массы.
Количество различных квантовых состояний, приходящееся на единичный интервал энергий, для кристалла единичного объема равно [1,4]
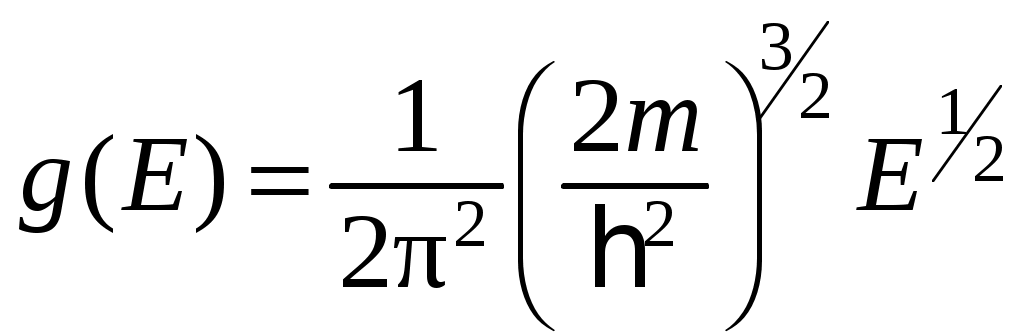
. (5.1)
Величина
Распределение свободных электронов по квантовым состояниям описывается функцией Ферми-Дирака
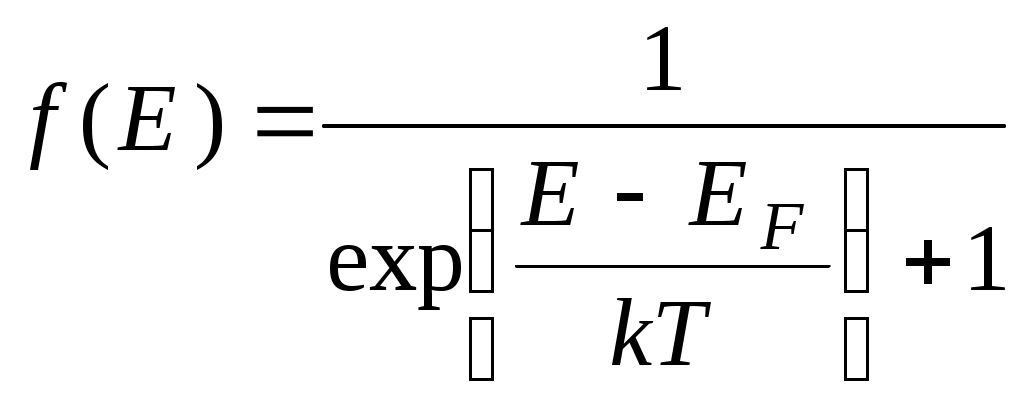 . (5.2)
. (5.2)В формуле (5.2)

Рис. 5.3. Функция распределения Ферми-Дирака:
а – при температуре Т = 0 К; б – при Т 0К
Величины
Тогда в интервале энергий от
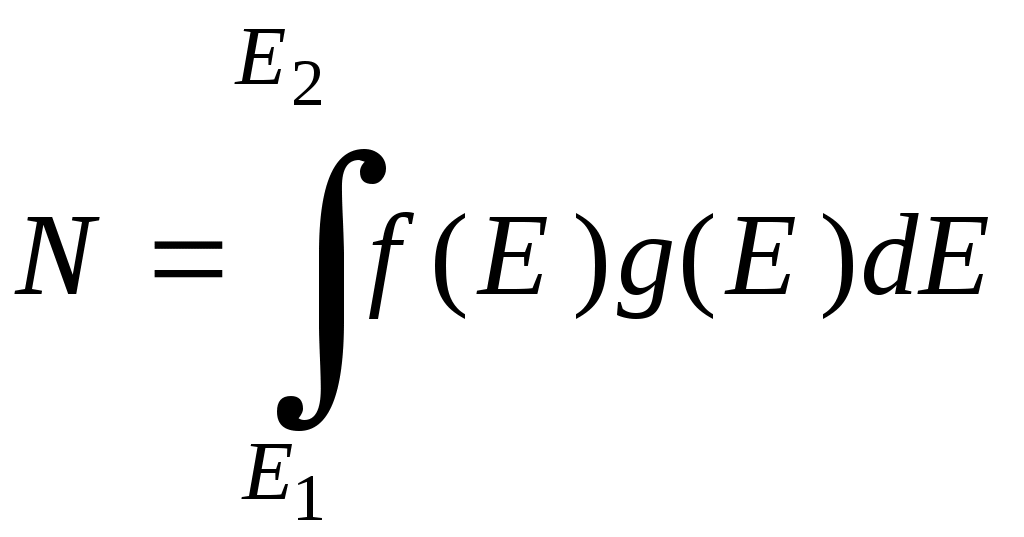 .
.Используя это выражение, получим формулу для концентрации электронов в металле при температуре
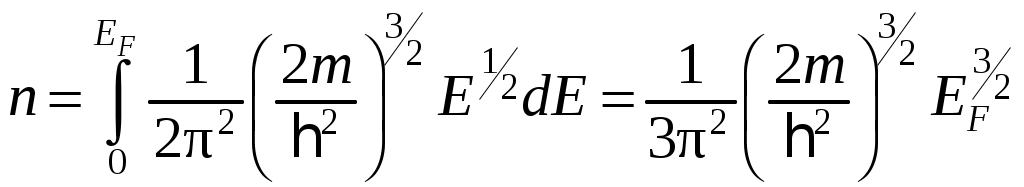 . (5.5)
. (5.5)Получим зависимость энергии Ферми от концентрации электронов в валентной зоне при температуре
При повышении температуры электроны получают возможность переходить на более высокие энергетические уровни. Но повышать свою энергию могут только электроны, находящиеся вблизи уровня Ферми