Файл: Методические указания к выполнению контрольной работы 3 для студентов зф и идо.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 207
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Таким образом, при движении частицы-волны в ограниченной области пространства уравнение Шредингера имеет решение лишь для определенных (квантовых) значений полной энергии. Они называются собственными значениями, а соответствующие им –функции – собственными функциями:
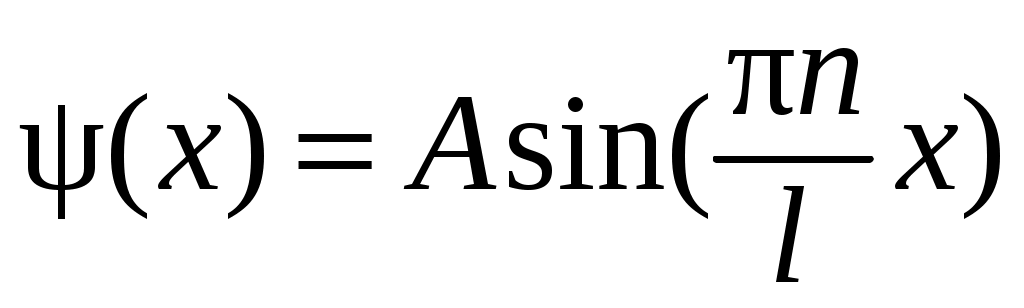 .
.
Вероятность и плотность вероятности обнаружить частицу в бесконечно малой области одномерного пространства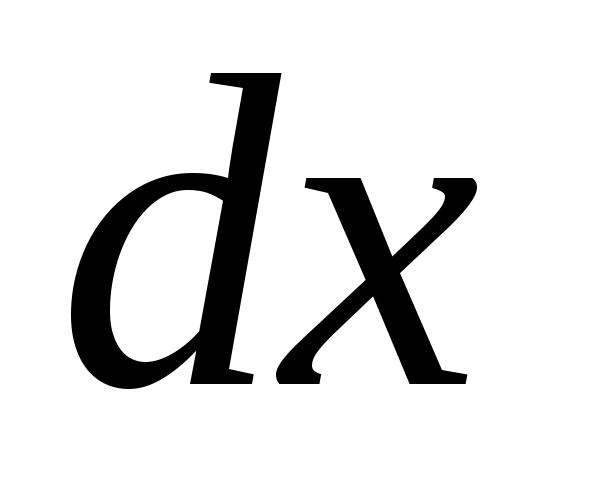 внутри ямы, следовательно, равны
внутри ямы, следовательно, равны
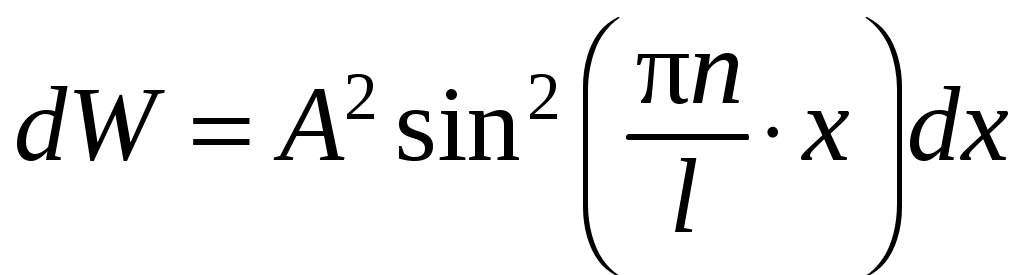 ,
, 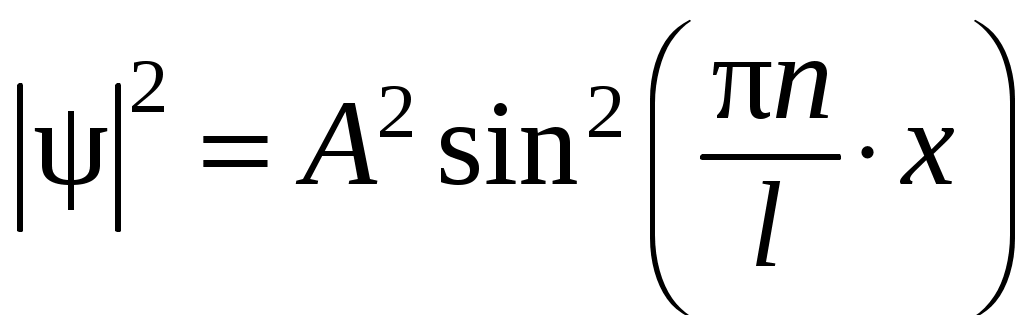 .
.
Г
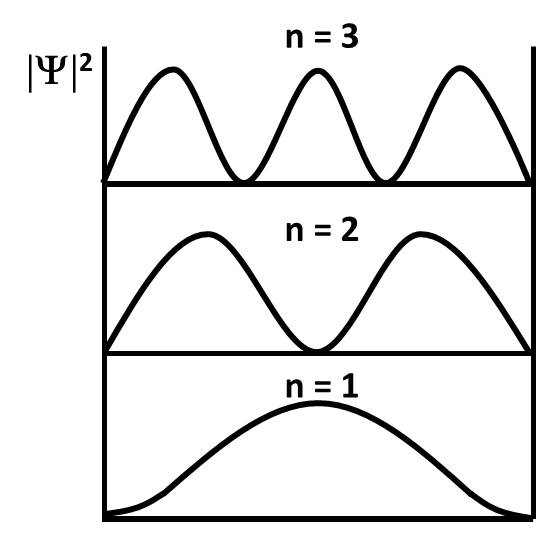
Рис 3.2. Плотность веро-ятности нахождения
частицы в яме
рафики зависимости плотности вероятности от координаты для различных значений квантового числа показаны на рис. 3.2.
показаны на рис. 3.2.
Задача. Собственные функции, описывающие состояние частицы, находящейся в одномерной бесконечно глубокой потенциальной яме, имеют вид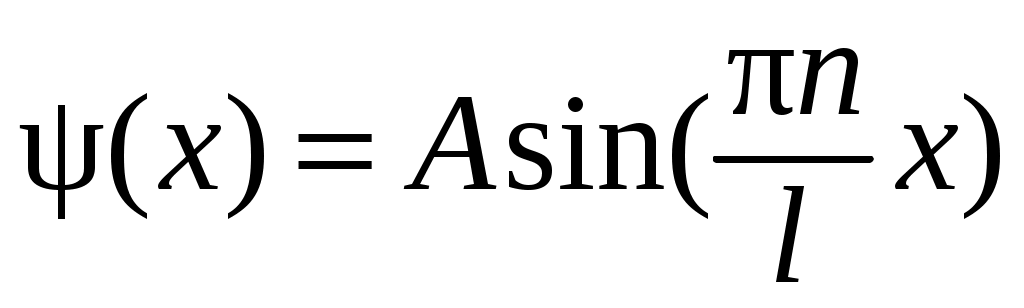 . Используя условие нормировки, определите постоянную
. Используя условие нормировки, определите постоянную  .
.
Рис. 3.2.
Плотность вероятности нахождения частицы в яме
Решение. Поскольку частица, согласно условию задачи, находится в некотором месте пространства, то вероятность обнаружить ее в диапазоне значений координаты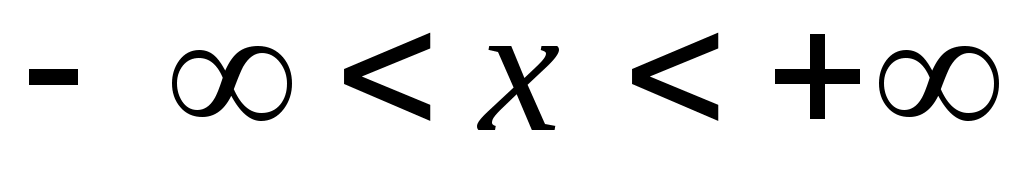 равна единице
равна единице
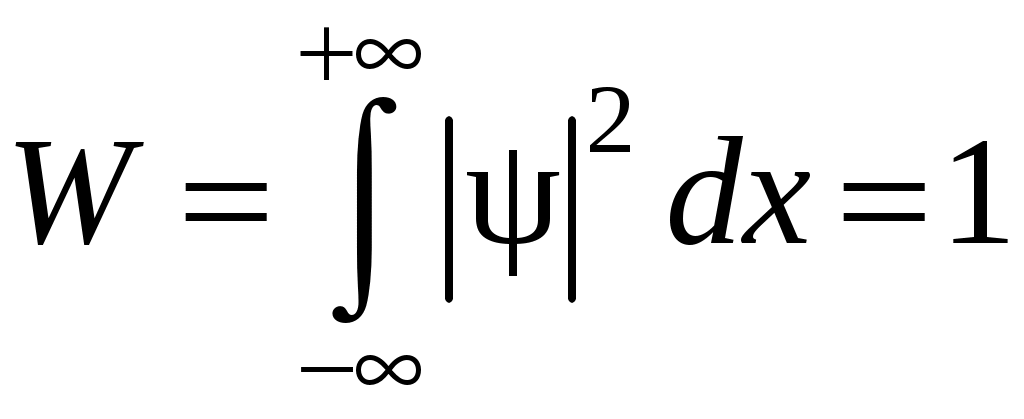 .
.
Область интегрирования можно ограничить диапазоном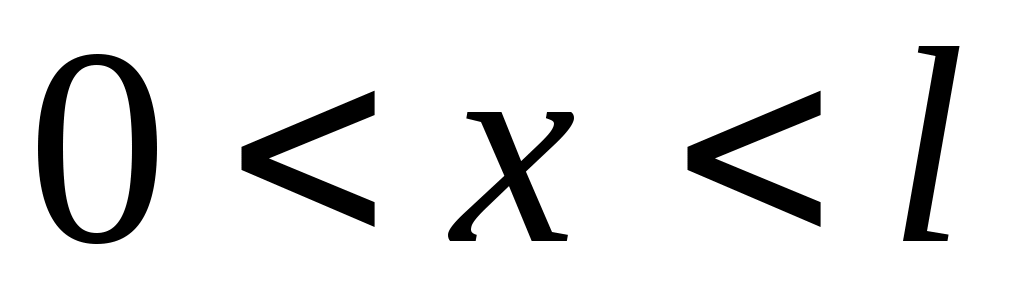 , так как вне этого диапазона -функция равна нулю
, так как вне этого диапазона -функция равна нулю
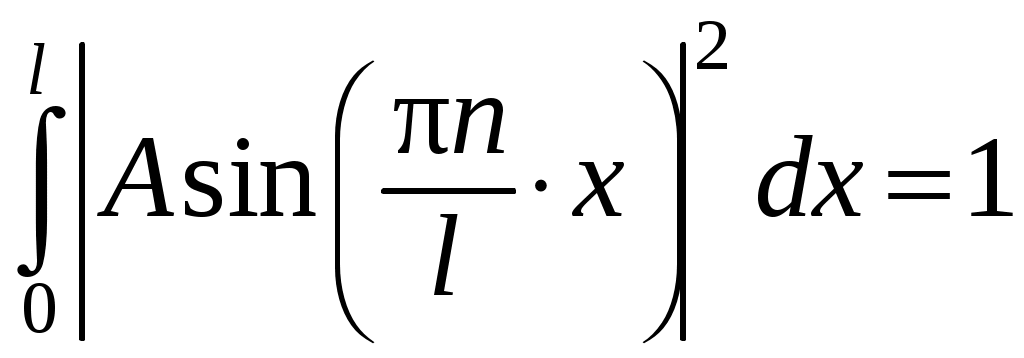 ,
, 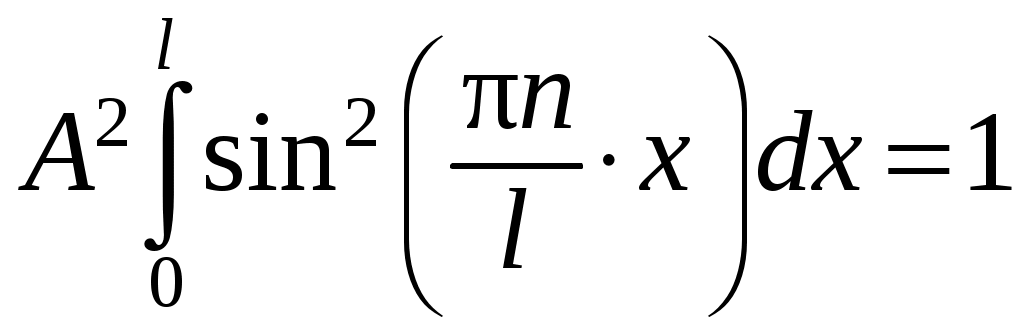 .
.
Отсюда следует
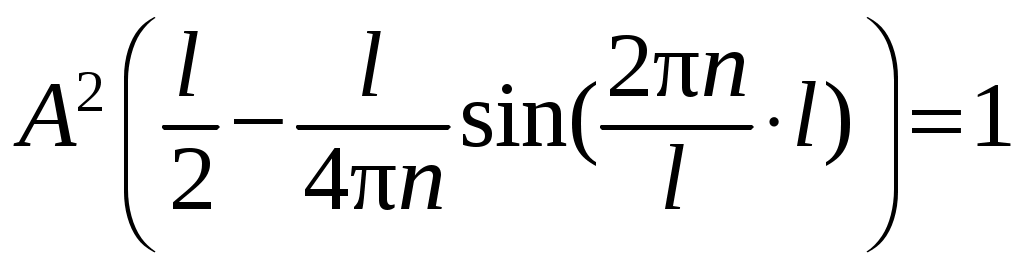 ;
; 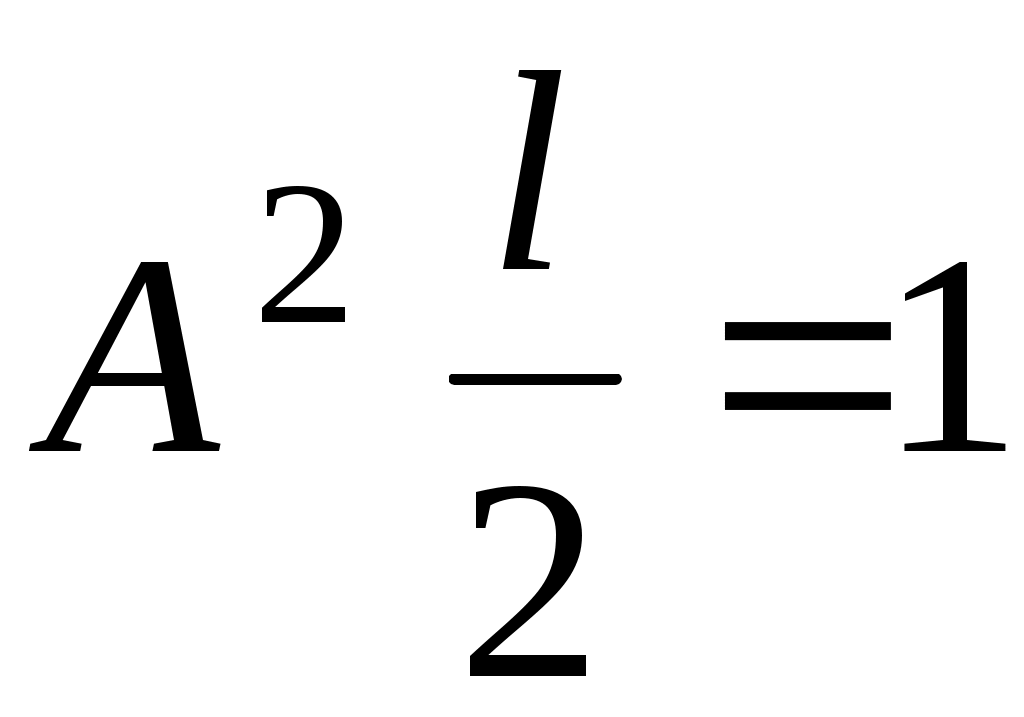
;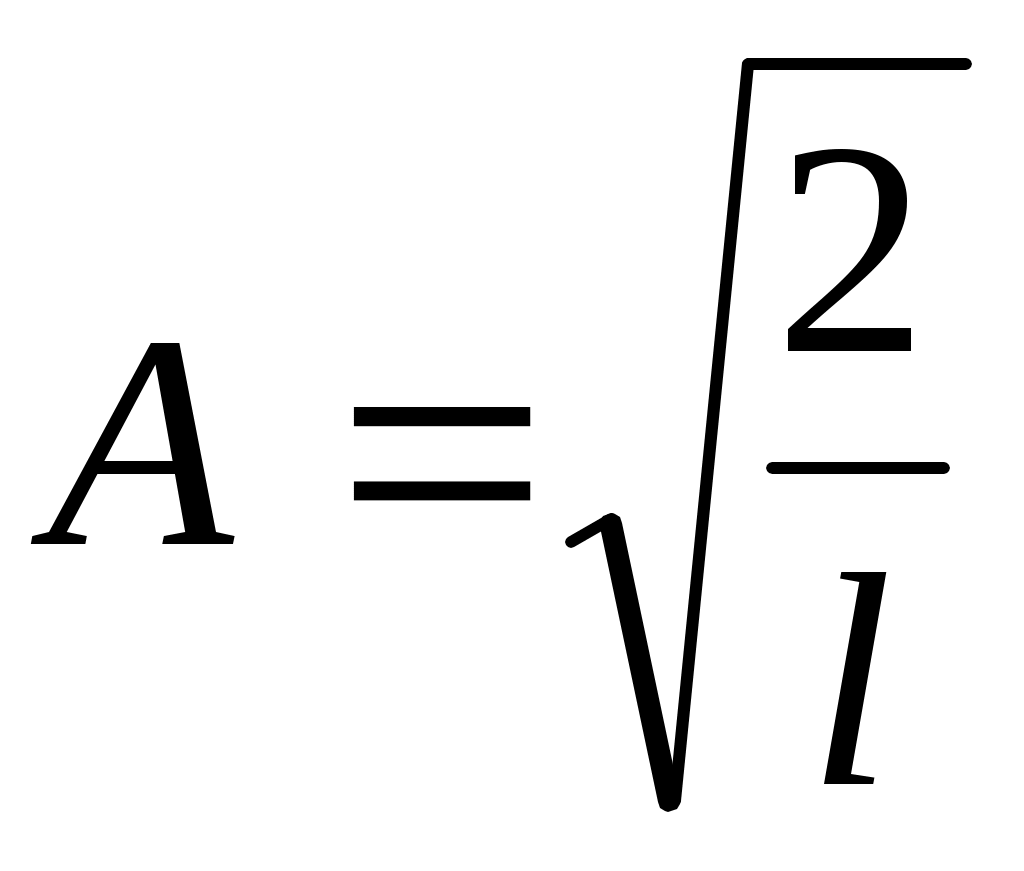 .
.
Ответ.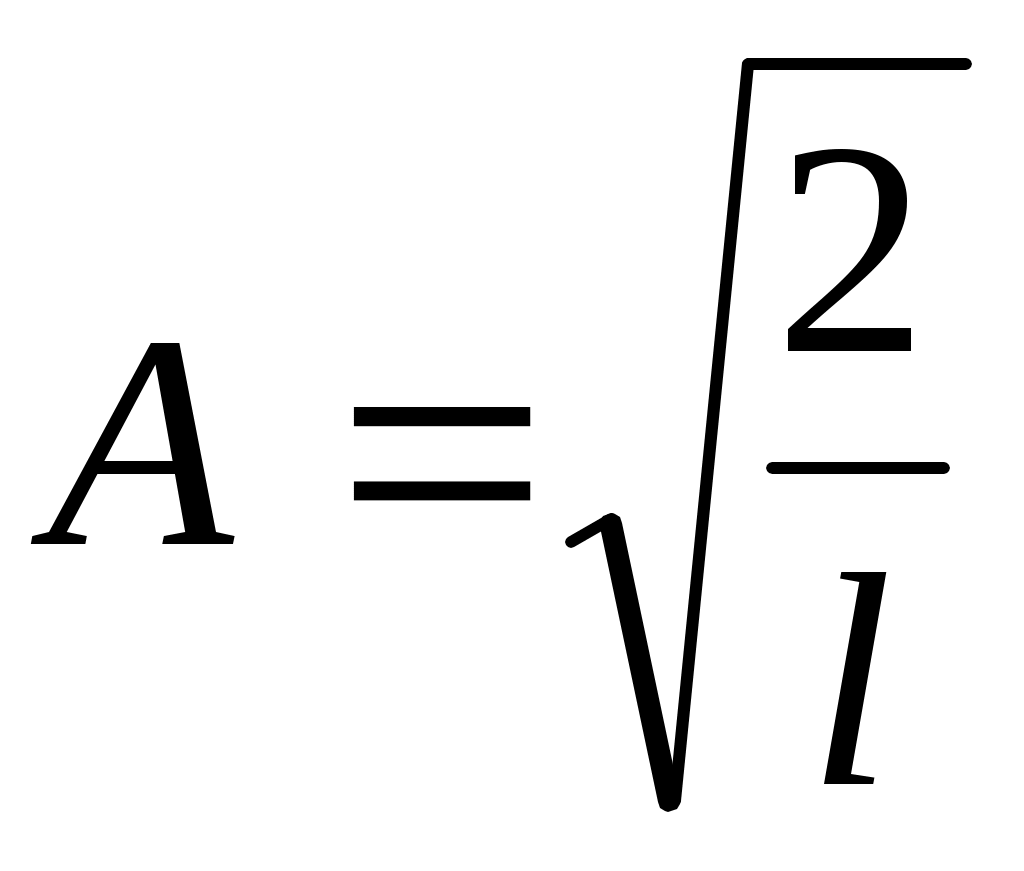 .
.
Тема 4. ТЕПЛОВЫЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
Молекулы, из которых состоят твердые тела, сильно связаны друг с другом и занимают положения, соответствующие минимуму энергии их взаимодействия. Основной формой движения этих частиц являются колебания около положения равновесия. Амплитуда колебаний составляет незначительную часть расстояния между молекулами ( 0,05 ).
Согласно классическим представлениям кристалл, состоящий из N атомов или молекул, которые рассматриваются как материальные точки, является системой с 3N колебательными степенями свободы. На каждую из них приходится в среднем энергия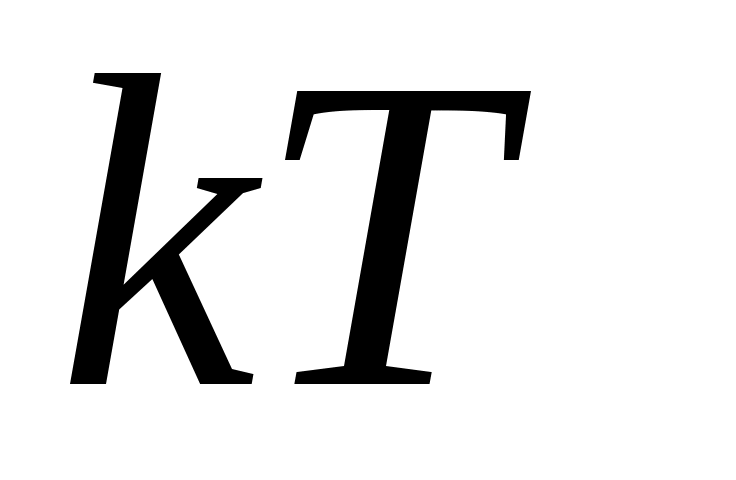 (
(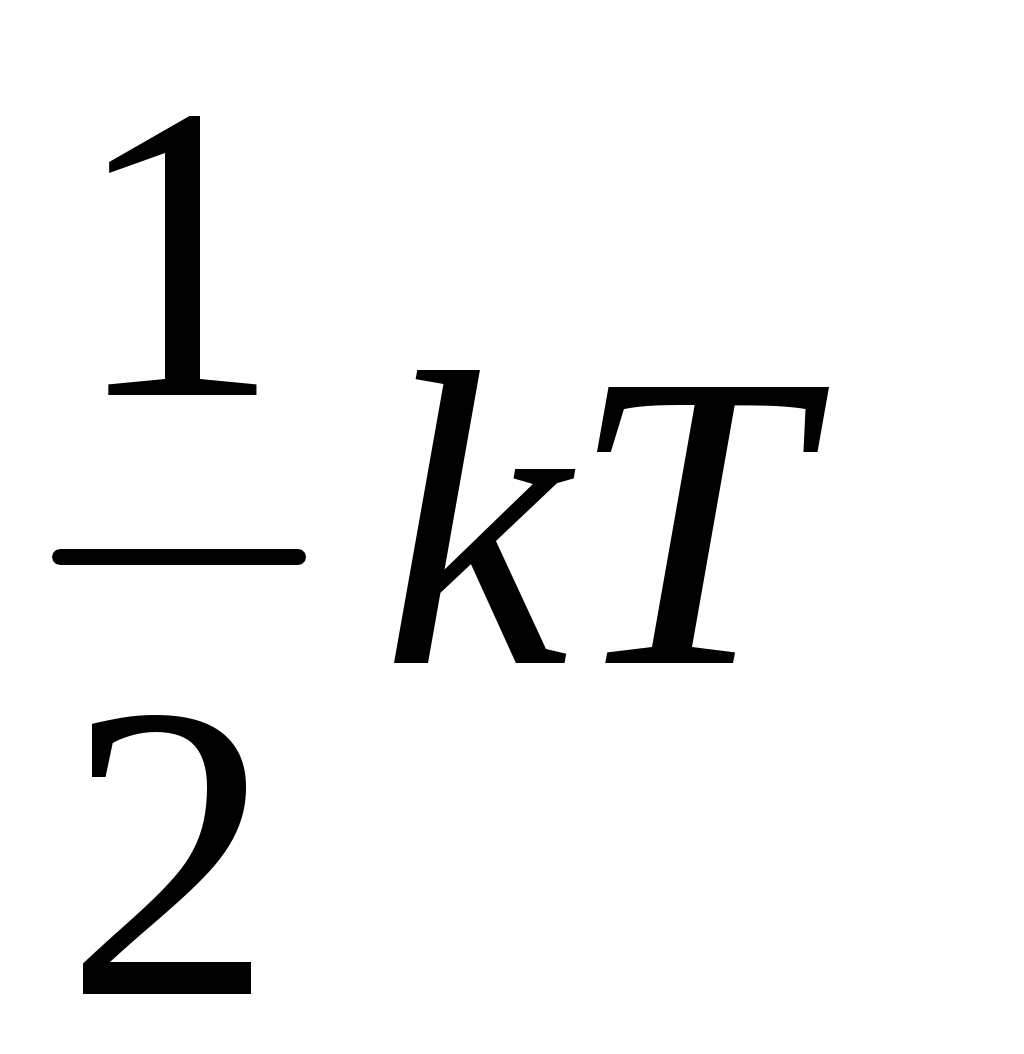 в виде кинетической и
в виде кинетической и 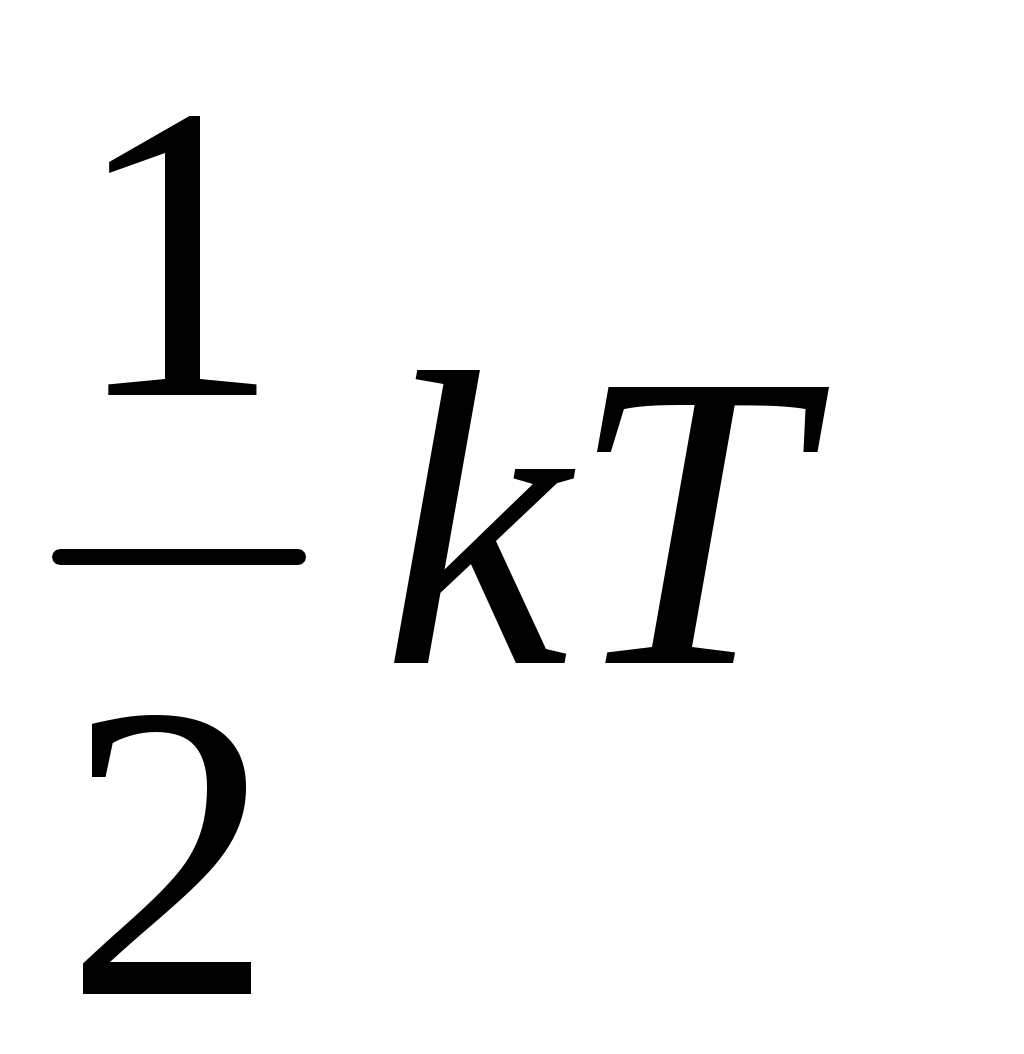 в виде потенциальной энергии), где
в виде потенциальной энергии), где  – постоянная Больцмана,
– постоянная Больцмана, 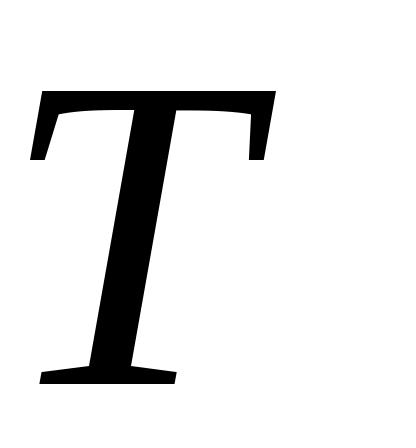 – абсолютная температура. Из этих представлений вытекает закон Дюлонга – Пти, который утверждает, что молярная теплоемкость всех кристаллов одинакова и равна
– абсолютная температура. Из этих представлений вытекает закон Дюлонга – Пти, который утверждает, что молярная теплоемкость всех кристаллов одинакова и равна 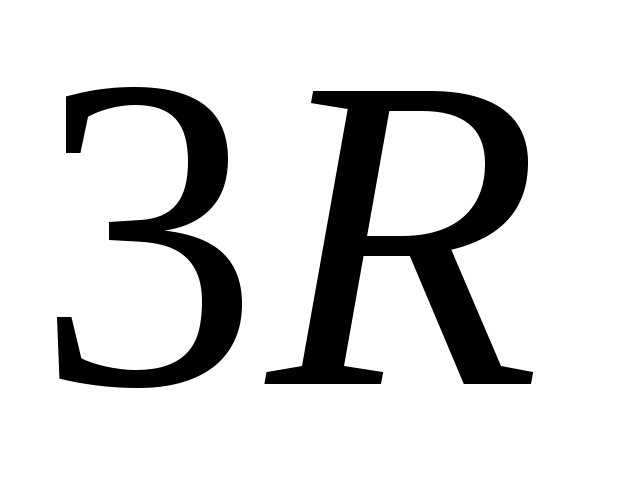 , где
, где 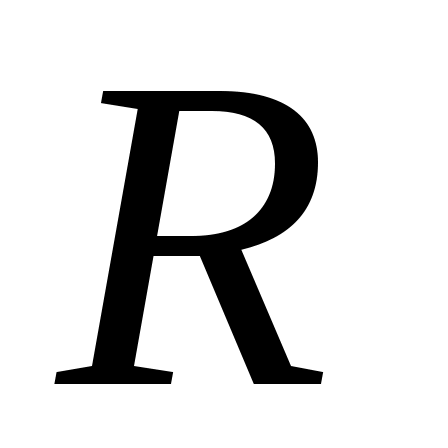 – универсальная газовая постоянная. Этот закон, как показывает опыт, хорошо выполняется для многих химически простых тел в кристаллическом состоянии при высоких температурах. При понижении температуры теплоемкость убывает, стремясь к нулю при приближении абсолютной температуры кристалла к 0К. При этом вблизи нуля теплоемкость изменяется пропорционально
– универсальная газовая постоянная. Этот закон, как показывает опыт, хорошо выполняется для многих химически простых тел в кристаллическом состоянии при высоких температурах. При понижении температуры теплоемкость убывает, стремясь к нулю при приближении абсолютной температуры кристалла к 0К. При этом вблизи нуля теплоемкость изменяется пропорционально 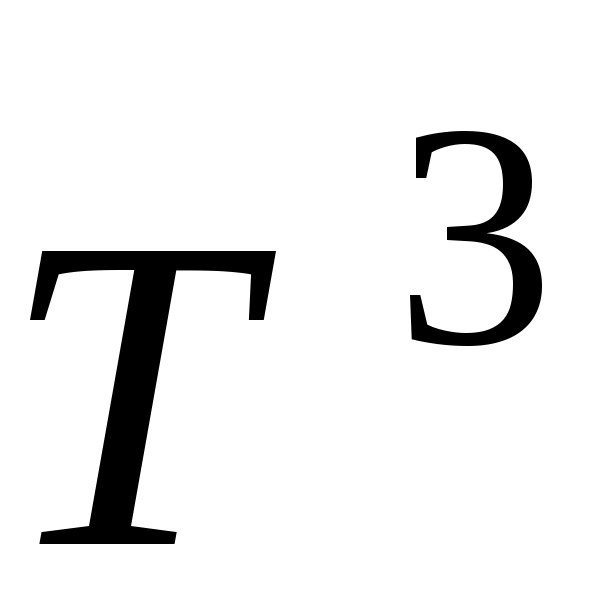 .
.
С точки зрения квантовой механики атомы химически простого твердого тела при колебаниях с малой амплитудой являются гармоническими квантовыми осцилляторами. Энергия такого осциллятора может принимать только дискретный набор значений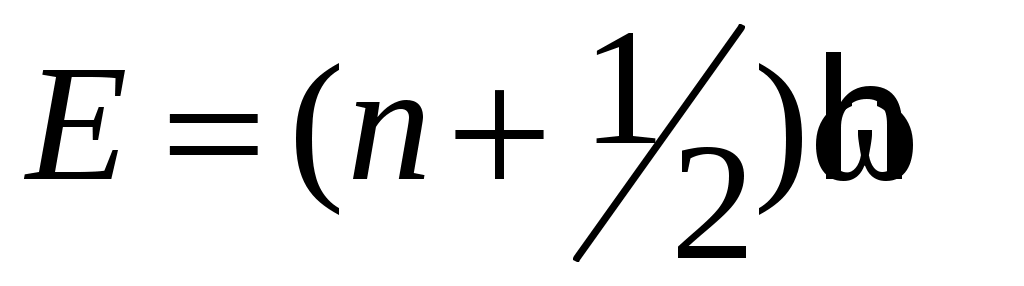
, где квантовое число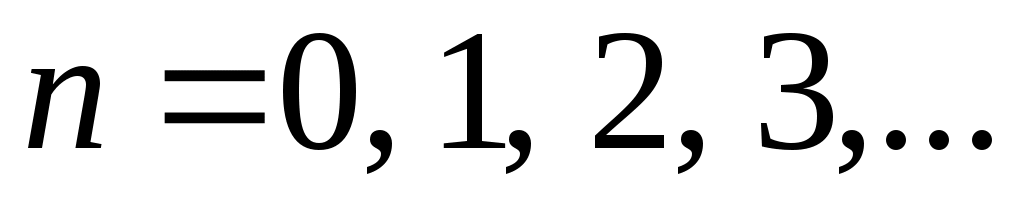 , причем изменение квантового числа
, причем изменение квантового числа  на единицу приводит к изменению энергии осциллятора на одинаковую величину, равную
на единицу приводит к изменению энергии осциллятора на одинаковую величину, равную 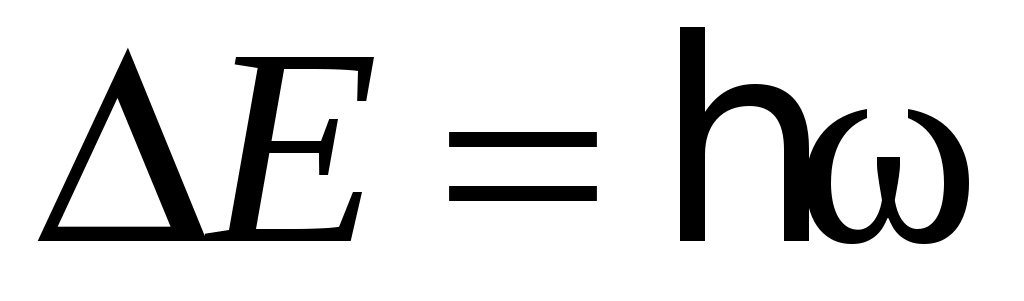 . Величина
. Величина  соответствует наименьшей, так называемой нулевой энергии колебаний
соответствует наименьшей, так называемой нулевой энергии колебаний 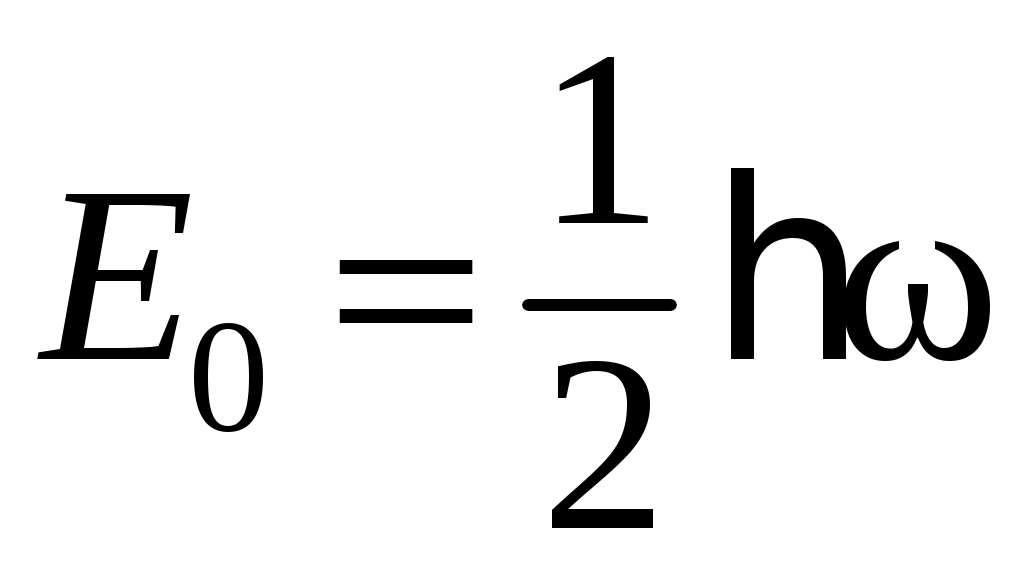 .
.
Теория теплоемкости кристаллических тел, учитывающая квантование колебательной энергии, была создана Эйнштейном и впоследствии усовершенствована Дебаем. Теория Эйнштейна дает лишь качественно верный ход зависимости теплоемкости от температуры вблизи 0К. Теория Дебая дает количественное соответствие опытным данным.
В отличие от Эйнштейна Дебай учел, что колебания атомов кристалла не являются независимыми. Смещение одного атома от положения равновесия приводит к смещению соседних с ним атомов. В результате в кристалле возникает бегущая волна. Дойдя до границ, волна отражается и начинает распространяться навстречу падающей волне. При сложении этих волн образуются стоячие волны. Из теории стоячих волн известно, что длина бегущих волн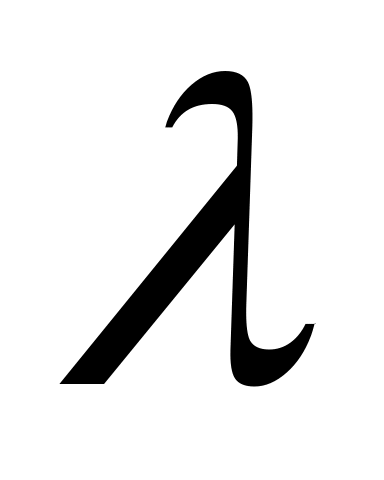 , за счет сложения которых образуются стоячие волны, может иметь только дискретный набор значений, которые связаны с размерами кристалла
, за счет сложения которых образуются стоячие волны, может иметь только дискретный набор значений, которые связаны с размерами кристалла 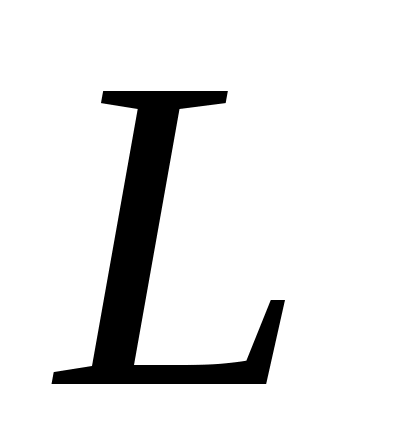 в направлении распространения волны формулой
в направлении распространения волны формулой
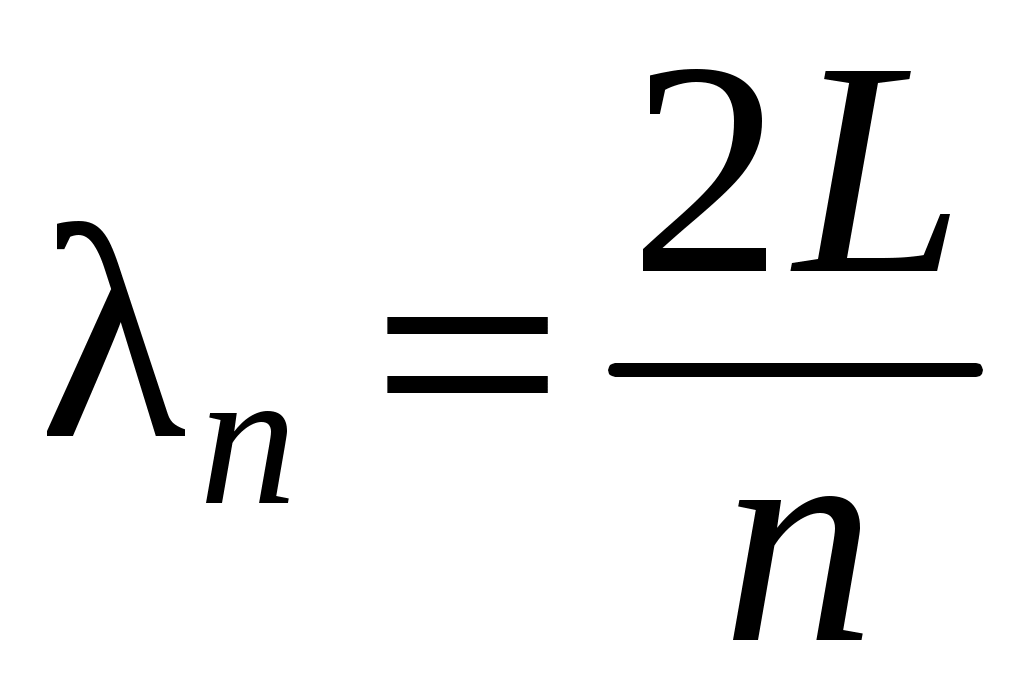 ,
,
где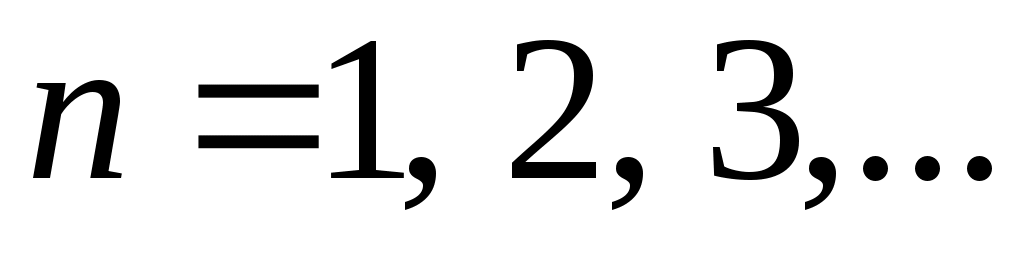 – номер гармоники.
– номер гармоники.
Каждая стоячая волна, с точки зрения квантовой механики, представляет собой квантовый гармонический осциллятор и обычно называется модой. Энергия моды с частотой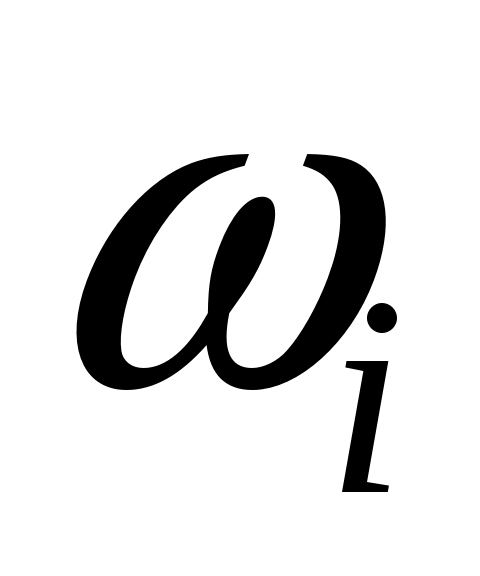 складывается из порций, равных
складывается из порций, равных 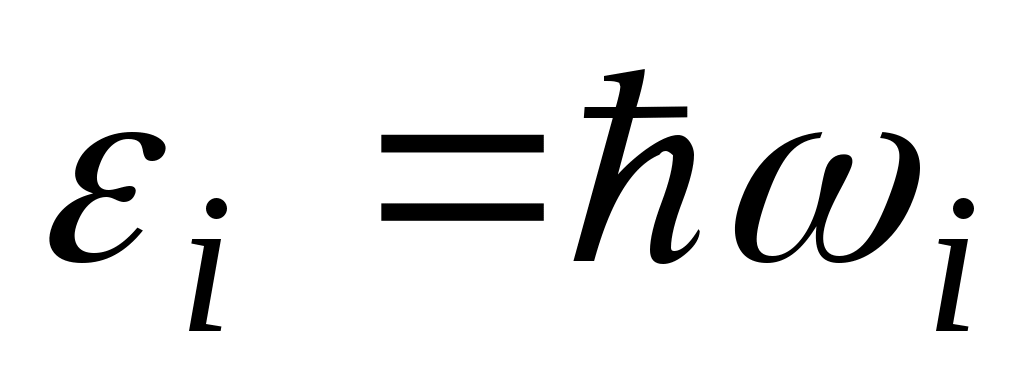 . Эта порция (квант) энергии упругих колебаний среды называется фононом
. Эта порция (квант) энергии упругих колебаний среды называется фононом
. Важно отметить, что в среде, состоящей из дискретных атомов, расположенных на расстоянии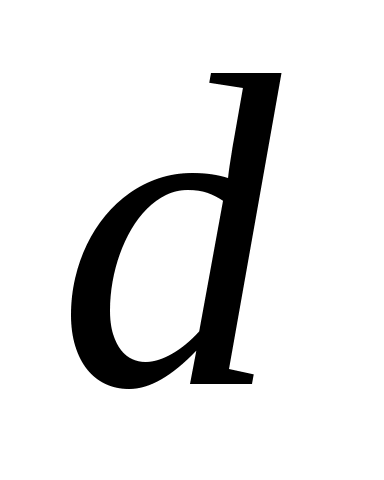 , длина волны не может быть меньше чем
, длина волны не может быть меньше чем 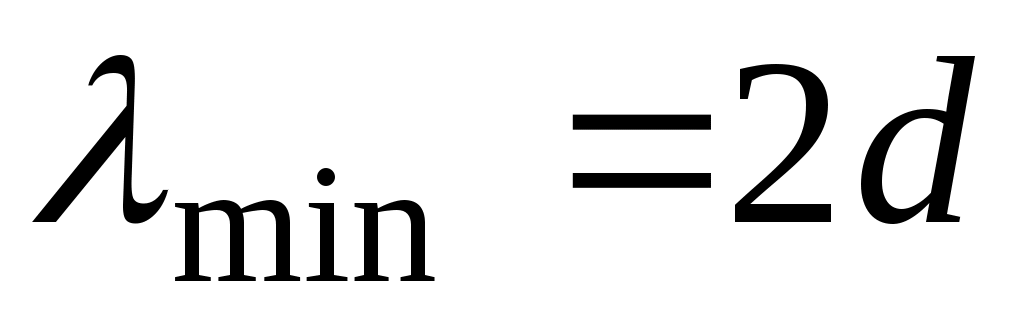 . Это означает, что циклическая частота упругих звуковых колебаний, возбуждаемых при распространении волн по кристаллу, не может быть больше чем
. Это означает, что циклическая частота упругих звуковых колебаний, возбуждаемых при распространении волн по кристаллу, не может быть больше чем
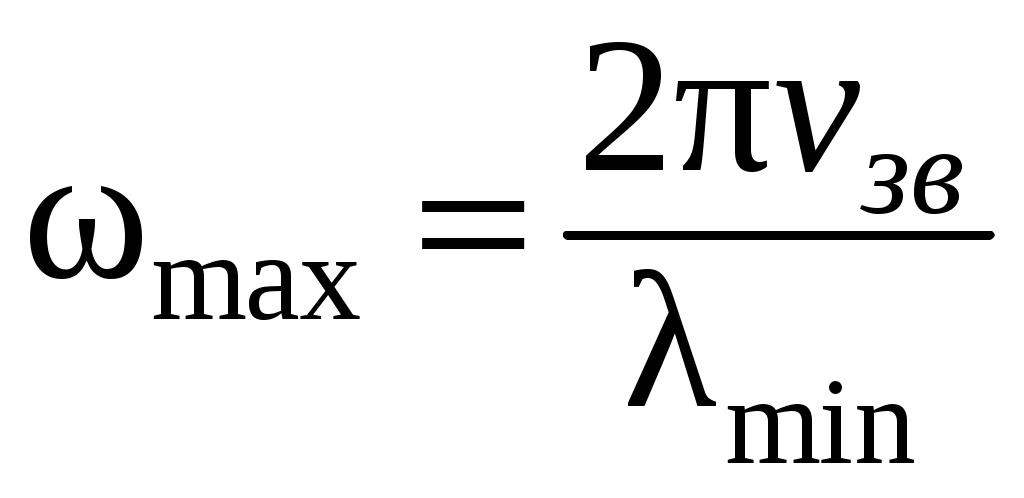 , (4.1)
, (4.1)
где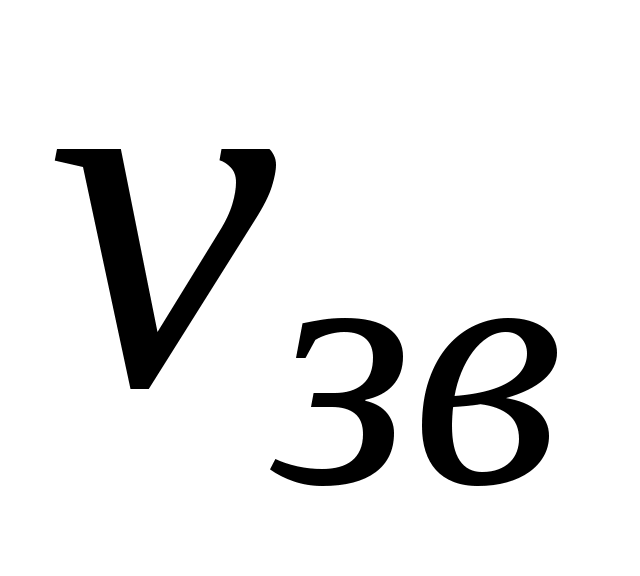 – скорость звуковых волн в кристалле (в теории Дебая
– скорость звуковых волн в кристалле (в теории Дебая 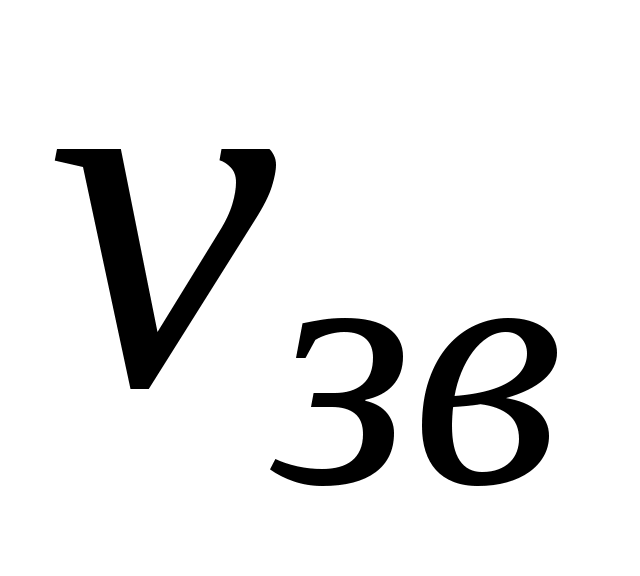 считается одинаковой для всех длин волн).
считается одинаковой для всех длин волн).
В упругой среде вдоль некоторого направления могут одновременно распространяться три разные независимые волны с одинаковыми циклическими частотами . Эти волны отличаются поляризацией: одна - продольная и две поперечные волны, поляризованные во взаимно перпендикулярных направлениях. Учитывая это, можно найти число различных мод, приходящихся на единицу объема кристалла, частоты которых лежат в диапазоне от
. Эти волны отличаются поляризацией: одна - продольная и две поперечные волны, поляризованные во взаимно перпендикулярных направлениях. Учитывая это, можно найти число различных мод, приходящихся на единицу объема кристалла, частоты которых лежат в диапазоне от  до
до 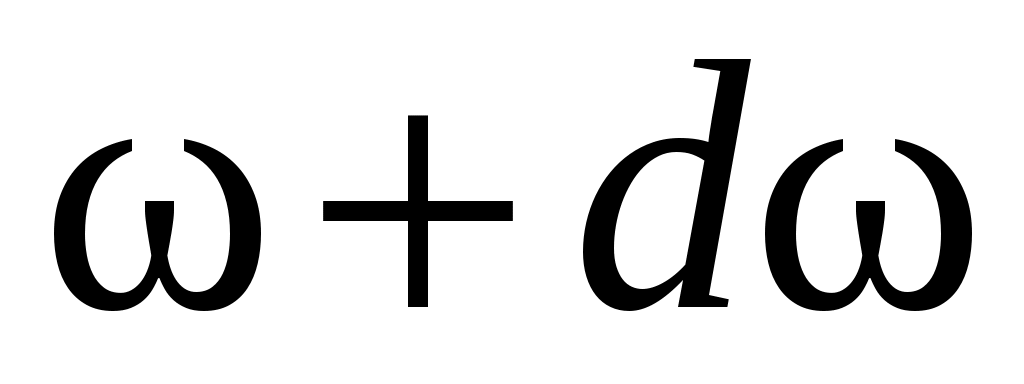 :
:
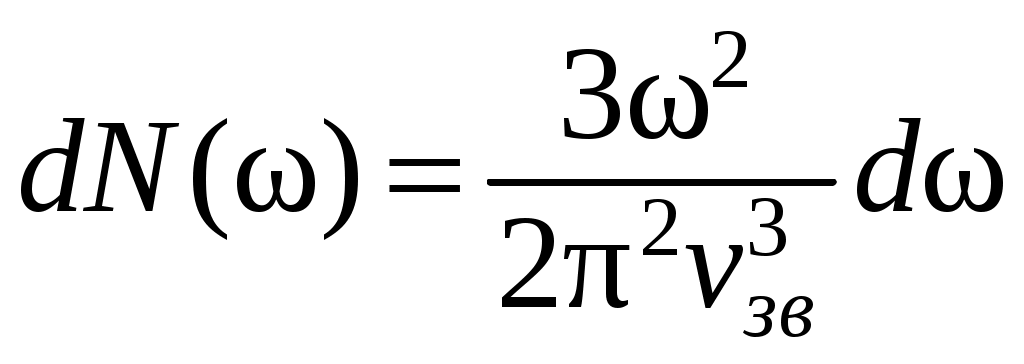 .
.
Максимальную частоту колебаний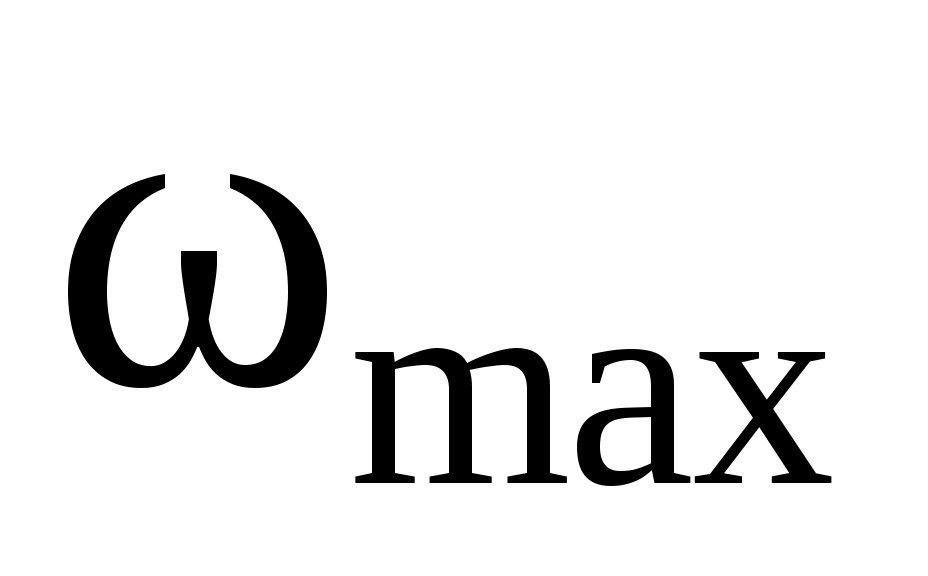 находят, приравнивая полное число фононов к числу степеней свободы
находят, приравнивая полное число фононов к числу степеней свободы 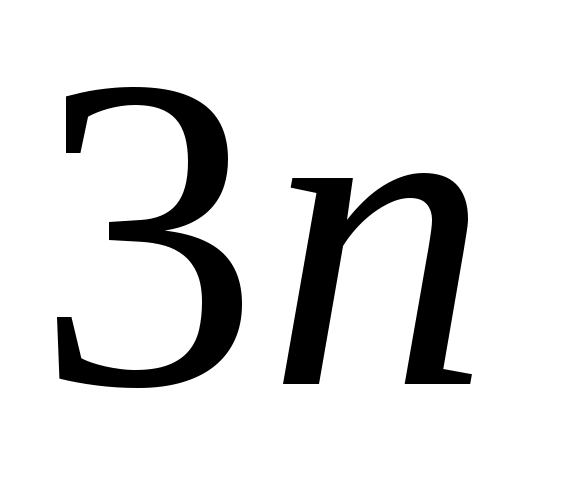 в единице объема (
в единице объема ( – число атомов в единице объема):
– число атомов в единице объема):
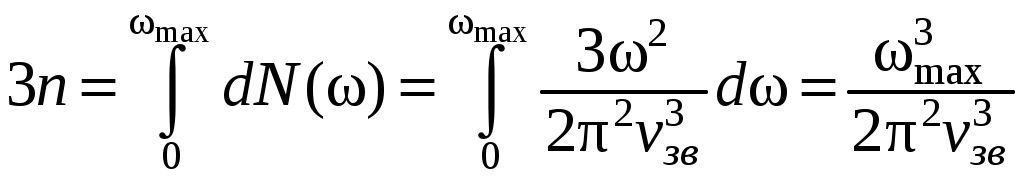 .
.
Отсюда
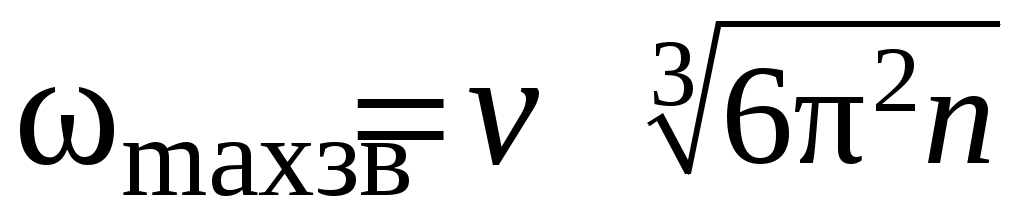 . (4.2)
. (4.2)
Используя формулу (4.2), можно получить
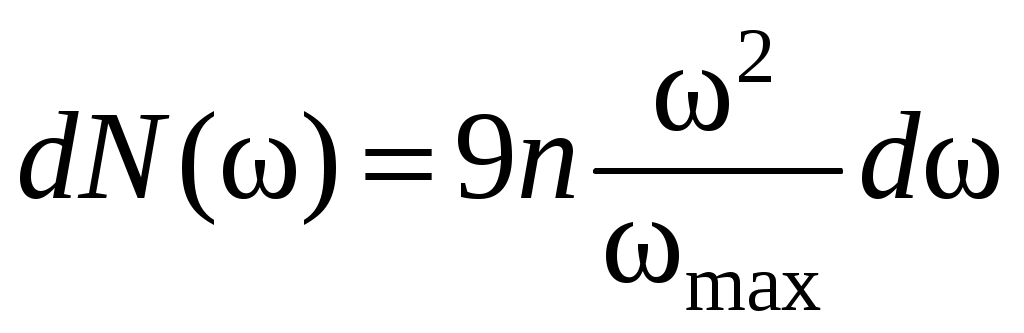 .
.
Теперь можно вычислить внутреннюю энергию тепловых колебаний единицы объема кристалла
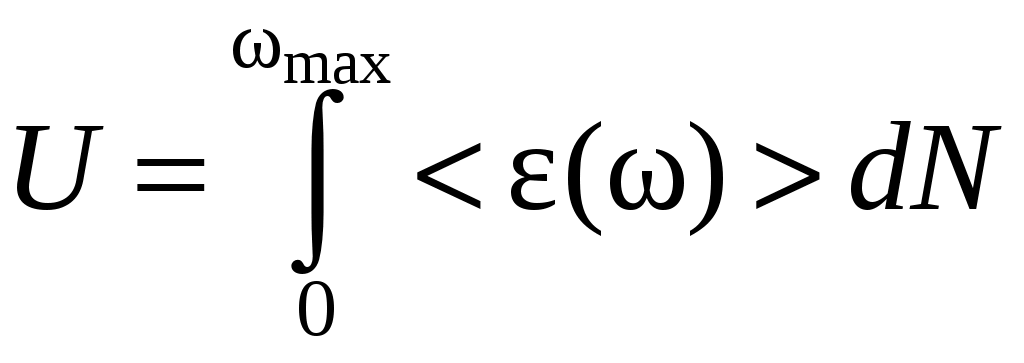
,
где средняя энергия колебаний квантового осциллятора (моды)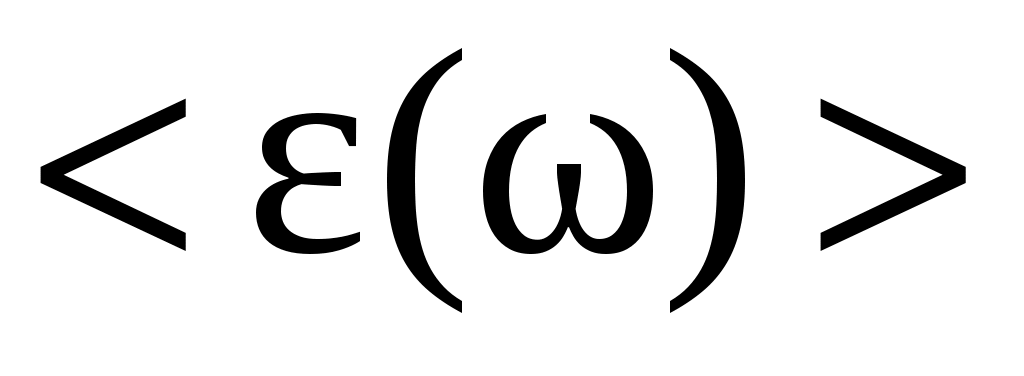 , без учета нулевой энергии колебаний, как доказывается статистической физикой, равна
, без учета нулевой энергии колебаний, как доказывается статистической физикой, равна
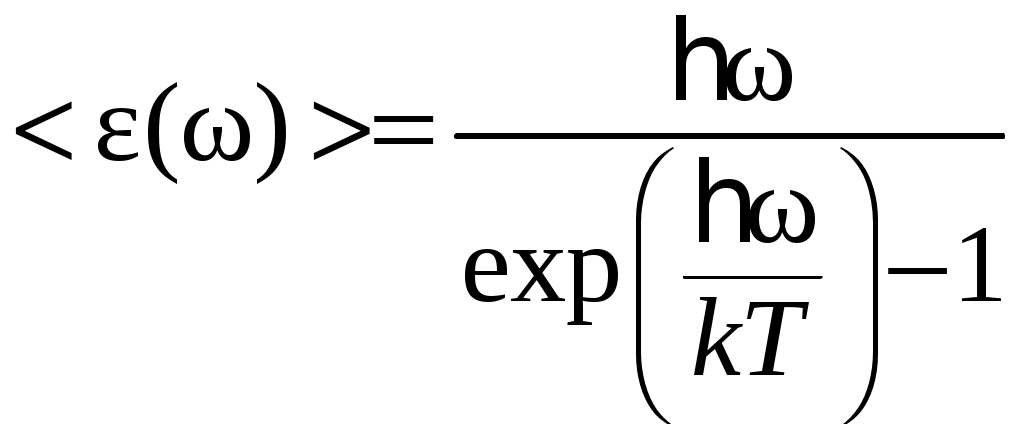 ,
,
где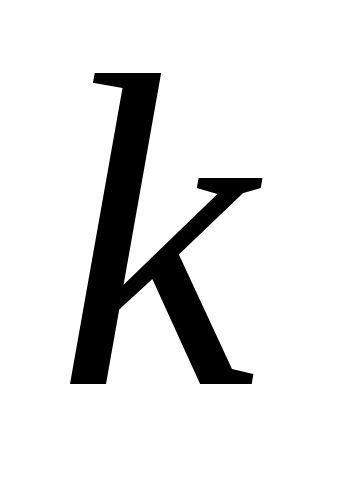 – постоянная Больцмана.
– постоянная Больцмана.
Тогда удельная теплоемкость кристалла при постоянном объеме получается
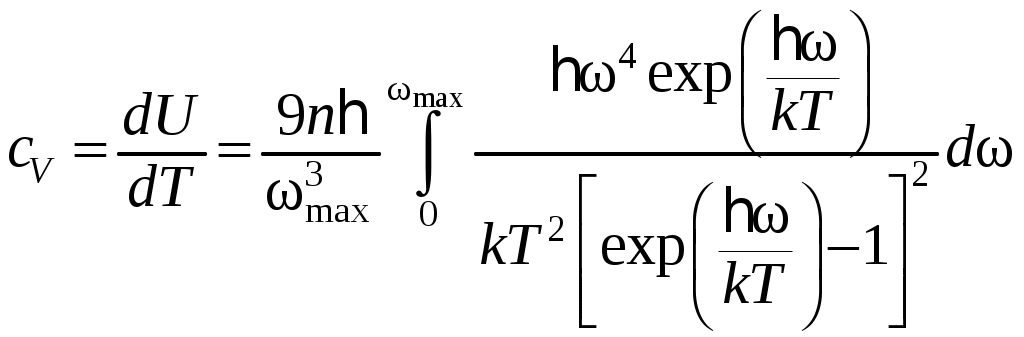 .
.
Введем характеристическую температуру Дебая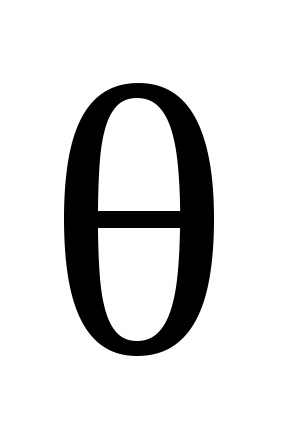 :
:
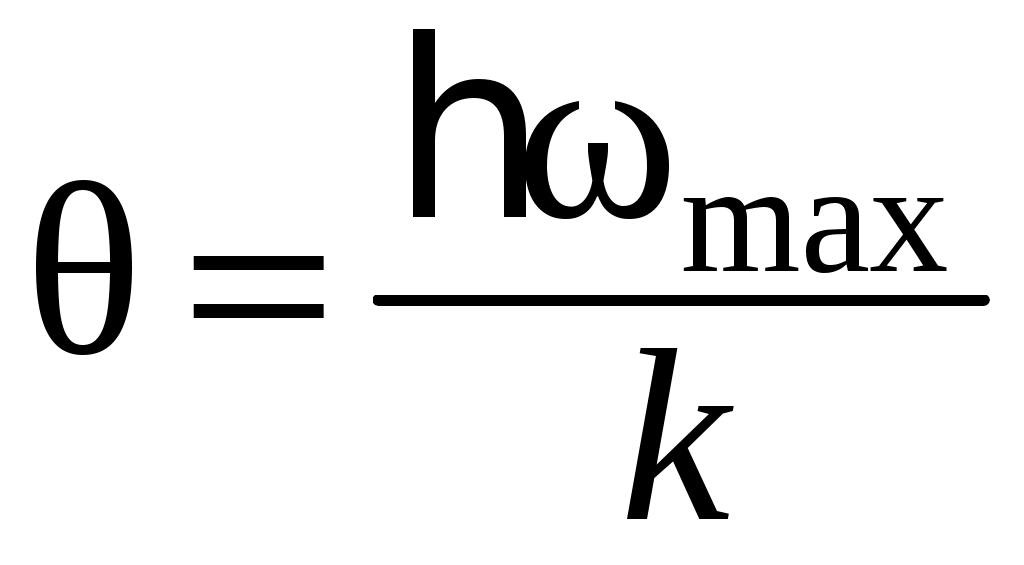 . (4.3)
. (4.3)
Кроме того, введем переменную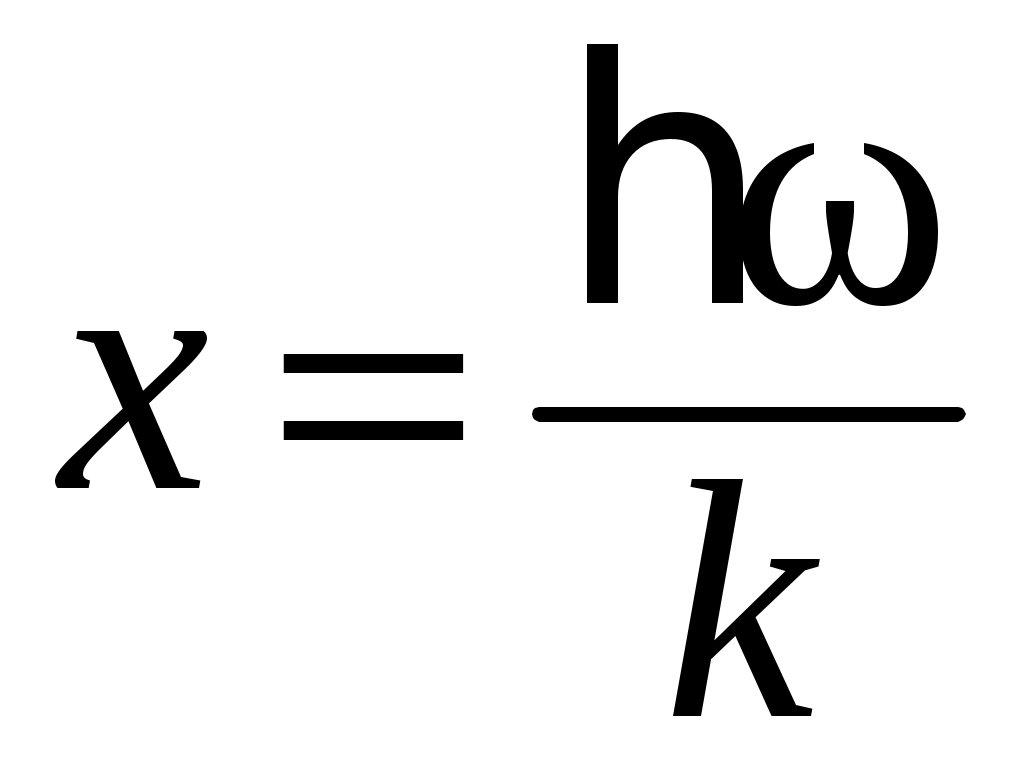 .
.
Тогда формула для удельной теплоемкости примет вид
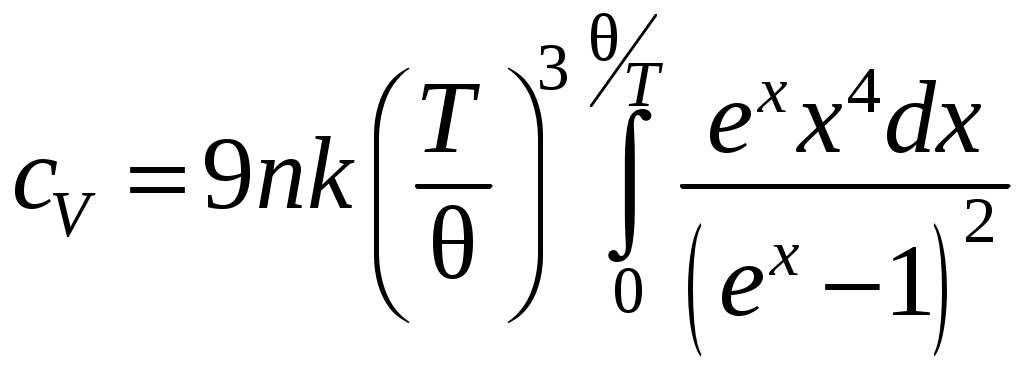 .
.
При (область низких температур) верхний предел в последнем интеграле можно заменить на
(область низких температур) верхний предел в последнем интеграле можно заменить на 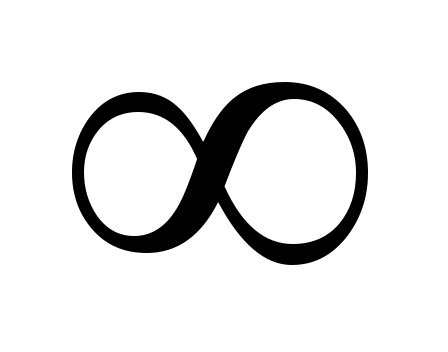 . Если, кроме того, учесть, что между удельной и молярной теплоемкостью существует связь
. Если, кроме того, учесть, что между удельной и молярной теплоемкостью существует связь
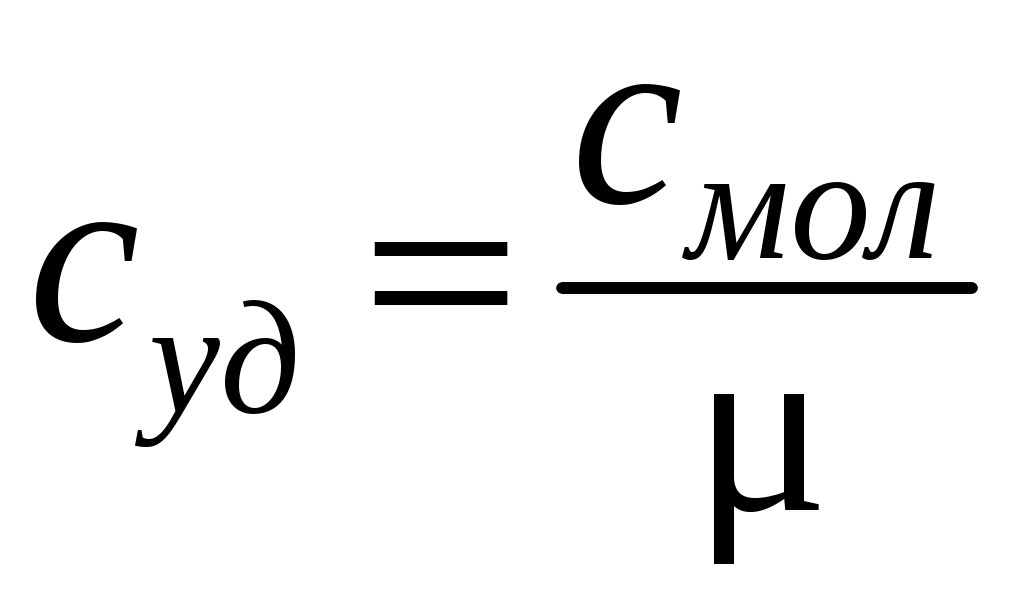 ,
,
где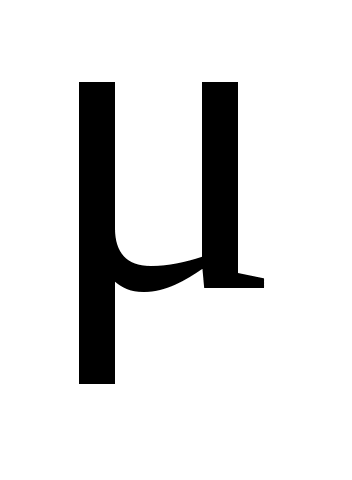 – молярная масса, то для молярной теплоемкости кристалла при постоянном объеме можно получить
– молярная масса, то для молярной теплоемкости кристалла при постоянном объеме можно получить
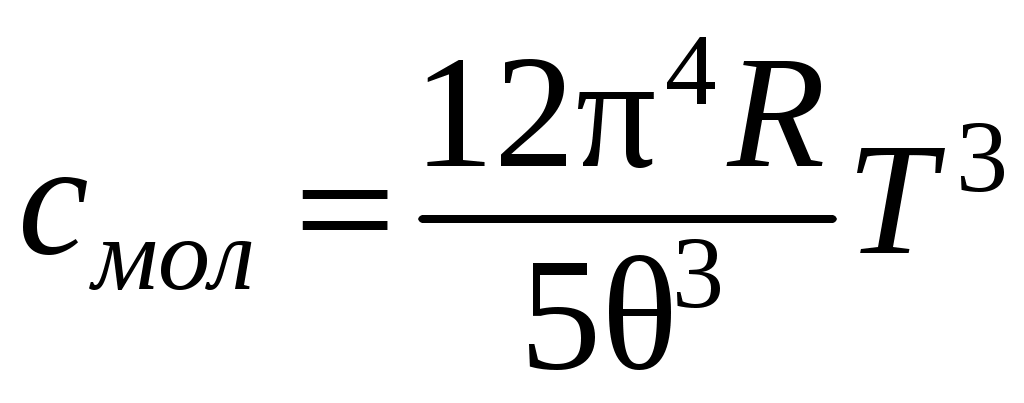 .
.
Для высоких температур , раскладывая экспоненту в ряд по малому параметру
, раскладывая экспоненту в ряд по малому параметру 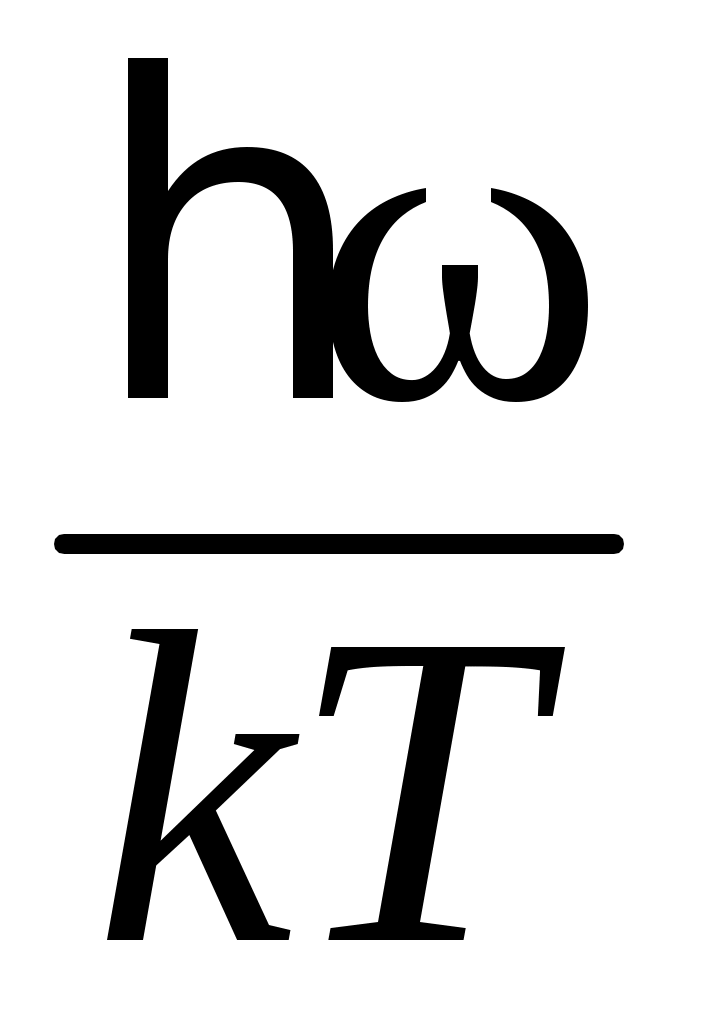 и ограничиваясь двумя членами ряда, для молярной теплоемкости получим закон Дюлонга-Пти:
и ограничиваясь двумя членами ряда, для молярной теплоемкости получим закон Дюлонга-Пти:
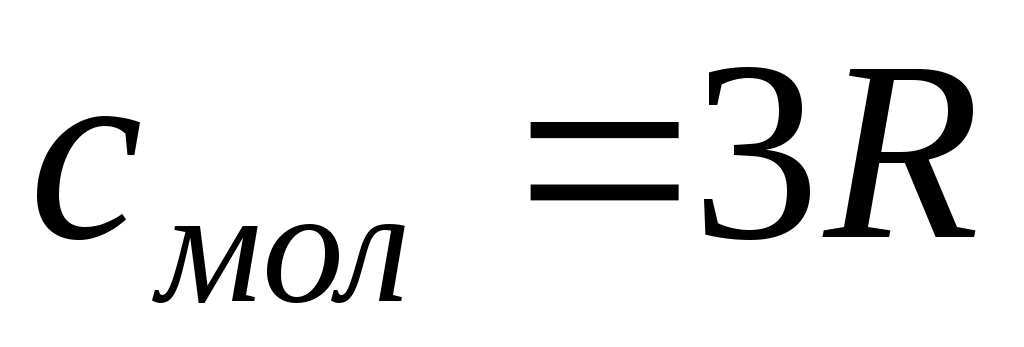 .
.
Задача. Определите приближенно скорость звука в алмазе, зная, что дебаевская температура алмаза равна 1860К и расстояние между атомами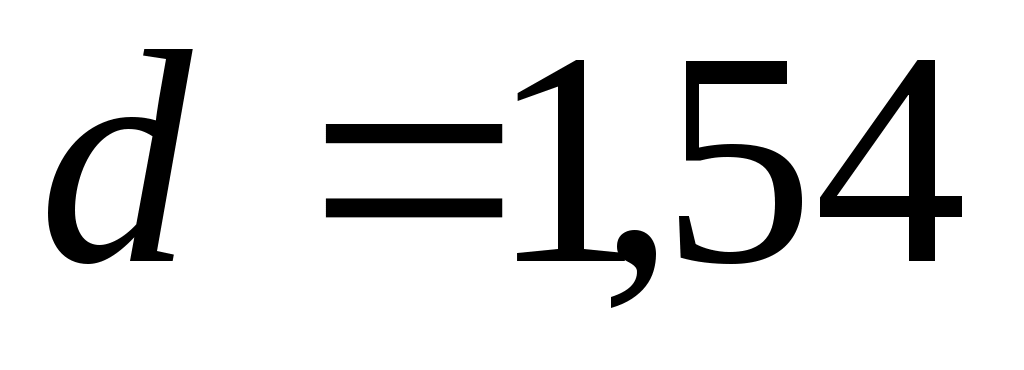
Таким образом, при движении частицы-волны в ограниченной области пространства уравнение Шредингера имеет решение лишь для определенных (квантовых) значений полной энергии. Они называются собственными значениями, а соответствующие им –функции – собственными функциями:
Вероятность и плотность вероятности обнаружить частицу в бесконечно малой области одномерного пространства
Г

Рис 3.2. Плотность веро-ятности нахождения
частицы в яме
рафики зависимости плотности вероятности от координаты для различных значений квантового числа
Задача. Собственные функции, описывающие состояние частицы, находящейся в одномерной бесконечно глубокой потенциальной яме, имеют вид
Рис. 3.2.
Плотность вероятности нахождения частицы в яме
Решение. Поскольку частица, согласно условию задачи, находится в некотором месте пространства, то вероятность обнаружить ее в диапазоне значений координаты
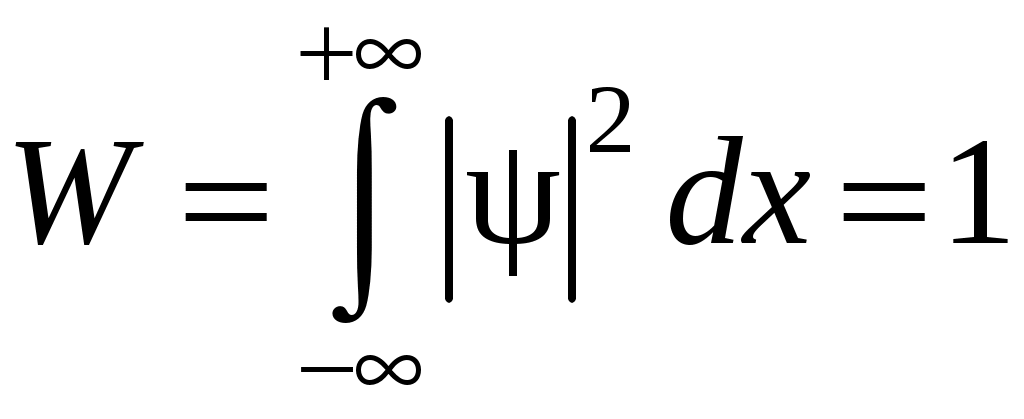 .
.Область интегрирования можно ограничить диапазоном
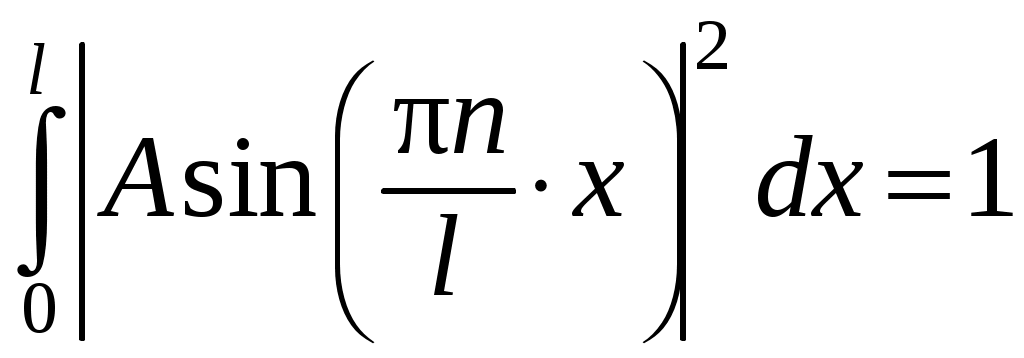 ,
, 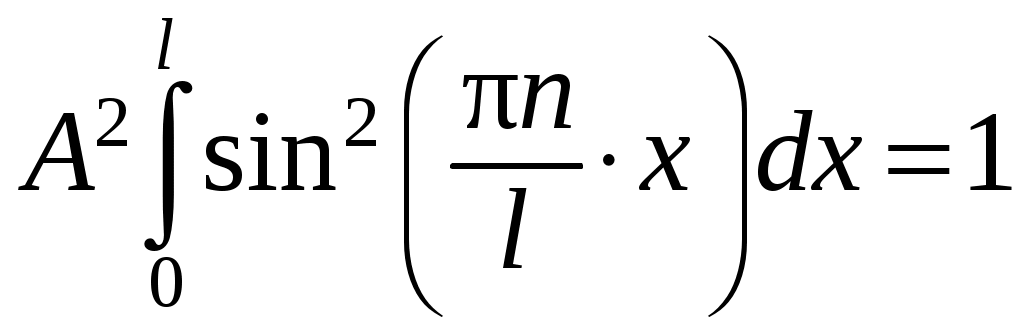 .
.Отсюда следует
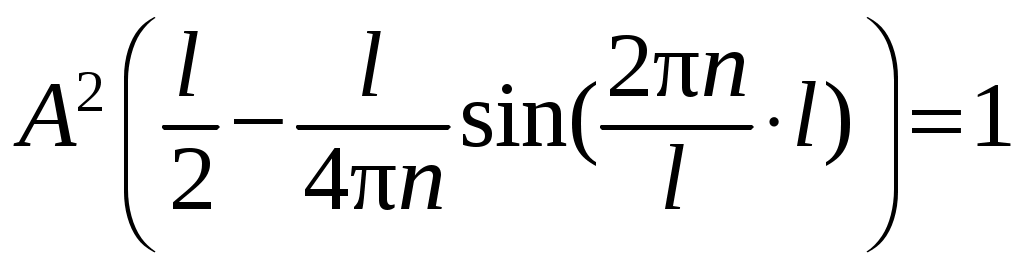 ;
; ;
Ответ.
Тема 4. ТЕПЛОВЫЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
Молекулы, из которых состоят твердые тела, сильно связаны друг с другом и занимают положения, соответствующие минимуму энергии их взаимодействия. Основной формой движения этих частиц являются колебания около положения равновесия. Амплитуда колебаний составляет незначительную часть расстояния между молекулами ( 0,05 ).
Согласно классическим представлениям кристалл, состоящий из N атомов или молекул, которые рассматриваются как материальные точки, является системой с 3N колебательными степенями свободы. На каждую из них приходится в среднем энергия
С точки зрения квантовой механики атомы химически простого твердого тела при колебаниях с малой амплитудой являются гармоническими квантовыми осцилляторами. Энергия такого осциллятора может принимать только дискретный набор значений
, где квантовое число
Теория теплоемкости кристаллических тел, учитывающая квантование колебательной энергии, была создана Эйнштейном и впоследствии усовершенствована Дебаем. Теория Эйнштейна дает лишь качественно верный ход зависимости теплоемкости от температуры вблизи 0К. Теория Дебая дает количественное соответствие опытным данным.
В отличие от Эйнштейна Дебай учел, что колебания атомов кристалла не являются независимыми. Смещение одного атома от положения равновесия приводит к смещению соседних с ним атомов. В результате в кристалле возникает бегущая волна. Дойдя до границ, волна отражается и начинает распространяться навстречу падающей волне. При сложении этих волн образуются стоячие волны. Из теории стоячих волн известно, что длина бегущих волн
где
Каждая стоячая волна, с точки зрения квантовой механики, представляет собой квантовый гармонический осциллятор и обычно называется модой. Энергия моды с частотой
. Важно отметить, что в среде, состоящей из дискретных атомов, расположенных на расстоянии
где
В упругой среде вдоль некоторого направления могут одновременно распространяться три разные независимые волны с одинаковыми циклическими частотами
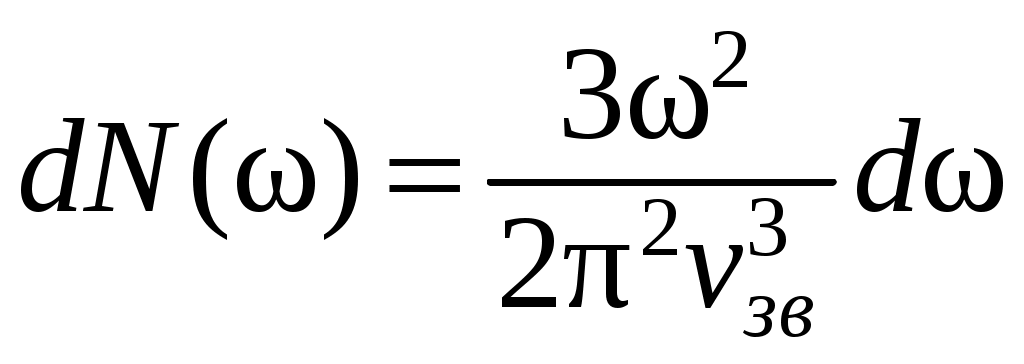 .
.Максимальную частоту колебаний
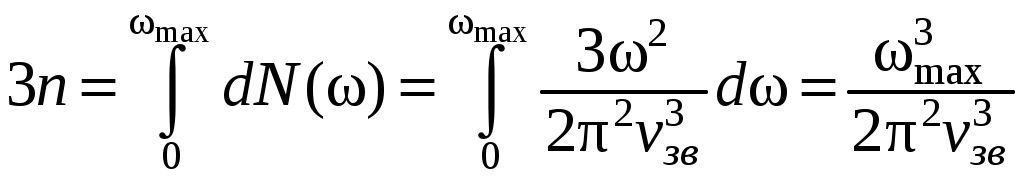 .
.Отсюда
Используя формулу (4.2), можно получить
Теперь можно вычислить внутреннюю энергию тепловых колебаний единицы объема кристалла
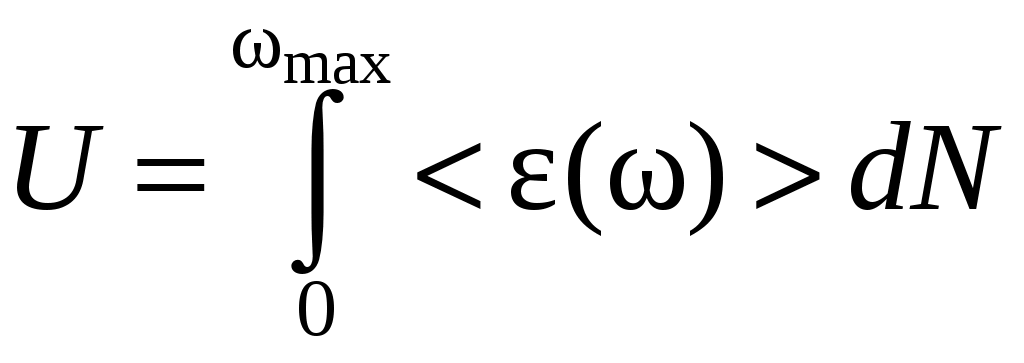
,
где средняя энергия колебаний квантового осциллятора (моды)
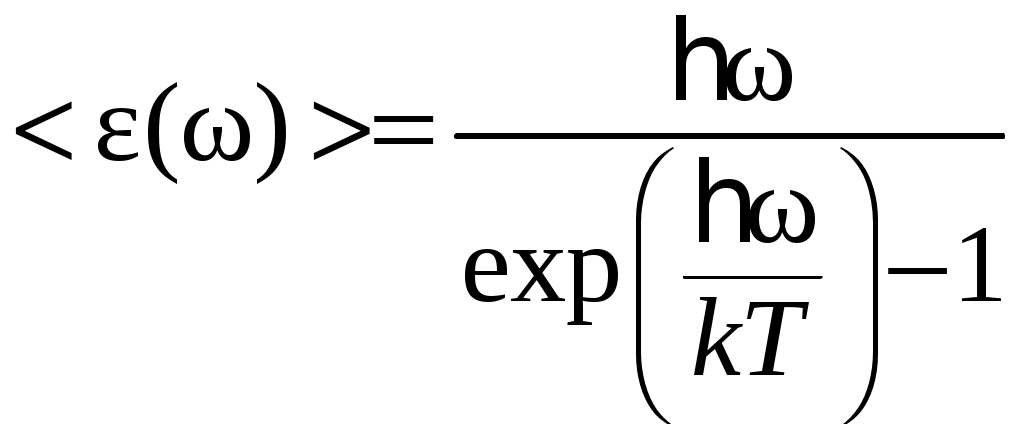 ,
,где
Тогда удельная теплоемкость кристалла при постоянном объеме получается
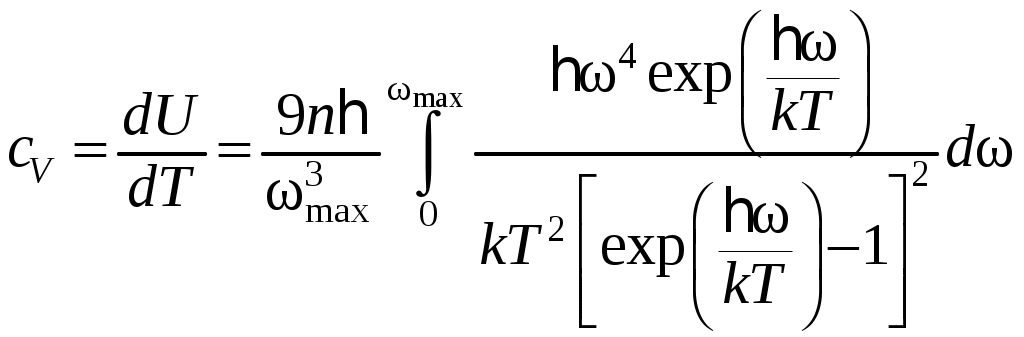 .
.Введем характеристическую температуру Дебая
Кроме того, введем переменную
Тогда формула для удельной теплоемкости примет вид
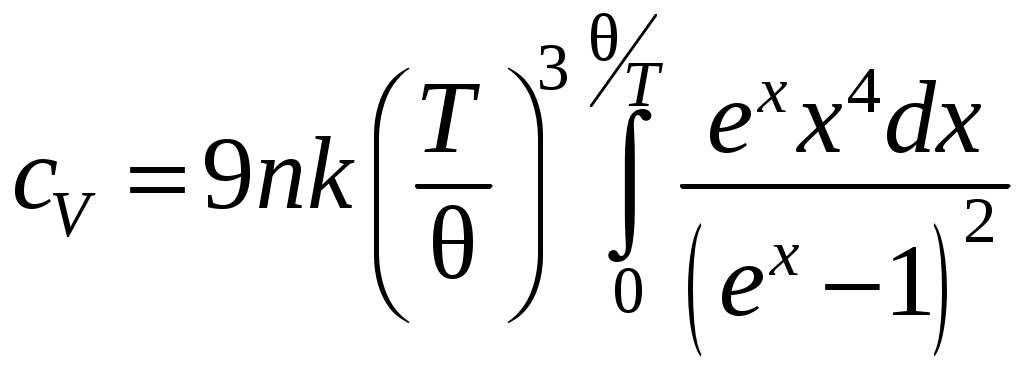 .
.При
где
Для высоких температур
Задача. Определите приближенно скорость звука в алмазе, зная, что дебаевская температура алмаза равна 1860К и расстояние между атомами