ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 615
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Линейный и множественный коэффициенты корреляции. Сущность и экономическая интерпретация.
Коэффициент корреляции - это мера линейной зависимости двух случайных величин в теории вероятностей и статистике. Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором - также и её направление.

Случайная величина в теории вероятности
Коэффициент корреляции - это статистический показатель, показывающий, насколько связаны между собой колебания значений двух других показателей. Например, насколько движение доходности ПИФа связано, перекликается (коррелирует) с движением индекса, выбранного для расчета коэффициента бета для этого ПИФа. Чем ближе значение коэффициента корреляции к 1, тем больше коррелируют ПИФ и индекс, а значит коэффициент бета и, следовательно, коэффициент альфа можно принимать к рассмотрению. Если значение этого коэффициента корреляции меньше 0,75, то указанные показатели бессмысленны.

Круговорот случайных величин
Корреляционный анализ занимается степенью связи между двумя случайными величинами Х и Y.
Корреляционный анализ экспериментальных данных для двух случайных величин заключает в себе следующие основные приемы:
1. Вычисление выборочных коэффициентов корреляции.
2. Составление корреляционной таблицы.
3. Проверка статистической гипотезы значимости связи.
ОПРЕДЕЛЕНИЕ. Корреляционная зависимость между случайными величинами Х и Y называется линейной корреляцией, если обе функции регрессии f(x) и φ(x) являются линейными. В этом случае обе линии регрессии являются прямыми; они называется прямыми регрессии.
Для достаточно полного описания особенностей корреляционной зависимости между величинами недостаточно определить форму этой зависимости и в случае линейной зависимости оценить ее силу по величине коэффициента регрессии. Например, ясно, что корреляционная зависимость возраста Y учеников средней
школы от года Х их обучения в школе является, как правило, более тесной, чем аналогичная зависимость возраста студентов высшего учебного заведения от года обучения, поскольку среди студентов одного и того же года обучения в вузе обычно наблюдается больший разброс в возраcте, чем у школьников одного и того же класса.
Для оценки тесноты линейных корреляционных зависимостей между величинами Х и Y по результатам выборочных наблюдений вводится понятие выборочного коэффициента линейной корреляции, определяемого формулой:
где σX и σY выборочные средние квадратические отклонения величин Х и Y, которые вычисляются по формулам:
Следует отметить, что основной смысл выборочного коэффициента линейной корреляции rB состоит в том, что он представляет собой эмпирическую (т.е. найденную по результатам наблюдений над величинами Х и Y) оценку соответствующего генерального коэффициента линейной корреляции r: r=rB (9)
Принимая во внимание формулы:
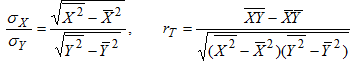
видим, что выборочное уравнение линейной регрессии Y на Х имеет вид:
где
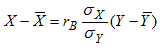 (11)
(11)Основные свойства выборочного коэффициента линейной корреляции:
1. Коэффициент корреляции двух величин, не связанных линейной корреляционной зависимостью, равен нулю.
2. Коэффициент корреляции двух величин, связанных линейной корреляционной зависимостью, равен 1 в случае возрастающей зависимости и -1 в случае убывающей зависимости.
3. Абсолютная величина коэффициента корреляции двух величин, связанных линейной корреляционной зависимостью, удовлетворяет неравенству 0<|r|<1. При этом коэффициент корреляции положителен, если корреляционная зависимость возрастающая, и отрицателен, если корреляционная зависимость убывающая.
4. Чем ближе |r| к 1, тем теснее прямолинейная корреляция между величинами Y, X.
По своему характеру корреляционная связь может быть прямой и обратной, а по силе – сильной, средней, слабой. Кроме того, связь может отсутствовать или быть полной.
Сила и характер связи между параметрами
| Сила связи | Характер связи | |
| Прямая (+) | Обратная (-) | |
| Полная | 1 | -1 |
| Сильная | От 0,7 до 1 | От -0,7 до -1 |
| Средняя | От 0,3 до 0,7 | От -0,3 до -0,7 |
| Слабая | От 0,3 до 0 | От -0,3 до 0 |
| Связь отсутсвует | 0 | 0 |
Пример 4. Изучалась зависимость между двумя величинами Y и Х. Результаты наблюдений приведены в таблице в виде двумерной выборки объема 11:
| X | 68 | 37 | 50 | 53 | 75 | 66 | 52 | 65 | 74 | 65 | 54 |
| Y | 114 | 149 | 146 | 141 | 114 | 112 | 124 | 105 | 141 | 120 | 124 |
Требуется:
1) Вычислить выборочный коэффициент корреляции;
2) Оценить характер и силу корреляционной зависимости;
3) Написать уравнение линейной регрессии Y на Х.
Решение. По известным формулам:
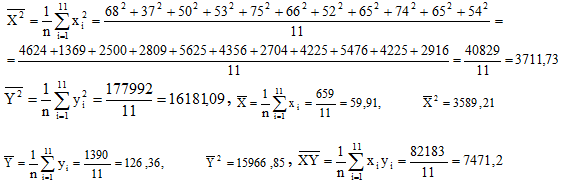
Отсюда, по (7) и (8):
Таким образом, следует сделать вывод, что рассматриваемая корреляционная зависимость между величинами Х и Y является по характеру – обратной, по силе – средней.
3) Уравнение линейной регрессии Y на Х:
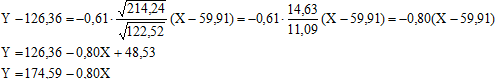
Пример 5. Изучалась зависимость между качеством Y (%) и количеством Х (шт). Результаты наблюдений приведены в виде корреляционной таблицы:
| Y\X | 18 | 22 | 26 | 30 | ny |
| 70 | 5 | | | | 5 |
| 75 | 7 | 46 | 1 | | 54 |
| 80 | | 29 | 72 | | 101 |
| 85 | | | 29 | 8 | 37 |
| 90 | | | | 3 | 3 |
| nx | 12 | 75 | 102 | 11 | 200 |
Требуется вычислить выборочный коэффициент линейной корреляции зависимости Y от Х.
Решение. Для упрощения вычислений перейдем к новым переменным – условным вариантам (ui, vi), воспользовавшись формулами (*) (§3) при h1=4, h2=5, x0=26, y0=80. Для удобства перепишем данную таблицу в новых обозначениях:
| u\v | -2 | -1 | 0 | 1 | nv |
| -2 | 5 | | | | 5 |
| -1 | 7 | 46 | 1 | | 54 |
| 0 | | 29 | 72 | | 101 |
| 1 | | | 29 | 8 | 37 |
| 2 | | | | 3 | 3 |
| nu | 12 | 75 | 102 | 11 | 200 |
Имеем при xi=ui и yj=vj:
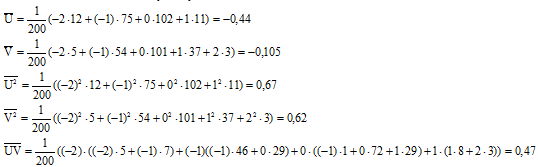
Таким образом:
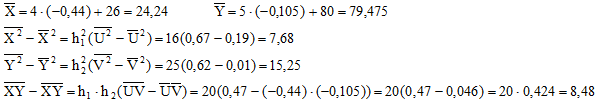
Отсюда,
Вывод: Корреляционная зависимость между величинами Х и Y - прямая и сильная.
Множественный коэффициент корреляции характеризует тесноту линейной связи между одной переменной и совокупностью других рассматриваемых переменных.
Особое значение имеет расчет множественного коэффициента корреляции результативного признака y с факторными x1, x2,…, xm, формула для определения которого в общем случае имеет вид
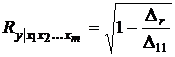
где ∆r – определитель корреляционной матрицы; ∆11 – алгебраическое дополнение элемента ryy корреляционной матрицы.
Если рассматриваются лишь два факторных признака, то для вычисления множественного коэффициента корреляции можно использовать следующую формулу:
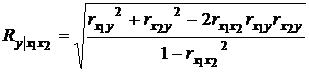
Построение множественного коэффициента корреляции целесообразно только в том случае, когда частные коэффициенты корреляции оказались значимыми, и связь между результативным признаком и факторами, включенными в модель, действительно существует.
- 1 ... 10 11 12 13 14 15 16 17 ... 21