Файл: Тема 1 Макроэкономика ее предмет и методы познания макроэкономических процессов.docx

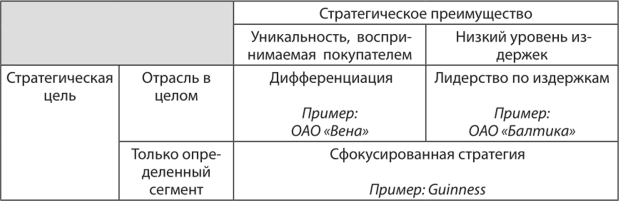
Рис. 3.3. Типовые стратегии компании на примере пивной отрасли¹

Продукция компании «Балтика» ориентирована на максимально широкий круг покупателей, подчеркивая это слоганом «народное пиво России». Компания «Вена», наоборот, инвестировала средства в дифференциацию, когда создаются марки для каждой группы потребителей (Tuborg Gold Label и «Невское»). Компания Guinness применяет для своей марки стратегию концентрации, позиционируется в одном сегменте рынка темного пива, что позволяет компании получать наибольшую норму прибыли за счет уникальности продукта. ^[2]

одель международного обмена (Хекшер — Олин)

В стране производят ткань (х) и хлеб (у) из труда (L) и земли (7), производственные функции заданы формулами (10.11).

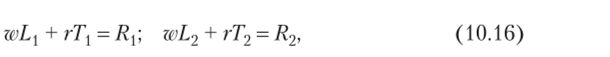
В каждой отрасли суммарная стоимость ресурсов равна фиксированной величине затрат:

где w иг — цены труда и земли; R_i и R₂ — затраты на ресурсы в отраслях. Ограничения для экономики в целом:

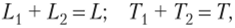
где L и Т — общие объемы труда и земли в стране.

Функция «цены — ресурсы» — зависимость отношения затрат ресурсов в отрасли от отношения их цен при оптимальном выпуске отрасли.

Максимизируем каждый выпуск (10.15) при соответствующем ограничении (10.16), тогда для каждой отрасли относительные затраты земли (Т/ L) прямо пропорциональны относительной цене труда (да / г). Иными словами, функция «цены — ресурсы» есть прямая пропорциональность:

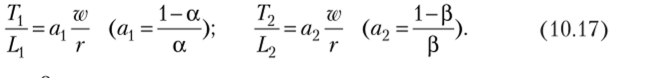
Поскольку а > (3, то а_х < а_ъ а значит, при заданных ценах ресурсов относительные затраты земли меньше при производстве ткани, чем при производстве хлеба. Полученные функции не учитывают цены продуктов и не позволяют рассчитать оптимальное распределение ресурсов между отраслями.

Определим оптимальные затраты ресурсов и цену ткани (р_{) при производстве единицы ткани с учетом кривой «цены — ресурсы», получим систему трех уравнений относительно Т_х, Z._t, р{.

Решение этой системы:

Аналогичную формулу получим для цены хлеба (р₂).

Функция «цены — цены» — зависимость отношения цен продуктов от отношения цен ресурсов при оптимальном выпуске обеих отраслей. Разделив р_х на р_ъ получим функцию «цены — цены» степенного вида:

Поскольку а > р, то из (10.18) следует, что чем дороже труд относительно земли, тем дороже ткань относительно хлеба. Поскольку аир меньше единицы, то и их разность меньше единицы, а поэтому функция «цены — цены» растает замедленным темпом.

Относительные затраты земли в каждой отрасли и относительная цена ткани удовлетворяют соотношениям, задаваемым отраслевыми функциями «цены — ресурсы» (10.17) и функцией «цены — цены» (10.18), т.е. эти показатели являются решением системы трех уравнений. Оптимальные выпуски ткани (.г*) и хлеба (у*) являются функциями относительной цены ткани {р =Р / р₂)-

Функция относительного предложения ткани (RS) — отношение оптимальных выпусков ткани и хлеба:

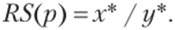
Данная функция задана на некотором промежутке изменения относительной цены ткани и возрастает от нуля до бесконечности.

Объем спроса па каждый товар считаем пропорциональным численности населения и обратно пропорциональным цене товара:

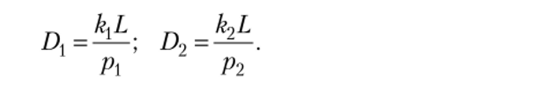
Функция относительного спроса на ткань (RD) — отношение функций спроса на ткань и хлеб. Данная функция убывает с ростом относительной цены ткани:

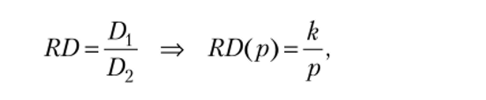
где k = k_x / k₂.

В равновесии относительный спрос равен относительному предложению:

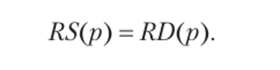
Равновесная цена р* определяет оптимальное отношение цен продуктов и ресурсов и отраслевых затрат ресурсов.

Международный обмен. Имеются две страны, в которых производят ткань и хлеб. Производственные функции и объемы ресурсов одинаковы.

Пусть население второй страны сократилось, тогда первая страна станет трудоизбыточной, а вторая страна — землеизбыточной. Кривая RD не изменится, а кривая RS во второй стране сдвинется вверх. В итоге равновесная относительная цена ткани во второй стране станет больше, а равновесный относительный выпуск ткани станет меньше. Существует множество коэффициентов обмена, выгодных обеим странам. Обмен производится до тех пор, пока относительные цены и относительные объемы выпуска не сравняются в обеих странах: в трудоизбыточной стране цена ткани растет, ее выпуск падает, в землеизбыточной стране цена ткани падает, ее выпуск растет.

Модель глобального равновесия

Обобщим простейшую кейнсианскую модель равновесия на случай глобальной экономики. Аналогом дохода страны (ВВП) здесь служит вектор, состоящий из доходов всех стран, а аналогом предельной склонности к сбережению — матрица, характеризующая норму сбережения в каждой стране и интенсивность экспорта из одной страны в другую.

Интенсивность экспорта из страны i в страну j (я,-,) — это доля, которую составляет экспорт в/-го страну в доходе г-й страны (#,-), причем я„ — это удельный вес внутренних расходов в ее выпуске. Матрица интенсивности экспорта экзогенна: А = {«,?,}. Склонность к потреблению в стране г равна сумме элементов г-й строки матрицы А, эта сумма меньше единицы.

Автономные расходы г-й страны (EJ) экзогенны, они финансируются за счет кредитов и не связаны с внутренним производством или импортом. Совокупные расходы в каждой стране (?)) образуются из автономных расходов, части собственного ВВП и импорта. В случае двух стран система уравнений относительно доходов имеет вид

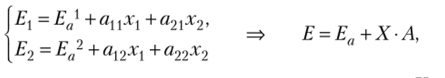
где Е_а и Е — векторы автономных и совокупных расходов; X — вектор доходов.

Матричная функция совокупных расходов является аналогом скалярной функции совокупных расходов в теории Кейнса, причем матрица А выступает аналогом предельной склонности к потреблению. По аналогии с моделью Кейнса определим глобальное равновесие.

Глобальное равновесие — в каждой стране совокупные расходы равны доходу, т.е. вектор доходов равен вектору совокупных расходов:

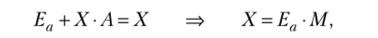
где I — единичная матрица; М = (/ - А) * — глобальный мультипликатор.

Глобальный мультипликатор — матрица, на которую нужно умножить вектор совокупных расходов, чтобы получить вектор равновесных доходов при глобальном равновесии. Он является матрицей, обратной к матрице I - А, и служит аналогом простого мультипликатора т = (1 - МРС) ¹в теории Кейнса и матрицы полных затрат (мультипликатора Леонтьева) в линейной балансовой модели. Выясним экономический смысл глобального мультипликатора. Рассмотрим прирост дохода j-й страны, вызванный инвестиционным импульсом ДI, в г-й стране, при этом инвестиционные импульсы в других странах равны нулю:

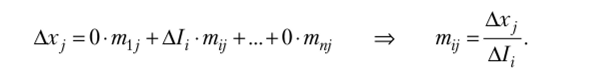
На основании данной формулы определим мультипликаторы скалярного типа.

Перекрестный мультипликатор — прирост дохода в одной стране, порожденный единичным инвестиционным импульсом в другой стране; это элемент матрицы глобального мультипликатора (iW), лежащий вне главной диагонали.

Внутренний мультипликатор страны — прирост дохода в стране, порожденный единичным инвестиционным импульсом в той же стране, это есть элемент матрицы глобального мультипликатора (М), лежащий на главной диагонали.

Внешний мультипликатор в г-й стране (т,) — прирост мирового выпуска, порожденный единичным приростом инвестиций в данной стране, он равен сумме элементов г-й строки матрицы глобального мультипликатора:

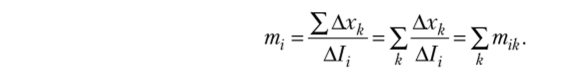
Глобальный скалярный мультипликатор (т) — прирост мирового выпуска, порожденный одновременным действием единичных инвестиционных импульсов во всех странах. Он равен сумме элементов матрицы глобального мультипликатора и характеризует степень глобализации мировой экономики.

Пример

В странах А и В нормы сбережения равны 22% и 27%, доли экспорта в ВВП — 20% и 30%, объемы автономного потребления — 20 и 10. Тогда удельный вес внутреннего использования ВВП в стране

А равен 1 - 0,22 - 0,2 = 0,58, в стране В равен 1 - 0,27 - 0,3 = 0,43, а равновесные доходы равны:

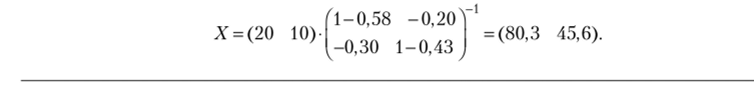
Рассмотрим модель глобального равновесия с налогами. Пусть в каждой стране введен единый налог, которым облагаются экспорт и внутреннее потребление. Тогда совокупные расходы равны

где Т— диагональная матрица, элементами которой служат национальные ставки налогов.

Из условия глобального равновесия следует формула вектора равновесных доходов:

Х = Е_аМ_т,

где М_т- (I - (I - Т) ? Л)^-1 — налоговый глобальный мультипликатор.

Смотрите также файлы

Реферат по История дисциплине Тема Президент Франции во второй половине хх века Николя Саркози.doc

Конвенция Монтевидео о правах и обязанностях государств 1933 г. документ, выделяющий признаки государства.docx

Император ГоЭнью был 4м императором Японии в период с 1371 по 1382 годы. Он был рожден 11 июня 1359 года и был наследником трона в возрасте 12 лет после смерти своего отца Императора Чёрного Вакса.docx

Отчет по стажировке слушателя (фамилия, имя, отчество).rtf

Правоспособность, дееспособность и деликтоспособность субъектов правоотношений.docx

Файл: Тема 1 Макроэкономика ее предмет и методы познания макроэкономических процессов.docx

одель международного обмена (Хекшер — Олин)

Модель глобального равновесия

Смотрите также файлы

Информация

Списки файлов

Дополнительно