Файл: Тике в школе Организация элективного курса по математике для изучения приложений производной.docx
Добавлен: 06.11.2023
Просмотров: 133
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Глава 1. Теоретические основы организации элективных курсов по математике в средней школе
1.1 Сущность понятия «элективный курс», его цели, задачи и функции
1.2. Роль и место элективных курсов по математике в учебном процессе
2.1 Понятие производной и её приложения
2.2. Анализ учебно-методической литературы по теме «Приложения производной»
2.3 Разработка дидактического материала для элективного курса «Производная и её приложения»
2.4. Разработка содержания элективного курса «Производная и её приложения»
, стоит отметить их важнейшую роль в развитии базового курса математики и получении дополнительной подготовки. Помимо этого, они способствуют развитию кругозора и интеллектуальных способностей школьников, способствуют совершенствованию аналитического мышления.
Производная функции – основное понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке [8].
Определяется производная как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует:
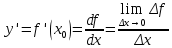
Функцию, имеющую конечную производную, называют дифференцируемой.
Физический смысл производной заключается в том, что, если функция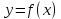 и ее аргумент
и ее аргумент 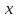 являются физическими величинами, то производная
являются физическими величинами, то производная 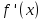 – это скорость изменения величины
– это скорость изменения величины 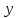 относительно величины
относительно величины 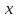 [17].
[17].
Геометрический смысл производной: значение производной функции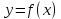 в точке
в точке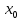 равно угловому коэффициенту касательной к графику этой функции (рисунок 4) в точке
равно угловому коэффициенту касательной к графику этой функции (рисунок 4) в точке 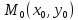 , где
, где 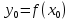 [8].
[8].
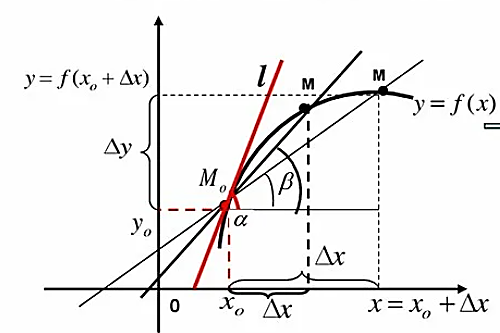
Рисунок 2. Геометрический смысл производнойи функции
На рисунке 3 представлена таблица производных элементарных функций.
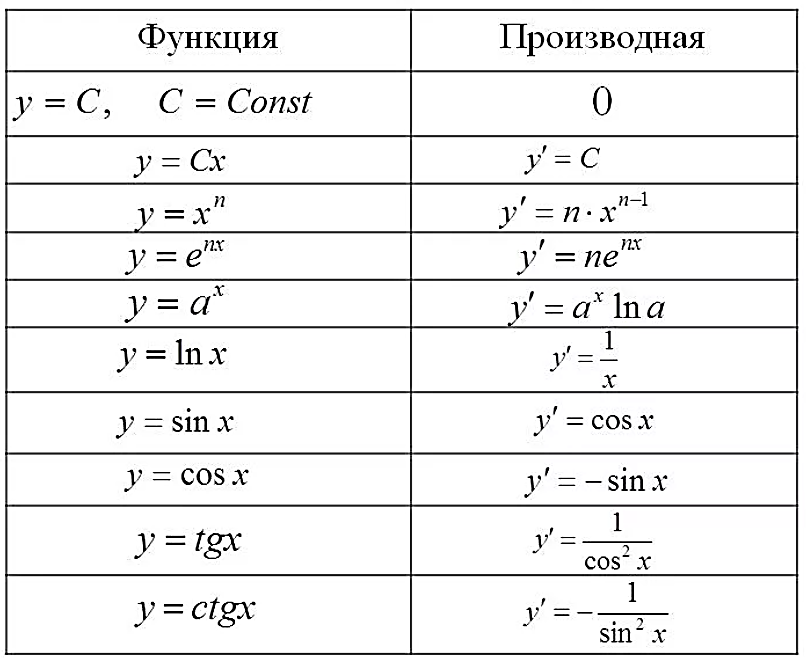
Рисунок 3. Таблица производных
Одним из важнейших приложений дифференциального исчисления является разработка общих методов исследования функции. Производная используется также при решении экстремальных задач, которые сводятся к нахождению наибольших или наименьших значений функции в области её определения. Такие задачи возникают в различных областях знаний, в том числе в физике и экономике. В каждой конкретной задаче, прежде чем приступить к её решению, надо выяснить, существует ли наибольшее или наименьшее значение рассматриваемой функции. Ответ на этот вопрос даёт теорема Карла Вейерштрасса: непрерывная на отрезке функция ограничена и достигает хотя бы раз своего наибольшего или наименьшего значений на этом отрезке. На эту теорему опирается ряд других теорем, которые служат теоретической основой многих приложений производной [23].
Большинство функций на разных промежутках области определения ведут себя по-разному, на одних возрастают, на других убывают. Рассмотрим поведение функции на интервале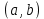 .
.
Так, если для любых двух точек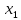 и х2 из интервала
и х2 из интервала 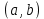 большему значению аргумента соответствует большее значение функции, то есть для
большему значению аргумента соответствует большее значение функции, то есть для 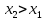 будет
будет 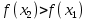 , то функция
, то функция  называется возрастающей на
называется возрастающей на  ; если для
; если для 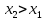 будет
будет 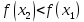 , то функция называется убывающей на
, то функция называется убывающей на 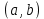 .
.
Функция, которая на интервале только возрастает или только убывает, называется монотонной. Узнать, является ли функция возрастающей или убывающей, можно используя некоторые теоремы. Рассмотрим их.
Теорема 1. Если функция дифференцируема на
дифференцируема на 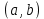 и возрастает, то её первая производная неотрицательна во всех точках этого интервала, то есть
и возрастает, то её первая производная неотрицательна во всех точках этого интервала, то есть 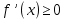 на
на 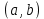 .
.
Теорема 2. Если функция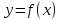 убывает на
убывает на 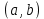 , то
, то 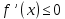 , то есть производная первого порядка неположительна на
, то есть производная первого порядка неположительна на 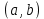 [17].
[17].
Эти теоремы определяют необходимые признаки возрастания и убывания функции на интервале. Для обоснования этих теорем сошлёмся на геометрический смысл производной. Производная функции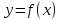 равна угловому коэффициенту касательной к графику функции в каждой её точке, где производная существует. Легко видеть (рисунок 6), что если функция возрастает, то угол наклона касательной острый (в точках А, С) или, в крайнем случае, равен нулю (в точке В), но тангенс острого угла положительный, а угла нулевой величины равен нулю. Таким образом, для возрастающей на
равна угловому коэффициенту касательной к графику функции в каждой её точке, где производная существует. Легко видеть (рисунок 6), что если функция возрастает, то угол наклона касательной острый (в точках А, С) или, в крайнем случае, равен нулю (в точке В), но тангенс острого угла положительный, а угла нулевой величины равен нулю. Таким образом, для возрастающей на
 функции
функции 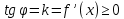 .
.
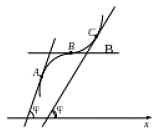
Рисунок 4. График возрастающей функции
Аналогично, если функция дифференцируема на и убывает, то углы наклона касательных к положительному направлению оси абсцисс тупые (или равны нулю) (рисунок 7). Но тангенсы тупых углов отрицательны, а нулевых — равны нулю. Следовательно,
и убывает, то углы наклона касательных к положительному направлению оси абсцисс тупые (или равны нулю) (рисунок 7). Но тангенсы тупых углов отрицательны, а нулевых — равны нулю. Следовательно,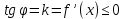 .
.
Рисунок 5. График убывающей функции
Обратные теоремы определяют достаточные признаки возрастания и убывания функции:
Если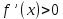 на
на  , то функция
, то функция  возрастает на
возрастает на  .
.
Если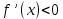 на
на  , то функция
, то функция  убывает на
убывает на  [1].
[1].
Английский физик и математик Исаак Ньютон (1643-1727) отметил, что понятие производной возникло как математическое описание скорости движения. Поэтому важнейшим приложением производной является вычисление скорости. Скорость произвольно движущейся точки является векторной величиной, так как она определяется с помощью вектора – перемещения точки за промежуток времени. Простейший случай — движение точки по прямой. При прямолинейном движении точки ее положение, перемещение, скорость, ускорение и другие характеристики, которые имеют векторный смысл, можно задать числом, то есть считать скалярными величинами. Ускорение произвольного движения определяется как скорость изменения скорости, то есть как производная скорости по времени: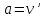 [17].
[17].
Так как скорость есть производная координаты
, а ускорение есть производная скорости, то ускорение называют второй производной координаты и обозначают так: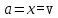 .
.
Через координату точки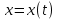 и ее производные можно выразить другие механические величины:
и ее производные можно выразить другие механические величины:
– сила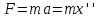 , где m — масса;
, где m — масса;
– импульс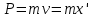 .
.
В математике производные имеют широкое применение. Они используются во многих ситуациях, например: нахождение максимумов или минимумов функции, нахождение угла наклона кривой и точек перегиба. Наиболее распространенное использование применения производных заключается в:
– нахождении скорости изменения величины;
– нахождении значения аппроксимации;
– нахождении уравнения касательной и нормали к кривой;
– нахождении точек максимума, минимума и перегиба;
– определении возрастающих и убывающих функций [10].
Производную функции можно применить там, где есть неравномерное протекание процесса: переменный ток, радиоактивный распад и другие химические реакции, неравномерное механическое движение и другие [38]. Например, в таких областях:
Глава 2. Методические аспекты организации элективного курса по математике для изучения приложений производной
2.1 Понятие производной и её приложения
Производная функции – основное понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке [8].
Определяется производная как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует:
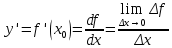
Функцию, имеющую конечную производную, называют дифференцируемой.
Физический смысл производной заключается в том, что, если функция
 и ее аргумент
и ее аргумент  являются физическими величинами, то производная
являются физическими величинами, то производная 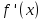 – это скорость изменения величины
– это скорость изменения величины 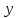 относительно величины
относительно величины 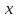 [17].
[17].Геометрический смысл производной: значение производной функции
 в точке
в точке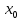 равно угловому коэффициенту касательной к графику этой функции (рисунок 4) в точке
равно угловому коэффициенту касательной к графику этой функции (рисунок 4) в точке 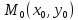 , где
, где 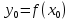 [8].
[8].
Рисунок 2. Геометрический смысл производнойи функции
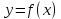
На рисунке 3 представлена таблица производных элементарных функций.

Рисунок 3. Таблица производных
Одним из важнейших приложений дифференциального исчисления является разработка общих методов исследования функции. Производная используется также при решении экстремальных задач, которые сводятся к нахождению наибольших или наименьших значений функции в области её определения. Такие задачи возникают в различных областях знаний, в том числе в физике и экономике. В каждой конкретной задаче, прежде чем приступить к её решению, надо выяснить, существует ли наибольшее или наименьшее значение рассматриваемой функции. Ответ на этот вопрос даёт теорема Карла Вейерштрасса: непрерывная на отрезке функция ограничена и достигает хотя бы раз своего наибольшего или наименьшего значений на этом отрезке. На эту теорему опирается ряд других теорем, которые служат теоретической основой многих приложений производной [23].
Большинство функций на разных промежутках области определения ведут себя по-разному, на одних возрастают, на других убывают. Рассмотрим поведение функции на интервале
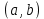 .
.Так, если для любых двух точек
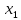 и х2 из интервала
и х2 из интервала 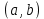 большему значению аргумента соответствует большее значение функции, то есть для
большему значению аргумента соответствует большее значение функции, то есть для 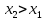 будет
будет 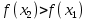 , то функция
, то функция  называется возрастающей на
называется возрастающей на 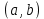 ; если для
; если для 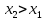 будет
будет 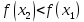 , то функция называется убывающей на
, то функция называется убывающей на 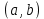 .
. Функция, которая на интервале только возрастает или только убывает, называется монотонной. Узнать, является ли функция возрастающей или убывающей, можно используя некоторые теоремы. Рассмотрим их.
Теорема 1. Если функция
 дифференцируема на
дифференцируема на 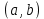 и возрастает, то её первая производная неотрицательна во всех точках этого интервала, то есть
и возрастает, то её первая производная неотрицательна во всех точках этого интервала, то есть 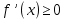 на
на 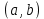 .
.Теорема 2. Если функция
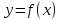 убывает на
убывает на 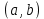 , то
, то 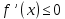 , то есть производная первого порядка неположительна на
, то есть производная первого порядка неположительна на 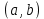 [17].
[17].Эти теоремы определяют необходимые признаки возрастания и убывания функции на интервале. Для обоснования этих теорем сошлёмся на геометрический смысл производной. Производная функции
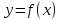 равна угловому коэффициенту касательной к графику функции в каждой её точке, где производная существует. Легко видеть (рисунок 6), что если функция возрастает, то угол наклона касательной острый (в точках А, С) или, в крайнем случае, равен нулю (в точке В), но тангенс острого угла положительный, а угла нулевой величины равен нулю. Таким образом, для возрастающей на
равна угловому коэффициенту касательной к графику функции в каждой её точке, где производная существует. Легко видеть (рисунок 6), что если функция возрастает, то угол наклона касательной острый (в точках А, С) или, в крайнем случае, равен нулю (в точке В), но тангенс острого угла положительный, а угла нулевой величины равен нулю. Таким образом, для возрастающей на
 функции
функции 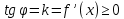 .
.
Рисунок 4. График возрастающей функции
Аналогично, если функция дифференцируема на
 и убывает, то углы наклона касательных к положительному направлению оси абсцисс тупые (или равны нулю) (рисунок 7). Но тангенсы тупых углов отрицательны, а нулевых — равны нулю. Следовательно,
и убывает, то углы наклона касательных к положительному направлению оси абсцисс тупые (или равны нулю) (рисунок 7). Но тангенсы тупых углов отрицательны, а нулевых — равны нулю. Следовательно,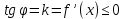 .
.
Рисунок 5. График убывающей функции
Обратные теоремы определяют достаточные признаки возрастания и убывания функции:
Если
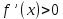 на
на  , то функция
, то функция  возрастает на
возрастает на  .
.Если
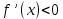 на
на  , то функция
, то функция  убывает на
убывает на  [1].
[1].Английский физик и математик Исаак Ньютон (1643-1727) отметил, что понятие производной возникло как математическое описание скорости движения. Поэтому важнейшим приложением производной является вычисление скорости. Скорость произвольно движущейся точки является векторной величиной, так как она определяется с помощью вектора – перемещения точки за промежуток времени. Простейший случай — движение точки по прямой. При прямолинейном движении точки ее положение, перемещение, скорость, ускорение и другие характеристики, которые имеют векторный смысл, можно задать числом, то есть считать скалярными величинами. Ускорение произвольного движения определяется как скорость изменения скорости, то есть как производная скорости по времени:
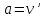 [17].
[17].Так как скорость есть производная координаты
, а ускорение есть производная скорости, то ускорение называют второй производной координаты и обозначают так:
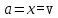 .
.Через координату точки
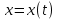 и ее производные можно выразить другие механические величины:
и ее производные можно выразить другие механические величины:– сила
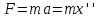 , где m — масса;
, где m — масса;– импульс
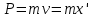 .
.В математике производные имеют широкое применение. Они используются во многих ситуациях, например: нахождение максимумов или минимумов функции, нахождение угла наклона кривой и точек перегиба. Наиболее распространенное использование применения производных заключается в:
– нахождении скорости изменения величины;
– нахождении значения аппроксимации;
– нахождении уравнения касательной и нормали к кривой;
– нахождении точек максимума, минимума и перегиба;
– определении возрастающих и убывающих функций [10].
Производную функции можно применить там, где есть неравномерное протекание процесса: переменный ток, радиоактивный распад и другие химические реакции, неравномерное механическое движение и другие [38]. Например, в таких областях:
-
В физике: при решении задач на скорость движения материальной точки в некоторый момент времени, а также для вычисления наибольшего и наименьшего значения какой-либо величины; -
В химии: для построения математических моделей химических реакций, для описания их свойств. Скорость реакции выражают производной по времени концентрации реагирующих веществ, так как она непрерывно изменяется в ходе процесса; -
В экономике: для нахождения производительности труда, максимальной выпуска и прибыли, минимальных издержек. Каждый из этих показателей представляет функцию от одной или нескольких переменных, нахождение которых сводится к нахождению производной.