Файл: Тике в школе Организация элективного курса по математике для изучения приложений производной.docx

2.2. Анализ учебно-методической литературы по теме «Приложения производной»

Проведем исследование учебников по математике разных авторов на тему «Приложения производной».

1. Алимов Ш.А. «Алгебра и начала математического анализа»: в этом учебнике с целью представления приложений производной (глава 8) применяются термины из физики, а также из техники. В частности, скорость механического движения рассчитывается в виде предела соотношения перемещения к бесконечно малой длине времени. Изучение определения производной автор начинает с классической геометрической модели, однако заостряет внимание на использовании производной в физических, а также в технических задачах. В главе 9 детально разбирается порядок исследования простых функций, построения графиков таких функций. Для расширенного уровня предоставляется точное понятие непрерывности функции, понятие, а также построение асимптот и изучаются вторые производные.

2. Рассмотрим учебник «Алгебра и начала математического анализа», А.Н. Колмогорова. Понятие производной вводится при помощи физического смысла производной – в качестве мгновенной скорости точки в конкретный промежуток времени, а после предлагается математическое понятие в качестве предела разностного отношения. Рассматриваются все базовые элементарные функции, а также большое внимание уделяется геометрическому значению производной. В главе 3 представлено использование производной к исследованию функций, добавляется определение второй производной. Представление учебной информации учитывает разный уровень подготовки школьников. Но в учебном пособии слабо выражено приложение производной к задачам по геометрии, по физике, а также по технике. Практические задачи также учитывают уровневую дифференциацию.

3. Рассмотрим учебник «Алгебра и начала математического анализа» А.Г. Мордковича. Достаточно детально разобраны вопросы производной, по технике дифференцирования, включая логарифмические и показательные функции. Большое внимание уделено вопросам: построения касательных, поиска экстремумов, анализа графиков функций. На данные разделы предлагается потратить больше половины от общего объема часов программы по алгебре. В учебниках есть задачи различной сложности, начиная с элементарных и заканчивая задачами высокого уровня сложности.

---

Говоря об иностранных учебных материалах, заметим, что, различаясь темами высшей математики, методика рассмотрения раздела производной в источниках других стран не имеет значительных различий от методики, которая используется в России.

Проблемы, которые появляются в процессе изучения производной и её приложений, возникают из-за многообразия приёмов, применяемых с целью выполнения задач разделов, они существенно обширнее, чем приёмы, которые имеются в большей части учебных пособий.

В ходе анализа содержания школьных учебников по теме «Производная» выявлены характерные черты методики введения производной:

– последовательность изложения материала;

– количество средств наглядности;

– наличие задач на геометрический смысл производной;

– наличие задач прикладного содержания и их характер.

2.3 Разработка дидактического материала для элективного курса «Производная и её приложения»

Приведём примеры заданий для обучающихся 10-11 классов по теме «Производная и её приложения», которые можно использовать на занятиях элективного курса.

Тема 1. Понятие производной. Правила дифференцирования.

Задание № 1. Соотнесите функцию с ее производной (таблица 2).

Таблица 2

1.	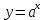а)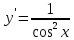
2.	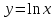б)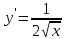
3.	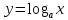в)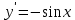
4.	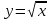г)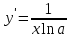
5.	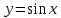д)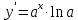
6.	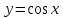е)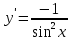
7.	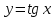ж)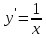
8.	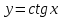з)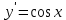

---

Ответ: 1 – д, 2 – ж, 3 – г, 4 – б, 5 – з, 6 – в, 7 – а, 8 – е.

Задание № 2. Вставьте в предложения пропущенные слова:

1. Если производная в точке меняет знак с «+» на «-», то эта точка называется точкой ____________ функции.

2. Если производная в точке меняет знак с «-» на «+», то эта точка называется точкой ______________ функции.

3. Если производная функции положительна на заданном интервале, то функция _____________ на этом интервале.

4. Если производная функции отрицательна на заданном интервале, то функция ____________ на этом интервале.

Ответ: 1 – максимума, 2 – минимума, 3 – возрастает, 4 – убывает.

Задание №3. По графику функции (рисунок 8) найдите производную в точке :



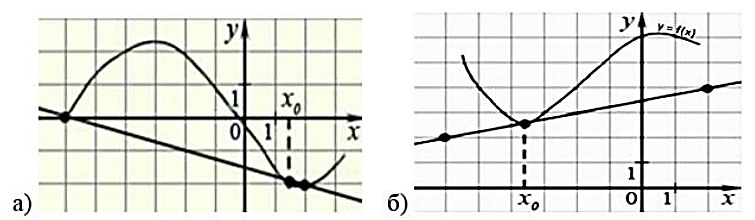
Рисунок 8

Ответ: а) -0,25; б) 0,25.

Задание №4. Решите кроссворд:

1. Если существует … отношения приращения функции к приращению функции при стремлении приращения аргумента к нулю, то говорят, то функция дифференцируема.

2. Как называется точка, в которой производная равна 0 или не существует?

3. Величина, определяемая как производная скорости по времени.

4. Как называется операция отыскания производной?

5. … смысл производной выражает скорость изменения процесса в момент времени t.

6. Положительная вторая производная характеризует … функции.

7. Ученый, пришедший к понятию производной, исходя из вопросов механики.

8. При помощи какого предмета итальянский математик Тарталья изучал угол наклона касательной?

9. Немецкий математик, один из основателей дифференциального исчисления.

10. «Прямая наиболее тесно примыкающая к кривой в малой окрестности заданной точки». О чем писал Ферма?

11. Производная координаты по …, есть скорость (в именительном падеже).

Ответы на рисунке 9.



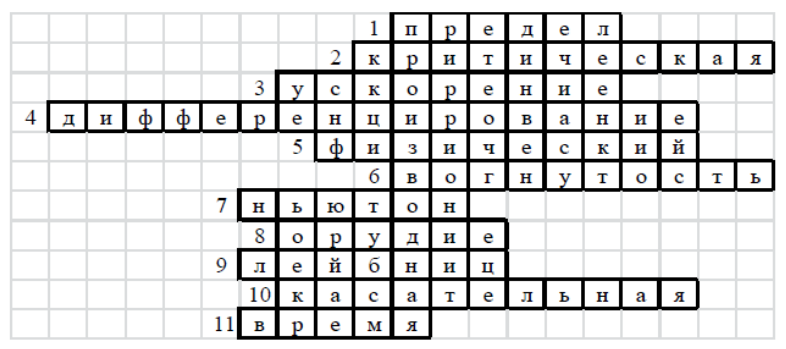
Рисунок 9. Кроссворд

Тема 2. Производная и ее применение в алгебре.

Задача № 1. Доказать тождество .

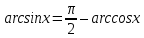Решение. Рассмотрим функцию 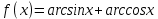. Она определена на отрезке [-1;1]. Найдём производную этой функции: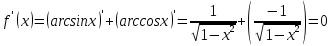

---

Так как производная равна нулю для всех возможных значений аргумента, кроме концов рассматриваемого отрезка, следовательно, функция 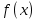является постоянной на этом отрезке. Найдём значение этой функции при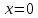



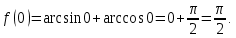
Значит, 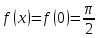. Тождество доказано.

Задача № 2. К графику функции 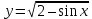проведена касательная в точке с абсциссой 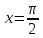. Найдите угловой коэффициент касательной.

Решение. Воспользуемся геометрическим смыслом производной для нахождения углового коэффициента касательной, так как угловой коэффициент касательной, проведенной к графику функции в этой точке, равен производной от этой функции в данной точке. Тогда





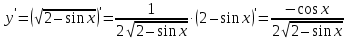
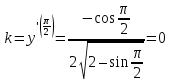
Ответ: 0.

Задача № 3. Найдите экстремумы функции .

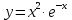Решение.

Областью определения функции является множество всех действительных чисел: .

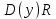Найдём производную функции и ее критические точки:



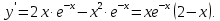
Производная равна нулю, ес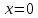ли или 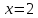. Точек, в которых производная не существует, нет.

Определяем знак производной на каждом из интервалов, на которые критическими точками разбита область определения функции (рисунок 10):



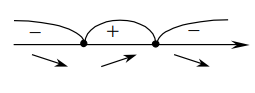
Рисунок 10

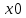– точка минимума функции 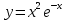, так при переходе через эту точку производная меняет знак с «–» на «+».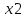

---

– точка максимума функции , так при переходе через эту точку производная меняет знак с «+» на «–».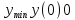

,

.

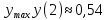Ответ: , .

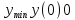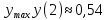Задача № 5. Решите уравнение



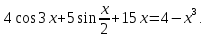
Решение. Рассмотрим функцию, стоящую в левой части заданного уравнения: 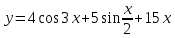. Найдём её производную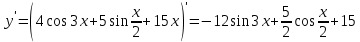



Производная положительна при всех действительных значениях аргумента, следовательно, функция возрастает на всей числовой прямой.

Рассмотрим функцию, стоящую в правой части заданного уравнения: 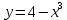. Найдём её производную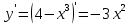



Производная неположительна при всех действительных значениях аргумента, следовательно, функция убывает на всей числовой прямой.

На основании утверждения «о встречной монотонности» можно сделать вывод, что уравнение имеет единственный корень. Подстановкой убеждаемся, что этим корнем является .

Ответ: .

Тема 3. Производная и ее применение в физике.

Задача № 1. Найдите скорость и ускорение материальной точки в момент времени 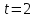, если материальная точка движется прямолинейно по следующему закону .

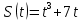Решение. Вычисляем первую производную пути по времени для нахождения скорости:



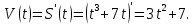
Найдем скорость в момент времени .



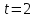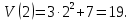
Вычисляем вторую производную пути по времени для нахождения ускорения:

---