Файл: 1 Определение линейного пространства. Следствия из аксиом. Линейное пространство.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 123
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 был оператором простой структуры, необходимо и достаточно, чтобы для любого его собственного числа
был оператором простой структуры, необходимо и достаточно, чтобы для любого его собственного числа  имело место равенство
имело место равенство 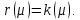
35) Инвариантные подпространства. Индуцированный оператор
Опр. Подпространство P линейного пространства L называется инвариантным относительно линейного оператора
 , если для любого вектора
, если для любого вектора 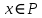 его образ
его образ 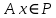
Для любого линейного оператора существует по крайней мере два инвариантных подпространства – нулевое подпространство и все пространство
 Они называются тривиальными.
Они называются тривиальными.Теорема: Инвариантными подпространствами линейного оператора A являются его ядро, образ и произвольное собственное подпространство.
Теорема: Сумма и пересечение инвариантных подпространств являются инвариантными подпространствами
Пусть P подпространство размерности k, инвариантное относительно линейного оператора A. Тогда существует такое подпространство Q, которое будет прямым дополнением пространства P, то есть L=P+Q
Пусть
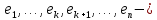 базис пространства
базис пространства  где
где 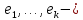 базис
базис 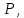 а
а 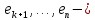 базис
базис 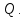
Подействуем на базисные вектора линейным оператором и полученные образы разложим по тому же базису
A
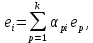
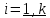
A
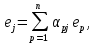
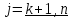
Матрица линейного оператора будет ступенчатая
Если подпространство Q тоже инвариантно, тогда матрица оператора будет блочно-диагональная
Опр. Оператор A, определенный только для векторов некоторого инвариантного подпространства, будем называть индуцированным на этом подпространстве.
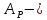 индуцированный оператор на подпространстве
индуцированный оператор на подпространстве  A
A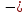 порождающий оператор.
порождающий оператор.Пусть
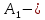 матрица индуцированного оператора
матрица индуцированного оператора 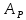 в базисе
в базисе 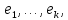
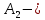 матрица индуцированного оператора
матрица индуцированного оператора 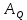 в базисе
в базисе 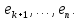
Теорема: Характеристический многочлен порождающего оператора равен произведению характеристических многочленов соответствующих индуцированных операторов
36) Минимальный многочлен вектора и пространства
Опр. Ненулевой многочлен f(t) будем называть аннулирующим многочленом для вектора
 , если f(A)x=0
, если f(A)x=0Свойства
-
Аннулирующий многочлен любого вектора существует -
Сумма и разность аннулирующих многочленов вектора есть аннулирующий многочлен этого вектора -
Произведение анн. мн. на произвольный мн. есть анн. мн. -
НОД двух анн. мн. есть анн. мн. (Это следует из Т. о линейном представлении НОД)
Опр. Ненулевой многочлен
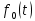 будем называть минимальным аннулирующим многочленом для вектора
будем называть минимальным аннулирующим многочленом для вектора 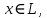 если
если-
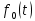 является аннулирующим многочленом
является аннулирующим многочленом -
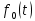 является приведенным многочленом
является приведенным многочленом -
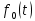 имеет наименьшую степень среди всех анн. мн. вектора
имеет наименьшую степень среди всех анн. мн. вектора
Теорема: Для того, чтобы многочлен f(t) был анн. мн. вектора, необходимо и достаточно, чтобы он делился на min анн. мн. этого вектора
Теорема: Min мн. вектора определяется единственным образом
Алгоритм построения min мн. вектора
Опишем алгоритм построения минимального многочлена вектора. Пусть
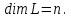 Составляем ряд векторов
Составляем ряд векторов 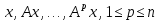 до тех пор, пока
до тех пор, пока 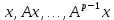 линейно независимы, а
линейно независимы, а 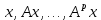 уже линейно зависимы.
уже линейно зависимы.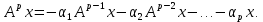
Многочлен
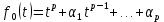 будет минимальным многочленом вектора
будет минимальным многочленом вектора  .
.Опр. Ненулевой многочлен F(t) будем называть аннулирующим многочленом для пространства L, если F(A)x=0 для любого вектора
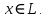
Свойства такие же
Опр. Ненулевой многочлен
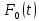 называть минимальным аннулирующим многочленом пространства L, если
называть минимальным аннулирующим многочленом пространства L, если-
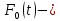 аннулирующий многочлен пространства
аннулирующий многочлен пространства -
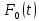 является приведенным многочленом
является приведенным многочленом -
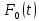 имеет наименьшую степень среди всех аннулирующих многочленов пространства.
имеет наименьшую степень среди всех аннулирующих многочленов пространства.
Теорема: Для того, чтобы многочлен f(t) был анн. мн. пространства, необходимо и достаточно, чтобы он делился на min анн. мн. этого пространства
Алгоритм построения min мн. пространства
Выберем в
 базис
базис  Для каждого базисного вектора
Для каждого базисного вектора 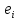 построим его минимальный многочлен
построим его минимальный многочлен 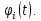
Пусть
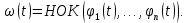
Для любого вектора

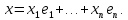
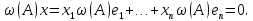
Следовательно,
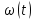 является аннулирующим многочленом пространства
является аннулирующим многочленом пространства 
Нетрудно видеть, что это многочлен наименьшей степени, т.е. минимальный многочлен.
37) Относительный и минимальный многочлен вектора и пространства
Пусть P - инвариантное относительно лин. оператора. A подпространство в L
Опр. Ненулевой многочлен p(t) называется аннулирующим многочленом для вектора
 относительно подпространства P, если
относительно подпространства P, если 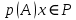
Свойства такие же
Опр. Ненулевой приведенный многочлен
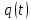 называется минимальным аннулирующим многочленом для вектора
называется минимальным аннулирующим многочленом для вектора  относительно подпространства
относительно подпространства  если
если-
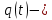 относительный аннулирующий многочлен
относительный аннулирующий многочлен -
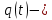 относительный аннулирующий многочлен минимальной степени.
относительный аннулирующий многочлен минимальной степени.
Теорема: Для того, чтобы многочлен p
 был относительным аннулирующим многочленом вектора, необходимо и достаточно, чтобы он делился на относительный минимальный многочлен этого вектора.
был относительным аннулирующим многочленом вектора, необходимо и достаточно, чтобы он делился на относительный минимальный многочлен этого вектора.Следствие: Относительный минимальный многочлен является делителем абсолютного минимального многочлена.
Теорема: Относительный минимальный многочлен вектора определяется единственным образом.
Теорема: Относительные минимальные многочлены сравнимых по модулю
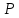 векторов совпадают.
векторов совпадают.Опишем алгоритм построения относительного минимального многочлена.
Пусть
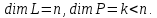
Рассмотрим линейные подпространства