Файл: ХантыМансийский автономный округЮгра Муниципальное образование город Нижневартовск Муниципальная общеобразовательная средняя школа 21 Педагогический проект.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 52
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Проведённые мною исследования показывают, что уровень мотивации обучающихся к предмету возрастает.
Вместе с тем отмечается положительное влияние работы с одарёнными детьми на повышение общего интереса к математике. Это обусловлено прежде всего эффективным созданием организационных условий для развития склонностей и способностей, постоянным совершенствованием методической системы; внедрением новых технологий (проблемного обучения, обучения в «малых группах», проектного обучения, ИКТ, дистанционного обучения) на уроках и во внеурочной деятельности.
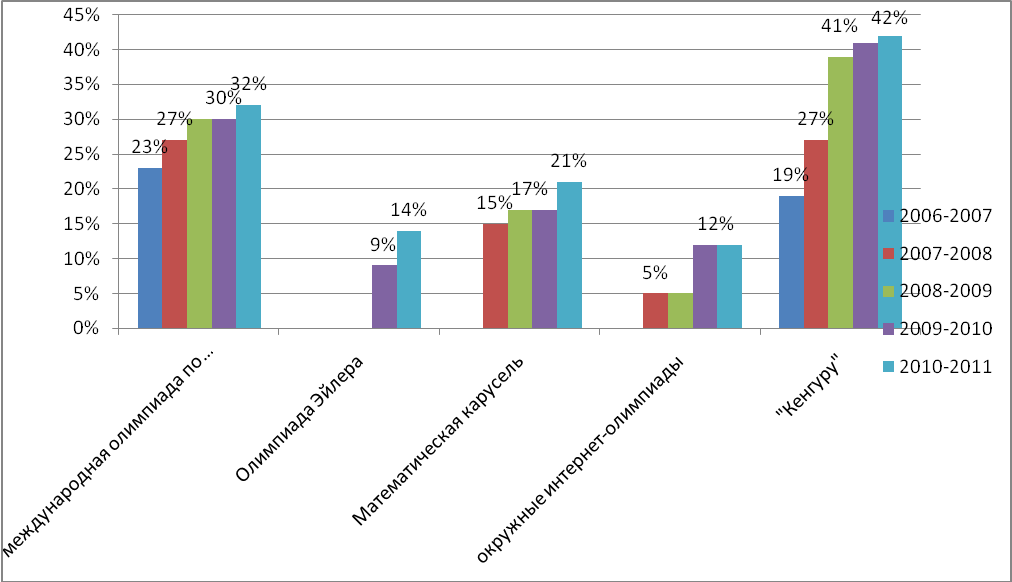
Мои ученики активно посещают кружок по математике, участвуют в математических КВН, брейн-рингах, в международном конкурсе «Кенгуру», в школьных олимпиадах, в олимпиаде по математике Уральского федерального округа, дистанционных олимпиадах, в школьном и городском Слётах научных обществ.
В каждом выпуске имею призеров Всероссийской олимпиады школьников: 2003 год- 3 место в муниципальном этапе (Талмач Михаил), 2009 - 2 место (Корнилов Вадим).
В 2007 году оргкомитет Международной математической игры «Кенгуру» по городу Нижневартовску вручил мне грамоту за массовое вовлечение обучающихся в олимпиадное движение.
Достижения в интеллектуальных конкурсах, олимпиадах.
Всероссийская олимпиада школьников.
| Год | Класс | Место в школе | % выполнения работы | Место в городе | % выполнения работы |
| 2016-2017 | 7 класс | 1 место | 82% (Приказ ДО №548 от 20.10.16 г.) | 6 место | 66% (Приказ ДО №597 от 15.11.2016) |
| 2017-2018 | 8 класс | 1 место | 87% (Приказ ДО 2017г.) | 4 место | 51,43% (Приказ ДО г. Нижневартовска от 25.11.2017) |
| 2020-2021 | 6 класс | 1 место | 68,57% (Приказ ДО 2020 г.) | На уровне города не проводится | |
Международная Олимпиада по основам наук УРФО.
| Год | Класс | результат | Примечание |
| 2016-2017 | 7 класс | 7 дипломов 1 степени | Второй этап |
| 3 диплома 3 степени | Финальный (очный) этап | ||
| 2017-2018 | 8 класс | 4 диплома 1 степени | Второй этап |
| 3 диплома 3 степени | Финальный (очный) этап | ||
| 2018-2019 | 9 класс | 3 диплома 1 степени | Первый этап |
Таблица 2. Достижения в дистанционных олимпиадах.
Всероссийский математический конкурс «Отличник».
| Год | Класс | результат | Количество |
| 2016-2017 | 7 класс | Диплом победителя | 3 |
Всероссийский математический конкурс «Кенгуру».
| Год | Класс | результат | Количество участников |
| 2016-2017 | 7 класс | 1 место по школе 5 место по городу | 3 |
| 2017-2018 | 8 класс | 1 место по школе | 7 |
| 2018-2019 | 9 класс | 1 место по школе | 7 |
Онлайн - олимпиада «Я люблю математику».
| Год | Класс | результат | Количество |
| 2020-2021 | 6 класс | Диплом победителя | 6 |
| Диплом призера | 8 |
Высокий уровень учебной мотивации, нацеленность на предмет, высокий уровень математической подготовки являются факторами, определяющими пути получения образования выпускниками после окончания основной школы: 100 % выпускников (из числа обучающихся в 10 классах) изучают математику на профильном уровне. Администрация нашей школы имеет благодарность от лицея города Ханты-Мансийска за качественную подготовку одарённых детей по математике и информатике.
Качественный уровень подготовки за курс основной школы помогает этим ребятам получить высокие баллы на ЕГЭ.
Участвую в работе методического объединения преподавателей математики и информатики школы. Опыт работы по проблемам реализации личностно – ориентированного подхода в преподавании математики, использование метода проектов в работе с одарёнными детьми, применение информационно-коммуникативных технологий при обучении решению текстовых задач по математике, обобщался на уровне педагогического коллектива школы.
Делюсь опытом работы с другими общеобразовательными учреждениями города. В рамках реализации программы сотрудничества «Партнерство – основа успешного развития» организовала семинар по теме «Организация работы с одаренными детьми».
Литература
-
Ведерникова Т.Н. , Иванов О.А. Интеллектуальное развитие школьников на уроках математики // Математика в школе - №3-2002. -
Клюсова В.В.: «Концепция проектирования методики обучения математике в условиях инновационной педагогической системы» -
Панютина Н.И., В.Н. Рагинская, Е.Б. Кислякова, З.Г. Дубровина, Н.А. Коляда и др. Система работы образовательного учреждения с одарёнными детьми. Волгоград. 2008 год. -
Е.И. Щеблакова. Психологическая диагностика одарённости школьниковы: проблемы, методы, результаты исследований и практики. Москва-Воронеж, 2004 год. -
Гайбуллаев Н.Р. Развитие математических способностей учащихся: метод. пособие для учителей. – Ташкент: Укитувчи, 1988. -
Гингулис Э.Ж. Развитие математических способностей учащихся. //Математика в школе. – 1990 - №1. -
Гусев В.А. Психолого-педагогические основы обучения математике. М.: Вербум: Академия, 2003. -
Заиграев А.С. Психология математических способностей. - http://it-med.ru/index.php. -
Колмогоров А.Н. Математика - наука и профессия. М., 1988. -
Кордемский Б.Л. Очерки о математических задачах на смекалку. – М.:Учпедгиз, 1958. -
Крутецкий В. А. Психология математических способностей школьников. М.: Просвещение, 1968. -
Литвинский П.А. Условия развития математических талантов. //Народное образование. – 1992 - №9/10. -
Метельский Н.В. Пути совершенствования обучения математике. – Минск: Университетское, 1989. -
Миракова Т.Н. Развивающие задачи на уроках математики в V-VIII классах: пособие для учителей. – Львов: “Квантор”, 1991. -
Окунев А.А. Спасибо за урок, дети!: ..о развитии творческих способностей учащихся: Книга для учителя: Из опыта работы. – М.: Просвещение, 1988. -
Рубинштейн С.Л. Основы общей психологии. – М., 1989. -
Рубинштейн С.Л. Проблемы общей психологии. – М.: Педагогика, 1976. -
Салюкова С.В. Влияние системы заданий по математике на развитие математических способностей учащихся 7-9 классов. - http://www.bank.orenipk.ru/Text/t29_28.htm. -
Сапожников В.М. Внешние и внутренние условия развития математических способностей. - http://www.mironych.ru/3/2.htm -
Шадриков В.Д. О структуре познавательных способностей. //Психологический журнал – 1985 - №3. -
Юркевич В.С. А. Н. Колмогоров и проблема развития математической одаренности. //Вопросы психологии – 2001 - № 3. -
Якиманская И.С. Психологические основы математического образования: Учеб. Пособие для студ. пед. вузов. – М.:Издательский центр “Академия”, 2004. -
Математика//Еженедельное приложение к газете «Первое сентября».2009. -
Журнал. Профильная школа. 2009-2011 год. -
Беляева Н., Савенков А. И. Одаренные дети в обычной школе // Народное образование. – 1999.– № 9. -
Давыдова Г. А. Дорога в будущее. О современных теориях креативности и одаренности // Психологический журнал. – 1999.- № 3. -
Матюшкин А. М. Концепции творческой одаренности // Вопросы психологии – 1989.–№ 6 .
Приложение 1
Участие обучающихся в проектной и исследовательской деятельности
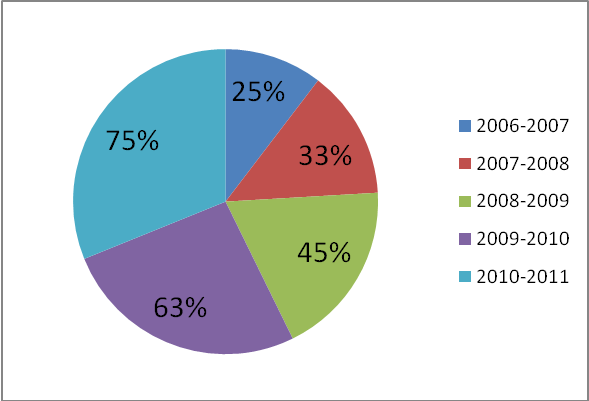
Приложение 2
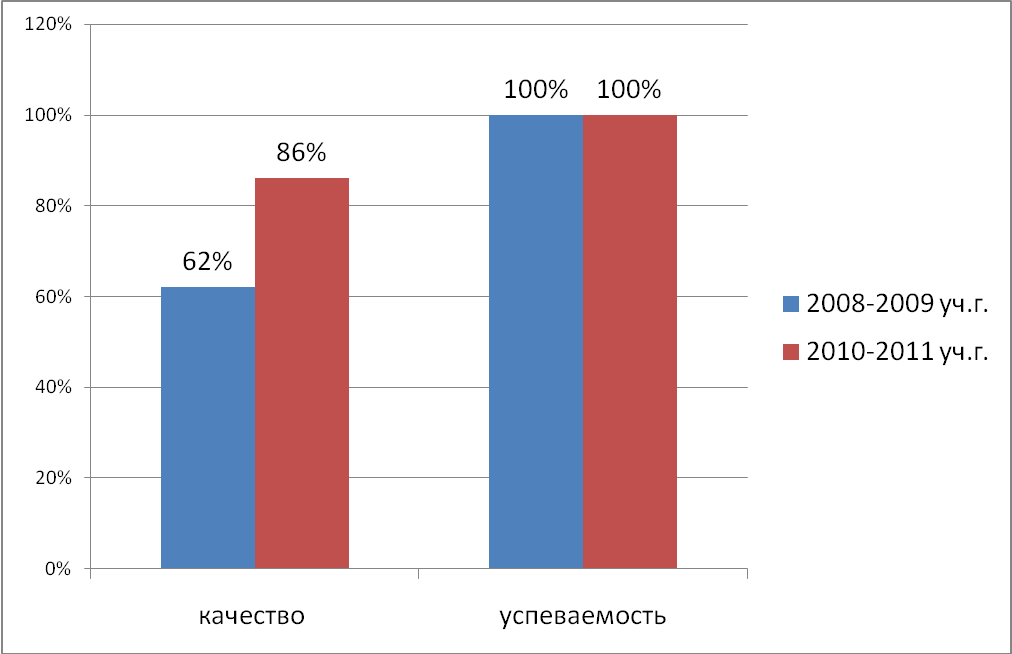
Качество знаний по математике и алгебре при 100% успеваемости
Результаты ГИА (9 класс, новая форма)
Результаты ЕГЭ
| Год | Успеваемость | Качество |
| 2004 | 100% | 62% |
| 2005 | 100% | 63% |
Приложение 3
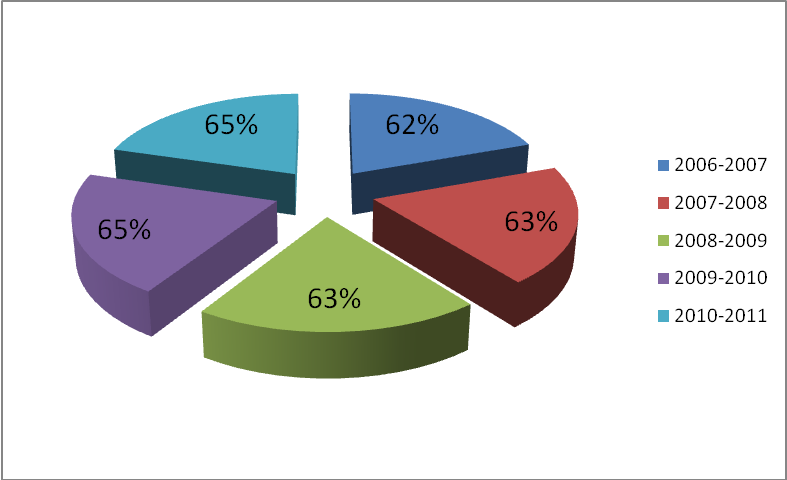
Охват учащихся олимпиадным движением
Приложение 4
Уровень мотивации учащихся 5- 9 классов по математике
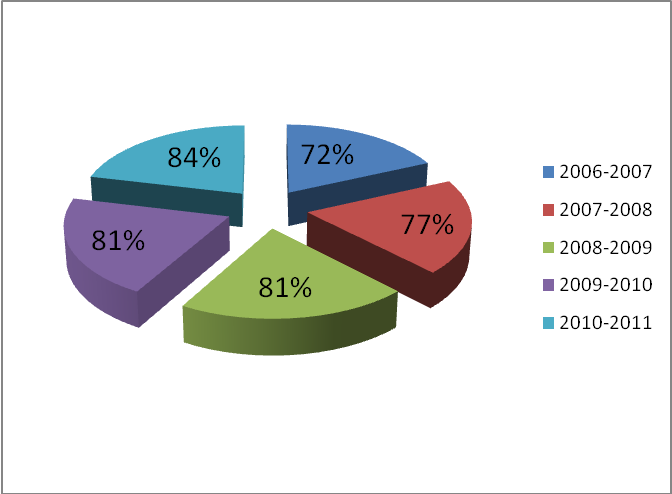
Приложение 5
Система заданий для учащихся 7-9 классов по углублению школьного курса математики
7 КЛАСС
1. Верно ли, что для любых чисел a и b выполняются условия
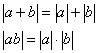
2. Известно, что
3. Известно, что
4. При каких значениях коэффициента m уравнение mx=5 имеет единственный корень? Существует ли такое значение m, при котором это уравнение не имеет корней? Имеет бесконечно много корней?
5. Решите уравнения:
а) (х+2)(х-9) = 0
б) (х+1)(х-1)(х-5) = 0
6. Не решая уравнения 7(2х+1)=13 докажите, что его корень не является целым числом.
7. При каких значениях а уравнение ах = 8 имеет а) корень, равный -4; б) не имеет корней; в) имеет отрицательный корень.
8. При каком значении а точка А (а; -1) принадлежит графику функции у=3,5х
9. Задайте формулой линейную функцию, графиком которой служит прямая, проходящая через точку А(2;3) и параллельная графику функции у=1,5x - 3
10. Докажите, что уравнение